2011中考数学二模整套试题及答案 6页

‎2011中考数学二模整套试题及答案 考生须知 ‎1．本试卷共6页，共五道大题，25道小题，满分120分。考试时间120分钟。‎ ‎2．在试卷和答题纸上认真填写学校名称、班级和姓名。‎ ‎3．试题答案一律填涂或书写在答题纸上，在试卷上作答无效。‎ ‎4．在答题纸上，作图题用2B铅笔作答，其他试题用黑色字迹签字笔作答。‎ ‎5．考试结束，请将本试卷、答题纸和草稿纸一并交回。‎ 一、选择题（本题共32分，每小题4分）‎ 下面各题均有四个选项，其中只有一个是符合题意的. ‎ ‎1．16 的算术平方根是 A． B． C． D． ‎ ‎2. 如果一个角等于，那么它的补角等于 A． B． C． D．‎ ‎3．若点与点关于轴对称，则的值分别是 A． B． C． D． ‎ ‎4. 把多项式分解因式，结果正确的是 A． B． C． D．‎ ‎5. 下列计算正确的是 A． B． C． D． ‎ ‎6．从1～9这九个自然数中任取一个，是3的倍数的概率是 ‎ A． B． C． D． ‎ ‎7．如图是一个几何体的三视图，已知正视图和左视图都是边长为2的等边三角形，则这个几何体的全面积为 ‎ A．　　　　　　B． 　　　　 C． 　　　　 D．‎ ‎8．如图，正方形的边长是3cm，一个边长为1cm的小正方形沿着正方形的边连续翻转（小正方形起始位置在边上），那么这个小正方形翻转到边的终点位置时，它的方向是 ‎ ‎ ‎ A． B． C． D． ‎ 二、填空题（本题共16分, 每小题4分）‎ ‎9. 若分式的值为零 , 则 .‎ ‎10．某中学的一个数学兴趣小组在本校学生中开展主题为“垃圾分类知多少”的专题调查活动，采取随机抽样的方法进行问卷调查，问卷调查的结果划分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级，划分等级后的数据整理如下表：‎ 等级 非常了解 比较了解 基本了解 不太了解 频数 ‎40‎ ‎120‎ ‎36‎ ‎4‎ 频率 ‎0.2‎ m ‎0.18‎ ‎0.02‎ 本次问卷调查抽取的样本容量为_______，表中m的值为_______‎ ‎11. 已知两圆内切，圆心距 ，一个圆的半径，那么另一个圆的半径为 ‎ ‎12. 用同样规格的黑白两种颜色的正方形瓷砖，按下图的方式铺地板，则第（5）个图形中有黑色瓷砖 __________块，第个图形中需要黑色瓷砖__________块（用含的代数式表示）．‎ ‎（1）‎ ‎（2）‎ ‎（3）‎ ‎……‎ 三、解答题(本题共30分，每小题5分)‎ ‎13．计算: ‎ ‎14.求不等式组 的正整数解.‎ ‎15. 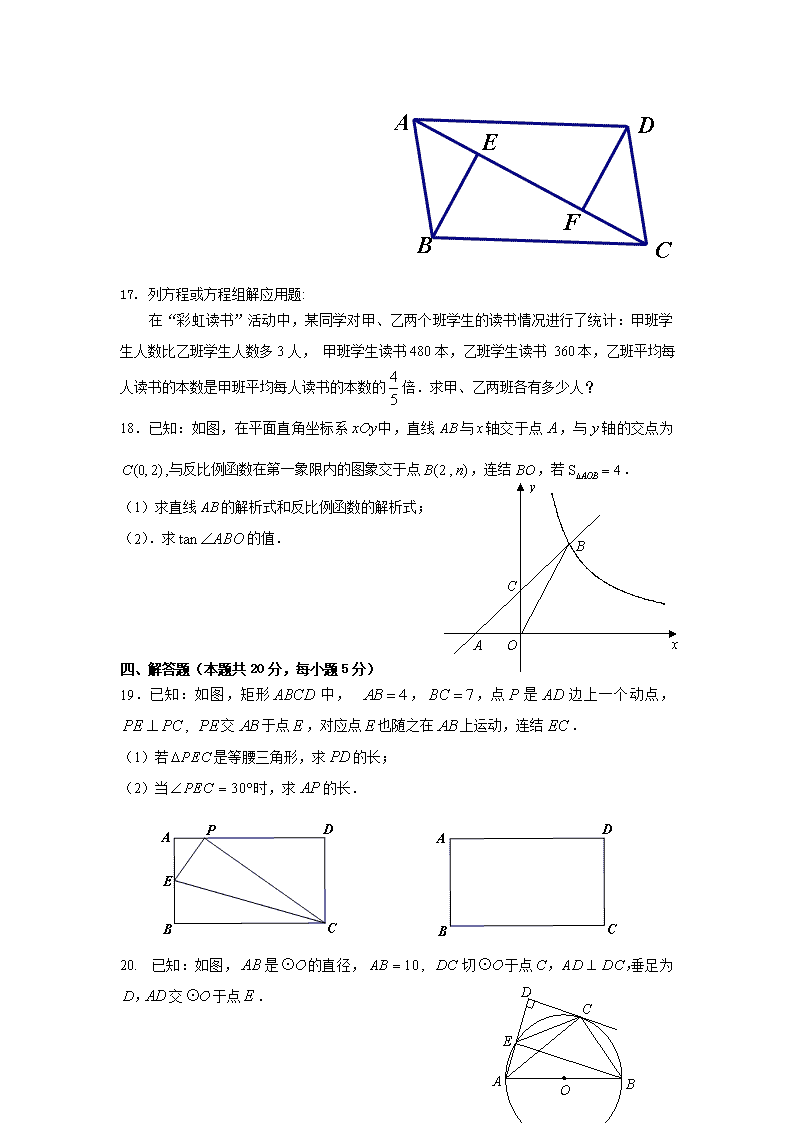已知，求代数式的值.‎ ‎16. 已知：如图，四边形是平行四边形，于，于.‎ 求证：.‎ ‎ ‎ ‎17. 列方程或方程组解应用题:‎ 在“彩虹读书”活动中，某同学对甲、乙两个班学生的读书情况进行了统计：甲班学生人数比乙班学生人数多3人， 甲班学生读书480本，乙班学生读书 360本，乙班平均每人读书的本数是甲班平均每人读书的本数的倍．求甲、乙两班各有多少人？‎ A B C O x y ‎18．已知：如图，在平面直角坐标系中，直线与轴交于点，与轴的交点为,与反比例函数在第一象限内的图象交于点，连结，若．‎ ‎（1）求直线的解析式和反比例函数的解析式；‎ ‎（2）．求的值．‎ 四、解答题（本题共20分，每小题5分）‎ ‎19．已知：如图，矩形ABCD中， ，，点P是AD边上一个动点，, 交于点，对应点也随之在上运动，连结．‎ ‎（1）若是等腰三角形，求的长；‎ ‎（2）当时，求的长．‎ D C B O A E ‎ ‎ ‎20. 已知：如图，是的直径，, 切于点垂足为交于点．‎ ‎（1）求证：;‎ ‎（2）若, 求的长．‎ ‎21. 为了解某住宅区的家庭用水量情况，从该住宅区中随机抽样调查了50户家庭去年每个月的用水量，统计得到的数据绘制了下面的两幅统计图．图1是去年这50户家庭月总用水量的折线统计图，图2是去年这50户家庭月总用水量的不完整的频数分布直方图．‎ 月份 ‎550‎ ‎500‎ ‎600‎ ‎650‎ ‎700‎ ‎800‎ ‎750‎ ‎12‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎•‎ 月总用水量（米3）‎ ‎•‎ ‎•‎ ‎•‎ ‎•‎ ‎•‎ ‎•‎ ‎•‎ ‎•‎ ‎•‎ ‎•‎ ‎•‎ 图1‎ ‎（1）根据图1提供的信息，补全图2中的频数分布直方图；‎ ‎（2）在抽查的50户家庭去年月总用水量这12个数据中，极差是 ‎ 米3，众数是 米3，中位数是 米3；‎ ‎（3）请你根据上述提供的统计数据，估计该住宅区今年每户家庭平均每 月的用水量是多少米3？‎ ‎22．请阅读下列材料：‎ 问题：现有5个边长为1的正方形，排列形式如图1，请把它们分割后拼接成一个新的正方形．要求：画出分割线并在正方形网格图（图中每个小正方形的边长均为1）中用实线画出拼接成的新正方形．‎ 小东同学的做法是：设新正方形的边长为x（x >0）. 依题意，割补前后图形面积相等, 有, 解得．由此可知新正方形的边长等于两个小正方形组成的矩形对角线的长．于是，画出如图2所示的分割线，拼出如图3所示的新正方形．‎ 请你参考小东同学的做法，解决如下问题：‎ ‎（1） 如图4，是由边长为1的5个小正方形组成，请你通过分割，把它拼成一个正方形（在图4上画出分割线，在图4的右侧画出拼成的正方形简图）；‎ ‎（2）如图5，是由边长分别为和的两个正方形组成，请你通过分割，把它拼成一个正方形（在图5上画出分割线，在图5的右侧画出拼成的正方形简图）.‎ 五、解答题（本题共22分，第23题8分，第24题7分，第25题7分）‎ ‎23．已知关于的方程.‎ ‎（1）求证：无论取任何实数时，方程恒有实数根；‎ ‎（2）若为整数，且抛物线与轴两交点间的距离为2，求抛物线的解析式；‎ ‎（3）若直线与（2） 中的抛物线没有交点，求的取值范围.‎ ‎24． 已知：如图，内接于, 为的直径，, 点是上一个动点，连结、和, 与相交于点, 过点作于, 与相交于点,连结和.‎ ‎ (1) 求证：;‎ ‎（2）如图1，若， 求证：；‎ ‎（3) 如图2，设 , 四边形的面积为,求与之间的关系式.‎ ‎ ‎ ‎25．已知，如图，抛物线与轴交于点，与轴交于点，点的坐标为，对称轴是．‎ ‎（1）求该抛物线的解析式；‎ ‎（2）点是线段上的动点，过点作∥，分别交轴、于点P、，连接．当的面积最大时，求点的坐标；‎ ‎（3）在（2）的条件下，求的值.[来源:学科网ZXXK]‎