中考规律探索题及答案 20页

探索规律题 类型一数字规律 ‎1、下面是按一定规律排列的一列数：  ，那么第n个数是  　 ．‎ 解析∵分子分别为1、3、5、7，…，∴第n个数的分子是2n﹣1。  ∵4﹣3=1=1 2 ，7﹣3=4=2 2 ，12﹣3=9=3 2 ，19﹣3=16=4 2 ，…，∴第n个数的分母为n 2 +3。 ∴第n个数是  。‎ 2、 观察下列等式：，，，，，，。试猜想，的个位数字是_____ 。‎ 解析本题主要考查规律探索。‎ 观察等式：，，，，，可得，次方的个位数字是，次方的个位数字是，次方的个位数字是，次方的个位数字是，次方的个位数字是，个位数字的变化是以、、、为周期，即周期为，又因为，所以的个位数字与的个位数字相同为。‎ 故本题正确答案为。考点规律探索。‎ ‎3、古希腊数学家把数1,3,6,10,15,21,叫做三角形数,它有一定的规律性,若把第一个三角形数记为,第二个三角形数记为,第n个三角形数记为,则 ‎ ‎ ‎．‎ 答案 ‎ 解:, ═, , ═, ═,… ,, 则,‎ 因此，本题正确答案是:.‎ 解析根据三角形数得到,,,,,即三角形数为从1到它的顺号数之间所有整数的和,即、,然后计算可得.‎ ‎4、按一定规律排列的一列数：，，，，，，，，请你仔细观察，按照此规律对应的数字应为_____ 。‎ 答案 解析本题主要考查规律探索。‎ 将中间两个化为分数之后为：，，，，，，，，观察可知分子是从开始不断递增的奇数，分母是从开始不断递增的质数，那么根据这个规律即可得到。故本题正确答案为。‎ 考点规律探索。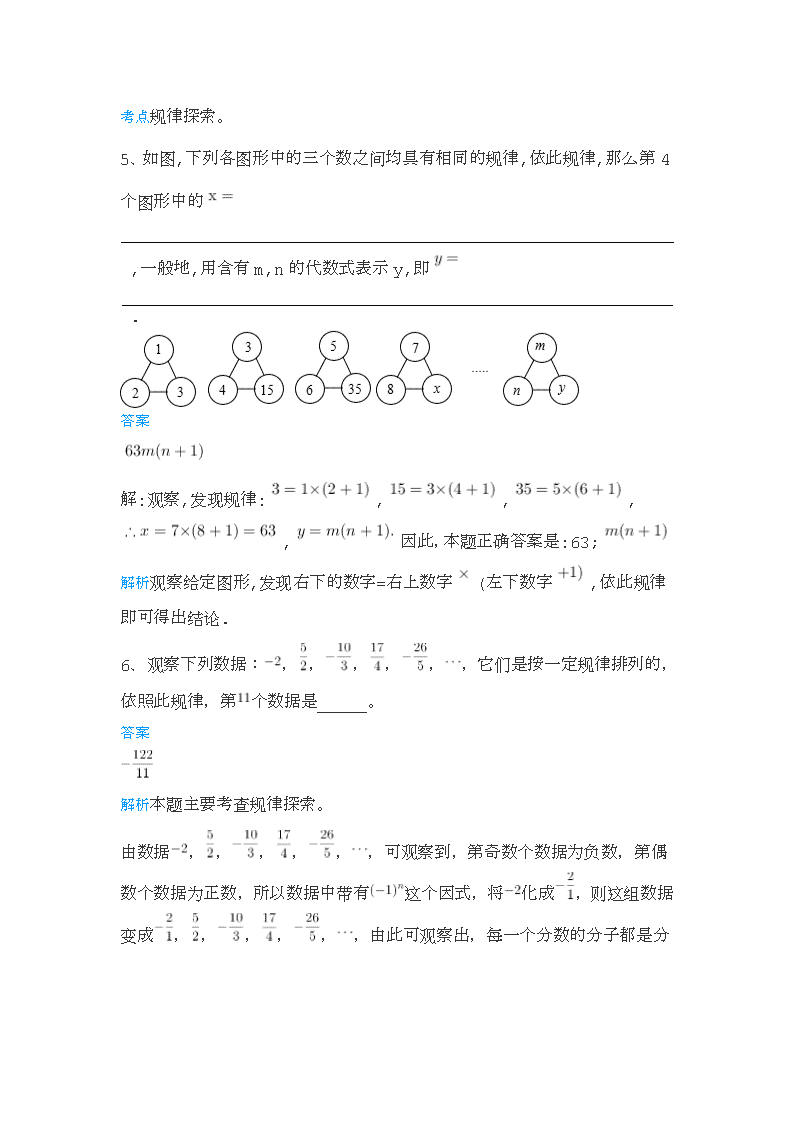‎ ‎5、如图,下列各图形中的三个数之间均具有相同的规律,依此规律,那么第4个图形中的 ‎ ‎ ‎ ,一般地,用含有m,n的代数式表示y,即 ‎ ‎ ‎ .  ‎ 答案 ‎ 解:观察,发现规律:,,,  ,因此，本题正确答案是:63;‎ 解析观察给定图形,发现右下的数字=右上数字(左下数字,依此规律即可得出结论.‎ ‎6、观察下列数据：，，，，，，它们是按一定规律排列的，依照此规律，第个数据是_____。‎ 答案 解析本题主要考查规律探索。‎ 由数据，，，，，，可观察到，第奇数个数据为负数，第偶数个数据为正数，所以数据中带有这个因式，将化成，则这组数据变成，，，，，‎ ‎，由此可观察出，每一个分数的分子都是分母的平方再加，所以这组数据中第个分数为，将代入可得出分数。故本题正确答案为。‎ ‎7、“数学是将科学现象升华到科学本质认识的重要工具”，比如在化学中，甲烷的化学式CH4，乙烷的化学式是C2H6，丙烷的化学式是C3H8，…，设碳原子的数目为n（n为正整数），则它们的化学式都可用下列哪个式子来表示（ ）‎ A.CnH2n+2 B.CnH2n C.CnH2n-2 D.CnHn+3‎ 答案此题答案为：A.‎ 解：设碳原子的数目为n（n为正整数）时，氢原子的数目为an，‎ 观察发现：a1＝4＝2×1+2，a2＝6＝2×2+2，a3＝8＝2×3+2，…，‎ ‎∴an＝2n+2.‎ ‎∴碳原子的数目为n（n为正整数）时，它的化学式为CnH2n+2.故选A.‎ 解析【考点提示】本题主要考查探究规律，解题的关键是找出碳原子与氢原子数量之间的关系．‎ ‎【解题方法提示】设碳原子的数目为n（n为正整数）时，氢原子的数目为an，列出部分an的值；‎ 根据数值的变化找出变化规律“an＝2n+2”，依次规律即可解决问题．‎ ‎8、从“特殊到一般”是数学上常用的一种思维方法.例如,“你会比较与的大小吗?”我们可以采用如下的方法: (1)通过计算比较下列各式中两数的大小:(填“”、“”或“=”) ①‎ ‎②‎ ‎,③‎ ‎,④‎ ‎ (2)由(1)可以猜测与 (n为正整数)的大小关系: 当n 时,;当n 时,;     (3)根据上面的猜想,可以知道: (填“”、“”或“=”).‎ 答案 ‎＜ ＜ ＞ ＞ ≤2 ≥3 ＞ 解:(1)①,,故; ②,,故; ③,,故; ④,,故. 因此，本题正确答案是:①;②;③;④. (2)结合(1)的结论,可以得出猜测结果: 当时,;当时,. 因此，本题正确答案是:;. (3), .因此，本题正确答案是:.‎ 解析先找出各组数的值,再进行比较,即可得出结论; (2)结合(1)结论,即可得出猜测的结论; (3)由,结合(2)猜测的结论,得出结果.‎ 类型二 数式规律 ‎1、（11·曲靖）将一列整式按某种规律排成x，－2x2，4x3，－8x4，16x5…则排在第 六个位置的整式为________．‎ 答案－32‎ 解析符号的规律：n为奇数时，单项式为正号，n为偶数时，符号为负号； 系数的绝对值的规律：第n个对应的系数的绝对值是2n-1． 指数的规律：第n个对应的指数是n． 解：根据分析的规律，得：第六个位置的整式为：-25x6=-32x6．‎ 故答案为：-32x6． 此题考查的知识点是单项式，确定单项式的系数和次数时，把一个单项式分解成数字因数和字母因式的积，是找准单项式的系数和次数的关键．分别找出单项式的系数和次数的规律也是解决此类问题的关键．‎ ‎2、已知，，，，（为正整数，且，），则_____。（用含有的代数式表示）‎ 答案 解析本题主要考查分式的基本性质和规律探索。‎ ‎，，，所以规律以为周期循环，因为可以整除，所以。故本题正确答案为。‎ 考点分式的基本性质，规律探索。‎ ‎3、观察下面计算过程: ; ; 你发现了什么规律?用含n的式子表示这个规律,并用你发现的规律直接写出 的值.‎ 答案 解:, , , ,当时,上式.‎ 解析所求式子利用平方差公式化简,计算即可得到结果.‎ ‎4、观察下来等式：‎ 第一层                1+2=3‎ 第二层                4+5+6=7+8‎ 第三层           9+10+11+12=13+14+15‎ 第四层       16+17+18+19+20=21+22+23+24‎ ‎…‎ 在上述数字宝塔中，从上往下数，数字 2016 在第 ___ 层。‎ 答案由题可知：每一层的第一个数：第 n 层的第一个数为 n2 ，‎ ‎∵442=1936,452=2025 ，∴ 数字 2016 在第 44 层，故答案为： 44.‎ 解析观察发现：第n层的第一个数为n 2，所以要看2016介于哪两个数的平方之间，计算44 2=1936，45 2=2025，  由此得：数字2016在第44层．‎ ‎5、观察下列算式: (1), (2), (3), (4), … 请你在察规律解决下列问题 (1)填空:‎ ‎ ‎ ‎×‎ ‎ ‎ ‎. (2)写出第n个式子(用含n的式子表示),并证明.‎ 答案2013 2017 解:(1)由以上四个等式可以看出: 每一个等式第一个因数等于序号数,第二个因数比第一个大4,等式右边的底数比第一个数大2;所以有:‎ ‎. 答案为:2013,2017; (2)第n个等式为:; 左边右边 成立.‎ 解析 (1) 每一个等式第二个因数比第一个大4,然后都加4,等式右边的底数比第一个数大2;反之可由最后一数反推得到. (2)设第一个数是n,那么第二个因数即为,等式右边的底数则为,表示出等式即可.‎ ‎6、有一列按一定顺序和规律排列的数：第一个数是；第二个数是；第三个数是；对任何正整数，第个数与第个数的和等于。‎ ‎（1）经过探究，我们发现：；；。设这列数的第五个数为，那么，，，哪个正确？请你直接写出正确的结论。‎ ‎（2）请你观察第个数、第个数、第个数，猜想这列数的第个数（即用正整数表示第个数），并且证明你的猜想满足“第个数与第个数的和等于”。‎ ‎（3）设表示，，，，这个数的和，即，求证：。‎ 答案 ‎（1）。‎ ‎（2）由题意可知，第个数为，第个数为。第个数与第个数的和为。‎ ‎（3）因为，，，，，，将上述个不等式式子依次相加可得，，即，得证。‎ 解析本题主要考查规律探索和分式的运算。‎ ‎（1）由已知规律可得，。‎ ‎（2）先根据已知规律写出第个数和第个数，再根据分式的运算求和化简即可求解。‎ ‎（3）将这列数依次根据展开，然后再全部相加即可得证结论。‎ 考点分式的运算，规律探索。‎ 类型三 图形规律 一、 图形累加规律 ‎1、如图是一组有规律的图案，它们是由边长相同的小正方形组成，其中部分小正方形涂有阴影，依此规律，第个图案中有_____个涂有阴影的小正方形（用含有的代数式表示）。‎ 答案 解析本题主要考查规律探索。‎ 由题意可知，第，，个图案中分别有，，个涂有阴影的小正方形。其中，，。由此可以推出，第个图案共有个涂有阴影的小正方形。故本题正确答案为。‎ 考点规律探索。‎ ‎2、图都是由同样大小的黑棋子按一定规律摆出的图案,第①个图案有4个黑棋子,第②个图案有9个黑棋子,第③个图案有14个黑棋子,.依次规律,第n个图案有 ‎ ‎ 个黑棋子.(用含n的代数式表示)‎ 答案 ‎ 解:观察图①有个黑棋子; 图②有个黑棋子; 图③有个黑棋子; 图④有个黑棋子; … 图n有个黑棋子,因此，本题正确答案是.‎ 解析仔细观察每一个图形中黑棋子的个数与图形序列号的关系,找到规律,利用规律求解即可.‎ ‎3、下列图案是用长度相同的火柴棒按一定规律拼搭而成，图案1需根火柴棒，图案2需根火柴棒，，按此规律，图案7需_____根火柴棒。‎ 答案 解析本题主要考查规律探索。‎ 图案1中需要的火柴数为，图案2中需要的火柴数为，图案3中需要的火柴数为，，图案n中需要的火柴数为，所以图案7中需要的火柴数为。‎ 故本题正确答案为。考点规律探索。‎ ‎5、小李用围棋子排成下列一组有规律的图案，其中第个图案有枚棋子，第个图案有枚棋子，第个图案有枚棋子，第个图案有枚棋子，，那么第个图案的棋子数是_____枚。‎ 答案 解析本题主要考查规律探索。‎ 由题意可知，在第奇数个图案的时候增加枚棋子，在第偶数个图案的时候增加枚棋子，以此规律进行排列，第个图案有枚棋子，第个图案有枚棋子，第个图案有枚棋子，第个图案有枚棋子，第个图案有枚棋子。‎ 故本题正确答案为。‎ ‎6、(2016徐州)17.如图，每个图案都是由大小相同的正方形组成，按照此规律，第n个图形中这样的正方形的总个数可用含n的代数式表示为______________。        ‎ 第1个 第2个 第3个 答案 第一个图形，正方形个数：2 ,第二个图形，正方形个数：2+4  第三个图形，正方形个数：2+4+6 第n个图形，正方  形个数：2+4+6+8+....+2n=n(n+1) 故答案为n(n+1)。‎ ‎7、如图,在数轴上,,P两点表示的数分别是1,2,,关于点O对称,,关于点P对称,,关于点O对称,,关于点P对称依次规律,则点表示的数是 ‎ ‎ ‎． ‎ 答案 ‎ 解:根据对称的性质得:表示的数为-1,表示的数为5,表示的数为-5,表示的数为9,表示的数为-9,表示的数为13, 表示的数为,表示的数为17,表示的数为,表示的数为21,表示的数为,表示的数为25, 则表示的数为.因此，本题正确答案是:.‎ ‎8、将一些半径相同的小圆按如图所示的规律摆放，请仔细观察，第个图形有_____个小圆。（用含的代数式表示）‎ 答案 ‎0.6M ‎02:13‎ 解析本题主要考查整式探索与表达规律。‎ 据观察，第个图形有个小圆，第个图形有个小圆，第个图形有个小圆，第个图形有个小圆。‎ 故本题正确答案为。考点探索图形中的规律。‎ ‎9、观察如图所示的钢管的截面图，则第个图的钢管数是_____ 。（用含的式子表示）‎ 答案 ‎0.7M ‎02:26‎ 解析本题主要考查规律探索。‎ 设第个图的钢管数为，则由题可知，当时，。当时，，当时，，，所以。‎ 故本题正确答案为。‎ ‎10、下列图形都是由同样大小的小圆圈按一定规律所组成的，其中第①个图形中一共有个小圆圈，第②个图形中一共有个小圆圈，第③个图形中一共有个小圆圈，，按此规律排列下去，第⑦个图形中小圆圈的个数为（  ）。‎ A:  B:  C:  D: ‎ 答案D解析本题主要考查规律探索。‎ 观察图可知，第①个图中小圆圈有个，第②个图中小圆圈的个数为，第③个图中小圆圈的个数为，以此类推，第⑦个图中小圆圈的个数为。‎ 故本题正确答案为D。考点规律探索。‎ ‎11、图①是一个三角形,分别连接这个三角形三边的中点得到图②,再分别连接图②中间小三角形三边的中点,得到图③. (1)图②有 ‎ ‎ 个三角形;图③有 ‎ ‎ 个三角形. (2)按上面的方法继续下去,第n个图形中有多少个三角形?(用n的代数式表示结论) (3)有没有一个图形中存在2016个三角形?如果存在,请求出是第几个三角形;如果不存在,请说明理由. ‎ 答案 5 9 解:根据图形的变化可以知道每个图形比前一个图形多4个三角形. (1)由发现的规律可以知道图②有个三角形;图③有个三角形.因此，本题正确答案是:5;9. (2). 故按上面的方法继续下去,第n个图形中有个三角形. (3)令,计算得出, 商出现了余数,即得数不是整数, 没有一个图形中存在2016个三角形.‎ 解析(1)根据图形的变化可发现每个图形比前一个图形多4个三角形,结合图①有一个三角形即可得出结论;(2)根据图形的变化可发现每个图形比前一个图形多4个三角形,而图形①只有一个三角形,用含n的代数式表示出结论即可;(3)结合(2)的结论,令三角形的个数等于2016,看n的值是否为整数,是的话则第n个图形就是所求,如果不是,则不存在.‎ 一、 图形成倍递变 ‎12、如图，在中，，点，分别是，边的中点，点，分别是，的中点，点，分别是，的中点，按这样的规律下去，的长为_____（为正整数）。‎ 答案 ‎1.6M ‎06:12‎ 解析本题主要考查规律探索。‎ 因为点、分别是边、的中点，所以是的中位线。根据三角形中位线定理可知，故。又因为点、分别是边、的中点，所以是的中位线，所以，按此规律，所以。故本题正确答案为。考点规律探索。‎ ‎13、如图，由若干盆花摆成图案，每个点表示一盆花，几何图形的每条边上（包括两个顶点）都摆有n（n≥3）盆花，每个图案中花盆总数为S，按照图中的规律可以推断S与n（n≥3）的关系是 ‎ n（n-1） ‎ ‎．‎ 答案 解：n=3时，S=6=3×3-3=3，  n=4时，S=12=4×4-4，  n=5时，S=20=5×5-5，  …，  依此类推，边数为n数，S=n•n-n=n（n-1）． 故答案为：n（n-1）．‎ 解析根据各图形的排列规律，用边数乘以每一条边上的花盆数，因为顶点上的花盆被计算了两次，所以再减去顶点数整理即可．‎ 本题是对图形变化规律的考查，需要注意顶点处的花盆被计算了两次，这是本题容易出错的地方．‎ ‎14、如图，在平面直角坐标系中，边长为的正方形的两边在坐标轴上，以它的对角线为边作正方形，再以正方形的对角线为边作正方形，以此类推，则正方形的顶点的坐标是_____ 。‎ 答案 解析本题主要考查规律探索。‎ 由题意可以推出，，，，，，，，，，可以看出，，，分别位于第一、二、三、四象限，且横纵坐标的绝对值相等，分别等于，，，。而，可以推断出位于第四象限，其坐标为，观察到的规律，可知在轴正半轴上，其坐标为。故本题正确答案为。‎ 考点规律探索 考点几何之规律探索。‎ 考点规律探索，三角形的基本概念，等腰三角形。‎ 一、 图形循环规律 ‎17、下列一串梅花图案是按一定规律排列的,请你仔细观察,在前2016个梅花图案中,共有 ‎ ‎ 个“”图案.‎ 答案 ‎504 解:, ∴有504个,因此，本题正确答案是:504.‎ 解析 察图形可以知道,这组图案的排列规律是:四个图案一个循环周期,每个周期都有一个,由此计算出第2016个图案经历了几个周期即可解答.‎ ‎18、‎ 一组“穿心箭”按如下规律排列，照此规律，画出支“穿心箭”是_____ 。‎ 答案 ‎0.解析本题主要考查规律探索。‎ 观察“穿心箭”变化可得，奇数支的“穿心箭”心数为，偶数支的“穿心箭”心数为，是奇数，所以应为颗心。箭的指向以向右上角、向右下角和向右为周期变化，可以被整除，所以箭的指向应为向右，故第支“穿心箭”是。故本题正确答案为。‎