2014辽宁省沈阳市中考数学 12页

2014 年辽宁省沈阳市中考试题 数 学 （满分 150 分，考试时间 120 分钟） 参考公式：抛物线 y=ax2+bx+c 的顶点坐标是（ - b 2a, 4ac- b2 4a ）.对称轴是直线 x= - b 2a . 一、选择题（下面各题的备选答案中，只有一个答案是正确的，每小题 3 分，共 24 分） 1．(2014 年辽宁省沈阳市，1，3 分) 0 这个数是（ ） A．正数 B．负数 C．整数 D．无理数 【答案】C 2．(2014 年辽宁省沈阳市，2，3 分)2014 年端午节小长假期间，沈阳某景区接待游客约为 85000 人，将数据 85000 用科学记数法表示为（ ） A．85×103 B．8.5×104 C．0.85×105 D．8.5×105 【答案】B 3．(2014 年辽宁省沈阳市，3，3 分)某几何体的三视图如图所示，这个几何体是（ ） A．圆柱 B．三棱柱 C．长方体 D．圆锥 【答案】C 4．(2014 年辽宁省沈阳市，4，3 分)已知一组数据：1，2，6，3，3，下列说法正确的是（ ） A．众数是 3 B．中位数是 6 C．平均数是 4 D．方差是 5 【答案】A 5．(2014 年辽宁省沈阳市，5，3 分)一元一次不等式 x-1≥0 的解集在数轴上表示正确的是 ( ) 【答案】A 6．(2014 年辽宁省沈阳市，6，3 分)正方形是轴对称图形，它的对称轴有（ ） A．2 条 B．4 条 C．6 条 D．8 条 【答案】B 7．(2014 年辽宁省沈阳市，7，3 分) 下列运算正确的是（ ） A．(-x3)2＝-x6 B．x4+x4＝x8 C．x2•x3＝x6 D．xy4÷(-xy)＝-y3 【答案】D 8．(2014 年辽宁省沈阳市，8，3 分)如图，在△ABC 中，点 D 在边 AB 上，BD=2AD，DE//BC 交 AC 于点 E，若线段 DE=5，则线段 BC 的长为（ ） A. 7.5 B. 10 C.15 D.20 【答案】C 二、填空题（每小题 4 分，共 32 分） 9．(2014 年辽宁省沈阳市，9，4 分) 计算： 9 ＝__________. 【答案】3 10. (2014 年辽宁省沈阳市，10，4 分) 分解因式： 2m2 +10m＝__________. 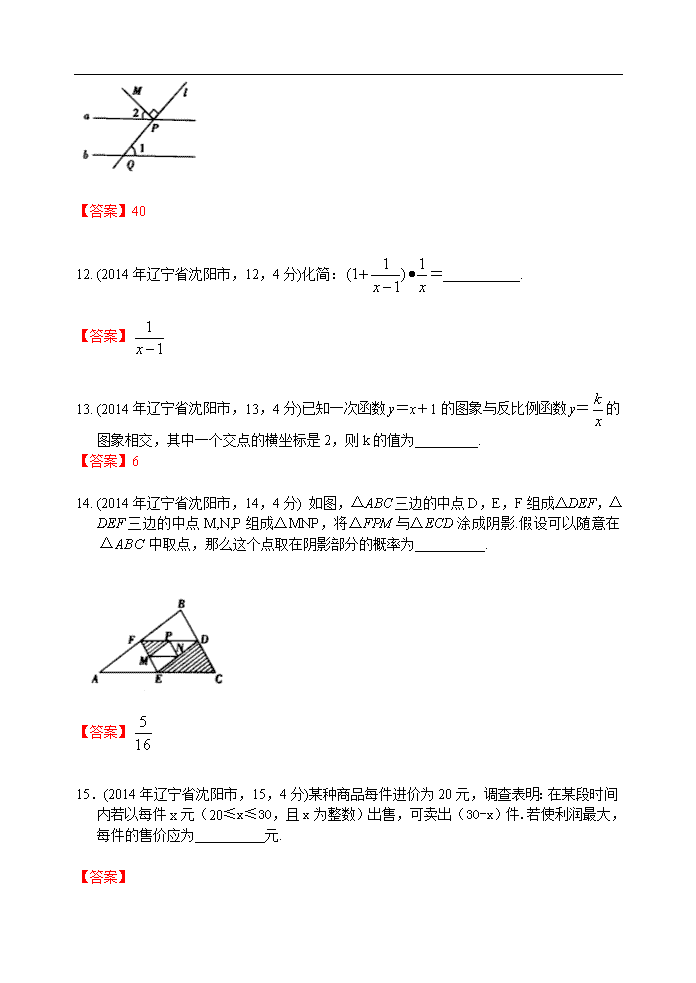【答案】2m(m+5) 11. (2014 年辽宁省沈阳市，11，4 分) 如图，直线 a//b,n 直线 l 与 a 相交于点 P，与直线 b 相交于点 Q，PM⊥l 于点 P，若∠1=50 °，则∠2= °. 【答案】40 12. (2014 年辽宁省沈阳市，12，4 分)化简： (1+ 1 x-1)· 1 x ＝___________. 【答案】 1 x-1 13. (2014 年辽宁省沈阳市，13，4 分)已知一次函数 y＝x＋1 的图象与反比例函数 y＝ k x 的 图象相交，其中一个交点的横坐标是 2，则 k 的值为_________. 【答案】6 14. (2014 年辽宁省沈阳市，14，4 分) 如图，△ABC 三边的中点 D，E，F 组成△DEF，△ DEF 三边的中点 M,N,P 组成△MNP，将△FPM 与△ECD 涂成阴影.假设可以随意在 ABC△ 中取点，那么这个点取在阴影部分的概率为__________. 【答案】 5 16 15．(2014 年辽宁省沈阳市，15，4 分)某种商品每件进价为 20 元，调查表明：在某段时间 内若以每件 x 元（20≤x≤30，且 x 为整数）出售，可卖出（30-x）件.若使利润最大， 每件的售价应为__________元. 【答案】 16．(2014 年辽宁省沈阳市，16，4 分)（每题 7 分，共 14 分）如图，□ABCD 中，AB>AD， AE,BE,CM,DM 分别为∠DBA，∠ABC，∠BCD，∠CDA 的平分线，AE 与 DM 相交于 点 F，BE 与 CM 相交于点 H，连接 EM，若□ABCD 的周长为 42cm，FM=3cm，EF=4cm， 则 EM= cm，AB= cm. 【答案】5;13 三、解答题(第 17、18 小题各 8 分，第 19 小题 10 分，共 26 分) 17. (2014 年辽宁省沈阳市，17，8 分) 先化简，再求值： (a+b)2 -(a-b)2éë ùû·a，其中 a = -1,b= 5. 【答案】解： (a+b)2 -(a-b)2éë ùû·a = a2 + 2ab+b2 - a2 + 2ab-b2éë ùû·a = 4ab·a = 4a2b 当 a=-1，b=5 时，原式=4×（-1）2×5=20. 18．(2014 年辽宁省沈阳市，18，8 分)如图，在矩形 ABCD 中，对角线 AC,BD 相交于点 O， 点 E，F 分别在边 AD，BC 上，且 DE=CF，连接 OE，OF. 求证：OE=OF. 【答案】证明：∵四边形 ABCD 为矩形， ∴∠ADC=∠BCD=90°, AC=BD,OD= 1 2 BD,OC= 1 2 AC. OD=OC. ∴∠ODC=∠OCD. ∴∠ADC-∠ODC =∠BCD-∠OCD,即∠EDO=∠FCO. 又∵DE=CF， ∴△ODE≌△OCF. ∴OE=OF. 19．(2014 年辽宁省沈阳市，19，10 分) 在一个不透明的盒子里有红球、白球、黑球各一 个，它们除了颜色外其余都相同.小明从盒子里随机摸出一球，记录下颜色后放回盒子 里，充分摇匀后，再随机摸出一球，并记录下颜色.请用列表法或画树状图（树形图） 法求小明两次摸出的球颜色不同的概率. 【答案】解： 或画树状（形）图得： 由表格（或树状图/树形图）可知，共有 9 种可能出现的结果，每种结果出现的可能性相同， 其中小明两次摸出的球颜色不同的结果有 6 种：（红球，白球）（红球，黑球）（白球， 红球）（白球，黑球）（黑球，红球）（黑球，白球），所以 P（小明两次摸出的球的颜色 不同）= 6 9 = 2 3 . 四、（每小题 10 分，共 20 分） 20. (2014 年辽宁省沈阳市，20，10 分)2014 年世界杯足球赛于北京时间 6 月 13 日 2 时在 巴西开幕，某媒体足球栏目从参加世界杯球队中选出五支传统强队：意大利队、德国 队、西班牙队、巴西队、阿根廷队，对哪支球队最有可能获得冠军进行了问卷调查.为 了使调查结果有效，每位被调查都只能填写一份问卷，在问卷中必须选择这五支球队 中的一队作为调查结果，这样的问卷才能成为有效问卷.从收集到的 4800 份有效问卷中 随机抽取部分问卷进行了统计，绘制了统计图表的一部分如下： 根据统计图表提供的信息，解答下列问题： （1）a= ,b= ; （2）根据以上信息，请直接．．在答题卡中补全条形统计图； （3）根据抽样调查结果，请你估计在提供有效问卷的这 4800 人中有多少人预测德国队最 有可能获得冠军. 【答案】解：(1) a=30%,b=5% (2) (3)4800×30%=1440(人) 答：大约有 1440 人预测德国队最有可能获得冠军. 21．(2014 年辽宁省沈阳市，21，10 分)某公司今年销售一种产品，1 月份获得利润 20 万 元，由于产品畅销，利润逐月增加，3 月份的利润比 2 月份的利润增加 4.8 万元，假设 该产品利润每月的增长率相同，求这个增长率. 【答案】解：设这个增长率为 x. 依题意得：20（1+x）2-20（1+x）=4.8 解得：x1=0.2,x2=-1.2(不合题意，舍去)，0.2=20% 答：这个增长率为 20%. 五、（本题 10 分） 22．(2014 年辽宁省沈阳市，22，10 分)如图，⊙O 是△ABC 的外接圆，AB 为直径，OD ∥BC 交⊙O 于点 D，交 AC 于点 E，连接 AD，BD，CD. （1）求证：AD=CD； （2）若 AB=10，cos∠ABC= 3 5 ，求 tan∠DBC 的值. 【答案】解：(1)证明：∵AB 为⊙O 直径，∴∠ACB=90°. 又∵OD∥BC, ∴∠AEO=∠ACB=90°. ∴OD⊥AC. ∴ AD=CD.∴AD=CD. (2)解：∵AB=10, ∴OA=OD= 1 2 AB=5. ∵OD∥BC, ∴∠AOE=∠ABC. 在 Rt△AEO 中，OE=OAcos∠AOE= OAcos∠ABC=5× 3 5 =3. ∴DE=OD-OE=5-3=2. 由勾股定理得，AE= AO2 -OE 2 = 52 -32 = 4 . 在 Rt△AED 中，tan∠DAE= DE AE = 2 4 = 1 2 . 又∵∠DBC=∠DAE, ∴tan∠DBC= 1 2 . 六、（本题 12 分） 23．(2014 年辽宁省沈阳市，23，12 分)如图，在平面直角坐标系中，四边形 OABC 的顶 点 O 为坐标原点，点 C 在 x 轴的正半轴上，且 BC⊥OC 于点 C，点 A 的坐标为 2,2 3( ) ,AB= 4 3 ,∠B=60°，点 D 是线段 OC 上一点，且 OD=4，连接 AD. （1）求证：△AOD 是等边三角形； （2）求点 B 的坐标； （3）平行于 AD 的直线 l 从原点 O 出发，沿 x 轴正方向平移.设直线 l 被 四边形 OABC 截 得的线段长为 m，直线 l 与 x 轴交点的横坐标为 t. ①当直线 l 与 x 轴的交点在线段 CD 上（交点不与点以，D 重合）时，请直接写出 m 与 t 的函数关系式（不必写出自变量 t 的取值范围）； ②若 m=2,请直接．．写出此时直线 l 与 x 轴的交点坐标. 【答案】解： (1)证明：过点作 AM⊥x 轴于点 M， ∵点 A 的坐标为 2,2 3( ) ，∴OM=2,AM= 2 3 . ∴在 Rt△AOM 中，tan∠AOM= AM OM = 2 3 2 = 3 ,∴∠AOM=60°. 由勾股定理得，OA= OM2 + AM2 = 22 + 2 3( )2 = 4 ∵OD=4, ∴OA=OD. ∴△AOD 是等边三角形. (2)解：过点 A 作 AN⊥BC 于点 N， ∵BC⊥OC，AM⊥x 轴， ∴∠BCM=∠CMA=∠ANC =90°. ∴四边形 ANCM 为矩形，∴AN=MC，AM=NC. ∵∠B=60°,AB= 4 3 , ∴在 Rt△ABN 中，AN=AB·sinB= 4 3´ 3 2 =6, ∴BN=AB·cosB= 4 3 ´ 1 2 = 2 3 . ∴AN=MC=6,CN=AM= 2 3 .∴OC=OM+MC=2+6=8, BC=BN+CN= 2 3 + 2 3 = 4 3 . ∴点 B 的坐标为（8， 4 3 ）. (3)① m= 1 2 t+ 2 . ②(2,0),( 32 3 ,0) 七、（本题 12 分） 24．(2014 年辽宁省沈阳市，24，12 分)如图 1，在菱形 ABCD 中，对角线 AC 与 BD 相交于 点 O，AB=13，BD=24，在菱形 ABCD 的外部以 AB 为边作等边三角形 ABE.点 F 是对角线 BD 上一动点（点 F 不与点 B 重合），将线段 AF 绕点 A 在顺时针方向旋转 60°得到线 段 AM，连接 FM. （1）求 AO 的长； （2）如图 2，当点 F 在线段 BO 上，且点 M，F，C 三点在同一条直线上时，求证：AC= 3 AM； （3）连接 EM，若△AEM 的面积为 40，请直接．．写出△AFM 的周长. 温馨提示：考生可以根据题意，在备用图中补充图形，以便作答. 【答案】解：(1)解：∵四边形 ABCD 为菱形，∴AC⊥BD,OB=OD= 1 2 BD. ∵BD=24,∴OB=12. ∴在 Rt△OAB 中，∵AB=13,∴OA= AB2 -OB2 = 132 -122 = 5. (2)证明：∵四边形 ABCD 为菱形，∴BD 垂直平分 AC. ∴FA=FC. ∠FAC=∠FCA. 由已知 AF=AM.∴∠MAF=60°. ∴△AMF 为等边三角形. ∴∠M=∠AFM=60°. ∵点 M，F，C 三点在同一条直线上 ∴∠FAC+∠FCA=∠AFM=60°. ∴∠FAC=∠FCA=30°. ∴∠MAC=∠MAF+∠FAC=60°+30°=90°. 在 Rt△ACM 中，tanM= AC AM ,∴tan60°= AC AM . ∴AC= 3 AM. (3) △AFM 的周长为 3 41. 八、（本题 14 分） 25．(2014 年辽宁省沈阳市，25，14 分) 如图 1，在平面直角坐标系中，二次函数 y= - 4 27 x2 +12 的图象与 y 轴交于点 A，与 x 轴交于点 B，C 两点（点 B 在点 C 的左 侧），连接 AB，AC. （1）点 B 的坐标为 ，点 C 的坐标为 ； （2）过点 C 作射线 CD∥AB，点 M 是线段 AB 上的动点，点 P 是线段 AC 上的动点，且 始终满足 BM=AP（点 M 不与点 A，点 B 重合），过点 M 作 MN∥BC 分别交 AC 于 点 Q，交射线 CD 于点 N（点 Q 不与点 P 重合），连接 PM，PN，设线段 AP 的长为 n. ①如图 2，当 n< 1 2 AC 时，求证：△PAM≌△NCP； ②直接．．用含 n 的代数式表示线段 PQ 的长； ③若 PM 的长为 97 ，当二次函数 y= - 4 27 x2 +12 的图象经过平移同时过点 P 和点 N 时， 请直接．．写出此时的二次函数的表达式. 温馨提示：考生可以根据题意，在备用图中补充图形，以便作答 【答案】解：(1)(-9,0),(9,0). (2)①证明：∵AB∥CD,MN∥BC, ∴四边形 BMNC 为平行四边形. ∴BM=CN.∵BM=AP,∴AP=CN. ∵OC=OB=9,又∵AO⊥BC, ∴AB=AC,∴AB-BM=AC-AP. ∴AM=PC.∵AB∥CD,∴∠MAP=∠PCN.∴△PAM≌△NCP. ②15-2n 或 2n-15. ③ y= - 4 27 x2 +16 9 x+ 4或 y= - 4 27 x2 + 32 9 x-12 .