中考复习之专题十圆完美编辑版 18页

中考复习之专题十 圆 教学准备 一. 教学目标 ‎（1）掌握圆的有关概念和计算 ‎①知道圆由圆心与半径确定，了解圆的对称性．‎ ‎②通过图形直观识别圆的弦、弧、圆心角等基本元素．‎ ‎③利用圆的对称性探索弧、弦、圆心角之间的关系，并会进行简单计算和说理．‎ ‎④探索并了解圆周角与圆心角的关系、直径所对圆周角的特征．‎ ‎⑤掌握垂径定理及其推论，并能进行计算和说理．‎ ‎⑥了解三角形外心、三角形外接圆和圆内接三角形的概念．‎ ‎⑦掌握圆内接四边形的性质 ‎（2）点与圆的位置关系 ‎①能根据点到圆心的距离和半径的大小关系确定点与圆的位置关系．‎ ‎②知道“不在同一直线上的三个点确定一个圆”并会作图．‎ ‎（3）直线与圆的位置关系 ‎①能根据圆心到直线的距离和半径的大小关系确定直线与圆的位置关系．‎ ‎②了解切线的概念．‎ ‎③能运用切线的性质进行简单计算和说理．‎ ‎④掌握切线的识别方法．‎ ‎⑤了解三角形内心、三角形内切圆和圆的外切三角形的概念．‎ ‎⑥能过圆上一点画圆的切线并能利用切线长定理进行简单的切线计算．‎ ‎（4）圆与圆的位置关系 ‎ ‎①了解圆与圆的五种位置关系及相应的数量关系．‎ ‎②能根据两圆的圆心距与两圆的半径之间的数量关系判定两圆的位置关系．‎ ‎③掌握两圆公切线的定义并能进行简单计算 ‎（5）圆中的计算问题 ‎①掌握弧长的计算公式，由弧长、半径、圆心角中已知两个量求第三个量．‎ ‎②掌握求扇形面积的两个计算公式，并灵活运用．‎ ‎③了解圆锥的高、母线等概念．‎ ‎④结合生活中的实例（模型）了解圆柱、圆锥的侧面展开图．‎ ‎⑤会求圆柱、圆锥的侧面积、全面积，并能结合实际问题加以应用．‎ ‎⑥能综合运用基本图形的面积公式求阴影部分面积．‎ 二. 教学难点与重点：‎ 与圆的性质有关的计算、开放题以及与圆和多边形结合的探索题是本单元的重点也是难点．‎ 三. 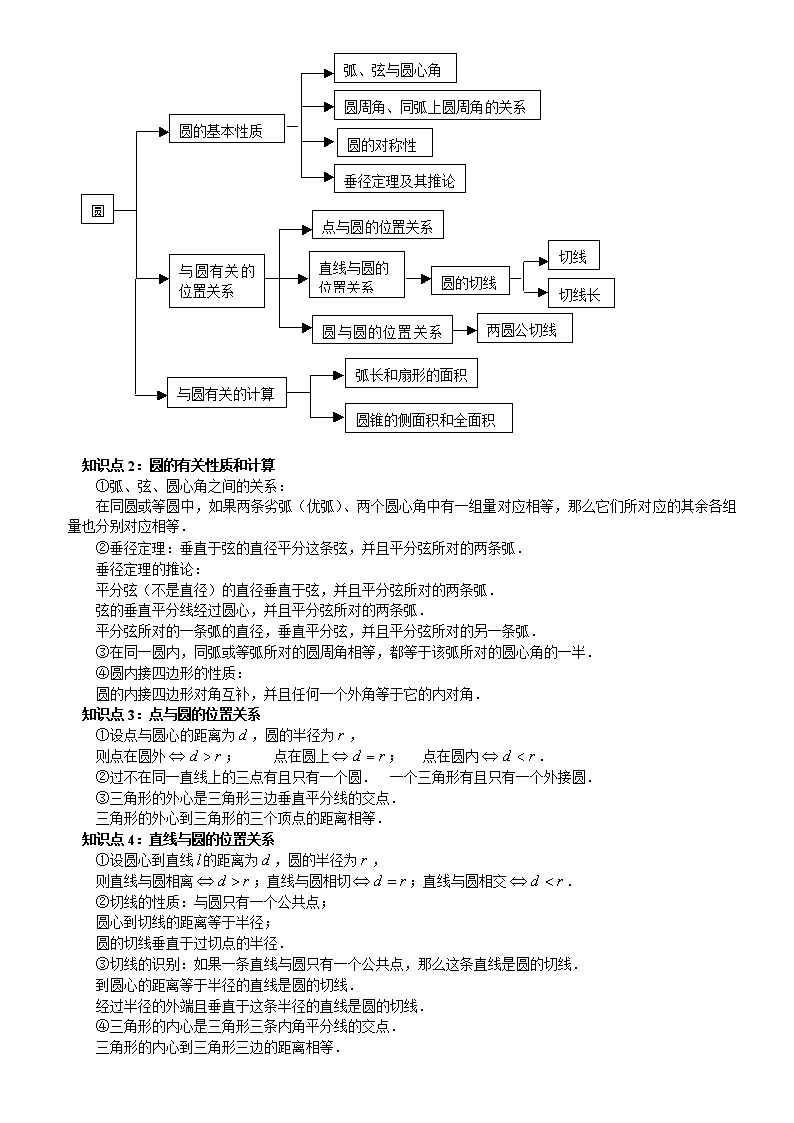知识要点：‎ 知识点1：知识点之间的关系 ‎ ‎ 知识点2：圆的有关性质和计算 ‎①弧、弦、圆心角之间的关系：‎ 在同圆或等圆中，如果两条劣弧（优弧）、两个圆心角中有一组量对应相等，那么它们所对应的其余各组量也分别对应相等．‎ ‎②垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．‎ 垂径定理的推论：‎ 平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧．‎ 弦的垂直平分线经过圆心，并且平分弦所对的两条弧．‎ 平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧．‎ ‎③在同一圆内，同弧或等弧所对的圆周角相等，都等于该弧所对的圆心角的一半．‎ ‎④圆内接四边形的性质：‎ 圆的内接四边形对角互补，并且任何一个外角等于它的内对角．‎ 知识点3：点与圆的位置关系 ‎①设点与圆心的距离为，圆的半径为，‎ 则点在圆外； 点在圆上； 点在圆内．‎ ‎②过不在同一直线上的三点有且只有一个圆． 一个三角形有且只有一个外接圆．‎ ‎③三角形的外心是三角形三边垂直平分线的交点．‎ 三角形的外心到三角形的三个顶点的距离相等．‎ 知识点4：直线与圆的位置关系 ‎①设圆心到直线的距离为，圆的半径为，‎ 则直线与圆相离；直线与圆相切；直线与圆相交．‎ ‎②切线的性质：与圆只有一个公共点；‎ 圆心到切线的距离等于半径；‎ 圆的切线垂直于过切点的半径．‎ ‎③切线的识别：如果一条直线与圆只有一个公共点，那么这条直线是圆的切线．‎ 到圆心的距离等于半径的直线是圆的切线．‎ 经过半径的外端且垂直于这条半径的直线是圆的切线．‎ ‎④三角形的内心是三角形三条内角平分线的交点．‎ 三角形的内心到三角形三边的距离相等．‎ ‎⑤切线长：圆的切线上某一点与切点之间的线段的长叫做这点到圆的切线长．‎ ‎⑥切线长定理：从圆外一点引圆的两条切线，它们的切线长相等．‎ 这一点和圆心的连线平分这两条切线的夹角．‎ 知识点5：圆与圆的位置关系 ‎①圆与圆的位置关系有五种：外离、外切、相交、内切、内含．‎ ‎ 设两圆心的距离为，两圆的半径为，则两圆外离 ‎ 两圆外切 ‎ 两圆相交 ‎ 两圆内切 ‎ 两圆内含 ‎ ‎②两个圆构成轴对称图形，连心线（经过两圆圆心的直线）是对称轴．‎ 由对称性知：两圆相切，连心线经过切点．两圆相交，连心线垂直平分公共弦．‎ ‎③两圆公切线的定义：和两个圆都相切的直线叫做两圆的公切线．‎ 两个圆在公切线同旁时，这样的公切线叫做外公切线．‎ 两个圆在公切线两旁时，这样的公切线叫做内公切线．‎ ‎④公切线上两个切点的距离叫做公切线的长． ‎ 知识点6：与圆有关的计算 ‎①弧长公式： 　　　　 扇形面积公式：‎ ‎（其中为圆心角的度数，为半径）‎ ‎②圆柱的侧面展开图是矩形．‎ 圆柱体也可以看成是一个矩形以矩形的一边为轴旋转而形成的几何体．‎ 圆柱的侧面积＝底面周长×高 ‎ 圆柱的全面积＝侧面积＋2×底面积 ‎③圆锥的侧面展开图是扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．‎ 圆锥体可以看成是由一个直角三角形以一条直角边为轴旋转而成的几何体．‎ ‎④圆锥的侧面积＝×底面周长×母线；圆锥的全面积＝侧面积＋底面积 例题精讲 例1. △ABC中，AC＝6，BC＝8，∠C＝90°，以点C为圆心，CA为半径的圆与AB交于点D，求AD的长．‎ ‎【分析】圆中有关弦的计算问题通常利用垂径定理构造直角三角形求解，所以作CH⊥AB，这只要求出AH的长就能得出AD的长．‎ ‎【解】作CH⊥AB，垂足为H ‎∵∠C＝90°，AC＝6，BC＝8　　　∴AB＝10‎ ‎∵∠C＝90°，　CH⊥AB　　　‎ ‎∴‎ 又∵AC＝6， AB＝10　　　　∴　AH＝3.6‎ ‎∵CH⊥AB　　　∴AD＝2AH ∴AD＝7.2‎ 答：AD的长为7.2. ‎ ‎【说明】解决与弦有关的问题，往往需要构造垂径定理的基本图形——由半径、弦心距、弦的一半构成的直角三角形，它是解决此类问题的关键．定理的应用必须与所对应的基本图形相结合，同学们在复习时要特别注重基本图形的掌握．‎ 例2. （1）如图，△ABC内接于⊙O，AB为直径，∠CAE＝∠B，试说明AE与⊙O相切于点A．‎ ‎（2）在（1）中，若AB为非直径的弦，∠CAE＝∠B，AE还与⊙O相切于点A吗？请说明理由．‎ ‎【分析】第（1）小题中，因为AB为直径，只要再说明∠BAE为直角即可．第（2）小题中，AB为非直径的弦，但可以转化为第（1）小题的情形．‎ ‎【解】（1）∵AB是⊙O的直径　　　　∴∠C＝90°‎ ‎∴∠BAC＋∠B＝90°‎ 又∵∠CAE＝∠B ‎∴∠BAC＋∠CAE ＝90°‎ 即∠BAE ＝90°‎ ‎∴AE与⊙O相切于点A.‎ ‎（2）连结AO并延长交⊙O于D，连结CD.‎ ‎∵AD是⊙O的直径　　　　∴∠ACD＝90°‎ ‎∴∠D＋∠CAD＝90°‎ 又∵∠D＝∠B ∴∠B＋∠CAD＝90°‎ 又∵∠CAE ＝∠B ∴∠CAE＋∠CAD＝90°‎ 即∠EAD ＝90° ∴AE仍然与⊙O相切于点A. ‎ ‎【说明】本题主要考查切线的识别方法．渗透了“由特殊到一般”的数学思想方法，这对于学生的探索能力的培养非常重要．‎ 例3. 如图，已知⊙O的直径AB垂直于弦CD于E，连结AD、BD、OC、OD，且OD＝5．‎ ‎（1）若，求CD的长．‎ ‎（2）若∠ADO：∠EDO＝4：1，求扇形OAC（阴影部分）的面积（结果保留）．‎ ‎【分析】图形中有 “直径对直角”，这样就出现了“直角三角形及斜边上的高”的基本图形，求CD的长就转化为求DE的长．第（2）小题求扇形OAC的面积其关键是求∠AOD的度数，从而转化为求∠AOD的大小．‎ ‎【解】（1）∵AB是⊙O的直径，OD＝5‎ ‎∴∠ADB＝90°，AB＝10‎ 又∵在Rt△ABD中，‎ ‎∴‎ ‎∵∠ADB＝90°，AB⊥CD ‎∴BD2＝BE·AB ‎∵AB＝10 ‎ ‎∴BE＝‎ 在Rt△EBD中，由勾股定理得 ‎∴‎ 答：CD的长为．‎ ‎（2）∵AB是⊙O的直径，AB⊥CD ‎∴‎ ‎∴∠BAD＝∠CDB，∠AOC＝∠AOD ‎∵AO＝DO　　　　∴∠BAD＝∠ADO ‎∴∠CDB＝∠ADO 设∠ADO＝4k，则∠CDB＝4k ‎∵∠ADO＋∠EDO＋∠EDB＝90°‎ ‎∴　　　　　得k＝10°‎ ‎∴∠AOD＝180°－（∠OAD＋∠ADO）＝100°‎ ‎∴∠AOC＝∠AOD＝100°‎ 则 答：扇形OAC的面积为 ‎【说明】本题涉及到了圆中的重要定理、直角三角形的边角关系、扇形面积公式等知识点的综合，考查了学生对基本图形、基本定理的掌握程度．求DE长的方法很多，可以用射影定理、勾股定理，也可以运用面积关系来求，但都离不开“直角三角形及斜边上的高”这个基本图形．解题中也运用了比例问题中的设k法，同时也渗透了“转化”的思想方法．‎ 例4. 半径为2.5的⊙O中，直径AB的不同侧有定点C和动点P．已知BC ：CA＝4 ： 3，点P在半圆AB 上运动（不与A、B两点重合），过点C作CP的垂线，与PB的延长线交于点Q.‎ ‎（1）当点P与点C关于AB对称时，求CQ的长；‎ ‎（2）当点P运动到半圆AB的中点时，求CQ的长； ‎ ‎（3）当点P运动到什么位置时，CQ取到最大值？求此时CQ的长．‎ ‎【分析】当点P与点C关于AB对称时，CP被直径垂直平分，由垂径定理求出CP的长，再由Rt△ACB∽Rt△PCQ，可求得CQ的长．当点P在半圆AB上运动时，虽然P、Q 点的位置在变，但△PCQ始终与△ACB相似，点P运动到半圆AB的中点时，∠PCB＝45°，作BE⊥PC于点E， CP＝PE＋EC. 由于CP与CQ的比值不变，所以CP取得最大值时CQ也最大．‎ ‎【解】（1）当点P与点C关于AB对称时，CP⊥AB，设垂足为D．‎ ‎∵AB为⊙O的直径，∴∠ACB＝90°‎ ‎∴AB＝5，AC：CA＝4：3‎ ‎∴BC＝4，AC＝3‎ SRt△ACB＝AC·BC＝AB·CD ‎∴ ‎ ‎∵ 在Rt△ACB和Rt△PCQ中， ∠ACB＝∠PCQ＝90°，∠CAB＝∠CPQ ‎∴ Rt△ACB∽Rt△PCQ ‎∴ ‎ ‎∴ ‎ ‎（2）当点P运动到弧AB的中点时，过点B作BE⊥PC于点E（如图）．‎ ‎∵P是弧AB的中点，‎ 又∠CPB＝∠CAB ‎∴∠CPB＝ tan∠CAB＝ ‎ ‎∴ ‎ 从而 由（1）得，‎ ‎（3）点P在弧AB上运动时，恒有 故PC最大时，CQ取到最大值．‎ 当PC过圆心O，即PC取最大值5时，CQ 最大值为 ‎【说明】本题从点P在半圆AB上运动时的两个特殊位置的计算问题引申到求CQ的最大值，一方面渗透了“由特殊到一般”的思想方法，另一方面运用“运动变化”的观点解决问题时，寻求变化中的不变性（题中的Rt△ACB∽Rt△PCQ）往往是解题的关键．‎ ‎ 例5. 如图，PA，PB是⊙O的切线，A，B为切点，∠OAB＝30°．‎ ‎ （1）求∠APB的度数； ‎ ‎（2）当OA＝3时，求AP的长．‎ ‎ 【点评】本题用到的知识点较多，主要知识点有：①圆的切线的性质；②等腰三角形的性质；③四边形内角和定理；④垂径定理；⑤锐角三角函数等．‎ ‎【解】（1）∵在△ABO中，OA＝OB，∠OAB＝30°，‎ ‎∴∠AOB＝180°－2×30°＝120°，∵PA、PB是⊙O的切线，‎ ‎∴OA⊥PA，OB⊥PB，即∠OAP＝∠OBP＝90° ‎ ‎∴∠AOB+∠APB=180°‎ ‎∴∠APB=60°‎ ‎（2）如图，作OD⊥AB交AB于点D，‎ ‎∵在△OAB中，OA＝OB，∴AD＝AB，‎ ‎∵在Rt△AOD中，OA＝3，∠OAD＝30°，‎ ‎∴AD＝OA·cos30°＝，AP＝AB＝3‎ 例6. 如图，这是一个由圆柱体材料加工而成的零件，它是以圆柱体的上底面为底面，在其内部“掏取”一个与圆柱体等高的圆锥体而得到的，其底面直径AB＝12cm，高BC＝8cm，求这个零件的表面积．（结果保留根号）‎ ‎【解】这个零件的底面积＝×（）2＝36cm2 ‎ 这个零件的外侧面积＝12×8＝96cm2 圆锥母线长OC＝＝10cm ‎ 这个零件的内侧面积＝×12×10＝60cm2，‎ ‎∴这个零件的表面积为：36＋96＋60＝‎192‎cm2 ‎ 例7. 如图，O是圆柱形木块底面的圆心，过底面的一条弦AD，沿母线AB剖开，得剖面矩形ABCD，AD＝24cm，AB＝25cm，若AmD的长为底面周长的，如图所示：‎ ‎ （1）求⊙O的半径；‎ ‎ （2）求这个圆柱形木块的表面积．（结果可保留根号）‎ ‎【解】（1）连结OA、OD，作OE⊥AD于E，‎ 易知∠AOD＝120°，AE＝12cm，可得AO＝r＝＝8cm ‎ ‎（2）圆柱形木块的表面积＝2S圆＋S圆柱侧＝（384＋400）cm2‎ 例8. 在图1和图2中，已知OA＝OB，AB＝24，⊙O的直径为10. ‎ ‎ （1）如图1，AB与⊙O相切于点C，试求OA的值；‎ ‎（2）如图2，若AB与⊙O相交于D、E两点，且D、E均为AB的三等分点，试求tanA的值．‎ ‎（1）【解】连结OC，∵AB与⊙O相切于C点，‎ ‎∴∠OCA＝90°，∵OA＝OB，∴AC＝BC＝12 ‎ 在Rt△ACO中，OA＝＝13 ‎ ‎（2）作OF⊥AB于点F，连结OD，∴DF＝EF；AF＝AD＋DF＝8＋4＝12，‎ 在Rt△ODF中，OF＝＝3，‎ 在Rt△AOF中，tanA＝ ‎ 例9. 如图，在△ABC中，∠C＝90°，以BC上一点O为圆心，以OB为半径的圆交AB于点M，交BC于点N．‎ ‎ （1）求证：BA·BM＝BC·BN；‎ ‎（2）如果CM是⊙O的切线，N为OC的中点，当AC＝3时，求AB的值．‎ ‎（1）【证明】连接MN则∠BMN＝90°＝∠ACB，‎ ‎∴△ACB∽△NMB，∴，∴AB·BM＝BC·BN ‎ ‎（2）【解】连接OM，则∠OMC＝90°，‎ ‎∵N为OC中点，∴MN＝ON＝OM，∴∠MON＝60°，‎ ‎∵OM＝OB，∴∠B＝∠MON＝30°．‎ ‎∵∠ACB＝90°，∴AB＝‎2AC＝2×3＝6 ‎ 例10. 已知：如图，△ABC内接于⊙O，点D在OC的延长线上，sinB＝，∠CAD＝30°．‎ ‎ （1）求证：AD是⊙O的切线；（2）若OD⊥AB，BC＝5，求AD的长．‎ ‎（1）【证明】如图，连结OA，因为sinB＝，‎ 所以∠B＝30°，故∠O＝60°，又OA＝OC，‎ 所以△ACO是等边三角形， ‎ 故∠OAC＝60°，因为∠CAD＝30°，‎ 所以∠OAD＝90°，所以AD是⊙O的切线 ‎ ‎（2）【解】因为OD⊥AB，所以OC垂直平分AB，则AC＝BC＝5，‎ 所以OA＝5，在△OAD中，∠OAD＝90°，‎ 由正切定义，有tan∠AOD＝，所以AD＝5 ‎ 课后练习 一、填空题 ‎1. 已知扇形的圆心角为120°，半径为‎2cm，则扇形的弧长是_______cm，扇形的面积是________cm2．‎ ‎2. 如图，两个同心圆中，大圆的半径OA＝‎4cm，∠AOB＝∠BOC＝60°，则图中阴影部分的面积是______cm2．‎ ‎3. 圆锥的底面半径为‎6cm，高为‎8cm，那么这个圆锥的侧面积是_______cm2．‎ ‎4. 如图，⊙O的半径为‎4cm，直线l⊥OA，垂足为O，则直线l沿射线OA方向平移_____cm时与⊙O相切． ‎ ‎5. 两圆有多种位置关系，图中不存在的位置关系是______．‎ ‎6. 如图，从一块直径为a＋b的圆形纸板上挖去直径分别为a和b的两个圆，则剩下的纸板面积是_____．‎ ‎7. 如图，AB为半圆O的直径，CB是半圆O的切线，B是切点，AC交半圆O于点D，已知CD＝1，AD＝3，那么cos∠CAB＝________．‎ ‎8. 如图，BC为半⊙O的直径，点D是半圆上一点，过点D作⊙O的切线AD，BA⊥DA于A，BA交半圆于E，已知BC＝10，AD＝4，那么直线CE与以点O为圆心，为半径的圆的位置关系是______．‎ 二、选择题 ‎1. 在纸上剪下一个圆形和一个扇形的纸片，使之恰好能围成一个圆锥模型，若圆的半径为r，扇形的半径为R，扇形的圆心角等于120°，则r与R之间的关系是（ ）‎ ‎ A. R＝2r B. R＝r C. R＝3r D. R＝4r ‎2. 圆锥的底面半径为‎3cm，母线长为‎5cm，则它的侧面积是（ ）‎ ‎ A. ‎60‎cm2 B. ‎45‎cm‎2 C. ‎30‎cm2 D. ‎15‎cm2‎ ‎3. 已知圆锥侧面展开图的圆心角为90°，则该圆锥的底面半径与母线长的比为（ ）‎ ‎ A. 1：2 B. 2：‎1 C. 1：4 D. 4：1‎ ‎4. 将直径为‎64cm的圆形铁皮，做成四个相同圆锥容器的侧面（不浪费材料，不计接缝处的材料损耗），那么每个圆锥容器的高为（ ）‎ ‎ A. ‎8‎cm B. ‎8‎cm C. ‎16‎cm D. ‎‎16cm ‎5. 如图，圆心角都是90°的扇形OAB与扇形OCD叠放在一起，OA＝3，OC＝1，分别连结AC、BC，则圆中阴影部分的面积为（ ）‎ A. B. C. 2 D. 4‎ ‎6. 如图，将圆桶中的水倒入一个直径为‎40cm，高为‎55cm的圆口容器中，圆桶放置的角度与水平线的夹角为45°，若使容器中的水面与圆桶相接触，则容器中水的深度至少应为（ ）‎ ‎ A. ‎10cm B. ‎20cm C. ‎30cm D. ‎‎35cm ‎7. 生活处处皆学问，如图，眼镜镜片所在的两圆的位置关系是（ ）‎ A. 外离 B. 外切 C. 内含 D. 内切 ‎8. ⊙O的半径为4，圆心O到直线L的距离为3，则直线L与⊙O的位置关系是（ ）‎ ‎ A. 相交 B. 相切 C. 相离 D. 无法确定 ‎9. 如图，已知⊙O的直径AB与弦AC的夹角为35°，过点C的切线PC与AB的延长线交于点P，那么∠P等于（ ）‎ ‎ A. 15° B. 20° C. 25° D. 30°‎ ‎10. 已知圆A和圆B相切，两圆的圆心距为‎8cm，圆A的半径为‎3cm， 则圆B的半径是（ ）‎ ‎ A. ‎5cm B. ‎11cm C. ‎3cm D. ‎5cm或‎11cm ‎11. 如图PB为⊙O的切线，B为切点，连结PO交⊙O于点A，PA＝2，PO＝5，则PB的长度为（ ）‎ A. 4 B. C. 2 D. 4‎ ‎12. 如图，AB与⊙O切于点B，AO＝‎6cm，AB＝‎4cm，则⊙O的半径为（ ）‎ A. ‎4‎cm B. ‎2‎cm C. ‎2‎cm D. m 三、解答题 ‎1. 如图，已知正三角形ABC的边长为‎2a．‎ ‎ （1）求它的内切圆与外接圆组成的圆环的面积．‎ ‎ （2）根据计算结果，要求圆环的面积，只需测量哪一条弦的大小就可算出圆环的面积；‎ ‎ （3）将条件中的“正三角形”改为“正方形”“正六边形”，你能得出怎样的结论？‎ ‎ （4）已知正n边形的边长为‎2‎a，请写出它的内切圆与外接圆组成的圆环面积．‎ ‎2. 如图，已知O为原点，点A的坐标为（4，3），⊙A的半径为2. 过A作直线平行于轴，点P在直线上运动．‎ ‎（1）当点P在⊙A上时，请你直接写出它的坐标；‎ ‎（2）设点P的横坐标为12，试判断直线OP与⊙A的位置关系，并说明理由．‎ ‎3. 如图1，已知中，，．过点作，且，连接交于点．‎ ‎（1）求的长；‎ ‎（2）以点为圆心，为半径作⊙A，试判断与⊙A是否相切，并说明理由；‎ ‎（3）如图2，过点作，垂足为．以点为圆心，为半径作⊙A；以点为圆心，为半径作⊙C．若和的大小是可变化的，并且在变化过程中保持⊙A和⊙C相切，且使点在⊙A的内部，点在⊙A的外部，求和的变化范围．‎ ‎4. 已知：AB为⊙O的直径，P为AB弧的中点．‎ ‎（1）若⊙O′与⊙O外切于点P（见图甲），AP、BP的延长线分别交⊙O′于点C、D，连接CD，则△PCD是 三角形； ‎ （2）若⊙O′与⊙O相交于点P、Q（见图乙），连接AQ、BQ并延长分别交⊙O′于点E、F，请选择下列两个问题中的一个作答：‎ 问题一：判断△PEF的形状，并证明你的结论；‎ 问题二：判断线段AE与BF的关系，并证明你的结论． 我选择问题 ，结论： .‎ ‎5. 从卫生纸的包装纸上得到以下资料：两层300格，每格‎11.4cm×‎11cm，如图甲。用尺量出整卷卫生纸的半径（）与纸筒内芯的半径（），分别为‎5.8cm和‎2.3cm，如图乙。那么该两层卫生纸的厚度为多少cm？（π取3.14，结果精确到‎0.001cm）‎ ‎6. 设边长为‎2a的正方形的中心A在直线l上，它的一组对边垂直于直线l，半径为r的⊙O的圆心O在直线l上运动，点A、O间距离为D．‎ ‎（1）如图①，当r＜a时，根据d与a、r之间的关系，将⊙O与正方形的公共点的个数填入下表：‎ d、a、r之间的关系 公共点的个数 d＞a＋r d＝a＋r a－r＜d＜a＋r d＝a－r d＜a－r 所以，当r＜a时，⊙O与正方形的公共点的个数可能有　　　　　　　　　个；‎ ‎（2）如图②，当r＝a时，根据d与a、r之间的关系，将⊙O与正方形的公共点的个数填入下表：‎ d、a、r之间的关系 公共点的个数 d＞a＋r d＝a＋r a≤d＜a＋r d＜a 所以，当r＝a时，⊙O与正方形的公共点的个数可能有　　　　　　　　个；‎ ‎（3）如图③，当⊙O与正方形有5个公共点时，试说明r＝a；‎ ‎（4）就r＞a的情形，请你仿照“当……时，‎ ‎⊙O与正方形的公共点的个数可能有 个”的形式，至少给出一个关于“⊙O与正方形的公共点的个数”的正确结论．‎ 练习答案 一、填空题 ‎1. ， 2. 3. 60‎ ‎4. 4 5. 两圆相交 6. ‎ ‎7. 8. 相离 二、选择题 ‎1. C 2. D 3. C 4. A 5. C 6. D 7. A 8. A ‎ 9. B 10. D 11. A 12. B 三、解答题 ‎1. 解．（1）S圆环＝a2 ‎ ‎（2）弦AB或BC或AC ‎ ‎（3）圆环的面积均为·（）2. ‎ ‎（4）S圆环＝a2‎ ‎2. 解：⑴点P的坐标是（2，3）或（6，3） ‎ ⑵作AC⊥OP，C为垂足 ‎∵∠ACP＝∠OBP＝，∠1＝∠1‎ ‎∴△ACP∽△OBP ‎∴‎ 在中，‎ ‎，又AP＝12－4＝8， ∴‎ ‎∴AC＝≈1.94‎ ‎∵1.94<2‎ ‎∴OP与⊙A相交．‎ ‎3. 解：（1）在中，，‎ ‎．‎ ‎，．‎ ‎．‎ ‎，．‎ ‎（2）与⊙A 相切．‎ 在中，，，‎ ‎，．‎ 又，，‎ 与⊙A 相切．‎ ‎（3）因为，所以的变化范围为．‎ 当⊙A与⊙C 外切时，R＋r＝10，所以的变化范围为；‎ 当 ⊙A与⊙C 内切时，，所以的变化范围为．‎ ‎4. 证明：（1）等腰直角 ‎ ‎（2）问题一：△PEF是等腰直角三角形 ‎ 证明：连接PA、PB ‎ ‎∵AB是直径，∴∠AQB＝∠EQF＝90°‎ ‎∴EF是⊙O′的直径，∴∠EPF＝90° ‎ 在△APE和△BPF中：∵PA＝PB，∠PBF＝∠PAE ‎∠APE＝∠BPF＝90°＋∠EPB，∴△APE≌△BPF ‎∴PE＝PF，∴△PEF是等腰直角三角形 ‎ 问题二：参照问题一 ‎5. 解：设该两层卫生纸的厚度为xcm 则：11×11.4×x×300＝π（5.82－2.32）×11‎ x≈0.026‎ ‎ 答：该两层卫生纸的厚度约为‎0.026cm．‎ ‎6. （1）解：‎ d、a、r之间的关系 公共点的个数 D＞a＋r ‎0‎ d＝a＋r ‎1‎ a－r＜d＜a＋r ‎2‎ D＝a－r ‎1‎ D＜a－r ‎0‎ 所以，当r＜a时，⊙O与正方形的公共点的个数可能有0、1、2个； ‎ ‎（2）‎ d、a、r之间的关系 公共点的个数 d＞a＋r ‎0‎ d＝a＋r ‎1‎ a≤d＜a＋r ‎2‎ d＜a ‎4‎ 所以，当r＝a时，⊙O与正方形的公共点个数的可能有0、1、2、4个；‎ ‎（3）方法一：如图所示，连结OC．‎ 则OE＝OC＝r ，OF＝EF－OE＝2a－r． ‎ 在Rt△OCF中，由勾股定理得：OF2＋FC2＝OC2‎ 即（2a－r）2＋a2＝r2‎ ‎4a‎2－4ar＋r2＋a2＝r2‎ ‎5a‎2＝4ar ‎5a＝4r ‎∴r＝A．‎ 方法二：如图，连结BD、OE、BE、DE．‎ ‎∵四边形BCMN为正方形 ‎∴∠C＝∠M＝∠N＝90°‎ ‎∴BD为⊙O的直径，∠BED＝90°‎ ‎∴∠BEN＋∠DEM ＝90°‎ ‎∵∠BEN＋∠EBN＝90°‎ ‎∴∠DEM＝∠EBN ‎∴△BNE∽△EMD ‎ ‎∴‎ ‎∴DM＝a 由OE是梯形BDMN的中位线 得OE＝（BN＋MD）＝A．‎ ‎（4）①当a＜r＜时，⊙O与正方形的公共点的个数可能有0、1、2、4、6、7、8个；‎ ‎②当r＝a时，⊙O与正方形的公共点的个数可能有0、1、2、5、8个；‎ ‎③当时，⊙O与正方形的公共点的个数可能有0、1、2、3、4、6、8个；‎ ‎④当时，⊙O与正方形的公共点的个数可能有0、1、2、3、4个；‎ ‎⑤当时，⊙O与正方形的公共的点个数可能有0、1、2、3、4个．‎