中考数学试卷精选合辑60之5考试试题及答案 12页

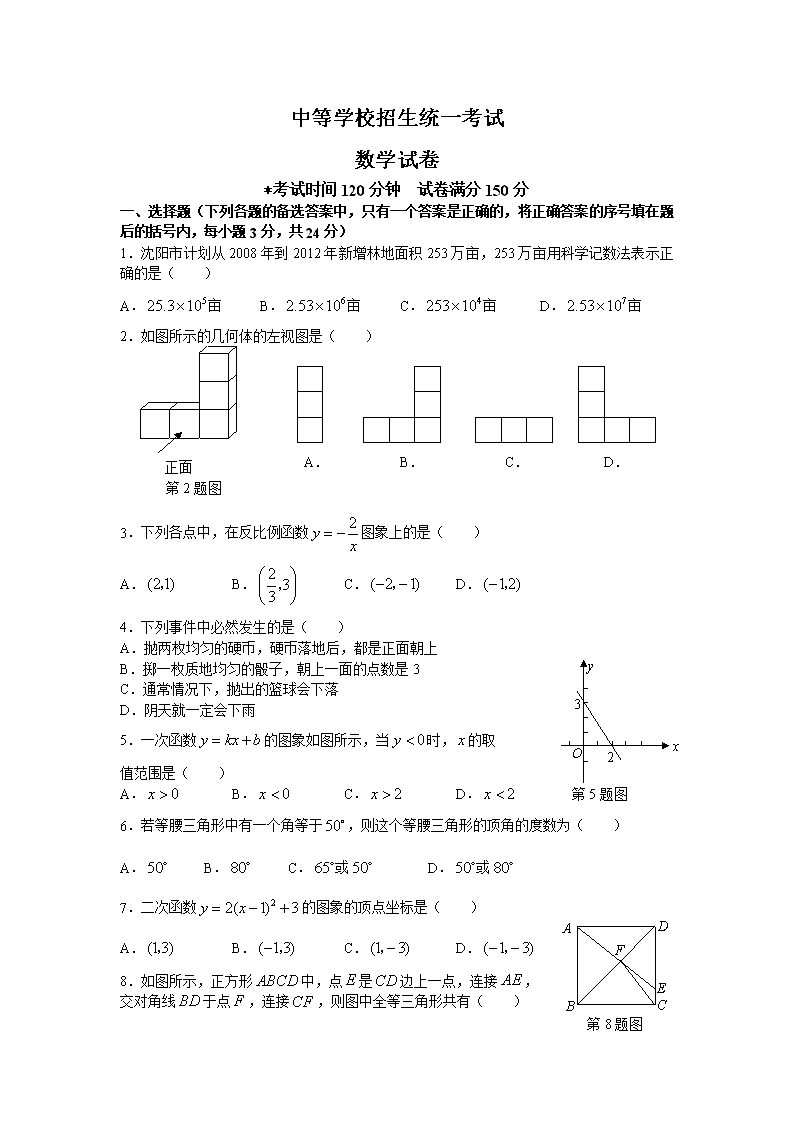
中等学校招生统一考试 数学试卷 ‎*考试时间120分钟 试卷满分150分 一、选择题（下列各题的备选答案中，只有一个答案是正确的，将正确答案的序号填在题后的括号内，每小题3分，共24分）‎ ‎1．沈阳市计划从2008年到2012年新增林地面积253万亩，253万亩用科学记数法表示正确的是（ ）‎ A．亩 B．亩 C．亩 D．亩 ‎2．如图所示的几何体的左视图是（ ）‎ 正面 第2题图 A．‎ B．‎ C．‎ D．‎ ‎3．下列各点中，在反比例函数图象上的是（ ）‎ A． B． C． D．‎ ‎4．下列事件中必然发生的是（ ）‎ ‎2‎ ‎3‎ 第5题图 y x O A．抛两枚均匀的硬币，硬币落地后，都是正面朝上 B．掷一枚质地均匀的骰子，朝上一面的点数是3‎ C．通常情况下，抛出的篮球会下落 D．阴天就一定会下雨 ‎5．一次函数的图象如图所示，当时，的取 值范围是（ ）‎ A． B． C． D．‎ ‎6．若等腰三角形中有一个角等于，则这个等腰三角形的顶角的度数为（ ）‎ A． B． C．或 D．或 A D C E F B 第8题图 ‎7．二次函数的图象的顶点坐标是（ ）‎ A． B． C． D．‎ ‎8．如图所示，正方形中，点是边上一点，连接，‎ 交对角线于点，连接，则图中全等三角形共有（ ）‎ A．1对 B．2对 C．3对 D．4对 二、填空题（每小题3分，共24分）‎ ‎9．已知与互余，若，则的度数为 ．‎ A D C B O 第12题图 ‎10．分解因式： ．‎ ‎11．已知中，，，的平分线交于点，‎ 则的度数为 ．‎ ‎12．如图所示，菱形中，对角线相交于点，若再补 充一个条件能使菱形成为正方形，则这个条件是 （只 B C D E A 第14题图 填一个条件即可）．‎ ‎13．不等式的解集为 ．‎ ‎14．如图所示，某河堤的横断面是梯形，，迎水坡 长‎13米，且，则河堤的高为 米．‎ ‎15．观察下列图形的构成规律，根据此规律，第8个图形中有 个圆．‎ 第1个 ‎……‎ 第2个 第3个 第4个 第15题图 ‎16．在平面直角坐标系中，点的坐标为，点的坐标为，点到直线的距离为，且是直角三角形，则满足条件的点有 个．‎ 三、（第17小题6分，第18，19小题各8分，第20小题10分，共32分）‎ ‎17．计算：．‎ ‎18．解分式方程：．‎ ‎19．先化简，再求值：‎ ‎，其中，．‎ ‎20．如图所示，在的方格纸中，每个小方格都是边长为1的正方形，我们称每个小正方形的顶点为格点，以格点为顶点的图形称为格点图形，如图①中的三角形是格点三角形．‎ ‎（1）请你在图①中画一条直线将格点三角形分割成两部分，将这两部分重新拼成两个不同的格点四边形，并将这两个格点四边形分别画在图②，图③中；‎ ‎（2）直接写出这两个格点四边形的周长．‎ 图①‎ 第20题图 图②‎ 图③‎ 四、（每小题10分，共20分）‎ ‎21．如图所示，是的一条弦，，垂足为，交于点，点在上．‎ E B D C A O 第21题图 ‎（1）若，求的度数；‎ ‎（2）若，，求的长．‎ ‎22．小刚和小明两位同学玩一种游戏．游戏规则为：两人各执“象、虎、鼠”三张牌，同时各出一张牌定胜负，其中象胜虎、虎胜鼠、鼠胜象，若两人所出牌相同，则为平局．例如，小刚出象牌，小明出虎牌，则小刚胜；又如，两人同时出象牌，则两人平局．‎ ‎（1）一次出牌小刚出“象”牌的概率是多少？‎ 小刚 小明 A1‎ B1‎ C1‎ A B C 第22题图 ‎（2）如果用分别表示小刚的象、虎、鼠三张牌，用，，分别表示小明的象、虎、鼠三张牌，那么一次出牌小刚胜小明的概率是多少？用列表法或画树状图（树形图）法加以说明．‎ 五、（本题12分）‎ ‎23．在学校组织的“喜迎奥运，知荣明耻，文明出行”的知识竞赛中，每班参加比赛的人数相同，成绩分为四个等级，其中相应等级的得分依次记为100分，90分，80分，70分，学校将某年级的一班和二班的成绩整理并绘制成如下的统计图：‎ A B C D 等级 第23题图 ‎12‎ ‎10‎ ‎8‎ ‎6‎ ‎4‎ ‎2‎ ‎0‎ 人数 ‎6‎ ‎12‎ ‎2‎ ‎5‎ 一班竞赛成绩统计图 二班竞赛成绩统计图 ‎16%‎ D级 ‎36%‎ C级 ‎44%‎ A级 B级4%‎ 请你根据以上提供的信息解答下列问题：‎ ‎（1）此次竞赛中二班成绩在级以上（包括级）的人数为 ；‎ ‎（2）请你将表格补充完整：‎ 平均数（分）‎ 中位数（分）‎ 众数（分）‎ 一班 ‎87.6‎ ‎90‎ 二班 ‎87.6‎ ‎100‎ ‎（3）请从下列不同角度对这次竞赛成绩的结果进行分析：‎ ‎①从平均数和中位数的角度来比较一班和二班的成绩；‎ ‎②从平均数和众数的角度来比较一班和二班的成绩；‎ ‎③从级以上（包括级）的人数的角度来比较一班和二班的成绩．‎ 六、（本题12分）‎ ‎24．一辆经营长途运输的货车在高速公路的处加满油后，以每小时80千米的速度匀速行驶，前往与处相距636千米的地，下表记录的是货车一次加满油后油箱内余油量（升）与行驶时间（时）之间的关系：‎ 行驶时间（时）‎ ‎0‎ ‎1‎ ‎2‎ ‎2.5‎ 余油量（升）‎ ‎100‎ ‎80‎ ‎60‎ ‎50‎ ‎（1）请你认真分析上表中所给的数据，用你学过的一次函数、反比例函数和二次函数中的一种来表示与之间的变化规律，说明选择这种函数的理由，并求出它的函数表达式；（不要求写出自变量的取值范围）‎ ‎（2）按照（1）中的变化规律，货车从处出发行驶4.2小时到达处，求此时油箱内余油多少升？‎ ‎（3）在（2）的前提下，处前方18千米的处有一加油站，根据实际经验此货车在行驶中油箱内至少保证有10升油，如果货车的速度和每小时的耗油量不变，那么在处至少加多少升油，才能使货车到达地．（货车在处加油过程中的时间和路程忽略不计）‎ 七、（本题12分）‎ ‎25．已知：如图①所示，在和中，，，，且点在一条直线上，连接分别为的中点．‎ ‎（1）求证：①；②是等腰三角形．‎ ‎（2）在图①的基础上，将绕点按顺时针方向旋转，其他条件不变，得到图②所示的图形．请直接写出（1）中的两个结论是否仍然成立；‎ ‎（3）在（2）的条件下，请你在图②中延长交线段于点．求证：．‎ C E N D A B M 图①‎ C A E M B D N 图②‎ 第25题图 八、（本题14分）‎ ‎26．如图所示，在平面直角坐标系中，矩形的边在轴的负半轴上，边在轴的正半轴上，且，，矩形绕点按顺时针方向旋转后得到矩形．点的对应点为点，点的对应点为点，点的对应点为点，抛物线过点．‎ ‎（1）判断点是否在轴上，并说明理由；‎ ‎（2）求抛物线的函数表达式；‎ y x O 第26题图 D E C F A B ‎（3）在轴的上方是否存在点，点，使以点为顶点的平行四边形的面积是矩形面积的2倍，且点在抛物线上，若存在，请求出点，点的坐标；若不存在，请说明理由．‎ ‎2008年沈阳市中等学校招生统一考试 数学试题参考答案及评分标准 一、选择题（每小题3分，共24分）‎ ‎1．B 2．A 3．D 4．C 5．C 6．D 7．A 8．C 二、填空题（每小题3分，共24分）‎ ‎9． 10． 11．‎ ‎12．（或，等） 13． 14．12‎ ‎15．65 16．8‎ 三、（第17小题6分，第18，19小题各8分，第20小题10分，共32分）‎ ‎17．解：原式 4分 ‎ 5分 ‎ 6分 ‎18．解： 2分 ‎ 5分 检验：将代入原方程，左边右边 7分 所以是原方程的根 8分 ‎（将代入最简公分母检验同样给分）‎ ‎19．解：原式 4分 ‎ 6分 当，时，‎ 原式 8分 ‎20．解：（1）答案不唯一，如分割线为三角形的三条中位线中任意一条所在的直线等．‎ ‎ 2分 拼接的图形不唯一，例如下面给出的三种情况：‎ 图①‎ 图②‎ 图③‎ 图④‎ 图⑤‎ 图⑥‎ 图⑦‎ 图⑧‎ 图⑨‎ 图①~图④，图⑤~图⑦，图⑧~图⑨，画出其中一组图中的两个图形． 6分 ‎（2）对应（1）中所给图①~图④的周长分别为，，，；‎ 图⑤~图⑦的周长分别为，，；‎ 图⑧~图⑨的周长分别为，．结果正确． 10分 四、（每小题10分，共20分）‎ ‎21．解：（1）， 3分 ‎ 5分 ‎（2），，为直角三角形，‎ ‎，，‎ 由勾股定理可得 8分 ‎ 10分 ‎22．解：（1） 4分 ‎（2）树状图（树形图）：‎ A1‎ B1‎ C1‎ A A1‎ B1‎ C1‎ B A1‎ B1‎ C1‎ C 开始 小刚 小明 ‎ 8分 或列表 小明 小刚 ‎ 8分 由树状图（树形图）或列表可知，可能出现的结果有9种，而且每种结果出现的可能性相同，其中小刚胜小明的结果有3种． 9分 ‎． 10分 五、（本题12分）‎ ‎23．解：（1）21 2分 ‎（2）一班众数为90，二班中位数为80 6分 ‎（3）①从平均数的角度看两班成绩一样，从中位数的角度看一班比二班的成绩好，所以一班成绩好； 8分 ‎②从平均数的角度看两班成绩一样，从众数的角度看二班比一班的成绩好，所以二班成绩好； 10分 ‎③从级以上（包括级）的人数的角度看，一班人数是18人，二班人数是12人，所以一班成绩好． 12分 六、（本题12分）‎ ‎24．解：（1）设与之间的关系为一次函数，其函数表达式为 1分 将，代入上式得，‎ ‎ 解得 ‎ 4分 验证：当时，，符合一次函数；‎ 当时，，也符合一次函数．‎ 可用一次函数表示其变化规律，‎ 而不用反比例函数、二次函数表示其变化规律． 5分 与之间的关系是一次函数，其函数表达式为 6分 ‎（2）当时，由可得 即货车行驶到处时油箱内余油16升． 8分 ‎（3）方法不唯一，如：‎ 方法一：由（1）得，货车行驶中每小时耗油20升， 9分 设在处至少加油升，货车才能到达地．‎ 依题意得，， 11分 解得，（升） 12分 方法二：由（1）得，货车行驶中每小时耗油20升， 9分 汽车行驶18千米的耗油量：（升）‎ 之间路程为：（千米）‎ 汽车行驶282千米的耗油量：‎ ‎（升） 11分 ‎（升） 12分 方法三：由（1）得，货车行驶中每小时耗油20升， 9分 设在处加油升，货车才能到达地．‎ 依题意得，，‎ 解得， 11分 在处至少加油升，货车才能到达地． 12分 七、（本题12分）‎ ‎25．证明：（1）①‎ ‎，‎ ‎ 3分 ‎②由得，‎ 分别是的中点， 4分 又 ‎，即为等腰三角形 6分 ‎（2）（1）中的两个结论仍然成立． 8分 ‎（3）在图②中正确画出线段 由（1）同理可证 又 ‎，和都是顶角相等的等腰三角形 10分 ‎，‎ ‎ 12分 八、（本题14分）‎ ‎26．解：（1）点在轴上 1分 理由如下：‎ 连接，如图所示，在中，，，‎ ‎，‎ 由题意可知：‎ 点在轴上，点在轴上． 3分 ‎（2）过点作轴于点 ‎，‎ 在中，，‎ 点在第一象限，‎ 点的坐标为 5分 由（1）知，点在轴的正半轴上 点的坐标为 点的坐标为 6分 抛物线经过点，‎ 由题意，将，代入中得 ‎ 解得 所求抛物线表达式为： 9分 ‎（3）存在符合条件的点，点． 10分 理由如下：矩形的面积 以为顶点的平行四边形面积为．‎ 由题意可知为此平行四边形一边，‎ 又 边上的高为2 11分 依题意设点的坐标为 点在抛物线上 解得，，‎ ‎，‎ 以为顶点的四边形是平行四边形，‎ y x O D E C F A B M ‎，，‎ 当点的坐标为时，‎ 点的坐标分别为，；‎ 当点的坐标为时，‎ 点的坐标分别为，． 14分 ‎（以上答案仅供参考，如有其它做法，可参照给分）‎