中考数学一轮复习 专题练习 数量和位置变化 浙教版 32页

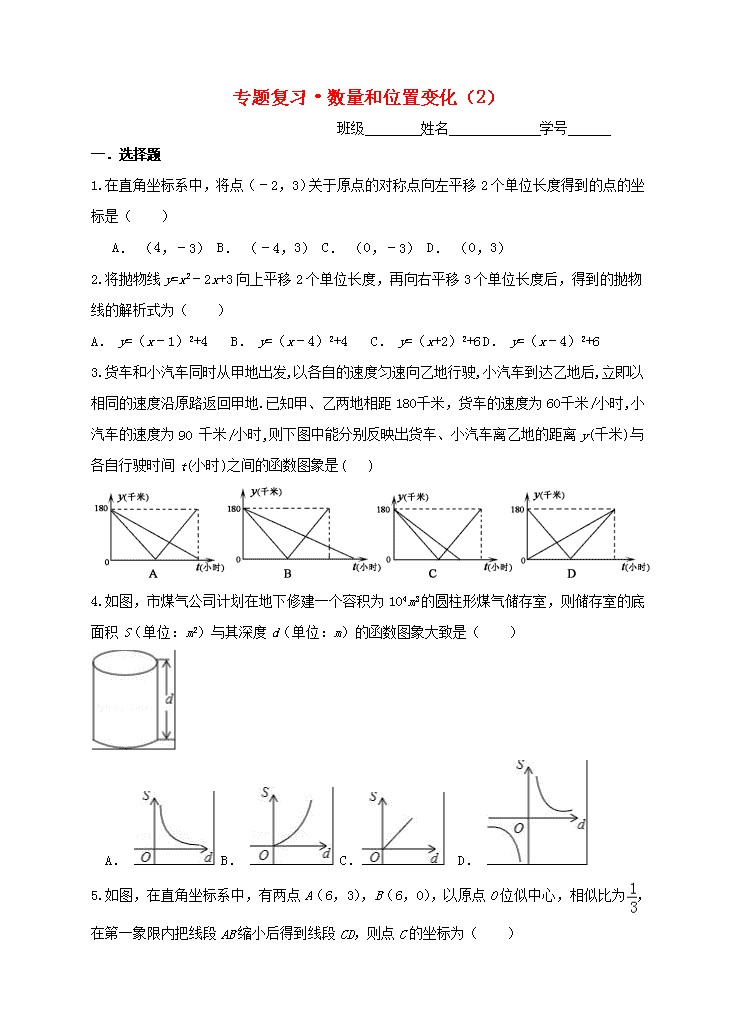
专题复习·数量和位置变化（2）‎ ‎ 班级 姓名 学号 ‎ 一．选择题 ‎1.在直角坐标系中，将点（﹣2，3）关于原点的对称点向左平移2个单位长度得到的点的坐标是（　　）‎ ‎　 A． （4，﹣3） B． （﹣4，3） C． （0，﹣3） D． （0，3）‎ ‎2.将抛物线y=x2﹣2x+3向上平移2个单位长度，再向右平移3个单位长度后，得到的抛物线的解析式为（　　）‎ A． y=（x﹣1）2+4 B． y=（x﹣4）2+4 C． y=（x+2）2+6 D． y=（x﹣4）2+6‎ ‎3.货车和小汽车同时从甲地出发,以各自的速度匀速向乙地行驶,小汽车到达乙地后,立即以相同的速度沿原路返回甲地.已知甲、乙两地相距180 千米，货车的速度为60 千米/小时,小汽车的速度为90 千米/小时,则下图中能分别反映出货车、小汽车离乙地的距离y(千米)与各自行驶时间t(小时)之间的函数图象是( )‎ ‎4.如图，市煤气公司计划在地下修建一个容积为104m3的圆柱形煤气储存室，则储存室的底面积S（单位：m2）与其深度d（单位：m）的函数图象大致是（　　）‎ ‎　A． B． C． D． ‎ ‎5.如图，在直角坐标系中，有两点A（6，3），B（6，0），以原点O位似中心，相似比为，在第一象限内把线段AB缩小后得到线段CD，则点C的坐标为（　　）‎ ‎　 A． （2，1） B． （2，0） C． （3，3） D． （3，1）‎ ‎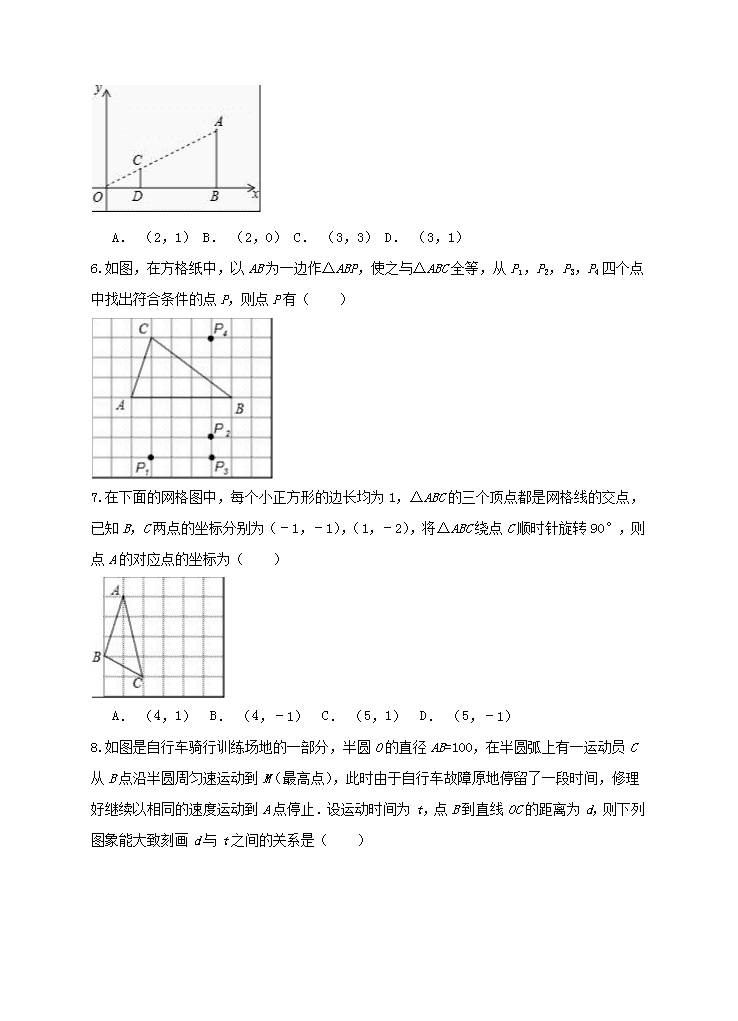6.如图，在方格纸中，以AB为一边作△ABP，使之与△ABC全等，从P1，P2，P3，P4四个点中找出符合条件的点P，则点P有（　　）‎ ‎7.在下面的网格图中，每个小正方形的边长均为1，△ABC的三个顶点都是网格线的交点，已知B，C两点的坐标分别为（﹣1，﹣1），（1，﹣2），将△ABC绕点C顺时针旋转90°，则点A的对应点的坐标为（　　）‎ ‎　 A． （4，1） B． （4，﹣1） C． （5，1） D． （5，﹣1）‎ ‎8.如图是自行车骑行训练场地的一部分，半圆O的直径AB=100，在半圆弧上有一运动员C从B点沿半圆周匀速运动到M（最高点），此时由于自行车故障原地停留了一段时间，修理好继续以相同的速度运动到A点停止．设运动时间为t，点B到直线OC的距离为d，则下列图象能大致刻画d与t之间的关系是（　　）‎ ‎9.如图，已知正△ABC的边长为2，E，F，G分别是AB，BC，CA上的点，且AE=BF=CG，设△EFG的面积为y，AE的长为x，则y关于x的函数图象大致是（ ）‎ A. B. C. D.‎ ‎10.如图，在平面直角坐标系xOy中，△由△绕点P旋转得到，则点P的坐标为（ ）‎ A. B. C. D. ‎ 二． 填空题 ‎11.在平面直角坐标系中，点A的坐标是，作点A关于x轴的对称点得到点A’，再作点A’关于y轴的对称点，得到点A’’，则点A’’的坐标是（ ， ）．‎ ‎12.如图是根据某公园的平面示意图建立的平面直角坐标系，公园的入口位于坐标原点O，古塔位于点A（400，300），从古塔出发沿射线OA方向前行300m是盆景园B，从盆景园B向左转90°后直行400m到达梅花阁C，则点C的坐标是 ．‎ ‎13.已知函数，那么＝ 。‎ ‎14.将正比例函数y=－6x的图象向上平移，则平移后所得图象对应的函数解析式可以是 .（写出一个即可）．‎ ‎15.函数的自变量的取值范围是 .‎ ‎16.已知抛物线，若点P（，5）与点Q关于该抛物线的对称轴对称，则点Q的坐标是 ．‎ ‎17.某水库的水位在5小时内持续上涨，初始水位高度为6米，水位以每小时0.3米的速度匀速上升， 则水库的水位与上涨时间之间的函数关系式是 .‎ ‎18.如果，，那么＝ ．‎ 三．解答题 ‎19.我们知道，函数的图像是由二次函数的图像向右平移m个单位，再向上平移n个单位得到.类似地，函数的图像是由反比例函数的图像向右平移m个单位，再向上平移n个单位得到，其对称中心坐标为（m，n）.‎ ‎ 理解应用 ‎ 函数的图像可以由函数的图像向右平移 个单位，再向上平移 个单位得到，其对称中心坐标为 ．‎ ‎ 灵活运用 ‎ 如图，在平面直角坐标系xOy中，请根据所给的的图像画出函数的图像，并根据该图像指出，当x在什么范围内变化时，？‎ 实际应用 ‎ 某老师对一位学生的学习情况进行跟踪研究.假设刚学完新知识时的记忆存留量为1.新知识学习后经过的时间为x，发现该生的记忆存留量随x变化的函数关系为；若在（≥4）时进行一次复习，发现他复习后的记忆存留量是复习前的2倍（复习时间忽略不计），且复习后的记忆存留量随x变化的函数关系为.如果记忆存留量为时是复习的“最佳时机点”，且他第一次复习是在“最佳时机点”进行的，那么当x为何值时，是他第二次复习的“最佳时机点”？‎ ‎20.如图，菱形OABC的顶点A的坐标为（2，0），∠COA＝600，将菱形OABC绕坐标原点O逆时针旋转1200得到菱形ODEF.‎ ‎（1）直接写出点F的坐标；‎ ‎（2）求线段OB的长及图中阴影部分的面积.‎ ‎21.平面直角坐标系中，点的横坐标的绝对值表示为，纵坐标 的绝对值表示为，我们把点的横坐标与纵坐标的绝对值之和叫做点的勾股值，记为：，即.（其中的“+”是四则运算中的加法）‎ ‎（1）求点,的勾股值、；‎ ‎（2）点在反比例函数的图像上，且，求点的坐标；‎ ‎（3）求满足条件的所有点围成的图形的面积.‎ ‎22.如图，在Rt△ABC中，∠ACB＝90°，AC=6，BC=8. 动点M从点A出发，以每秒1个单位长度的速度沿AB向点B匀速运动；同时，动点N从点B出发，以每秒3个单位长度的速度沿BA向点A匀速运动. 过线段MN的中点G作边AB的垂线，垂足为点G，交△ABC的另一边于点P，连接PM、PN，当点N运动到点A时，M、N两点同时停止运动，设运动时间为t秒.‎ ‎（1）当t＝ 秒时，动点M、N相遇；‎ ‎（2）设△PMN的面积为S，求S与t之间的函数关系式；‎ ‎（3）取线段PM的中点K，连接KA、KC，在整个运动过程中，△KAC的面积 是否变化？若变化，直接写出它的最大值和最小值；若不变化，请说明理由.‎ ‎23.如图，在平面直角坐标系中，已知点A（8，1），B（0，﹣3），反比例函数的图象经过点A，动直线x=t（0＜t＜8）与反比例函数的图象交于点M，与直线AB交于点N．‎ ‎（1）求k的值；‎ ‎（2）求△BMN面积的最大值；‎ ‎（3）若MA⊥AB，求t的值．‎ 二． 填空题 ‎11.在平面直角坐标系中，点A的坐标是，作点A关于x轴的对称点得到点A’，再作点A’关于y轴的对称点，得到点A’’，则点A’’的坐标是（ ， ）．‎ ‎12.如图是根据某公园的平面示意图建立的平面直角坐标系，公园的入口位于坐标原点O，古塔位于点A（400，300），从古塔出发沿射线OA方向前行300m是盆景园B，从盆景园B向左转90°后直行400m到达梅花阁C，则点C的坐标是 ．‎ ‎13.已知函数，那么＝ 。‎ ‎14.将正比例函数y=－6x的图象向上平移，则平移后所得图象对应的函数解析式可以是 .（写出一个即可）．‎ ‎15.函数的自变量的取值范围是 .‎ ‎16.已知抛物线，若点P（，5）与点Q关于该抛物线的对称轴对称，则点Q的坐标是 ．‎ ‎17.某水库的水位在5小时内持续上涨，初始水位高度为6米，水位以每小时0.3米的速度匀速上升， 则水库的水位与上涨时间之间的函数关系式是 .‎ ‎18.如果，，那么＝ ．‎ 三．解答题 ‎19.我们知道，函数的图像是由二次函数的图像向右平移m个单位，再向上平移n个单位得到.类似地，函数的图像是由反比例函数的图像向右平移m个单位，再向上平移n个单位得到，其对称中心坐标为（m，n）.‎ ‎ 理解应用 ‎ 函数的图像可以由函数的图像向右平移 个单位，再向上平移 个单位得到，其对称中心坐标为 ．‎ ‎ 灵活运用 ‎ 如图，在平面直角坐标系xOy中，请根据所给的的图像画出函数的图像，并根据该图像指出，当x在什么范围内变化时，？‎ 实际应用 ‎ 某老师对一位学生的学习情况进行跟踪研究.假设刚学完新知识时的记忆存留量为1.新知识学习后经过的时间为x，发现该生的记忆存留量随x变化的函数关系为；若在（≥4）时进行一次复习，发现他复习后的记忆存留量是复习前的2倍（复习时间忽略不计），且复习后的记忆存留量随x变化的函数关系为.如果记忆存留量为 时是复习的“最佳时机点”，且他第一次复习是在“最佳时机点”进行的，那么当x为何值时，是他第二次复习的“最佳时机点”？‎ ‎20.如图，菱形OABC的顶点A的坐标为（2，0），∠COA＝600，将菱形OABC绕坐标原点O逆时针旋转1200得到菱形ODEF.‎ ‎（1）直接写出点F的坐标；‎ ‎（2）求线段OB的长及图中阴影部分的面积.‎ ‎21.平面直角坐标系中，点的横坐标的绝对值表示为，纵坐标的绝对值表示为，我们把点的横坐标与纵坐标的绝对值之和叫做点的勾股值，记为：，即.（其中的“+”是四则运算中的加法）‎ ‎（1）求点,的勾股值、；‎ ‎（2）点在反比例函数的图像上，且，求点的坐标；‎ ‎（3）求满足条件的所有点围成的图形的面积.‎ ‎22.如图，在Rt△ABC中，∠ACB＝90°，AC=6，BC=8. 动点M从点A出发，以每秒1个单位长度的速度沿AB向点B匀速运动；同时，动点N从点B出发，以每秒3个单位长度的速度沿BA向点A匀速运动. 过线段MN的中点G作边AB的垂线，垂足为点G，交△ABC的另一边于点P，连接PM、PN，当点N运动到点A时，M、N两点同时停止运动，设运动时间为t秒.‎ ‎（1）当t＝ 秒时，动点M、N相遇；‎ ‎（2）设△PMN的面积为S，求S与t之间的函数关系式；‎ ‎（3）取线段PM的中点K，连接KA、KC，在整个运动过程中，△KAC的面积 是否变化？若变化，直接写出它的最大值和最小值；若不变化，请说明理由.‎ ‎23.如图，在平面直角坐标系中，已知点A（8，1），B（0，﹣3），反比例函数的图象经过点A，动直线x=t（0＜t＜8）与反比例函数的图象交于点M，与直线AB交于点N．‎ ‎（1）求k的值；‎ ‎（2）求△BMN面积的最大值；‎ ‎（3）若MA⊥AB，求t的值．‎ ‎24.如图，在平面直角坐标系xOy中，将抛物线的对称轴绕着点P（，2）顺时针旋转45°后与该抛物线交于A、B两点，点Q是该抛物线上的一点.‎ ‎（1）求直线AB的函数表达式；‎ ‎（2）如图①，若点Q在直线AB的下方，求点Q到直线AB的距离的最大值；‎ ‎（3）如图②，若点Q在y轴左侧，且点T（0，t）（t<2）是直线PO上一点，当以P、B、Q为顶点的三角形与△PAT相似时，求所有满足条件的t的值.‎ 答案详解 一．选择题 ‎3.货车和小汽车同时从甲地出发,以各自的速度匀速向乙地行驶,小汽车到达乙地后,立即以相同的速度沿原路返回甲地.已知甲、乙两地相距180 千米，货车的速度为60‎ ‎ 千米/小时,小汽车的速度为90 千米/小时,则下图中能分别反映出货车、小汽车离乙地的距离y(千米)与各自行驶时间t(小时)之间的函数图象是( )‎ 解答：解：由题意得 ‎ 出发前都距离乙地180 千米，出发两小时小汽车到达乙地距离变为零，再经过两小时小汽车又返回甲地距离又为180 千米，经过三小时，货车到达乙地距离变为零，‎ ‎ 故C 符合题意， ‎ ‎ 故选：C． ‎ ‎4.如图，市煤气公司计划在地下修建一个容积为104m3的圆柱形煤气储存室，则储存室的底面积S（单位：m2）与其深度d（单位：m）的函数图象大致是（　　）‎ 解答： 解：由储存室的体积公式知：104=Sd，‎ 故储存室的底面积S（m2）与其深度d（m）之间的函数关系式为S=（d＞0）为反比例函数．‎ 故选：A．‎ ‎5.如图，在直角坐标系中，有两点A（6，3），B（6，0），以原点O位似中心，相似比为，在第一象限内把线段AB缩小后得到线段CD，则点C的坐标为（　　）‎ ‎　 A． （2，1） B． （2，0） C． （3，3） D． （3，1）‎ 解：由题意得，△ODC∽△OBA，相似比是，‎ ‎∴=，又OB=6，AB=3，‎ ‎∴OD=2，CD=1，‎ ‎∴点C的坐标为：（2，1），‎ 故选：A．‎ ‎6.如图，在方格纸中，以AB为一边作△ABP，使之与△ABC全等，从P1，P2，P3，P4四个点中找出符合条件的点P，则点P有（　　）‎ ‎　 A． 1个 B． 2个 C． 3个 D． 4个 解答： 解：要使△ABP与△ABC全等，点P到AB的距离应该等于点C到AB的距离，即3个单位长度，故点P的位置可以是P1，P3，P4三个，‎ 故选C ‎7.在下面的网格图中，每个小正方形的边长均为1，△ABC的三个顶点都是网格线的交点，已知B，C两点的坐标分别为（﹣1，﹣1），（1，﹣2），将△ABC绕点C顺时针旋转90°，则点A的对应点的坐标为（　　）‎ ‎　 A． （4，1） B． （4，﹣1） C． （5，1） D． （5，﹣1）‎ 解答：解：如图，A点坐标为（0，2），‎ 将△ABC绕点C顺时针旋转90°，则点A的对应点的A′的坐标为（5，﹣1）．‎ ‎ 故选D．‎ ‎8.如图是自行车骑行训练场地的一部分，半圆O的直径AB=100，在半圆弧上有一运动员C从B点沿半圆周匀速运动到M（最高点），此时由于自行车故障原地停留了一段时间，修理好继续以相同的速度运动到A点停止．设运动时间为t，点B到直线OC的距离为d，则下列图象能大致刻画d与t之间的关系是（　　）‎ 故选C．‎ ‎9.如图，已知正△ABC的边长为2，E，F，G分别是AB，BC，CA上的点，且AE=BF=CG，设△EFG的面积为y，AE的长为x，则y关于x的函数图象大致是（ ）‎ A. B. C. D.‎ 解答： 解：根据题意，有AE=BF=CG，且正三角形ABC的边长为2，‎ ‎∴. ∴△AEG、△BEF、△CFG三个三角形全等．‎ 在△AEG中，，∴.‎ ‎∴．‎ ‎∴其图象为开口向上的二次函数.‎ 故选D.‎ ‎10.如图，在平面直角坐标系xOy中，△由△绕点P旋转得到，则点P的坐标为（ ）‎ A. B. C. D. ‎ 解答： 解：根据“旋转不改变图形的形状与大小”和“垂直平分线上的点到线段两端的距离相等”的性质，确定图形的旋转中心的步骤为：1.把这两个三角形的对应点连接起来；2.作每条线的垂直平分线；3.这三条垂直平分线交于一点,此点为旋转中心. 因此，‎ 作图如答图, 点P的坐标为.‎ 故选B.‎ 二． 填空题 ‎11.在平面直角坐标系中，点A的坐标是，作点A关于x 轴的对称点得到点A’，再作点A’关于y轴的对称点，得到点A’’，则点A’’的坐标是（ ， ）．‎ 解答： 解：关于x轴对称的点的坐标特征是横坐标相同，纵坐标互为相反数，从而点A关于x轴对称的点A’的坐标是；‎ 关于y轴对称的点的坐标特征是纵坐标不变，横坐标互为相反数，从而点A’ 关于y轴对称的点A’’的坐标是.‎ ‎12.如图是根据某公园的平面示意图建立的平面直角坐标系，公园的入口位于坐标原点O，古塔位于点A（400，300），从古塔出发沿射线OA方向前行300m是盆景园B，从盆景园B向左转90°后直行400m到达梅花阁C，则点C的坐标是 ．‎ 解答： 解：如答图，连接AC，‎ ‎∵A（400，300），∴OD=400m，AD=300m.‎ 由题意可得：AB=300m，BC=400m，‎ 在△AOD和△ACB中，∵，‎ ‎∴△AOD≌△ACB（SAS）.∴∠CAB=∠OAD.‎ ‎∵B、O在一条直线上，∴C、A、D也在一条直线上.‎ ‎∴AC=AO=500m， CD=AC=AD=800m.‎ ‎∴C点坐标为：（400，800）．‎ ‎13.已知函数，那么＝ 。‎ 解答： 解：把 直接代入函数即可求出函数值：‎ ‎ 。‎ ‎14.将正比例函数y=－6x的图象向上平移，则平移后所得图象对应的函数解析式可以是 .（写出一个即可）．‎ 解答： 解：根据“上加下减”的原则在函数解析式后加一个大于0的数即可，如y=－6x+1（答案不唯一）。‎ ‎15.函数的自变量的取值范围是 .‎ 解答： 解：求函数自变量的取值范围，就是求函数解析式有意义的条件，根据二次根式被开方数必须是非负数的条件，要使在实数范围内有意义，必须.‎ ‎16.已知抛物线，若点P（，5）与点Q关于该抛物线的对称轴对称，则点Q的坐标是 ．‎ 解答： 解：根据抛物线解析式求出抛物线对称轴为x，再根据图象得出点P（－2，5）关于对称轴对称点Q：两点的纵坐标不变，两点横坐标到对称轴的距离相等，都为3，得到Q点坐标为（4，5）。‎ ‎17.某水库的水位在5小时内持续上涨，初始水位高度为6米，水位以每小时0.3米的速度匀速上升， 则水库的水位与上涨时间之间的函数关系式是 .‎ 解答： 解：∵水位以每小时0.3米的速度匀速上升，上涨的时间是，‎ ‎∴上涨的水库的水位是.‎ ‎∵初始水位高度为6米，∴水库的水位.‎ ‎∵水库的水位在5小时内持续上涨，∴.‎ ‎∴水库的水位与上涨时间之间的函数关系式是.‎ ‎18.如果，，那么＝ ．‎ 解答： 解：根据函数值的意义得到关于的一元一次方程，解出即可：‎ 由题意可得：2=－4，化系数为1得：=－2。‎ 三．解答题 ‎19.我们知道，函数的图像是由二次函数的图像向右平移m个单位，再向上平移n个单位得到.类似地，函数的图像是由反比例函数的图像向右平移m个单位，再向上平移n个单位得到，其对称中心坐标为（m，n）.‎ ‎ 理解应用 ‎ 函数的图像可以由函数的图像向右平移 个单位，再向上平移 个单位得到，其对称中心坐标为 ．‎ ‎ 灵活运用 ‎ 如图，在平面直角坐标系xOy中，请根据所给的的图像画出函数的图像，并根据该图像指出，当x在什么范围内变化时，？‎ 实际应用 ‎ 某老师对一位学生的学习情况进行跟踪研究.假设刚学完新知识时的记忆存留量为1.新知识学习后经过的时间为x，发现该生的记忆存留量随x变化的函数关系为；若在（≥4）时进行一次复习，发现他复习后的记忆存留量是复习前的2倍（复习时间忽略不计），且复习后的记忆存留量随x变化的函数关系为.如果记忆存留量为时是复习的“最佳时机点”，且他第一次复习是在“最佳时机点”进行的，那么当x为何值时，是他第二次复习的“最佳时机点”？‎ ‎【答案】解：理解应用：1；1；（1，1）.‎ 灵活运用：函数的图像如答图：‎ 由图可知，当时，.‎ 实际应用：当时，，‎ ‎∴由解得.‎ ‎∴当进行第一次复习时，复习后的记忆存留量变为1.‎ ‎∴点（4，1）在函数的图象上.‎ ‎∴由解得.∴.‎ ‎∴由解得.‎ ‎∴当时，是他第二次复习的“最佳时机点”.‎ ‎20.如图，菱形OABC的顶点A的坐标为（2，0），∠COA＝600，将菱形OABC绕坐标原点O逆时针旋转1200得到菱形ODEF.‎ ‎（1）直接写出点F的坐标；‎ ‎（2）求线段OB的长及图中阴影部分的面积.‎ ‎【答案】解：（1）.‎ ‎（2）如答图，连接，与相交于点，‎ ‎∵菱形OABC中，，∠COA＝600，‎ ‎∴，，.‎ ‎∴，‎ ‎.‎ ‎∵将菱形OABC绕坐标原点O逆时针旋转1200得到菱形ODEF，‎ ‎∴.‎ ‎ ‎ ‎21.平面直角坐标系中，点的横坐标的绝对值表示为，纵坐标的绝对值表示为，我们把点的横坐标与纵坐标的绝对值之和叫做点的勾股值，记为：，即.（其中的“+”是四则运算中的加法）‎ ‎（1）求点,的勾股值、；‎ ‎（2）点在反比例函数的图像上，且，求点的坐标；‎ ‎（3）求满足条件的所有点围成的图形的面积.‎ ‎【答案】解：（1）∵,，‎ ‎∴，.‎ ‎（2）∵点在反比例函数的图像上，∴可设.‎ ‎∵，∴.‎ 若，则，解得.∴或.‎ 若，则，解得.∴或.‎ 综上所述，点的坐标为或或或.‎ ‎（3）设，‎ ‎∵，∴.‎ 若，则，即.‎ 若，则，即.‎ 若，则，即.‎ 若，则，即.‎ ‎∴满足条件的所有点围成的图形是正方形，如答图. ‎ ‎∴满足条件的所有点围成的图形的面积为18.‎ ‎22.如图，在Rt△ABC中，∠ACB＝90°，AC=6，BC=8. 动点M从点A 出发，以每秒1个单位长度的速度沿AB向点B匀速运动；同时，动点N从点B出发，以每秒3个单位长度的速度沿BA向点A匀速运动. 过线段MN的中点G作边AB的垂线，垂足为点G，交△ABC的另一边于点P，连接PM、PN，当点N运动到点A时，M、N两点同时停止运动，设运动时间为t秒.‎ ‎（1）当t＝ 秒时，动点M、N相遇；‎ ‎（2）设△PMN的面积为S，求S与t之间的函数关系式；‎ ‎（3）取线段PM的中点K，连接KA、KC，在整个运动过程中，△KAC的面积是否变化？若变化，直接写出它的最大值和最小值；若不变化，请说明理由.‎ ‎【答案】解：（1）2.5.‎ ‎（2）在整个运动过程中，分三段：点与点重合前；点与点重合后点M、N相遇前；点与点重合后点M、N相遇后.‎ 当点与点重合时，如答图1，‎ ‎∵，‎ ‎∴.‎ ‎∴根据勾股定理，得，解得.‎ 由（1）动点M、N相遇时，.‎ 当点N运动到点A时，由得.‎ ‎①当时，如题图，‎ ‎∵，∴.‎ ‎∵，，∴，即.‎ ‎∴.‎ ‎②当时，如答图2，‎ ‎∵，∴.‎ ‎∵，，‎ ‎∴，即.‎ ‎∴.‎ ‎③当时，如答图3，‎ ‎∵，∴.‎ ‎∵，，‎ ‎∴，即.‎ ‎∴.‎ 综上所述，S与t之间的函数关系式为.‎ ‎（3）在整个运动过程中，△KAC的面积变化，它的最大值是4，最小值是.‎ ‎23.如图，在平面直角坐标系中，已知点A（8，1），B（0，﹣3），反比例函数的图象经过点A，动直线x=t（0＜t＜8）与反比例函数的图象交于点M，与直线AB交于点N．‎ ‎（1）求k的值；‎ ‎（2）求△BMN面积的最大值；‎ ‎（3）若MA⊥AB，求t的值．‎ ‎【答案】解：（1）把点A（8，1）代入反比例函数得：k=1×8=8， ‎ ‎∴k=8.‎ ‎（2）设直线AB的解析式为：，‎ ‎∵A（8，1），B（0，﹣3），‎ ‎∴，解得：. ∴直线AB的解析式为：.‎ 由（1）得反比例函数的解析式为：，‎ 设，则.‎ ‎∴.‎ ‎∴△BMN的面积是t的二次函数.‎ ‎∵＜0，∴△BMN的面积有最大值.‎ ‎∴当t=3时，△BMN的面积的最大值为.‎ ‎（3）如答图，过点作轴于点，延长交轴于点，‎ ‎∵MA⊥AB，∴.‎ ‎∴，即，解得.‎ ‎∴.‎ 又∵A（8，1），∴直线AP的解析式为：.‎ ‎∴解得，.‎ ‎∴.‎ ‎24.如图，在平面直角坐标系xOy中，将抛物线的对称轴绕着点P（，2）顺时针旋转45°后与该抛物线交于A、B两点，点Q是该抛物线上的一点.‎ ‎（1）求直线AB的函数表达式；‎ ‎（2）如图①，若点Q在直线AB的下方，求点Q到直线AB的距离的最大值；‎ ‎（3）如图②，若点Q在y轴左侧，且点T（0，t）（t<2）是直线PO上一点，当以P、B、Q为顶点的三角形与△PAT相似时，求所有满足条件的t的值.‎ ‎【答案】解：（1）如答图1，设直线AB与轴的交点为M，‎ ‎∵，P（，2），∴.‎ 设直线AB的解析式为，‎ 则，解得.‎ ‎∴直线AB的解析式为.‎ ‎（2）如答图2，过点Q作轴的垂线QC，交AB于点C，再过点Q作直线AB的垂线，垂足为点D，‎ 根据条件可知，是等腰直角三角形.‎ ‎∴.‎ 设，则，‎ ‎∴.‎ ‎∴.‎ ‎∴当时，点Q到直线AB的距离的最大值为.‎ ‎（3）∵，∴中必有一角等于45°.‎ ‎①由图可知，不合题意.‎ ‎②若，‎ 如答图3，过点B作轴的平行线与轴和抛物线分别交于点，此时，.‎ 根据抛物线的轴对称性质，知，‎ ‎∴是等腰直角三角形.‎ ‎∵与相似，且，‎ ‎∴也是等腰直角三角形.‎ i）若，‎ 联立，解得或.‎ ‎∴. ∴.∴，此时，.‎ ii）若，，此时，.‎ ‎③若，②是情况之一，答案同上.‎ 如答图4，5，过点B作轴的平行线与轴和抛物线分别交于点，以点为圆心，为半径画圆，则都在上，设与y轴左侧的抛物线交于另一点.‎ ‎∵根据圆周角定理，，‎ ‎∴点也符合要求.‎ 设，‎ 由得解得或，‎ 而，故.∴.‎ 可证是等边三角形，∴.‎ ‎∴.‎ 则在中，.‎ i）若，‎ 如答图4，过点作轴于点，‎ 则，‎ ‎∴.‎ ‎∴，此时，.‎ ii）若，‎ 如答图5，过点作轴于点，‎ 设，则.‎ ‎∵，∴，.∴.‎ ‎∴，此时，.‎ 综上所述，所有满足条件的t的值为或或或.‎