中考数学模拟试题含答案 7页

2011 年中考数学模拟试题<二> 一、填空题（每题 3 分，共 30 分） 1．已知一元二次方程 ax2+x-b=0 的一根为 1，则 a-b 的值是____________. 2、写出一个无理数使它与 32  的积是有理数 3. 在 2 ， 12 ， 22 ， 32 中任取其中两个数相乘．积为有理数的概率为 。 4．直线y=x+3上有一点P(m-5，2m)，则P点关于原点的对称点P′为______． 5．若式子 x x1 有意义，则x的取值范围是 ． 6．计算： 2 2 2  = . 7、如图同心圆，大⊙O 的弦 AB 切小⊙O 于 P， 且 AB=6，则圆环的面积为 。 8．如图，P 是射线 y＝ 5 3 x(x＞0)上的一点，以 P 为 圆心的圆与 y 轴相切于 C 点，与 x 轴的正半轴交于 A、B 两点，若⊙P 的半径为 5，则 A 点坐标是_________； 9．在半径为 2 的⊙O 中，弦 AB 的长为 2，则弦 AB 所对的圆周角的度数 为 。 10、如图，在△ABC 中，BC＝4，以点 A 为圆心，2 为半径的⊙A 与 BC 相切于点 D，交 AB 于 E，交 AC 于 F，点 P 是⊙A 上的一点， 且∠EPF＝40°，则图中阴影部分的面积是__________（结果保留 ） 二、选择题（每题 3 分，共 15 分） 11. 下列成语所描述的事件是必然发生的是（ ）. A. 水中捞月 B. 拔苗助长 C. 守株待免 D. 瓮中捉鳖 12．如图，点 A、C、B 在⊙O 上，已知∠AOB =∠ACB = a. 则 a 的值为（ ）. A. 135° B. 120° C. 110° D. 100° 13．圆心在原点 O，半径为 5 的⊙O，则点 P（-3，4）与⊙O 的位置关系是（ ）. A. 在 OO 内 B. 在 OO 上 C. 在 OO 外 D. 不能确定 14、已知两圆的半径是方程 01272  xx 两实数根，圆心距为 8，那么这两个 圆的位置关系是（ ） A.内切 B.相交 C.外离 D.外切 15.一个均匀的立方体骰子六个面上标有数 1，2，3，4，5，6，若以连续掷两次 骰子得到的数 m n和 作为点 P 的坐标，则点 P 落在反比例函数 6y x  图象与坐标轴 O C BA o p A B A B P x y C O x5 3y  所围成区域内（含落在此反比例函数的图象上的点）的概率是（ ） A. 1 8 B. 2 9 C. 11 18 D. 7 18 三、解答题（共 4 小题，第 16.，17 小题 6 分，第 18、19 小题 7 分） 16.计算： 12 - 1 3 3       + )13(3  - 2008 0 - 23  17．已知 a、b、c 均为实数，且 2a +︳b+1︳+  23c =0 求方程 02  cbxax 的根。 18 ． 已 知 a 、 b 、 c 是 三 角 形 的 三 条 边 长 ， 且 关 于 x 的 方 程 0)()(2)( 2  baxabxbc 有两个相等的实数根，试判断三角形的形状 19、在一次晚会上，大家围着飞镖游戏前。只见靶子设计成如图形式．已知从里 到外的三个圆的半径分别为 l，2。3，并且形成 A，B，C 三个区域．如果飞 镖没有停落在最大圆内或只停落在圆周上，那么可以重新投镖． (1)分别求出三个区域的面积； (2)雨薇与方冉约定：飞镖停落在 A、B 区域雨薇得 1 分，飞镖落在 C 区域方冉 得 1 分．你认为这个游戏公平吗? 为什么? 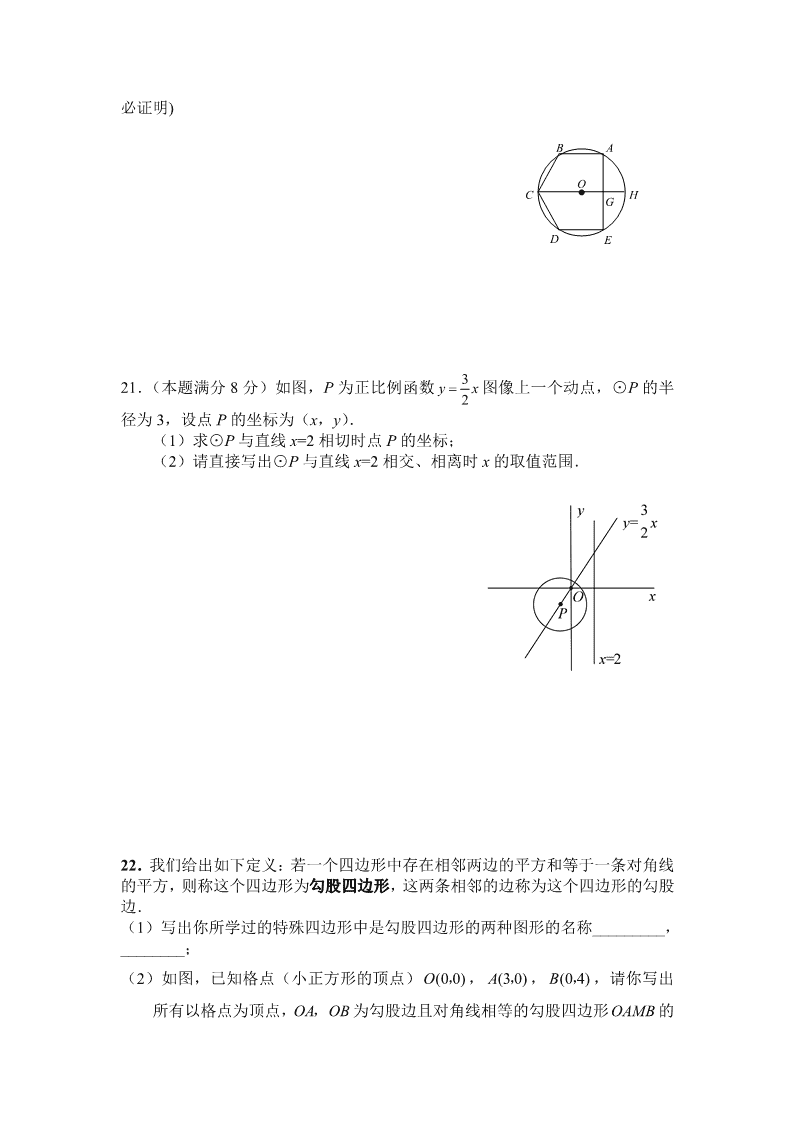如果不公平，请你修改得分规则，使 这个游戏公平． 20．如图。⊙O 上有 A、B、C、D、E 五点，且已知 AB = BC = CD = DE，AB∥ ED． (1)求∠A、∠E 的度数； (2)连 CO 交 AE 于 G。交AE⌒ 于 H，写出四条与直径 CH 有关的正确结论．(不 CBA 必证明) 21．（本题满分 8 分）如图，P 为正比例函数 3 2y x 图像上一个动点，⊙P 的半 径为 3，设点 P 的坐标为（x，y）． （1）求⊙P 与直线 x=2 相切时点 P 的坐标； （2）请直接写出⊙P 与直线 x=2 相交、相离时 x 的取值范围． 22．我们给出如下定义：若一个四边形中存在相邻两边的平方和等于一条对角线 的平方，则称这个四边形为勾股四边形，这两条相邻的边称为这个四边形的勾股 边． （1）写出你所学过的特殊四边形中是勾股四边形的两种图形的名称_________， ________； （2）如图，已知格点（小正方形的顶点） (0 0)O ， ， (3 0)A ， ， (0 4)B ， ，请你写出 所有以格点为顶点，OA OB， 为勾股边且对角线相等的勾股四边形OAMB 的 HG E O D C B A 顶点 M 的坐标； （3）如图，将 ABC△ 绕顶点 B 按顺时针方向旋转 60 ，得到 DBE△ ，连结 AD DC， ， 30DCB  ∠ ．求证： 2 2 2DC BC AC  ，即四边形 ABCD 是勾股 四边形． 25.如图 1,在平面直角坐标系中,以坐标原点 O 为圆心的⊙O 的半径为 2 －1,直 线 l: y=－X－ 2 与坐标轴分别交于 A,C 两点,点 B 的坐标为(4,1) ,⊙B 与 X 轴 相切于点 M.。 (1)求点 A 的坐标及∠CAO 的度数; (2) ⊙B 以每秒 1 个单位长度的速度沿 X 轴负方向平移,同时,直线 l 绕点 A 顺时 针匀速旋转.当⊙B 第一次与⊙O 相切时,直线 l 也恰好与⊙B 第一次相切.问:直线 AC 绕点 A 每秒旋转多少度? (3)如图 2.过 A,O,C 三点作⊙O1 ,点 E 是劣弧AO⌒ 上一点,连接 EC,EA.EO,当点 E 在劣弧AO⌒ 上运动时(不与 A,O 两点重合), EO EAEC  的值是否发生变化?如果不变, 求其值,如果变化,说明理由. . y B O A x A B C D E 60 X Y A O E O1 图 2 C C A l O x B M 图 1 2011 年中考数学模拟试题<二>答案 一填空题： （1）、—1 （2）、如 2 — 3 不唯一 （3）、 6 1 （4）、 （7，4） （5）、X≥—1 且 X≠0 （6）、 2 +1 （7）、 9 （8）、 （1，0） （9）、 300 或 1500 （10）、4— 9 8π 二、选择题 11、 D 12、B 13、B 14、C 15、 D 16、A 三、解答题： 17．解：原式=2 3 — 3 +3— 3 —1+ 3 —2 …….算对每项 1 分，共 5 分 = 3 ………… ……………6 分 18、解：a = 2 b = —1 c = —3 ................... 3 分 2X2—X—3=0 ( 2X—3)(X+1)=0 ......................... 6 分 X1= 2 3 X2= —1 ...................... 7 分 19、解：由已知条件得   0))((4)(2 2  babcab ...............2 分 整理为 0))((  caba ........................................................5 分 ∴ caba  或 ............................................... 6 分 ∵ bcbc  则0 ∴ 这个三角形是等腰三角形． ............................ 7 分 20.解：(1)SA=π·12=π,SB=π·22-π·12=3π,SC=π·32-π·22=5π ……3 分 (2)P(A)= π9 π = 9 1 ,P(B)= π9 3π = 9 3 ,P(C)= π9 5π = 9 5 …………………4 分 P(雨薇得分)= 9 1 ×1+ 9 3 ×1= 9 4 ,P(方冉得分)= 9 5 ×1= 9 5 ……………5 分 ∵P(雨薇得分)≠P(方冉得分) ∴这个游戏不公平. …………………6 分 修改得分规则：飞镖停落在 A 区域得 2 分，飞镖停落在 B 区域、C 区域得 1 分， 这样游戏就公平了. …………………8 分 21．解：(1)∵AB=BC=CD=DE ∴ ⌒ AB= ⌒ BC= ⌒ CD= ⌒ DE ∴ ⌒BCDE= ⌒ABCD ………2 分 ∴∠A=∠E ………3 分 又∵AB∥ED ∴∠A+∠E=180° ∴∠A=∠E=90° ………4 分 (2) ①CH 平分∠BCD ②CH∥BA ③CH∥DE ④CH⊥AE ⑤ ⌒ AH= ⌒ EH⑥AG=EG 等(写出其中 4 条即可，每条 1 分) …8 分 22、解： (1).P1 (—1, -- 2 3 ) P2(5, 2 15 ) ...................4 分 (2).相交 -- 2 3 ＜X＜ 2 15 ...........................................6 分 相离 -- 2 3 ＞ 2 15 或 X＜—1 ........ 8 分 23、解：(1).D(2, 0) ............................................ 2 分 (2).R=2 5 …………................ 1 分 圆心角度 900 ............2 分 (3).r= 2 5 ................................4 分 24、解： (1).长方形 .,正方形........................................... 2 分 (2). M1(3, 4) M2(4, 3) …………................ 4 分 (3).证明:;连结 EC ……………………5 分 ∵⊿ABC≌⊿DBE ………6 分 ∴BC=BE AC=DE 又∵∠CBE=600 ∴⊿CBE 是等边三角形 ………7 分 ∴∠BCE=600 BC=EC 又∵∠DCB=300 ∴∠BCE+∠DCB=900 即∠DCE=900 ........8 分 DC2+EC2=AC2 2 2 2DC BC AC  ..... ...9 分 25、解：（1）、A（－ 2 ，0） ∵C（0，－ 2 ），∴OA=OC。 ∵OA⊥OC ∴∠CAO=450 （2）如图，设⊙B 平移 t 秒到⊙B1 处与⊙O 第一次相切，此时，直线 l 旋转到 l’ 恰好与⊙B1 第一次相切于点 P, ⊙B1 与 X 轴相切于点 N, 连接 B1O,B1N,则 MN=t, OB1= 2 B1N⊥AN ∴MN=3 即 t=3 连接 B1A, B1P 则 B1P⊥AP B1P = B1N ∴∠PA B1=∠NAB1 ∵OA= OB1= 2 ∴∠A B1O=∠NAB1 ∴∠PA B1=∠A B1O ∴PA∥B1O 在 Rt⊿NOB1 中,∠B1ON=450, ∴∠PAN=450, ∴∠1= 900. ∴直线 AC 绕点 A 平均每秒 300. (3). EO EAEC  的值不变,等于 2 ,,,如图在 CE 上截取 CK=EA,连接 OK, ∵∠OAE=∠OCK, OA=OC ∴⊿OAE≌⊿OCK, ∴OE=OK ∠EOA=∠KOC ∴∠EOK=∠AOC= 900. ∴EK= 2 EO , ∴ EO EAEC  = 2 1 N C A l O x B M 图 1 B1 P l’ X Y A O E O1 图 2 C K