中考数学圆与圆的位置关系押轴题专练 5页

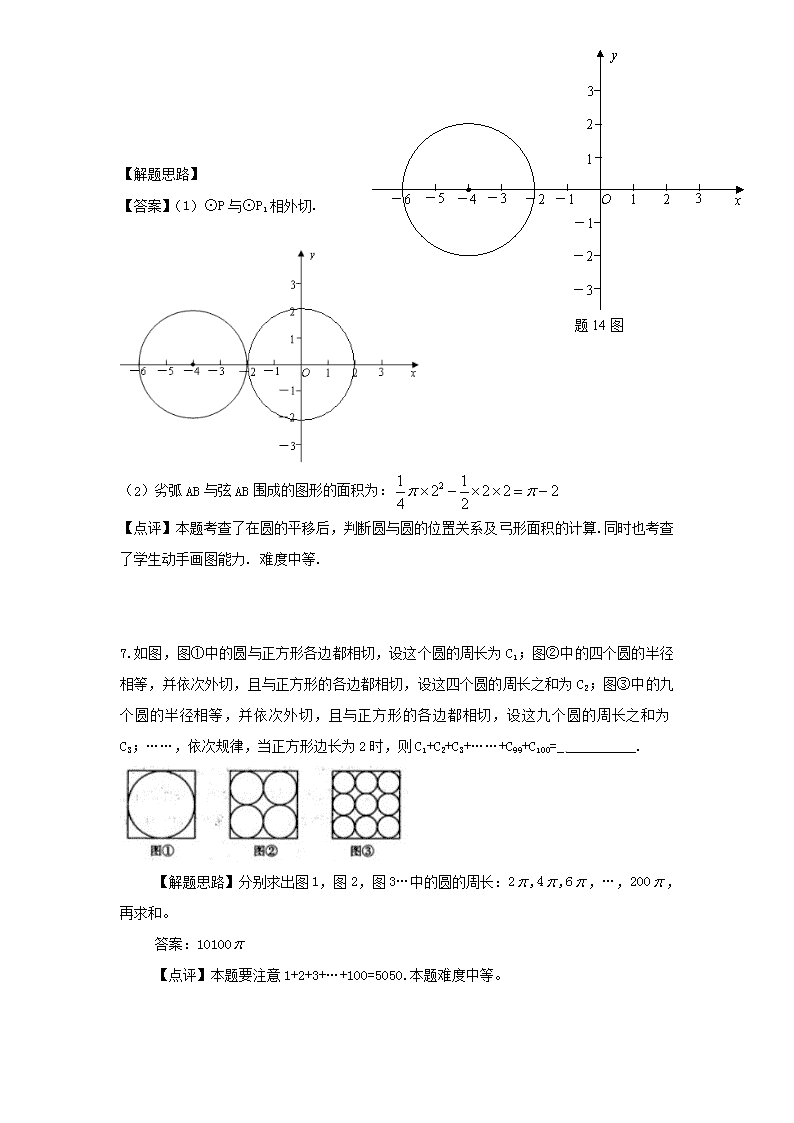
‎ 圆与圆的位置关系 ‎1．已知⊙O1与⊙O2的半径分别为3㎝和4㎝，若O1O2=7㎝，则⊙O1与⊙O2的位置关系是 A．相交 B．相离 C．内切 D．外切 ‎【解题思路】：当圆心距等于半径和时，两圆外切。‎ ‎【答案】：D ‎【点评】：本题考察了两圆圆心距同其半径和（差）的大小比较与两圆位置特点的关系。难度较小。‎ ‎2．如图，在Rt△ABC中，∠ABC = 90, AB = ‎8cm , BC = ‎6cm , 分别以A,C为圆心，以 的长为半径作圆, 将 Rt△ABC截去两个扇形，则剩余（阴影）部分的面积为 cm（结果保留π）‎ ‎【解题思路】求不规则图形的面积则转换为规则图形面积的和差，图中阴影部分面积等于△ABC与两扇形面积的差，则为：（π）π ‎【答案】π．‎ ‎【点评】本题主要考查了勾股定理、扇形面积公式及转化和整体思想，学生在求解两扇形的面积和时不宜想到两者和即个圆面积.难度较大.‎ ‎3．如图，半径为1的小圆在半径为 9 的大圆内滚动，且始终与大圆相切，则小圆扫过的阴影部分的面积为（ ）‎ A．17 B．‎32‎ C．49 D．80 ‎ ‎【解题思路】小圆扫过的阴影部分是圆环，S大=πR2=π×92=91π，S大=πr2=π×(9－2)2=49π，所以小圆扫过的阴影部分的面积为：91π－49π=32π．‎ ‎【答案】B．‎ ‎【点拨】本题考查了圆的面积公式和相切两圆的性质．解决此类不规则阴影部分面积的方法就是把这些不规则图形转化为规则图形的进行求解．难度较小．‎ ‎4．已知⊙O1与⊙O2的半径、分别是方程 的两实根，若⊙O1与⊙O2的圆心距=5．则⊙O1与⊙O2的位置关系是____ ‎ ‎【解题思路】由题知，、分别是方程 的两实根，解得，，故所以两圆相交。‎ ‎【答案】相交 ‎【点评】本题将一元二次方程和圆和圆的位置关系结合考察是一道较好的题目，难度中等 ‎5‎ （a，0）‎ x y O ‎·‎ ‎3‎ ‎5‎ 第17题图 ．如图，小圆的圆心在原点，半径为3，大圆的圆心坐标为（a，0），半径为5．如果两圆内含，那么a的取值范围是________.‎ ‎【解题思路】因为小圆圆心为原点，大圆的圆心坐标为(a，0)，所以圆心距为a，由两圆位置为内含得数量关系：3-5＜a＜5-3，即：－2