中考数学选择填空难题精选 31页

全国各地各地中考数学选择、填空难题精选（一）‎ ‎1、（2013济南）函数y=x2+bx+c与y=x的图象如图所示，有以下结论：‎ ‎①b2﹣4c＞0；②b+c+1=0；③3b+c+6=0；④当1＜x＜3时，x2+（b﹣1）x+c＜0．‎ 其中正确的个数为（　B　）‎ ‎　‎ A．‎ ‎1‎ B．‎ ‎2‎ C．‎ ‎3‎ D．‎ ‎4‎ ‎2、（2013济南）一项“过关游戏”规定：在过第n关时要将一颗质地均匀的骰子（六个面上分别刻有1到6的点数）抛掷n次，若n次抛掷所出现的点数之和大于n2，则算过关；否则不算过关，则能过第二关的概率是（　A　）‎ ‎　‎ A．‎ B．‎ C．‎ D．‎ ‎3、（2013鄂州）小轩从如图所示的二次函数y = ax2＋bx＋c（a≠0）的图象中，‎ 观察得出了下面五条信息：①ab > 0 ②a＋b＋c < 0 ‎ ‎③b＋2c > 0 ④a－2b＋4c > 0 ⑤.‎ 你认为其中正确信息的个数有（ D ）‎ ‎ A．2个 B．3个 C．4个 D．5个 ‎4、（2013鄂州）如图，已知直线a//b，且a与b之间的距离为4，点A到直线a的距离为2，点B到直线b的距离为3，AB=.试在直线a上找一点M，在直线b上找一点N，满足MN⊥a且AM+MN+NB的长度和最短，则此时AM+NB=（ B ）‎ A．6 B．8 C．10 D．12‎ ‎5、（2013荆门）设，是方程的两实数根，则 2014 .‎ ‎6、（2013荆门）若抛物线与x轴只有一个交点，且过点，.则 9 .‎ ‎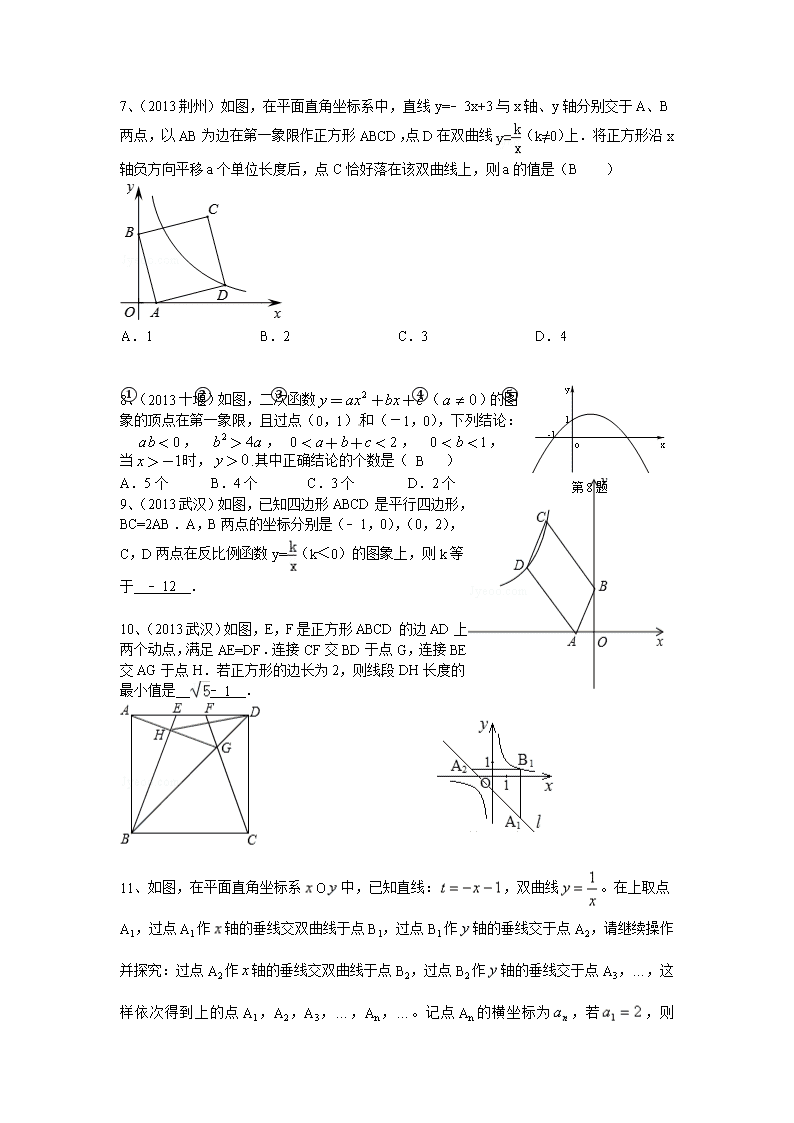7、（2013荆州）如图，在平面直角坐标系中，直线y=﹣3x+3与x轴、y轴分别交于A、B两点，以AB为边在第一象限作正方形ABCD，点D在双曲线（k≠0）上．将正方形沿x轴负方向平移a个单位长度后，点C恰好落在该双曲线上，则a的值是（B　　）‎ ‎　‎ A．‎ ‎1‎ B．‎ ‎2‎ C．‎ ‎3‎ D．‎ ‎4‎ 第8题 ‎8、（2013十堰）如图，二次函数（）的图象的顶点在第一象限，且过点（0，1）和（－1，0），下列结论：①，②，③，④，⑤当时，.其中正确结论的个数是（ B ）‎ A．5个 B．4个 C．3个 　　 D．2个 ‎9、（2013武汉）如图，已知四边形ABCD是平行四边形，BC=2AB．A，B两点的坐标分别是（﹣1，0），（0，2），C，D两点在反比例函数y=（k＜0）的图象上，则k等于　﹣12　．‎ ‎10、（2013武汉）如图，E，F是正方形ABCD的边AD上两个动点，满足AE=DF．连接CF交BD于点G，连接BE交AG于点H．若正方形的边长为2，则线段DH长度的最小值是　﹣1　．‎ ‎11、如图，在平面直角坐标系O中，已知直线：，双曲线。在上取点A1，过点A1作轴的垂线交双曲线于点B1，过点B1作轴的垂线交于点A2，请继续操作并探究：过点A2作轴的垂线交双曲线于点B2，过点B2作轴的垂线交于点A3，…，这样依次得到上的点A1，A2，A3，…，An，…。记点An的横坐标为，若，则 ‎=__________，=__________；若要将上述操作无限次地进行下去，则不能取的值是__________‎ 答案：；；。‎ ‎12、（2013兰州）如图，以扇形OAB的顶点O为原点，半径OB所在的直线为x轴，建立平面直角坐标系，点B的坐标为（2，0），若抛物线y=x2+k与扇形OAB的边界总有两个公共点，则实数k的取值范围是 ﹣2＜k＜．‎ ‎ ．‎ ‎13、（2013百色）如图，在平面直角坐标系中，直线l：y＝x＋1交x轴于点A，交y轴于点B，点A1、A2、A3，…在x轴上，点B1、B2、B3，…在直线l上。若△OB1A1，△A1B2A2，△A2B3A3，…均为等边三角形，则△A5B6A6的周长是（ ）‎ A．24 B．48 C．96 D．192‎ ‎【答案】C。‎ ‎14、（2013河池）已知二次函数y＝－x2＋3 x － ,当自变量x取m对应的函数值大于0，设自变量分别取m－3，m＋3 时对应的函数值为y1,y2，则( ）‎ A．y1＞0,y2＞0 B．y1＞0,y2＜0 C．y1＜0,y2＞0 D．y1＜0,y2＜0‎ ‎15、（2013宁波）如图，等腰直角三角形ABC顶点A，C在x轴上，∠BCA=90°，AC=BC=，反比例函数的图象分别与AB，BC交于点D,E.当∽时，点E的坐标为 ‎ 故答案是：（，）．‎ ‎15、（2013乌鲁木齐）如图所示的数码叫“莱布尼茨调和三角形”，它们是由整数的倒数组成的，第n行有n个数，且两端的数均为，每个数是它下一行左右相邻两数的和，则第8行第3个数（从左往右数）为（　B　）‎ ‎　‎ A．‎ B．‎ C．‎ D．‎ ‎16、（2013贺州）已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，给出以下结论：①b2＞4ac；②abc＞0；③2a﹣b=0；④8a+c＜0；⑤9a+3b+c＜0，其中结论正确的是　①②⑤　．（填正确结论的序号）‎ ‎17、（2013柳州）有下列4个命题： ‎ ‎①方程x2﹣（+）x+=0的根是和．‎ ‎②在△ABC中，∠ACB=90°，CD⊥AB于D．若AD=4，BD=，则CD=3．‎ ‎③点P（x，y）的坐标x，y满足x2+y2+2x﹣2y+2=0，若点P也在y=的图象上，则k=﹣1．‎ ‎④若实数b、c满足1+b+c＞0，1﹣b+c＜0，则关于x的方程x2+bx+c=0一定有两个不相等的实数根，且较大的实数根x0满足﹣1＜x0＜1．‎ 上述4个命题中，真命题的序号是　①②③④　．‎ ‎18、（2013南宁）如图，直线y=与双曲线y=（k＞0，x＞0）交于点A，将直线y=向上平移4个单位长度后，与y轴交于点C，与双曲线y=（k＞0，x＞0）交于点B，若OA=3BC，则k的值为（　D　）‎ ‎　‎ A．‎ ‎3‎ B．‎ ‎6‎ C．‎ D．‎ ‎19、（2013玉林）一列数a1，a2，a3，…，其中a1=，an=（n为不小于2的整数），则a100=（A　　）‎ ‎　‎ A．‎ B．‎ ‎2‎ C．‎ ‎﹣1‎ D．‎ ‎﹣2‎ ‎20、（2013海南）直线l1∥l2∥l3，且l1与l2的距离为1，l2与l3的距离为3，把一块含有45°角的直角三角形如图放置，顶点A，B，C恰好分别落在三条直线上，AC与直线l2交于点D，则线段BD的长度为（A　　）‎ A. B. C. D. ‎ ‎21、（2013齐齐哈尔）已知二次函数y=ax2+bx+c（a≠0）的图象经过点（x1，0）、（2，0），且﹣2＜x1＜﹣1，与y轴正半轴的交点在（0，2）的下方，则下列结论：①abc＜0；②b2＞4ac；③2a+b+1＜0；④2a+c＞0．则其中正确结论的序号是（　C　）‎ ‎　‎ A．‎ ‎①②‎ B．‎ ‎②③‎ C．‎ ‎①②④‎ D．‎ ‎①②③④‎ ‎22、（2013齐齐哈尔）正方形ABCD中，AC、BD相交于点O，点E是射线AB上一点，点F是直线AD上一点，BE=DF，连接EF交线段BD于点G，交AO于点H．若AB=3，AG=，则线段EH的长为　或　．‎ ‎23、）（2013绥化）已知：如图在△ABC，△ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE，点C，D，E三点在同一条直线上，连接BD，BE．以下四个结论：‎ ‎①BD=CE；②BD⊥CE；③∠ACE+∠DBC=45°；④BE2=2（AD2+AB2），‎ 其中结论正确的个数是（　C　）‎ ‎　‎ A．‎ ‎1‎ B．‎ ‎2‎ C．‎ ‎3‎ D．‎ ‎4‎ ‎24、（2013绥化）如图，在Rt△ABC中，∠C=90°，AC=，BC=1，D在AC上，将△ADB沿直线BD翻折后，点A落在点E处，如果AD⊥ED，那么△ABE的面积是（A　　）‎ ‎　‎ A．‎ ‎1‎ B．‎ C．‎ D．‎ ‎25、（2013随州）如图，正方形ABCD中，AB=3，点E在边CD上，且CD=3DE．将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连接AG，CF．下列结论：①点G是BC中点；②FG=FC；③S△FGC=．‎ 其中正确的是（B　　）‎ ‎　‎ A．‎ ‎①②‎ B．‎ ‎①③‎ C．‎ ‎②③‎ D．‎ ‎①②③‎ ‎26、（2013随州）如图是一组密码的一部分．为了保密，许多情况下可采用不同的密码，请你运用所学知识找到破译的“钥匙”．目前，已破译出“今年考试”的真实意思是“努力发挥”．若“今”所处的位置为（x，y），你找到的密码钥匙是　对应文字横坐标加1，纵坐标加2　，破译“正做数学”的真实意思是　祝你成功　．‎ ‎ ‎ ‎27、（2013永州）我们知道，一元二次方程x2=﹣1没有实数根，即不存在一个实数的平方等于﹣1．若我们规定一个新数“i”，使其满足i2=﹣1（即方程x2=﹣1有一个根为i）．并且进一步规定：一切实数可以与新数进行四则运算，且原有运算律和运算法则仍然成立，于是有i1=i，i2=﹣1，i3=i2•i=（﹣1）•i=﹣i，i4=（i2）2=（﹣1）2=1，从而对于任意正整数n，我们可以得到i4n+1=i4n•i=（i4）n•i=i，同理可得i4n+2=﹣1，i4n+3=﹣i，i4n=1．那么i+i2+i3+i4+…+i2012+i2013的值为（D　　）‎ ‎　‎ A．‎ ‎0‎ B．‎ ‎1‎ C．‎ ‎﹣1‎ D．‎ i ‎28、（2013•常州）二次函数y=ax2+bx+c（a、b、c为常数且a≠0）中的x与y的部分对应值如下表：‎ x ‎﹣3‎ ‎﹣2‎ ‎﹣1‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ y ‎12‎ ‎5‎ ‎0‎ ‎﹣3‎ ‎﹣4‎ ‎﹣3‎ ‎0‎ ‎5‎ ‎12‎ 给出了结论：‎ ‎（1）二次函数y=ax2+bx+c有最小值，最小值为﹣3；‎ ‎（2）当时，y＜0；‎ ‎（3）二次函数y=ax2+bx+c的图象与x轴有两个交点，且它们分别在y轴两侧．‎ 则其中正确结论的个数是（　B　）‎ ‎　‎ A．‎ ‎3‎ B．‎ ‎2‎ C．‎ ‎1‎ D．‎ ‎0‎ ‎29、（2013苏州）如图，在平面直角坐标系中，Rt△OAB的顶点A在x轴的正半轴上．顶点B的坐标为（3，），点C的坐标为（，0），点P为斜边OB上的一个动点，则PA+PC的最小值为（ B　　）‎ ‎　‎ A．‎ B．‎ C．‎ D．‎ ‎2‎ ‎30、（2013苏州）如图，在矩形ABCD中，点E是边CD的中点，将△ADE沿AE折叠后得到△AFE，且点F在矩形ABCD内部．将AF延长交边BC于点G．若=，则=　　用含k的代数式表示）．‎ ‎31、（2013扬州）如图，已知⊙O的直径AB=6，E、F为AB的三等分点，M、N为上两点，且∠MEB=∠NFB=60°，则EM+FN=　　．‎ ‎32、（2013本溪）如图，点B1是面积为1的等边△OBA的两条中线的交点，以OB1为一边，构造等边△OB1A1（点O，B1，A1按逆时针方向排列），称为第一次构造；点B2是△OBA的两条中线的交点，再以OB2为一边，构造等边△OB2A2（点O，B2，A2按逆时针方向排列），称为第二次构造；以此类推，当第n次构造出的等边△OBnAn的边OAn与等边△OBA的边OB第一次重合时，构造停止．则构造出的最后一个三角形的面积是　　．‎ ‎33、（2013铁岭）如图，点G、E、A、B在一条直线上，Rt△EFG从如图所示是位置出发，沿直线AB向右匀速运动，当点G与B重合时停止运动．设△EFG与矩形ABCD重合部分的面积为S，运动时间为t，则S与t的图象大致是（D　　）‎ ‎　‎ A．‎ B．‎ C．‎ D．‎ ‎34、（2013铁岭）如图，在平面直角坐标中，直线l经过原点，且与y轴正半轴所夹的锐角为60°，过点A（0，1）作y轴的垂线交于点B，过点B作直线的垂线交y轴于点A1，以A1B．BA为邻边作□ABA1C1；过点A1作y轴的垂线交直线于点B1，过点B1作直线l的垂线交y轴于点A2，以A2B1．B1A1为邻边作□A1B1A2C2；…；按此作法继续下去，则Cn的坐标是　（﹣×4n﹣1，4n）　．‎ ‎35、（2013淄博）如下表，从左到右在每个小格中都填入一个整数，使得任意三个相邻格子所填整数之和都相等，则第2013个格子中的整数是　﹣2　．‎ ‎﹣4‎ a b c ‎6‎ b ‎﹣2‎ ‎…‎ ‎36、（2013德阳）如图，在⊙O上有定点C和动点P，位于直径AB的异侧，过点C作CP的垂线，与PB的延长线交于点Q，已知：⊙O半径为，tan∠ABC=，则CQ的最大值是（　D　）‎ ‎　‎ A．‎ ‎5‎ B．‎ C．‎ D．‎ ‎37、（2013泸州）如图，点P1（x1，y1），点P2（x2，y2），…，点Pn（xn，yn）在函数（x＞0）的图象上，△P1OA1，△P2A1A2，△P3A2A3，…，△PnAn﹣1An都是等腰直角三角形，斜边OA1、A1A2、A2A3，…，An﹣1An都在x轴上（n是大于或等于2的正整数），则点P3‎ 的坐标是　（+，﹣）　；点Pn的坐标是　（+，﹣）　（用含n的式子表示）．‎ ‎38、（2013眉山）如图，在函数y1=（x＜0）和y2=（x＞0）的图象上，分别有A、B两点，若AB∥x轴，交y轴于点C，且OA⊥OB，S△AOC=，S△BOC=，则线段AB的长度=　　．‎ ‎39、（2013绵阳）二次函数y=ax2+bx+c的图象如图所示，给出下列结论：‎ ‎①2a+b＞0；②b＞a＞c；③若﹣1＜m＜n＜1，则m+n＜﹣；④3|a|+|c|＜2|b|．‎ 其中正确的结论是　①③④　（写出你认为正确的所有结论序号）．‎ ‎40、（2013重庆）下列图形都是由同样大小的棋子按一定的规律组成，其中第①个图形有1棵棋子，第②个图形一共有6棵棋子，第③个图形一共有16棵棋子，…，则第⑥个图形中棋子的颗数为（　C　）‎ ‎　‎ A．‎ ‎51‎ B．‎ ‎70‎ C．‎ ‎76‎ D．‎ ‎81‎ ‎41、（2013重庆）如图，在直角坐标系中，正方形OABC的顶点O与原点重合，顶点A、C分别在x轴、y轴上，反比例函数（k≠0，x＞0）的图象与正方形的两边AB、BC分别交于点M、N，ND⊥x轴，垂足为D，连接OM、ON、MN．下列结论：‎ ‎①△OCN≌△OAM；②ON=MN；③四边形DAMN与△MON面积相等；④若∠MON=45°，MN=2，则点C的坐标为（0，）．‎ 其中正确结论的个数是（C　　）‎ ‎　‎ A．‎ ‎1‎ B．‎ ‎2‎ C．‎ ‎3‎ D．‎ ‎4‎ ‎42、（2013湖北咸宁，16，3分对于二次函数，有下列说法：‎ ‎①它的图象与轴有两个公共点；‎ ‎②如果当≤1时随的增大而减小，则；‎ ‎③如果将它的图象向左平移3个单位后过原点，则；‎ ‎④如果当时的函数值与时的函数值相等，则当时的函数值为．‎ 其中正确的说法是 ．（把你认为正确说法的序号都填上）【答案】①④（‎ ‎43、如图，在边长为10的菱形ABCD中，对角线BD=16.点E是AB的中点，P、Q是BD上的动点，且始终保持PQ=2.则四边形AEPQ周长的最小值为_________．（结果保留根号）‎ 答案：7+根号85‎ 如图所示：‎ 将菱形ABCD放置在平面直角坐标系中，使得B为原点，BD在x的正半轴上，‎ ‎∵菱形ABCD的边长是10，对角线BD=16，点E是AB的中点，‎ ‎∴A（8，6），B（0，0），E（4，3），将A平行向左移动2个单位到A'点，则A'（6，6），作A'关于x轴的对称点F，则F（6，-6），连EF，交x轴于点P，在x轴上向正方向上截取PQ=2，此时，四边形AEPQ的周长最小，‎ ‎44、如图，在△ABC中，∠ACB=52°，点D，E分别是AB、AC的中点．若点F在线段DE上，且∠AFC=90°， 则∠FAE的度数为 °．答案：64‎ ‎45、如图，在Rt△ABC中，∠ABC=90°，AB=3，BC=4，P是BC边上的动点，设BP=x，若能在AC边上找到一点Q，使∠BQP=90°，则x的取值范围是____．‎ ‎46、（2011湖北黄石）初三年级某班有54名学生，所在教室有6行 9列座位，用（m，n）表示第m行第n列的座位，新学期准备调整座位，设某个学生原来的座位为（m，n），如果调整后的座位为（i，j）,则称该生作了平移[a,b]=[m-i，n-j]，并称a+b为该生的位置数。若某生的位置数为10，则当m+n取最小值时，m·n的最大值为 。 ‎ ‎【答案】36‎ 解：由已知，得a、b、m、n、i、j均为正整数 且a+b=m-i+n-j，即m-i+n-j=10，‎ ‎∴m+n=10+i+j，‎ 当i+j取得最小值为2时，m+n取得最小值 ‎∴m+n的最小值为12，‎ ‎∵m+n=12=1+11=2+10=3+9=4+8=…=6+6=…，‎ m•n的最大值为6×6=36．‎ 故答案为：36．‎ ‎47、（2011河北）如图9，给正五边形的顶点依次编号为1，2，3，4， 5.若从某一顶点开始，沿正五边形的边顺时针方向行走，顶点编号的数字是几，就走几个边长，则称这种走法为一次“移位”.  如：小宇在编号为3的顶点上时，那么他应走3个边长，即从3→4→5→1为第一次“移位”，这时他到达编号为1的顶点；然后从1→2 为第二次“移位”. 若小宇从编号为2的顶点开始，第10次“移位”后，则他所处顶点的编号为_ _．  ‎ ‎【答案】3‎ 解：． 2①→3→4②→5→1→2→3③→4→5→1④→2，∴四次移位为一个循环返回顶点2，第10次“移位”，即连续循环两次，再移位两次，即第十次移位所处的顶点和第二次移位所处的顶点相同 故答案为：3．‎ ‎48、（2013黄石市）在计数制中，通常我们使用的是“十进位制”，即“逢十进一”。而计数制方法很多，如60进位制：60秒化为1分，60分化为1小时；24进位制：24小时化为1天；7进位制：7天化为1周等…而二进位制是计算机处理数据的依据。已知二进位制与十进位制的比较如下表：‎ 十进位制 ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎…‎ 二进制 ‎0‎ ‎1‎ ‎10‎ ‎11‎ ‎100‎ ‎101‎ ‎110‎ ‎…‎ 请将二进制数10101010（二）写成十进制数为 .‎ 答案：‎ 解析：10101010（二）＝1×27＋1×25＋1×23＋1×2＝170‎ ‎49、（2012黄石市）“数学王子”高斯从小就善于观察和思考.在他读小学时候就能在课堂上快速的计算出，今天我们可以将高斯的做法归纳如下：‎ 令 ① ‎ ‎ ② ‎ ‎①＋②：有 解得：‎ 请类比以上做法，回答下列问题：‎ 若为正整数，，则.‎ 解：设S=3+5+7+…+（2n+1）=168①，‎ 则S=（2n+1）+…+7+5+3=168②，‎ ‎①+②得，2S=n（2n+1+3）=2×168，‎ 整理得，n2+2n-168=0，‎ 解得n1=12，n2=-14（舍去）．‎ 故答案为：12．‎ ‎50、（2014本溪）如图，边长为２的正方形的顶点在ｙ轴上，顶点在反比例函数（＞０）的图像上，已知点的坐标是（，），则的值为（ ）C A．4　　Ｂ．6　　Ｃ．8　　Ｄ．10‎ ‎51、（2014北京）在平面直角坐标系中，对于点，我们把点叫做点的伴随点，已知点的伴随点为，点的伴随点为，点的伴随点为，…，这样依次得到点，，，…，，….若点的坐标为（3，1），则点的坐标为 ，点的坐标为 ；若点的坐标为（，），对于任意的正整数，点均在轴上方，则，应满足的条件为 .‎ 答案：‎ ‎52、（2014福州）如图，已知直线分别与x轴，y轴交于A，B两点，与双曲线交于E，F两点. 若AB=2EF，则k的值是【 】129mD ‎ A． B．1 C． D．‎ ‎53、（2014抚顺）如图，将足够大的等腰直角三角板的锐角顶点放在另一个 等腰直角三角板的直角顶点处，三角板绕点在平面内转动，‎ 且的两边始终与斜边相交，交于点，交 于点，设，，，则能反映与的函数关系 的图像大致是（ ） A ‎ 解：作PH⊥AB于H，如图，‎ ‎∵△PAB为等腰直角三角形，‎ ‎∴∠A=∠B=45°，AH=BH=AB=1，‎ ‎∴△PAH和△PBH都是等腰直角三角形，‎ ‎∴PA=PB=AH=，∠HPB=45°，‎ ‎∵∠CPD的两边始终与斜边AB相交，PC交AB于点M，PD交AB于点N 而∠CPD=45°，‎ ‎∴1≤AN≤2，即1≤x≤2，‎ ‎∵∠2=∠1+∠B=∠1+45°，∠BPM=∠1+∠CPD=∠1+45°，‎ ‎∴∠2=∠BPM，‎ 而∠A=∠B，‎ ‎∴△ANP∽△BPM，‎ ‎∴=，即=，‎ ‎∴y=，‎ ‎∴y与x的函数关系的图象为反比例函数图象，且自变量为1≤x≤2．故选A．‎ ‎54、（2014抚顺）如图，已知是的中线，过点作∥交于点，连接交于点；过点作∥交于点，连接交于点；过点作∥交于点，…，如此继续，可以依次得到点，，…，和点，，…，．则 ．（用含的代数式表示）‎ ‎55、（2014•天水）如图，一段抛物线y=﹣x（x﹣1）（0≤x≤1）记为m1，它与x轴交点为O、A1，顶点为P1；将m1绕点A1旋转180°得m2，交x轴于点A2，顶点为P2；将m2绕点A2旋转180°得m3，交x轴于点A3，顶点为P3，…，如此进行下去，直至得m10，顶点为P10，则P10的坐标为（　（10.5，﹣0.25）　）．‎ ‎56、（2014•梅州）如图，弹性小球从点P（0，3）出发，沿所示方向运动，每当小球碰到矩形OABC的边时反弹，反弹时反射角等于入射角，当小球第1次碰到矩形的边时的点为P1，第2次碰到矩形的边时的点为P2，…，第n次碰到矩形的边时的点为Pn，则点P3的坐标是　（8，3）　；点P2014的坐标是　（5，0）　．‎ ‎57、(2014年广东深圳)二次函数y=ax2+bx+c图象如图，下列正确的个数为（　　）‎ ‎①bc＞0；‎ ‎②2a﹣3c＜0；‎ ‎③2a+b＞0；‎ ‎④ax2+bx+c=0有两个解x1，x2，x1＞0，x2＜0；‎ ‎⑤a+b+c＞0；‎ ‎⑥当x＞1时，y随x增大而减小．‎ ‎　 A． 2 B． 3 C． 4 D． 5‎ 解：①∵抛物线开口向上，‎ ‎∴a＞0，‎ ‎∵对称轴在y轴右侧，‎ ‎∴a，b异号即b＜0，‎ ‎∵抛物线与y轴的交点在负半轴，‎ ‎∴c＜0，‎ ‎∴bc＞0，故①正确；‎ ‎②∵a＞0，c＜0，‎ ‎∴2a﹣3c＞0，故②错误；‎ ‎③∵对称轴x=﹣＜1，a＞0，‎ ‎∴﹣b＜2a，‎ ‎∴2a+b＞0，故③正确；‎ ‎④由图形可知二次函数y=ax2+bx+c与x轴的两个交点分别在原点的左右两侧，‎ 即方程ax2+bx+c=0有两个解x1，x2，当x1＞x2时，x1＞0，x2＜0，故④正确；‎ ‎⑤由图形可知x=1时，y=a+b+c＜0，故⑤错误；‎ ‎⑥∵a＞0，对称轴x=1，‎ ‎∴当x＞1时，y随x增大而增大，故⑥错误．‎ 综上所述，正确的结论是①③④，共3个．故选B．‎ ‎58、(2014年广东深圳)如图，已知四边形ABCD为等腰梯形，AD∥BC，AB=CD，AD=，E为CD中点，连接AE，且AE=2，∠DAE=30°，作AE⊥AF交BC于F，则BF=（　　）‎ ‎　 A． 1 B． 3﹣ C． ﹣1 D． 4﹣2‎ 答案D．‎ ‎59、(2014年贵州安顺)如图，∠AOB=45°，过OA上到点O的距离分别为1，3，5，7，9，11，…的点作OA的垂线与OB相交，得到并标出一组黑色梯形，它们的面积分别 为S1，S2，S3，S4，…．观察图中的规律，第n（n为正整数）个黑色梯形的面积是Sn=　8n﹣4　．‎ ‎60、(2014年贵州安顺)如图，二次函数y=ax2+bx+c（a＞0）图象的顶点为D，其图象与x轴的交点A、B的横坐标分别为﹣1，3．与y轴负半轴交于点C，在下面五个结论中：‎ ‎①2a﹣b=0；②a+b+c＞0；③c=﹣3a；④只有当a=时，△ABD是等腰直角三角形；⑤使△ACB为等腰三角形的a值可以有四个．‎ 其中正确的结论是　③④　．（只填序号）‎ ‎61、(2014年黑龙江哈尔滨)早晨，小刚沿着通往学校唯一的一条路（直路）上学，途中发现忘带饭盒，停下往家里打电话，妈妈接到电话后带上饭盒马上赶往学校，同时小刚返回，两人相遇后，小刚立即赶往学校，妈妈回家，15分钟妈妈到家，再经过3分钟小刚到达学校，小刚始终以100米/分的速度步行，小刚和妈妈的距离y（单位：米）与小刚打完电话后的步行时间t（单位：分）之间的函数关系如图，下列四种说法：‎ ‎①打电话时，小刚和妈妈的距离为1250米；‎ ‎②打完电话后，经过23分钟小刚到达学校；‎ ‎③小刚和妈妈相遇后，妈妈回家的速度为150米/分；‎ ‎④小刚家与学校的距离为2550米．其中正确的个数是（　　）‎ ‎　 A． 1个 B． 2个 C． 3个 D． 4个 正确的答案有①②④．故选：C．‎ ‎62、(2014年黑龙江龙东地区）如图，等腰Rt△ABC中，∠ACB=90°，AC=BC=1，且AC边在直线a上，将△ABC绕点A顺时针旋转到位置①可得到点P1，此时AP1=；将位置①的三角形绕点P1顺时针旋转到位置②，可得到点P2，此时AP2=1+；将位置②的三角形绕点P2顺时针旋转到位置③，可得到点P3，此时AP3=2+；…，按此规律继续旋转，直至得到点P2014为止．则AP2014=　1342+672　．‎ 解答： 解：AP1=，AP2=1+，AP3=2+；‎ AP4=2+2；AP5=3+2；AP6=4+2；‎ AP7=4+3；AP8=5+3；AP9=6+3；‎ ‎∵2013=3×671，‎ ‎∴AP2013=（2013﹣761）+671=1342+671，‎ ‎∴AP2014=1342+671+=1342+672．‎ 故答案为：1342+672．‎ ‎63、（2014•绥化）如图，在矩形ABCD中，AD=AB，∠BAD的平分线交BC于点E，DH⊥AE于点H，连接BH并延长交CD于点F，连接DE交BF于点O，下列结论：‎ ‎①∠AED=∠CED；②OE=OD；③BH=HF；④BC﹣CF=2HE；⑤AB=HF，‎ 其中正确的有（　　）B ‎　‎ A．‎ ‎2个 B．‎ ‎3个 C．‎ ‎4个 D．‎ ‎5个 ‎64、（2014呼和浩特）已知函数y = 的图象在第一象限的一支曲线上有一点A（a，c），点B（b，c＋1）在该函数图象的另外一支上，则关于一元二次方程ax2＋bx＋c = 0的两根x1，x2判断正确的是 A．x1 ＋ x2 >1，x1·x2 > 0 B．x1 ＋ x2 < 0，x1·x2 > 0‎ C．0 < x1 ＋ x2 < 1，x1·x2 > 0 D．x1 ＋ x2与x1·x2 的符号都不确定 试题分析：∵，且点A（a，c）在第一象限的一支曲线上，点B（b，c＋1）在第二象限的一支曲线上，‎ ‎∴，且.∴.‎ 又∵x1，x2是关于一元二次方程ax2＋bx＋c = 0的两根，‎ ‎∴‎ ‎.∴.‎ 故选C．‎ ‎65、(2014年湖北随州)某通讯公司提供了两种移动电话收费方式：方式1，收月基本费20元，再以每分钟0.1元的价格按通话时间计费；方式2，收月基本费20元，送80分钟通话时间，超过80分钟的部分，以每分钟0.15元的价格计费．‎ 下列结论：‎ ‎①如图描述的是方式1的收费方法；‎ ‎②若月通话时间少于240分钟，选择方式2省钱；‎ ‎③若月通讯费为50元，则方式1比方式2的通话时间多；‎ ‎④若方式1比方式2的通讯费多10元，则方式1比方式2的通话时间多100分钟．‎ 其中正确的是（　　）‎ ‎　‎ ‎ A． 只有①② B． 只有③④ C． 只有①②③ D． ①②③④‎ 解：根据题意得：方式一的函数解析式为y=0.1x+20，方式二的函数解析式为y=0.15x+8，‎ ‎①当x=80时，方式一的收费是28元，故①说法正确；‎ ‎②0.1x+20＞0.15x+8，解得x＜240，故②的说法正确；‎ ‎③当y=50元时，方式一0.1x+20=50，解得x=300分钟，方式二0.15x+8=50，解得x=280分钟，故③说法正确；‎ ‎④0.1x+20﹣0.15x﹣8=10，解得x=40，故④说法错误；‎ 故选：C．‎ ‎66、（2014年江苏盐城）如图，在平面直角坐标系中，边长不等的正方形依次排列，每个正方形都有一个顶点落在函数y=x的图象上，从左向右第3个正方形中的一个顶点A的坐标为（8，4），阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn，则Sn的值为　24n﹣5　．（用含n的代数式表示，n为正整数）‎ ‎67、（2014•丹东）如图，在菱形ABCD中，AB=4cm，∠ADC=120°，点E、F同时由A、C两点出发，分别沿AB、CB方向向点B匀速移动（到点B为止），点E的速度为1cm/s，点F的速度为2cm/s，经过t秒△DEF为等边三角形，则t的值为　　．‎ ‎68、（2014盘锦市）如图，在平面直角坐标系中，点A和点B分别在x轴和y轴的正半轴上，OA=OB=a，以线段AB为边在第一象限作正方形ABCD，CD的延长线交x轴于点E，再以CE为边作第二个正方形ECGF，…，依此方法作下去，则第n个正方形的边长是 . ‎ ‎69、（2014•营口）如图，在平面直角坐标系中，直线l：y=x，直线l2：y=x，在直线l1上取一点B，使OB=1，以点B为对称中心，作点O的对称点B1，过点B1作B1A1∥l2，交x轴于点A1，作B1C1∥x轴，交直线l2于点C1，得到四边形OA1B1C1；再以点B1为对称中心，作O点的对称点B2，过点B2作B2A2∥l2，交x轴于点A2，作B2C2∥x轴，交直线l2于点C2，得到四边形OA2B2C2；…；按此规律作下去，则四边形OAnBnCn的面积是　　．‎ ‎70、（2014•泸州）如图，矩形AOBC的顶点坐标分别为A（0，3），O（0，0），B（4，0），C（4，3），动点F在边BC上（不与B、C重合），过点F的反比例函数的图象与边AC交于点E，直线EF分别与y轴和x轴相交于点D和G．给出下列命题：‎ ‎①若k=4，则△OEF的面积为；‎ ‎②若，则点C关于直线EF的对称点在x轴上；‎ ‎③满足题设的k的取值范围是0＜k≤12；‎ ‎④若DE•EG=，则k=1．‎ 其中正确的命题的序号是　②④　（写出所有正确命题的序号）．‎ ‎71、（2014•聊城）如图，在x轴的正半轴上依次间隔相等的距离取点A1，A2，A3，A4，…，An分别过这些点做x轴的垂线与反比例函数y=的图象相交于点P1，P2，P3，P4，…Pn作P2B1⊥A1P1，P3B2⊥A2P2，P4B3⊥A3P3，…，PnBn﹣1⊥An﹣1Pn﹣1，垂足分别为B1，B2，B3，B4，…，Bn﹣1，连接P1P2，P2P3，P3P4，…，Pn﹣1Pn，得到一组Rt△P1B1P2，Rt△P2B2P3，Rt△P3B3P4，…，Rt△Pn﹣1Bn﹣1Pn，则Rt△Pn﹣1Bn﹣1Pn的面积为　．　．‎ ‎72、（2014•日照）如图，已知△ABC的面积是12，点E、I分别在边AB、AC上，在BC边上依次作了n个全等的小正方形DEFG，GFMN，…，KHIJ，则每个小正方形的边长为（　　）‎ ‎　‎ A．‎ B．‎ C．‎ D．‎ 解：过C作CM⊥AB，垂足为M，交GH于点N．‎ ‎∴∠CMB=90°，‎ ‎∵四边形EFGH是正方形，‎ ‎∴GH∥AB，GH=GF，GF⊥AB，‎ ‎∴∠CGH=∠A，∠CNH=∠CMB=90°．‎ ‎∵∠GCH=∠ACB，‎ ‎∴△CGH∽△CAB．‎ ‎∴，‎ ‎∵GF=MN=GH，设GH=x，三角形ABC的底为a，高为h，‎ ‎∴CN=CM﹣MN=CM﹣GH=CM﹣x．‎ ‎∴，‎ ‎…以此类推，‎ 由此，当为n个正方形时以x=，‎ 故选D．‎ ‎73、（2014年山东烟台）二次函数y=ax2+bx+c（a≠0）的部分图象如图，图象过点（﹣1，0），对称轴为直线x=2，下列结论：‎ ‎①4a+b=0；②9a+c＞3b；③8a+7b+2c＞0；④当x＞﹣1时，y的值随x值的增大而增大．‎ 其中正确的结论有（　　）B ‎　 A．1个 B． 2个 C． 3个 D． 4个 ‎74、已知,是同一个反比例函数图像上的两点.若,且 ‎，则这个反比例函数的表达式为_________. ‎ ‎75、（2014年四川巴中）已知二次函数y=ax2+bx+c的图象如图，则下列叙述正确的是（　　）‎ ‎　 ‎ A． abc＜0　　　B． ﹣3a+c＜0 C． b2﹣4ac≥0‎ D． 将该函数图象向左平移2个单位后所得到抛物线的解析式为y=ax2+c ‎76、（2014•德阳）在四边形ABCD中，AD∥BC，∠ABC=90°，AB=BC，E为AB边上一点，∠BCE=15°，且AE=AD．连接DE交对角线AC于H，连接BH．下列结论正确的是　①③④　．（填番号）‎ ‎①AC⊥DE；②=；③CD=2DH；④=．‎ ‎77、(2014年四川资阳)二次函数y=ax2+bx+c（a≠0）的图象如图，给出下列四个结论：‎ ‎①4ac﹣b2＜0；②4a+c＜2b；③3b+2c＜0；④m（am+b）+b＜a（m≠﹣1），‎ 其中正确结论的个数是（　　）B ‎　 A． 4个 B． 3个 C． 2个 D． 1个 ‎78、(2014年四川资阳)如图，以O（0，0）、A（2，0）为顶点作正△OAP1，以点P1和线段P1A的中点B为顶点作正△P1BP2，再以点P2和线段P2B的中点C为顶点作△P2CP3，…，如此继续下去，则第六个正三角形中，不在第五个正三角形上的顶点P6的坐标是　（，）　．‎ ‎79、（2014台湾）数轴上A、B、C三点所代表的数分别是a、1、c，且 | c-1 |-| a-1 |=| a-c |。若下列选项中，有一个表示A、B、C三点在数轴上的位置关系，则此选项为（ ）A ‎(A)‎ A B C ‎(B)‎ B C A ‎(C)‎ C A B ‎(D C B A ‎80、(2014•台湾)如图数轴上有A、B、C、D四点，根据图中各点的位置，判断那一点所表示的数与11﹣2最接近？(　　)B A．A B．B C．C D．D ‎81、（2015桂花九义校模拟）已知二次函数过点（0，）和（，2m）对于该二次函数有如下说法：①它的图象与轴有两个公共点；‎ ‎②若存在一个正数x0，使得当x0；若存在一个负数x0，使得当x>x0时，函数值y随x的增大而增大，则<0；‎ ‎③若将它的图象向左平移3个单位后过原点，则；‎ ‎④若当时的函数值与时的函数值相等，则当时的函数值为．‎ 其中正确的说法的个数是（ C ）‎ A. 1 B. 2 C. 3 D. 4‎ ‎82、如图放置的△OAB1，△B1A1B2，△B2A2B3，…都是边长为2的等边三角形，边AO在y轴上，点B1，B2，B3，…都在直线y=x上，则A2015的坐标是　 （2015，2017） 　．‎ ‎83、二次函数y=ax2+bx+c的图象如图所示，给出下列结论：‎ ‎①2a+b＞0；②b＞a＞c；③若﹣1＜m＜n＜1，则m+n＜﹣；④3|a|+|c|＜2|b|．其中正确的结论是（ D ）‎ A．①②③ B．①③ C．①③④ D．①④ ‎ ‎84、有下列4个命题：‎ ‎①方程x2﹣（+）x+=0的根是和．‎ ‎②在△ABC中，∠ACB=90°，CD⊥AB于D．若AD=4，BD=，则CD=3．‎ ‎③点P（x，y）的坐标x，y满足x2+y2+2x﹣2y+2=0，若点P也在y=的图象上，则k=﹣1．‎ ‎④若实数b、c满足1+b+c＞0，1﹣b+c＜0，则关于x的方程x2+bx+c=0一定有两个不相等的实数根，且较大的实数根x0满足﹣1＜x0＜1．‎ 上述4个命题中，真命题的序号是　　 ①②③④ ．‎ ‎85、已知函数y = 的图象在第一象限的一支曲线上有一点A（a，c），点B（b，c＋1）在该函数图象的另外一支上，则关于一元二次方程ax2＋bx＋c = 0的两根x1，x2判断正确的是（ ）‎ A．x1 ＋ x2 >1，x1·x2 > 0 B．x1 ＋ x2 < 0，x1·x2 > 0‎ C．0 < x1 ＋ x2 < 1，x1·x2 > 0 D．x1 ＋ x2与x1·x2 的符号都不确定 ‎86、（2015桂花九义校模拟）如图，给正五边形的顶点依次编号为1，2，3，4， 5.若从某一顶点开始，沿正五边形的边顺时针方向行走，顶点编号的数字是几，就走几个边长，则称这种走法为一次“移位”.  如：小宇在编号为3的顶点上时，那么他应走3个边长，即从3→4→5→1为第一次“移位”，这时他到达编号为1的顶点；然后从1→2 为第二次“移位”. 若小宇从编号为2的顶点开始，第10次“移位”后，则他所处顶点的编号为_ _．  ‎ ‎87、二次函数的图象如图，对称轴为．若关于的一元二次方程（为实数）在的范围内有解，则的取值范围是（ C ）‎ A． 　　 B． ‎ C． 　　　 D．‎ ‎1‎ Ｂ Ｏ x y ‎4‎ ‎88、如图，点B1是面积为1的等边△OBA的两条中线的交点，以OB1为一边，构造等边△OB1A1（点O，B1，A1按逆时针方向排列），称为第一次构造；点B2是△OBA的两条中线的交点，再以OB2为一边，构造等边△OB2A2（点O，B2，A2按逆时针方向排列），称为第二次构造；以此类推，当第n次构造出的等边△OBnAn的边OAn与等边△OBA的边OB第一次重合时，构造停止．则构造出的最后一个三角形的面积是　 　．‎ ‎89、如图,已知抛物线y1=－2x2＋2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2，取y1、y2中的较小值记为M；若y1=y2，记M= y1=y2.例如：当x=1时 x y O y2‎ y1‎ ，y1=0,y2=4,y1＜y2，此时M=0. 下列判断： ‎ ‎①当x＞0时，y1＞y2； ②当x＜0时，x值越大，M值越小；‎ ‎③使得M大于2的x值不存在； ④使得M=1的x值是 或.‎ 其中正确的是 ( D )‎ A. ①② B.①④ C.②③ D.③④‎ ‎90、如图，在边长为2的菱形ABCD中，∠A=60°，M是AD边的中点，N是AB边上的一动点，将△AMN沿MN所在直线翻折得到△A′MN，连接A′C，则A′C长度的最小值是　﹣1　．‎ ‎91、当时，二次函数有最大值4，则实数的值为（ C ）‎ ‎(A) (B) 或 (C) 或 (D) 或或 ‎92、如图，在平面直角坐标系中，边长不等的正方形依次排列，每个正方形都有一个顶点落在函数y=x的图象上，从左向右第3个正方形中的一个顶点A的坐标为（8，4），阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn，则Sn的值为　24n﹣5 　．（用含n的代数式表示，n为正整数）‎ ‎93、（2015桂花九义校模拟）二次函数y=ax2+bx+c（a≠0）图象如图，下列结论：‎ ‎①abc＞0；②3a+c<0；③当m≠1时，a+b＞am2+bm；‎ ‎④a﹣b+c＞0；⑤若ax12+bx1=ax22+bx2，且x1≠x2，则x1+x2=2．‎ 其中正确的是（　D　）‎ ‎ A．①②③ B．②④ C．②⑤ D．②③⑤‎ ‎94、如图，菱形ABCD中，∠A=60°，AB=3，⊙A、⊙B的半径分别为2和1，P、E、F分别是边CD、⊙A和⊙B上的动点，则PE+PF的最小值是　 3 　．‎ ‎95、（2015桂花九义校模拟）将自然数按以下规律排列：‎ 第一列　第二列　第三列　第四列　第五列 第一行　　　1 4 5 16 17 …‎ 第二行　　　2 3 6 15 …‎ 第三行　　　9 8 7 14 …‎ 第四行　　　10 11 12 13 …‎ 第五行 …‎ ‎……‎ 表中数2在第二行，第一列，与有序数对（2,1）对应；数5与（1,3）对应；数14与（3,4）对应；根据这一规律，数2015对应的有序数对为 （45,11） ．‎ ‎96、如图，E，F是正方形ABCD的边AD上两个动点，满足AE＝DF．连结CF交BD于G，连结BE交AG于点H．若正方形的边长为2，则线段DH长度的最小值是 ．‎ ‎97、（2015桂花九义校模拟）设a1，a2，…， a2015是从1，0，﹣1这三个数中取值的一列数，若a1+a2+…+ a2015=69，（a1+1）2+（a2+1）2+…+（a2015+1）2=4002，则a1，a2，…，a2015中为0的个数是　166 .‎ ‎98、（2015桂花九义校模拟）如图，一条抛物线与x轴相交于A、B两点，其顶点P在折线C－D－E上移动，若点C、D、E的坐标分别为（-1，4）、（3，4）、（3，1），点B的横坐标的最小值为1， 则点A的横坐标的最大值为（ B ） ‎ A.1   B.2   C.3   D.4‎ ‎99、如图，以O（0，0）、A（2，0）为顶点作正△OAP1，以点P1和线段P1A的中点B为顶点作正△P1BP2，再以点P2和线段P2B的中点C为顶点作△P2CP3，…，如此继续下去，则第六个正三角形中，不在第五个正三角形上的顶点P6的坐标是　 （，） 　．‎ ‎100、如图，抛物线y=ax2+bx+c（a≠0）过点（1，0）和点（0，﹣2），且顶点在第三象限，设P=a﹣b+c，则P的取值范围是（　B　）‎ A．﹣4＜P＜﹣2 B． ﹣4＜P＜0‎ C．﹣2＜P＜0 D．﹣1＜P＜0‎ ‎101、（2015桂花九义校模拟）如图，A点的初始位置位于数轴上的原点，现对A点做如下移动：‎ 第1次从原点向右移动1个单位长度至B点，‎ 第2次从B点向左移动3个单位长度至C点，‎ 第3次从C点向右移动6个单位长度至D点，‎ 第4次从D点向左移动9个单位长度至E点，…，‎ 依此类推，这样至少移动 28 次后该点到原点的距离不小于41．‎ ‎102、（2014•湖州）在连接A地与B地的线段上有四个不同的点D、G、K、Q，下列四幅图中的实线分别表示某人从A地到B地的不同行进路线（箭头表示行进的方向），则路程最长的行进路线图是（　 D　）‎ ‎　 A． B． ‎ C． D．‎ ‎103、（2014•湖州）已知当x1=a，x2=b，x3=c时，二次函数y=x2+mx对应的函数值分别为y1，y2，y3，若正整数a，b，c恰好是一个三角形的三边长，且当a＜b＜c时，都有y1＜y2＜y3，则实数m的取值范围是　m＞﹣．　．‎ ‎104、（2014•扬州）如图，在四边形ABCD中，AB=AD=6，AB⊥BC，AD⊥CD，∠BAD=60°，点M、N分别在AB、AD边上，若AM：MB=AN：ND=1：2，则tan∠MCN=（　A　）‎ ‎　‎ A．‎ B．‎ C．‎ D．‎ ‎﹣2‎ ‎105、（2014•荆州）如图，已知点A是双曲线y=在第一象限的分支上的一个动点，连结AO并延长交另一分支于点B，以AB为边作等边△ABC，点C在第四象限．随着点A的运动，点C的位置也不断变化，但点C始终在双曲线y=（k＜0）上运动，则k的值是　﹣6　．‎ ‎106、（2014•德州）如图，抛物线y=x2在第一象限内经过的整数点（横坐标、纵坐标都为整数的点）依次为A1，A2，A3…An，…．将抛物线y=x2沿直线L：y=x向上平移，得一系列抛物线，且满足下列条件：‎ ‎①抛物线的顶点M1，M2，M3，…Mn，…都在直线L：y=x上；‎ ‎②抛物线依次经过点A1，A2，A3…An，…．‎ 则顶点M2014的坐标为（　4027　，　4027　）．‎