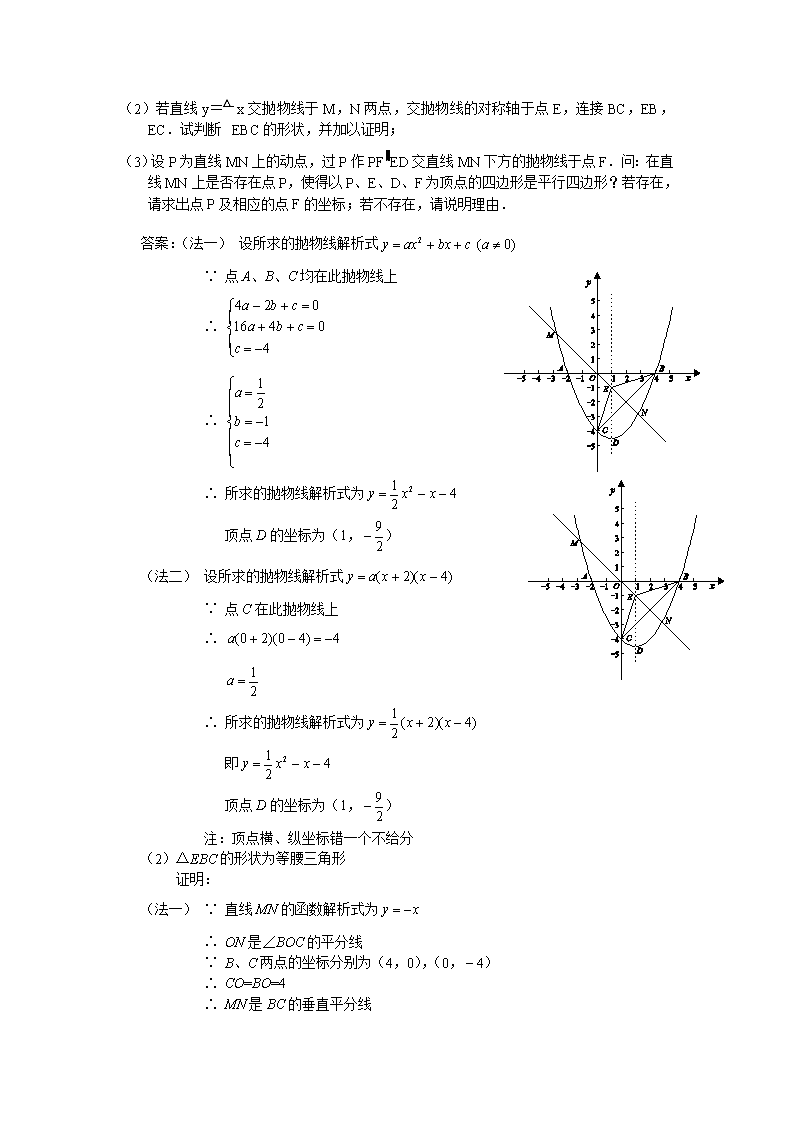- 7.03 MB
- 2021-05-13 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
25.(2010湖南湘潭市)(本题满分10分)
如图,在直角梯形ABCD中,AB∥DC,∠D=90o,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0MN成立的x的取值范围。
解:(1)∠ABE=∠CBD=30°
在△ABE中,AB=6
BC=BE=
CD=BCtan30°=4
∴OD=OC-CD=2
∴B(,6) D(0,2)
设BD所在直线的函数解析式是y=kx+b
∴
所以BD所在直线的函数解析式是
(2)∵EF=EA=ABtan30°= ∠FEG=180°-∠FEB-∠AEB=60°
(2010红河自治州)22.(本小题满分11分)二次函数的图像如图8所示,请将此图像向右平移1个单位,再向下平移2个单位.
(1)画出经过两次平移后所得到的图像,并写出函数的解析式.
(2)求经过两次平移后的图像与x轴的交点坐标,指出当x满足什么条件时,函数值大于0?
解:画图如图所示:
依题意得:
=
=
∴平移后图像的解析式为:
(2)当y=0时,=0
∴平移后的图像与x轴交与两点,坐标分别为(,0)和(,0)
由图可知,当x<或x>时,二次函数的函数值大于0.
(2010年镇江市)12.已知实数的最大值为 4 .
(2010年镇江市)23.运算求解(本小题满分6分)
已知二次函数的图象C1与x轴有且只有一个公共点.
(1)求C1的顶点坐标;
(2)将C1向下平移若干个单位后,得抛物线C2,如果C2与x轴的一个交点为A(—3,0),求C2的函数关系式,并求C2与x轴的另一个交点坐标;
(3)若的取值范围.
(1) (1分)
轴有且只有一个公共点,∴顶点的纵坐标为0.
∴C1的顶点坐标为(—1,0) (2分)
(2)设C2的函数关系式为
把A(—3,0)代入上式得
∴C2的函数关系式为 (3分)
∵抛物线的对称轴为轴的一个交点为A(—3,0),由对称性可知,它与x轴的另一个交点坐标为(1,0). (4分)
(3)当的增大而增大,
当 (5分)
(9题图)
(2010遵义市)如图,两条抛物线、与分别经过点,且平行于轴的两条平行线围成的阴影部分的面积为
A.8 B.6 C.10 D.4
答案:A
(2010台州市)10.如图,点A,B的坐标分别为(1, 4)和(4, 4),抛物线的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为,则点D的横坐标最大值为(▲)
y
x
O
(第10题)
A.-3 B.1 C.5 D.8
答案:D
(2010遵义市)(14分)如图,已知抛物线的顶点坐
(27题图)
标为Q,且与轴交于点C,与轴交于A、B两
点(点A在点B的右侧),点P是该抛物线上一动点,从点C
沿抛物线向点A运动(点P与A不重合),过点P作PD∥轴,
交AC于点D.
(1)求该抛物线的函数关系式;
(2)当△ADP是直角三角形时,求点P的坐标;
(3)在问题(2)的结论下,若点E在轴上,点F在抛物线上,
问是否存在以A、P、E、F为顶点的平行四边形?若存在,
求点F的坐标;若不存在,请说明理由.
答案: 27.(14分)解:(1)(3分)
∵抛物线的顶点为Q(2,-1)
∴设
将C(0,3)代入上式,得
∴, 即
(2)(7分)分两种情况:
①(3分)当点P1为直角顶点时,点P1与点B重合(如图)
令=0, 得
解之得,
∵点A在点B的右边, ∴B(1,0), A(3,0)
∴P1(1,0)
②(4分)解:当点A为△APD2的直角顶点是(如图)
∵OA=OC, ∠AOC=, ∴∠OAD2=
当∠D2AP2=时, ∠OAP2=, ∴AO平分∠D2AP2
又∵P2D2∥轴, ∴P2D2⊥AO, ∴P2、D2关于轴对称.
设直线AC的函数关系式为
将A(3,0), C(0,3)代入上式得
, ∴
∴
∵D2在上, P2在上,
∴设D2(,), P2(,)
∴()+()=0
, ∴, (舍)
∴当=2时,
==-1
∴P2的坐标为P2(2,-1)(即为抛物线顶点)
∴P点坐标为P1(1,0), P2(2,-1)
(3)(4分)解: 由题(2)知,当点P的坐标为P1(1,0)时,不能构成平行四边形
当点P的坐标为P2(2,-1)(即顶点Q)时,
平移直线AP(如图)交轴于点E,交抛物线于点F.
当AP=FE时,四边形PAFE是平行四边形
∵P(2,-1), ∴可令F(,1)
∴
解之得: ,
∴F点有两点,即F1(,1), F2(,1)
(2010台州市)(第24题)
H
24.如图,Rt△ABC中,∠C=90°,BC=6,AC=8.点P,Q都是斜边AB上的动点,点P从B 向A运动(不与点B重合),点Q从A向B运动,BP=AQ.点D,E分别是点A,B以Q,P为对称中心的对称点, HQ⊥AB于Q,交AC于点H.当点E到达顶点A时,P,Q同时停止运动.设BP的长为x,△HDE的面积为y.
(1)求证:△DHQ∽△ABC;
(2)求y关于x的函数解析式并求y的最大值;
(3)当x为何值时,△HDE为等腰三角形?
24.(14分)(1)∵A、D关于点Q成中心对称,HQ⊥AB,
∴=90°,HD=HA,
∴,…………………………………………………………………………
3分
(图1)
(图2)
∴△DHQ∽△ABC. ……………………………………………………………………1分
(2)①如图1,当时,
ED=,QH=,
此时. …………………………………………3分
当时,最大值.
②如图2,当时,
ED=,QH=,
此时. …………………………………………2分
当时,最大值.
∴y与x之间的函数解析式为
y的最大值是.……………………………………………………………………1分
(3)①如图1,当时,
若DE=DH,∵DH=AH=, DE=,
∴=,.
显然ED=EH,HD=HE不可能; ……………………………………………………1分
②如图2,当时,
若DE=DH,=,; …………………………………………1分
若HD=HE,此时点D,E分别与点B,A重合,; ………………………1分
若ED=EH,则△EDH∽△HDA,
∴,,. ……………………………………1分
∴当x的值为时,△HDE是等腰三角形.
(其他解法相应给分)
图7
(玉溪市2010)15. 如图7是二次函数在平面直角坐标
系中的图象,根据图形判断 ① >0;② ++<0;
③ 2-<0; 2+8>4中正确的是(填写序号)② 、④ .
(玉溪市2010)23.如图10,在平面直角坐标系中,点A的坐标为(1,) ,△AOB的面积是.
(1)求点B的坐标;
(2)求过点A、O、B的抛物线的解析式;
x
y
A
0
B
(3)在(2)中抛物线的对称轴上是否存在点C,使△AOC的周长最小?若存在,求出点C的 坐标;若不存在,请说明理由;
(4)在(2)中,轴下方的抛物线上是否存在一点P,
过点P作轴的垂线,交直线AB于点D,线段OD
把△AOB分成两个三角形.使其中一个三角形面积
与图10
四边形BPOD面积比为2:3 ?若存在,求出
点P的坐标;若不存在,请说明理由.
解:(1)由题意得:
∴B(-2,0) …………3分
(2)设抛物线的解析式为y=ax(x+2),代入点A(1, ),得,
∴ …………6分
C
A
B
O
y
x
(3)存在点C.过点A作AF垂直于x轴于点F,抛物线
的对称轴x= - 1交x轴于点E.当点C位于对称轴
与线段AB的交点时,△AOC的周长最小.
∵ △BCE∽△BAF,
…………9分
(4)存在. 如图,设p(x,y),直线AB为y=kx+b,则
,
∴直线AB为,
= |OB||YP|+|OB||YD|=|YP|+|YD|
=.
∵S△AOD= S△AOB-S△BOD =-×2×∣x+∣=-x+.
y
x
A
O
D
B
P
∴==.
∴x1=- , x2=1(舍去).
∴p(-,-) .
又∵S△BOD =x+,
∴ == .
∴x1=- , x2=-2.
P(-2,0),不符合题意.
∴ 存在,点P坐标是(-,-). …………12分
(桂林2010)11.将抛物线绕它的顶点旋转180°,所得抛物线的解析式是( D ).
A. B.
C. D.
(桂林2010)12.如图,已知正方形ABCD的边长为4 ,E是BC边上的一个
动点,AE⊥EF, EF交DC于F, 设BE=,FC=,则当
点E从点B运动到点C时,关于的函数图象是( A ).
A. B. C. D.
(桂林2010)15.函数的自变量的取值范围是 .>1
(2010年兰州)5. 二次函数的图像的顶点坐标是
A.(-1,8) B.(1,8) C.(-1,2) D.(1,-4)
答案 A
(2010年兰州)13. 抛物线图像向右平移2个单位再向下平移3个单位,所得图像的解析式为,则b、c的值为
A . b=2, c=2 B. b=2,c=0
C . b= -2,c=-1 D. b= -3, c=2
答案 B
(2010年兰州)15. 抛物线图像如图所示,则一次函数与反比例函数 在同一坐标系内的图像大致为
x
x
x
x
x
第15题图
答案D
(2010年兰州)20. 如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给小明做了一个简易的秋千.拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为 米.
答案
(2010年兰州)28.(本题满分11分)如图1,已知矩形ABCD的顶点A与点O重合,AD、AB分别在x轴、y轴上,且AD=2,AB=3;抛物线经过坐标原点O和x轴上另一点E(4,0)
(1)当x取何值时,该抛物线的最大值是多少?
(2)将矩形ABCD以每秒1个单位长度的速度从图1所示的位置沿x轴的正方向匀速平行移动,同时一动点P也以相同的速度从点A出发向B匀速移动.设它们运动的时间为t秒(0≤t≤3),直线AB与该抛物线的交点为N(如图2所示).
① 当时,判断点P是否在直线ME上,并说明理由;
② 以P、N、C、D为顶点的多边形面积是否可能为5,若有可能,求出此时N点的坐标;若无可能,请说明理由.
图1 第28题图 图2
答案28. (本题满分11分)
解:(1)因抛物线经过坐标原点O(0,0)和点E(4,0)
故可得c=0,b=4
所以抛物线的解析式为…………………………………………1分
由
得当x=2时,该抛物线的最大值是4. …………………………………………2分
(2)① 点P不在直线ME上.
已知M点的坐标为(2,4),E点的坐标为(4,0),
设直线ME的关系式为y=kx+b.
于是得 ,解得
所以直线ME的关系式为y=-2x+8. …………………………………………3分
由已知条件易得,当时,OA=AP=,…………………4分
∵ P点的坐标不满足直线ME的关系式y=-2x+8. [来源:Zxxk.Com]
∴ 当时,点P不在直线ME上. ……………………………………5分
②以P、N、C、D为顶点的多边形面积可能为5
∵ 点A在x轴的非负半轴上,且N在抛物线上,
∴ OA=AP=t.
∴ 点P,N的坐标分别为(t,t)、(t,-t 2+4t) …………………………………6分
∴ AN=-t 2+4t (0≤t≤3) ,
∴ AN-AP=(-t 2+4 t)- t=-t 2+3 t=t(3-t)≥0 , ∴ PN=-t 2+3 t
…………………………………………………………………………………7分
(ⅰ)当PN=0,即t=0或t=3时,以点P,N,C,D为顶点的多边形是三角形,此三角形的高为AD,∴ S=DC·AD=×3×2=3.
(ⅱ)当PN≠0时,以点P,N,C,D为顶点的多边形是四边形
∵ PN∥CD,AD⊥CD,
∴ S=(CD+PN)·AD=[3+(-t 2+3 t)]×2=-t 2+3 t+3…………………8分
当-t 2+3 t+3=5时,解得t=1、2…………………………………………………9分
而1、2都在0≤t≤3范围内,故以P、N、C、D为顶点的多边形面积为5
综上所述,当t=1、2时,以点P,N,C,D为顶点的多边形面积为5,
当t=1时,此时N点的坐标(1,3)………………………………………10分
当t=2时,此时N点的坐标(2,4)………………………………………11分
说明:(ⅱ)中的关系式,当t=0和t=3时也适合.(故在阅卷时没有(ⅰ),只有(ⅱ)也可以,不扣分)
(2010年无锡)24.(本题满分10分)如图,矩形ABCD的顶点A、B的坐标分别为(-4,0)和(2,0),BC=.
设直线AC与直线x=4交于点E.
(1)求以直线x=4为对称轴,且过C与原点O的抛物线的函数关系式,并说明此抛物线一定过点E;本试卷由无锡市天一实验学校金杨建录制 QQ:623300747.转载请注明!
(2)设(1)中的抛物线与x轴的另一个交点为N,
M是该抛物线上位于C、N之间的一动点,求
△CMN面积的最大值.
答案解:(1)点C的坐标.设抛物线的函数关系式为,
则,解得
∴所求抛物线的函数关系式为…………①
设直线AC的函数关系式为则,解得.
∴直线AC的函数关系式为,∴点E的坐标为
把x=4代入①式,得,∴此抛物线过E点.
(2)(1)中抛物线与x轴的另一个交点为N(8,0),设M(x,y),过M作MG⊥x轴于G,则S△CMN=S△MNG+S梯形MGBC—S△CBN=
=
=
∴当x=5时,S△CMN有最大值
(2010年连云港)25.(本题满分10分)我市某工艺品厂生产一款工艺品.已知这款工艺品的生产成本为每件60元.经市场调研发现:该款工艺品每天的销售量y(件)与售价x(元)之间存在着如下表所示的一次函数关系.
售价x(元)
…
70
90
…
销售量y(件)
…
3000
1000
…
(利润=(售价-成本价)×销售量)
(1)求销售量y(件)与售价x(元)之间的函数关系式;
(2)你认为如何定价才能使工艺品厂每天获得的利润为40 000 元?
答案 (1)设一次函数的关系式为,根据题意得............................2分
解之得
所以所求的一次关系式为y= -100x+10000........................................................................................5分
(2)由题意得 (x-60)(-100x+10000)=40000
即所以
所以
答 当定价为80元时,才能使工艺品厂每天的利润为40000元
(2010宁波市)O
第18题
y
·P
x
18.如图,已知⊙P的半径为2,圆心P在抛物线y=x2—1上运动,当⊙P与x轴相切时,圆心P的坐标为_________________.
(2010宁波市)20.如图,已知二次函数y=— x2+bx+c的图象经过A(2,0)、B(0,—6)两点.
(1)求这个二次函数的解析式;
(2)设该二次函数图象的对称轴与x轴交于点C,连结BA、BC,求△ABC的面积.
O
第20题
y
A
x
C
B
8. (2010年金华) 已知抛物线的开口向下,顶点坐标为(2,-3) ,那么该抛物线有( ▲ )B
A. 最小值 -3 B. 最大值-3 C. 最小值2 D. 最大值2
15. (2010年金华)若二次函数的部分图象如图所示,则关于x的一元二次方程
的一个解,另一个解 ▲ ;
y
(第15题图)
O
x
1
3
答案:-1;
20.(2010年金华)(本题8分)
已知二次函数y=ax2+bx-3的图象经过点A(2,-3),B(-1,0).
(1)求二次函数的解析式;
(2)填空:要使该二次函数的图象与x轴只有一个交点,应把图象沿y轴向上平移
▲ 个单位.
解:(1)由已知,有,即,解得
∴所求的二次函数的解析式为. …………………………………………6分
(2) 4 …………………………………………………………………………………………2分
25.(2010年长沙)已知:二次函数的图象经过点(1,0),一次函数图象经过原点和点(1,-b),其中且、为实数.
(1)求一次函数的表达式(用含b的式子表示);
(2)试说明:这两个函数的图象交于不同的两点;
(3)设(2)中的两个交点的横坐标分别为x1、x2,求| x1-x2 |的范围.
解:(1)∵一次函数过原点∴设一次函数的解析式为y=kx
∵一次函数过(1,-b) ∴y=-bx ……………………………3分
(2)∵y=ax2+bx-2过(1,0)即a+b=2 …………………………4分
由得 ……………………………………5分
① ∵△=
∴方程①有两个不相等的实数根∴方程组有两组不同的解
∴两函数有两个不同的交点. ………………………………………6分
(3)∵两交点的横坐标x1、x2分别是方程①的解
∴
∴=
或由求根公式得出 ………………………………………………………8分
∵a>b>0,a+b=2 ∴2>a>1
令函数 ∵在1 0时,函数图象截x轴所得的线段长度大于;
③ 当m < 0时,函数在x >时,y随x的增大而减小;
④ 当m ¹ 0时,函数图象经过同一个点.
其中正确的结论有
A. ①②③④ B. ①②④ C. ①③④ D. ②④
答案:B
3、(2010年杭州市)在平面直角坐标系xOy中,抛物线的解析式是y =+1,
点C的坐标为(–4,0),平行四边形OABC的顶点A,B在抛物
线上,AB与y轴交于点M,已知点Q(x,y)在抛物线上,点
P(t,0)在x轴上.
(1) 写出点M的坐标;
(2) 当四边形CMQP是以MQ,PC为腰的梯形时.
① 求t关于x的函数解析式和自变量x的取值范围;
② 当梯形CMQP的两底的长度之比为1:2时,求t的值.
答案:
(1) ∵OABC是平行四边形,∴AB∥OC,且AB = OC = 4,
∵A,B在抛物线上,y轴是抛物线的对称轴,
∴ A,B的横坐标分别是2和– 2,
代入y = +1得, A(2, 2 ),B(– 2,2),
∴M(0,2)
(2) 过点Q作QH ^ x轴,设垂足为H, 则HQ = y ,HP = x–t ,
由△HQP∽△OMC,得: , 即: t = x – 2y ,
∵ Q(x,y) 在y = +1上, ∴ t = – + x –2.
当点P与点C重合时,梯形不存在,此时,t = – 4,解得x = 1± ,
当Q与B或A重合时,四边形为平行四边形,此时,x = ± 2
∴x的取值范围是x ¹ 1±, 且x¹± 2的所有实数
② 分两种情况讨论:
1)当CM > PQ时,则点P在线段OC上,
∵ CM∥PQ,CM = 2PQ ,
∴点M纵坐标为点Q纵坐标的2倍,即2 = 2( +1),解得x = 0 ,
∴t =–+ 0 –2 = –2
2)当CM < PQ时,则点P在OC的延长线上,
∵CM∥PQ,CM = PQ,
∴点Q纵坐标为点M纵坐标的2倍,即 +1=2´2,解得: x = ± .
当x = – 时,得t = – – –2 = –8 – ,
当x = 时, 得t = –8.
(2010陕西省)10.将抛物线C:y=x²+3x-10,将抛物线C平移到Cˋ。若两条抛物线C,Cˋ关于直线x=1对称,则下列平移方法中正确的是 (C)
A将抛物线C向右平移个单位 B将抛物线C向右平移3个单位
C将抛物线C向右平移5个单位 D将抛物线C向右平移6个单位
(2010陕西省)24.如图,在平面直角坐标系中,抛物线A(-1,0),B(3,0)C(0,-1)三点。
(1)求该抛物线的表达式;
(2)点Q在y轴上,点P在抛物线上,要使Q、P、A、B为顶点的四边形是平行四边形求所有满足条件点P的坐标。
解:(1)设该抛物线的表达式为y=ax²+bx+c根据题意,得
a- b+c=0 a=
9a+3b+c=0 解之,得 b=
c=-1 c=-1
∴所求抛物线的表达式为y=x²-x-1
(2)①AB为边时,只要PQ∥AB且PQ=AB=4即可。
又知点Q在y轴上,∴点P的横坐标为4或-4,这时符合条件的点P有两个,分别记为P1,P2 .
而当x=4时,y=;当x=-4时,y=7,
此时P1(4,)P2(-4,7)
②当AB为对角线时,只要线段PQ与线段AB互相平分即可
又知点Q在Y轴上,且线段AB中点的横坐标为1
∴点P的横坐标为2,这时符合条件的P只有一个记为P3
而且当x=2时y=-1 ,此时P3(2,-1)
综上,满足条件的P为P1(4,)P2(-4,7)P3(2,-1)
(2010年天津市)(10)已知二次函数()的图象如图所示,有下列结论:(D)
第(10)题
y
x
O
①;
②;
③;
④.
其中,正确结论的个数是
(A)1
(B)2
(C)3
(D)4
(2010年天津市)(16)已知二次函数()中自变量和函数值的部分对应值如下表:
…
0
1
…
…
0
…
则该二次函数的解析式为 .
(2010年天津市)(26)(本小题10分)
在平面直角坐标系中,已知抛物线与轴交于点、(点在点的左侧),与轴的正半轴交于点,顶点为.
(Ⅰ)若,,求此时抛物线顶点的坐标;
(Ⅱ)将(Ⅰ)中的抛物线向下平移,若平移后,在四边形ABEC中满足
S△BCE = S△ABC,求此时直线的解析式;
(Ⅲ)将(Ⅰ)中的抛物线作适当的平移,若平移后,在四边形ABEC中满足
S△BCE = 2S△AOC,且顶点恰好落在直线上,求此时抛物线的解析式.
解:解:(Ⅰ)当,时,抛物线的解析式为,即.
∴ 抛物线顶点的坐标为(1,4). .................2分
(Ⅱ)将(Ⅰ)中的抛物线向下平移,则顶点在对称轴上,有,
∴ 抛物线的解析式为().
∴ 此时,抛物线与轴的交点为,顶点为.
∵ 方程的两个根为,,
∴ 此时,抛物线与轴的交点为,.
E
y
x
F
B
D
A
O
C
如图,过点作EF∥CB与轴交于点,连接,则S△BCE = S△BCF.
∵ S△BCE = S△ABC,
∴ S△BCF = S△ABC.
∴ .
设对称轴与轴交于点,
则.
由EF∥CB,得.
∴ Rt△EDF∽Rt△COB.有.
∴ .结合题意,解得 .
∴ 点,.
设直线的解析式为,则
解得
∴ 直线的解析式为. .........................6分
(Ⅲ)根据题意,设抛物线的顶点为,(,)
则抛物线的解析式为,
此时,抛物线与轴的交点为,
与轴的交点为,.()
过点作EF∥CB与轴交于点,连接,
则S△BCE = S△BCF.
由S△BCE = 2S△AOC,
∴ S△BCF = 2S△AOC. 得.
设该抛物线的对称轴与轴交于点.
则 .
于是,由Rt△EDF∽Rt△COB,有.
∴ ,即.
结合题意,解得 . ①
∵ 点在直线上,有. ②
∴ 由①②,结合题意,解得.
有,.
∴ 抛物线的解析式为. .........................10分
(2010宁夏7.把抛物线向左平移1个单位,然后向上平移3个单位,则平移后抛物线的表达式 ( B )
A. B. C. D..
(2010山西23.(本题10分)已知二次函数y=x2-2x-3的图象与x轴交于A、B两点(A在B的左侧),与y轴交于点C,顶点为D.
(1)求点A、B、C、D的坐标,并在下面直角坐标系中画出该二次函数的大致图象;
(2)说出抛物线y=x2-2x-3可由抛物线y=x2如何平移得到?
(3)求四边形OCDB的面积.
1.(2010宁德)(本题满分12分)如图1,抛物线
与x轴交于A、C两点,与y轴交于B点,与直线交于A、D两点。
⑴直接写出A、C两点坐标和直线AD的解析式;
⑵如图2,质地均匀的正四面体骰子的各个面上依次标有数字-1、1、3、4.随机抛掷这枚骰子两次,把第一次着地一面的数字m记做P点的横坐标,第二次着地一面的数字n记做P点的纵坐标.则点落在图1中抛物线与直线围成区域内(图中阴影部分,含边界)的概率是多少?
图2
-1
3
y
x
0
D(5,-2)
C
B
A
图1
解:⑴ A点坐标:(-3,0),C点坐标:C(4,0);………………2分
直线AD解析式:.………………5分
⑵ 所有可能出现的结果如下(用列树状图列举所有可能同样得分):………………8分
第一次
第二次
-1
1
3
4
-1
(-1,-1)
(-1, 1)
(-1,3)
(-1,4)
1
(1,-1)
(1, 1)
(1,3)
(1,4)
3
(3,-1)
(3, 1)
(3, 3)
(3, 4)
4
(4,-1)
(4, 1)
(4, 3)
(4, 4)
总共有16种结果,每种结果出现的可能性相同,而落在
图1中抛物线与直线围成区域内的结果有7种:
(-1,1),(1,-1),(1,1),(1,3),(3,-1),(3,1),(4,-1). …………11分
因此P(落在抛物线与直线围成区域内)=.………………12分
(注:落在抛物线与直线围成区域内的点列举错误1个扣1分,2个及2个以上扣2分。由点列举错误引起概率计算错误不扣分。)
2.(2010宁德)(本题满分13分)如图,在梯形ABCD中,AD∥BC,∠B=90°,BC=6,AD=3,∠DCB=30°.点E、F同时从B点出发,沿射线BC向右匀速移动.已知F点移动速度是E点移动速度的2倍,以EF为一边在CB的上方作等边△EFG.设E点移动距离为x(x>0).
⑴△EFG的边长是____(用含有x的代数式表示),当x=2时,点G的位置在_______;
⑵若△EFG与梯形ABCD重叠部分面积是y,求
①当0<x≤2时,y与x之间的函数关系式;
②当2<x≤6时,y与x之间的函数关系式;
B E→ F→ C
A D
G
⑶探求⑵中得到的函数y在x取含何值时,存在最大值,并求出最大值.
解:⑴ x,D点;………………3分
⑵ ①当0<x≤2时,△EFG在梯形ABCD内部,所以y=x2;………………6分
②分两种情况:
Ⅰ.当2<x<3时,如图1,点E、点F在线段BC上,
△EFG与梯形ABCD重叠部分为四边形EFNM,
∵∠FNC=∠FCN=30°,∴FN=FC=6-2x.∴GN=3x-6.
由于在Rt△NMG中,∠G=60°,
所以,此时 y=x2-(3x-6)2=.………………9分
Ⅱ.当3≤x≤6时,如图2,点E在线段BC上,点F在射线CH上,
△EFG与梯形ABCD重叠部分为△ECP,
∵EC=6-x,
∴y=(6-x)2=.………………11分
⑶当0<x≤2时,∵y=x2在x>0时,y随x增大而增大,
∴x=2时,y最大=;
当2<x<3时,∵y=在x=时,y最大=;
当3≤x≤6时,∵y=在x<6时,y随x增大而减小,
∴x=3时,y最大=.………………12分
B E C F
A D
G
P
H
图2
综上所述:当x=时,y最大=.………………13分
B E F C
A D
G
N
M
图1
3(2010黄冈)若函数,则当函数值y=8时,自变量x的值是(D )
A.± B.4 C.±或4 D.4或-
4. (2010黄冈)(11分)某同学从家里出发,骑自行车上学时,速度v(米/秒)与时间t(秒)的关系如图a,A(10,5),B(130,5),C(135,0).
(1)求该同学骑自行车上学途中的速度v与时间t的函数关系式;
(2)计算该同学从家到学校的路程(提示:在OA和BC段的运动过程中的平均速度分别等于它们中点时刻的速度,路程=平均速度×时间);
(3)如图b,直线x=t(0≤t≤135),与图a的图象相交于P、Q,用字母S表示图中阴影部分面积,试求S与t的函数关系式;
(4)由(2)(3),直接猜出在t时刻,该同学离开家所超过的路程与此时S的数量关系.
图a 图b
解:(1)
(2)2.5×10+5×120+2×5=635(米)
(3)
(4) 相等的关系
5. (15分)已知抛物线顶点为C(1,1)且过原点O.过抛物线上一点P(x,y)向直线作垂线,垂足为M,连FM(如图).
(1)求字母a,b,c的值;
(2)在直线x=1上有一点,求以PM为底边的等腰三角形PFM的P点的坐标,并证明此时△PFM为正三角形;
(3)对抛物线上任意一点P,是否总存在一点N(1,t),使PM=PN恒成立,若存在请求出t值,若不存在请说明理由.
解:(1)a=-1,b=2,c=0
(2)过P作直线x=1的垂线,可求P的纵坐标为,横坐标为.此时,MP=MF=PF=1,故△MPF为正三角形.
(3)不存在.因为当t<,x<1时,PM与PN不可能相等,同理,当t>,x>1时,PM与PN不可能相等.
第10题图
y
x
O
-1
2
1.(2010山东济南)二次函数的图象如图所示,则函数值y<0时
x的取值范围是
A.x<-1
B.x>2
C.-1<x<2
D.x<-1或x>2
答案:C
2.(2010山东济南 )
如图所示,抛物线与x轴交于A、B两点,直线BD的函数表达式为,抛物线的对称轴l与直线BD交于点C、与x轴交于点E.
⑴求A、B、C三个点的坐标.
⑵点P为线段AB上的一个动点(与点A、点B不重合),以点A为圆心、以AP为半径的圆弧与线段AC交于点M,以点B为圆心、以BP为半径的圆弧与线段BC交于点N,分别连接AN、BM、MN.
①求证:AN=BM.
D
C
M
N
O
A
B
P
l
第24题图
y
E
②在点P运动的过程中,四边形AMNB的面积有最大值还是有最小值?并求出该最大值或最小值.
答案:.解:⑴令,
解得:,
∴A(-1,0),B(3,0) 2分
∵=,
∴抛物线的对称轴为直线x=1,
将x=1代入,得y=2,
∴C(1,2). 3分
⑵①在Rt△ACE中,tan∠CAE=,
∴∠CAE=60º,
由抛物线的对称性可知l是线段AB的垂直平分线,
∴AC=BC,
∴△ABC为等边三角形, 4分
∴AB= BC =AC = 4,∠ABC=∠ACB= 60º,
又∵AM=AP,BN=BP,
∴BN = CM,
∴△ABN≌△BCM,
∴AN=BM. 5分
②四边形AMNB的面积有最小值. 6分
设AP=m,四边形AMNB的面积为S,
由①可知AB= BC= 4,BN = CM=BP,S△ABC=×42=,
∴CM=BN= BP=4-m,CN=m,
过M作MF⊥BC,垂足为F,
则MF=MC•sin60º=,
∴S△CMN==•=, 7分
∴S=S△ABC-S△CMN
=-()
= 8分
∴m=2时,S取得最小值3. 9分
3.(2010昆明)在平面直角坐标系中,抛物线经过O(0,0)、A(4,0)、B(3,)三点.
(1)求此抛物线的解析式;
(2)以OA的中点M为圆心,OM长为半径作⊙M,在(1)中的抛物线上是否存在这样的点P,过点P作⊙M的切线l ,且l与x轴的夹角为30°,若存在,请求出此时点P的坐标;若不存在,请说明理由.(注意:本题中的结果可保留根号)
答案: 解:(1)设抛物线的解析式为:
由题意得: ……………1分
解得: ………………2分
∴抛物线的解析式为: ………………3分
l′
(2)存在 ………………4分
抛物线的顶点坐标是,作抛物线和⊙M(如图),
设满足条件的切线 l 与 x 轴交于点B,与⊙M相切于点C
连接MC,过C作CD⊥ x 轴于D
∵ MC = OM = 2, ∠CBM = 30°, CM⊥BC
∴∠BCM = 90° ,∠BMC = 60° ,BM = 2CM = 4 , ∴B (-2, 0)
在Rt△CDM中,∠DCM = ∠CDM - ∠CMD = 30°
∴DM = 1, CD = = ∴ C (1, )
设切线 l 的解析式为:,点B、C在 l 上,可得:
解得:
∴切线BC的解析式为:
∵点P为抛物线与切线的交点
由 解得:
∴点P的坐标为:, ………………8分
∵ 抛物线的对称轴是直线
此抛物线、⊙M都与直线成轴对称图形
于是作切线 l 关于直线的对称直线 l′(如图)
得到B、C关于直线的对称点B1、C1
l′满足题中要求,由对称性,得到P1、P2关于直线的对称点:
,即为所求的点.
∴这样的点P共有4个:,,, ………12
分
(本题其它解法参照此标准给分)
1.(2010山东德州)
为迎接第四届世界太阳城大会,德州市把主要路段路灯更换为太阳能路灯.已知太阳能路灯售价为5000元/个,目前两个商家有此产品.甲商家用如下方法促销:若购买路灯不超过100个,按原价付款;若一次购买100个以上,且购买的个数每增加一个,其价格减少10元,但太阳能路灯的售价不得低于3500元/个.乙店一律按原价的80℅销售.现购买太阳能路灯x个,如果全部在甲商家购买,则所需金额为y1元;如果全部在乙商家购买,则所需金额为y2元.
(1)分别求出y1、y2与x之间的函数关系式;
(2)若市政府投资140万元,最多能购买多少个太阳能路灯?
2.(2010四川宜宾)
将直角边长为6的等腰Rt△AOC放在如图所示的平面直角坐标系中,点O为坐标原点,点C、A分别在x、y轴的正半轴上,一条抛物线经过点A、C及点B(–3,0).
(1)求该抛物线的解析式;
(2)若点P是线段BC上一动点,过点P作AB的平行线交AC于点E,连接AP,当△APE的面积最大时,求点P的坐标;
24题图
(3)在第一象限内的该抛物线上是否存在点G,使△AGC的面积与(2)中△APE的最大面积相等?若存在,请求出点G的坐标;若不存在,请说明理由.
3.(2010山东德州)
已知二次函数的图象经过点A(3,0),B(2,-3),C(0,-3).
(1)求此函数的解析式及图象的对称轴;
(2)点P从B点出发以每秒0.1个单位的速度沿线段BC向C点运动,点Q从O点出发以相同的速度沿线段OA向A点运动,其中一个动点到达端点时,另一个也随之停止运动.设运动时间为t秒.
①当t为何值时,四边形ABPQ为等腰梯形;
x
y
O
A
B
C
P
Q
M
N
第23题图
②设PQ与对称轴的交点为M,过M点作x轴的平行线交AB于点N,设四边形ANPQ的面积为S,求面积S关于时间t的函数解析式,并指出t的取值范围;当t为何值时,S有最大值或最小值.
答案:1、解:(1)由题意可知,
当x≤100时,购买一个需元,故;-------------------1分
当x≥100时,因为购买个数每增加一个,其价格减少10元,但售价不得低于3500元/个,所以x≤+100=250. ------------------------2分
即100≤x≤250时,购买一个需5000-10(x-100)元,故y1=6000x-10x2;----------4分
当x>250时,购买一个需3500元,故; ----------------5分
所以,
. -------------------------------7分
(2) 当0MN成立的x的取值范围。
解:(1)∠ABE=∠CBD=30°
在△ABE中,AB=6
BC=BE=
CD=BCtan30°=4
∴OD=OC-CD=2
∴B(,6) D(0,2)
设BD所在直线的函数解析式是y=kx+b
∴
所以BD所在直线的函数解析式是
(2)∵EF=EA=ABtan30°= ∠FEG=180°-∠FEB-∠AEB=60°
又∵FG⊥OA
∴FG=EFsin60°=3 GE=EFcos60°= OG=OA-AE-GE=
又H为FG中点
∴H(,) …………4分
∵B(,6) 、 D(0,2)、 H(,)在抛物线图象上
∴
∴抛物线的解析式是
(2)∵MP=
MN=6-
H=MP-MN=
由得
该函数简图如图所示:
当00,即HP>MN
(苏州2010中考题29).(本题满分9分)如图,以A为顶点的抛物线与y轴交于点B.已知A、B两点的坐标分别为(3,0)、(0,4).
(1)求抛物线的解析式;
(2)设M(m,n)是抛物线上的一点(m、n为正整数),且它位于对称轴的右侧.若以M、B、O、A为顶点的四边形四条边的长度是四个连续的正整数,求点M的坐标;
(3)在(2)的条件下,试问:对于抛物线对称轴上的任意一点P,PA2+PB2+PM2>28是
否总成立?请说明理由.
答案:
(益阳市2010年中考题20).如图9,在平面直角坐标系中,已知A、B、C三点的坐标分别为A(-2,0),B(6,0),C(0,3).
(1)求经过A、B、C三点的抛物线的解析式;
(2)过C点作CD平行于轴交抛物线于点D,写出D点的坐标,并求AD、BC的交点E的坐标;
(3)若抛物线的顶点为P,连结PC、PD,判断四边形CEDP的形状,并说明理由.
20.解:⑴ 由于抛物线经过点,可设抛物线的解析式为,则,
解得
∴抛物线的解析式为 ……………………………4分
⑵ 的坐标为 ……………………………5分
直线的解析式为
直线的解析式为
由
求得交点的坐标为 ……………………………8分
⑶ 连结交于,的坐标为
又∵,
∴,且
∴四边形是菱形 ……………………………12分
x
(第9题图)
y
O
9. (莱芜)二次函数的图象如图所示,则一次函
数的图象不经过( D )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
(第24题图)
x
y
O
A
C
B
D
E
F
24. (莱芜)如图,在平面直角坐标系中,已知抛物线交轴于两点,交轴于点.
(1)求此抛物线的解析式;
(2)若此抛物线的对称轴与直线交于点D,作
⊙D与x轴相切,⊙D交轴于点E、F两点,求劣弧
EF的长;
(3)P为此抛物线在第二象限图像上的一点,PG垂直
于轴,垂足为点G,试确定P点的位置,使得△PGA
的面积被直线AC分为1︰2两部分.
解:(1)∵抛物线经过点,,.
∴, 解得.
∴抛物线的解析式为:. …………………………3分
(2)易知抛物线的对称轴是.把x=4代入y=2x得y=8,∴点D的坐标为(4,8).
∵⊙D与x轴相切,∴⊙D的半径为8. …………………………4分
连结DE、DF,作DM⊥y轴,垂足为点M.
在Rt△MFD中,FD=8,MD=4.∴cos∠MDF=.
∴∠MDF=60°,∴∠EDF=120°. …………………………6分
∴劣弧EF的长为:. …………………………7分
(3)设直线AC的解析式为y=kx+b. ∵直线AC经过点.
∴,解得.∴直线AC的解析式为:. ………8分
设点,PG交直线AC于N,
则点N坐标为.∵.
x
y
O
A
C
B
D
E
F
P
G
N
M
∴①若PN︰GN=1︰2,则PG︰GN=3︰2,PG=GN.
即=.
解得:m1=-3, m2=2(舍去).
当m=-3时,=.
∴此时点P的坐标为. …………………………10分
②若PN︰GN=2︰1,则PG︰GN=3︰1, PG=3GN.
即=.
解得:,(舍去).当时,=.
∴此时点P的坐标为.
综上所述,当点P坐标为或时,△PGA的面积被直线AC分成1︰2两部分. …………………12分
1.(2010,安徽芜湖)二次函数y=ax2+bx+c的图像如图所示,反比例函数y=与正比例函数y=(b+c)x在同一坐标系中的大致图像可能是( )
【答案】B
2.(2010,浙江义乌)(1)将抛物线y1=2x2向右平移2个单位,得到抛物线y2的图象,则y2= ▲ ; (2)如图,P是抛物线y2对称轴上的一个动点,直线x=t平行于y轴,分别与直线y=x、抛物线y2交于点A、B.若△ABP是以点A或点B为直角顶点的等腰直角三角形,求满足条件的t的值,则t= ▲ .
P
y
x
·
【答案】2(x-2)2 或
3.(2010,安徽芜湖)用长度为20m的金属材料制成如图所示的金属框,下部为矩形,上部为等腰直角三角形,其斜边长为2xm,当该金属框围成的图形面积最大时,图形中矩形的相邻两边长各为多少?请求出金属框围成的图形的最大面积。
【答案】解:根据题意得:等腰直角三角形的直角边长为xm,矩形的一边长为2xm.
其相邻边长为
所以,该金属框围成的面积S=
= (0