中考抛物线图像题型 11页

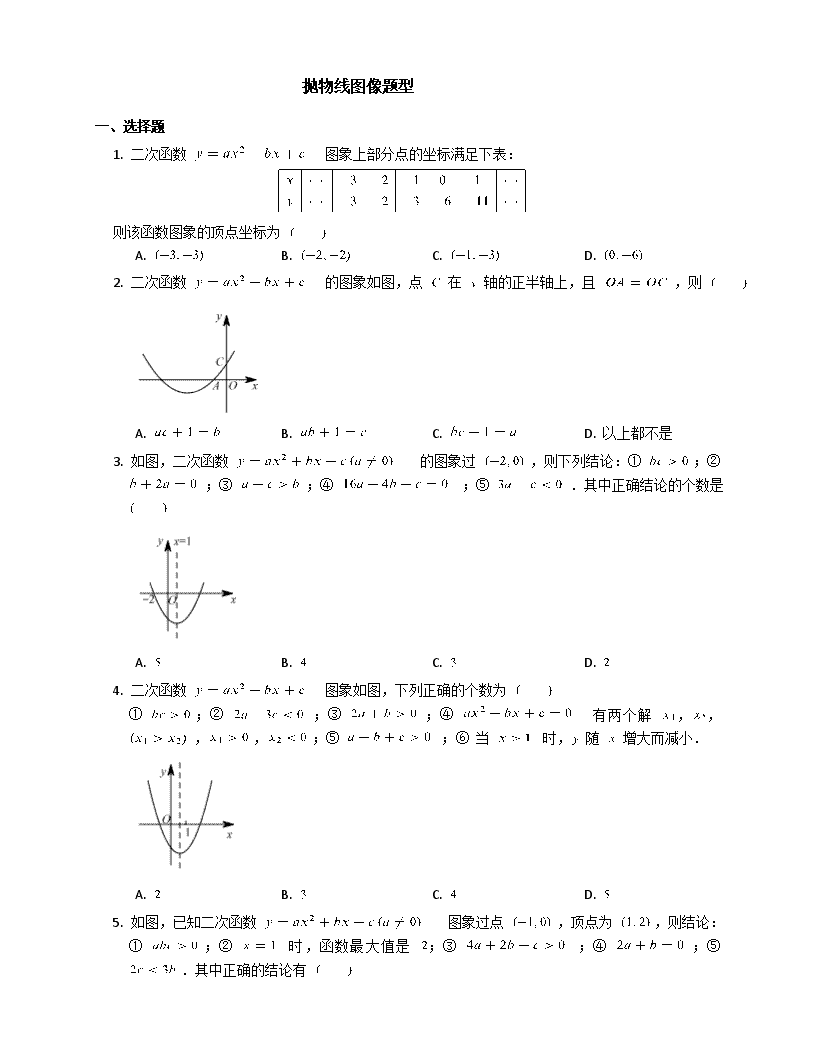
抛物线图像题型 ‎ ‎ 一、选择题 ‎1. 二次函数 图象上部分点的坐标满足下表：‎ 则该函数图象的顶点坐标为 ‎ ‎ A. B. C. D. ‎ ‎ ‎ ‎2. 二次函数 的图象如图，点 在 轴的正半轴上，且 ，则 ‎ ‎ ‎ ‎ A. B. C. D. 以上都不是 ‎ ‎ ‎3. 如图，二次函数 的图象过 ，则下列结论：① ；② ；③ ；④ ；⑤ ．其中正确结论的个数是 ‎ ‎ ‎ ‎ A. B. C. D. ‎ ‎ ‎ ‎4. 二次函数 图象如图，下列正确的个数为 ‎ ‎ ① ；② ；③ ；④ 有两个解 ，，，，；⑤ ；⑥ 当 时， 随 增大而减小．‎ ‎ ‎ ‎ A. B. C. D. ‎ ‎ ‎ ‎5. 如图，已知二次函数 图象过点 ，顶点为 ，则结论：‎ ‎ ① ；② 时，函数最大值是 ；③ ；④ ；⑤ ．其中正确的结论有 ‎ ‎ ‎ ‎ A. 个 B. 个 C. 个 D. 个 ‎ ‎ ‎6. 如图是抛物线 的部分图象，其顶点坐标为 ，且与 轴的一个交点在点 和 之间，则下列结论：‎ ‎ ① ；‎ ‎ ② ；‎ ‎ ③ ；‎ ‎ ④一元二次方程 有两个不相等的实根．‎ ‎ 其中正确结论的个数是 ‎ ‎ ‎ ‎ A. 个 B. 个 C. 个 D. 个 ‎ ‎ ‎7. 如图，抛物线 的对称轴为直线 ，与 轴的一个交点坐标为 ，其部分图象如图所示，下列结论：‎ ‎ ① ；‎ ‎ ②方程 的两个根是 ，；‎ ‎ ③ ；‎ ‎ ④当 时， 的取值范围是 ；‎ ‎ ⑤当 时， 随 增大而增大；‎ ‎ 其中结论正确的个数是 ‎ ‎ ‎ ‎ A. 个 B. 个 C. 个 D. 个 ‎ ‎ ‎8. 已知抛物线 的顶点为 ，与 轴的一个交点在 和 之间，其部分图象如图，则以下结论：‎ ‎ ；‎ ‎ ；‎ ‎ ；‎ ‎ 方程 一定有实数根，‎ ‎ 其中正确的结论为 ‎ ‎ ‎ ‎ A. B. C. D. 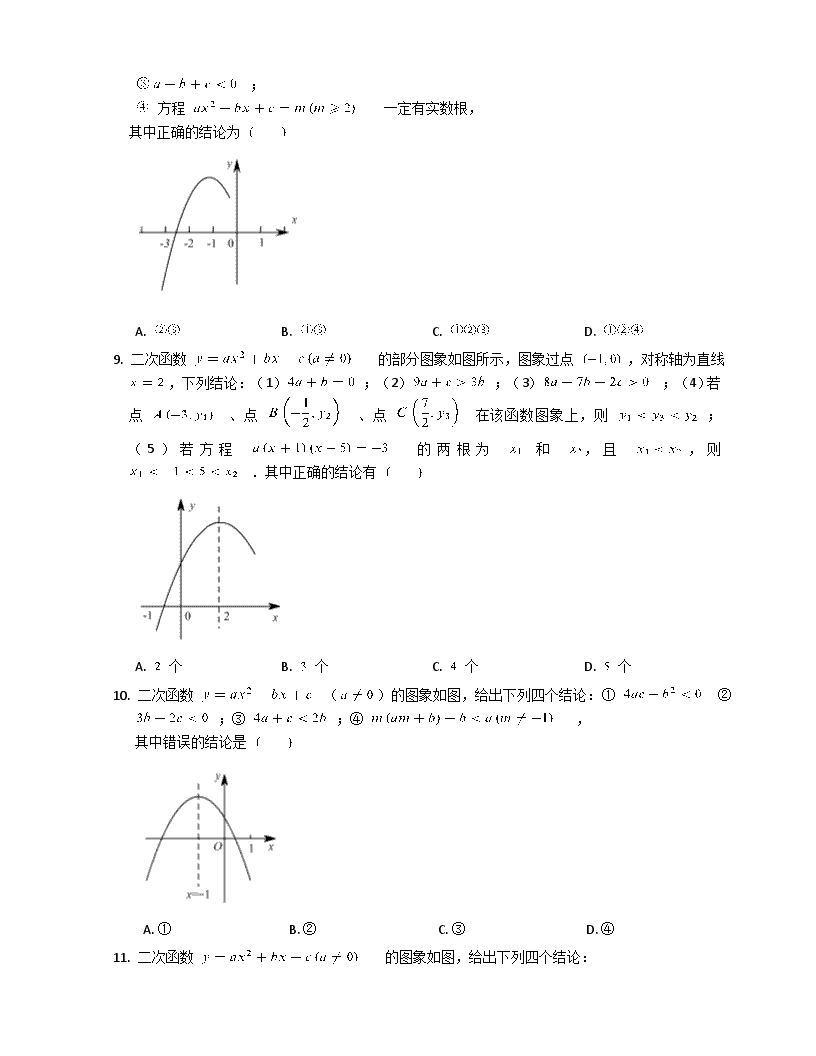‎ ‎ ‎ ‎9. 二次函数 的部分图象如图所示，图象过点 ，对称轴为直线 ，下列结论：（1）；（2）；（3）；（4）若点 、点 、点 在该函数图象上，则 ；（5）若方程 的两根为 和 ，且 ，则 ．其中正确的结论有 ‎ ‎ ‎ ‎ A. 个 B. 个 C. 个 D. 个 ‎ ‎ ‎10. 二次函数 （）的图象如图，给出下列四个结论：① ② ；③ ；④ ，‎ ‎ 其中错误的结论是 ‎ ‎ ‎ ‎ A. ① B. ② C. ③ D. ④‎ ‎ ‎ ‎11. 二次函数 的图象如图，给出下列四个结论：‎ ‎ ① ；‎ ‎ ② ；‎ ‎ ③ ；‎ ‎ ④ ．‎ ‎ 其中正确结论的个数是 ‎ ‎ ‎ ‎ A. 个 B. 个 C. 个 D. 个 ‎ ‎ 二、填空题 ‎12. 如图，抛物线 与 轴交于点 ，，下列判断：‎ ‎ ① ；② ；③ ；④ ．‎ ‎ 其中判断一定正确的序号是  ．‎ ‎ ‎ ‎ ‎ ‎13. 已知二次函数 的图象如图所示，则下列 个结论正确的有   个．‎ ‎ ① ；② ；③ ；④对于任意 均有 ；⑤ ；⑥ ；⑦当 时， 随着 的增大而减小．‎ ‎ ‎ ‎ ‎ ‎14. 如图，是二次函数 的图象的一部分，给出下列命题：① ；② ；③ 的两根分别为 和 ；④ ．其中正确的命题是  ．（只要求填写正确命题的序号）‎ ‎ ‎ ‎ ‎ ‎15. 小明从二次函数 的图象（如图）中观察得出了下面五条信息：① ；② ；③ ；④ ；⑤ ．你认为其中正确的信息是   .‎ ‎ ‎ ‎ ‎ 三、解答题 ‎16. 如图，已知抛物线 与一直线相交于 ， 两点，与 轴交于点 ．其顶点为 ．‎ ‎ ‎ ‎（1）抛物线及直线 的函数关系式；‎ ‎（2）设点 ，求使 的值最小时 的值；‎ ‎（3）若抛物线的对称轴与直线 相交于点 ， 为直线 上的任意一点，过点 作 交抛物线于点 ，以 ，，， 为顶点的四边形能否为平行四边形?若能，求点 的坐标；若不能，请说明理由．‎ 答案 第一部分 ‎1. B 2. A 3. B 4. B 【解析】 抛物线开口向上，‎ ‎ ，‎ ‎ 对称轴在 轴右侧，‎ ‎ ， 异号即 ，‎ ‎ 抛物线与 轴的交点在负半轴，‎ ‎ ，所以 ，故①正确．‎ ‎ ② ，，‎ ‎ ，故②错误．‎ ‎ ③ 对称轴 ，，‎ ‎ ，‎ ‎ ，故③正确．‎ ‎④ 二次函数 的图象与 轴的两个交点分别在原点的左右两侧，即方程 有两个解 ，，当 时，，，故④正解．‎ ‎⑤由图形可知 时，，故⑤错误．‎ ‎⑥ ，对称轴 ，‎ ‎ 当 时， 随 增大而增大，故⑥错误．‎ 综上所述，正确的结论是①③④，共 个．‎ ‎5. C ‎ ‎6. C 7. B 8. C 【解析】因为抛物线与 轴有两个交点，‎ 所以 ，所以 正确；‎ 因为抛物线的顶点为 ，‎ 所以 ，‎ 因为抛物线的对称轴为直线 ，‎ 所以 ，‎ 所以 ，即 ，所以 正确；‎ 因为抛物线的对称轴为直线 ，‎ 因为抛物线与 轴的一个交点 在点 和 之间，‎ 所以抛物线与 轴的另一个交点在点 和 之间，‎ 所以当 时，，‎ 所以 ，所以 正确；‎ 因为抛物线的顶点为 ，‎ 因为当 时，二次函数有最大值为 ，‎ 所以方程 有两个相等的实数根，‎ 因为 ，‎ 所以方程 没有实数根，所以 错误 ‎9. B 【解析】（1）正确．‎ ‎ ，‎ ‎ ．‎ ‎（2）错误．‎ ‎ 时，，‎ ‎ ，‎ ‎ ．‎ ‎（3）正确．‎ 由图象可知抛物线经过 和 ，‎ ‎ ‎ 解得 ‎ ‎ ，‎ ‎ ，‎ ‎ ．‎ ‎（4）错误．‎ ‎ 点 、点 、点 ，‎ ‎ ，，‎ ‎ ，‎ ‎ 点 离对称轴的距离近，‎ ‎ ，‎ ‎ ，，‎ ‎ ，‎ ‎ ．‎ ‎（5）正确．‎ ‎ ，‎ ‎ ，‎ 即 ，‎ 故 或 ．‎ ‎ 正确的有三个．‎ ‎10. C ‎ ‎【解析】①根据图象与 轴有 个交点，可知 ，①正确；‎ ‎ ②根据 时， 和对称轴是 ，‎ 可知 ，，②正确；‎ ‎ ③根据 时，，可知 ，③错误；‎ ‎ ④根据当 时， 有最大值 ，‎ 可知 ，，④正确．‎ ‎11. B 【解析】∵抛物线和 轴有两个交点，‎ ‎∴ ，‎ ‎∴ ．‎ ‎∵对称轴是直线 ，和 轴的一个交点在点 和点 之间，‎ ‎∴抛物线和 轴的另一个交点在 和 之间，‎ ‎∴把 代入抛物线得：，‎ ‎∴ ．‎ ‎∵把 代入抛物线得：，‎ ‎∴ ，‎ ‎∵ ，‎ ‎∴ ，∴③正确；‎ ‎∵抛物线的对称轴是直线 ，‎ ‎∴ 的值最大，‎ 即把 代入得：，‎ ‎∴ ，‎ 即 ．‎ 第二部分 ‎12. ①②‎ ‎13. ‎ ‎14. ①③‎ ‎【解析】图象过点 故①正确；根据函数对称轴可知②错误，③正确；函数图象开口向上则 ，故④错误 ‎15. ①②③⑤‎ ‎【解析】 抛物线开口方向向上，‎ ‎ ．‎ ‎ 与 轴交点在 轴的下方，‎ ‎ ．‎ ‎ ，‎ ‎ ．‎ ‎ ，‎ ‎ ．‎ ‎ ，．‎ 由此看来①②是正确的，而④是错误的；‎ 当 ，，‎ 而点 在第二象限，‎ ‎③ 是正确的；‎ 当 时，，‎ 而点 在第一象限，‎ ‎ ⑤ 正确．‎ 第三部分 ‎16. （1） 由抛物线 过点 及 ，得 ‎ 解得 ‎ ‎ 抛物线为 ．‎ 设直线为 ，过点 及 得 ‎ ‎ 解得 ‎ ‎ 直线 为 ．‎ ‎      （2） 作 点关于直线 的对称点 ．则 ，连接 ．‎ 由（1）得 ，‎ ‎ 直线 的函数关系式为 ．‎ 当 在直线 上时， 的值最小，则 ．‎ ‎      （3） 由（1），（2）得 ，．‎ ‎ 点 在直线 上，设 ．‎ ‎（i）当点 在线段 上时，点 在点 上方，则 ．‎ ‎ 在抛物线上，‎ ‎ ，‎ 解得 或 ．‎ ‎ ．‎ ‎（ii）当点 在线段 （或 ）延长线上时，点 在点 下方，则 ，由 在抛物线上，‎ ‎ ．‎ 解得 或 ．‎ ‎ 或 ．‎ 满足条件的点 为 或 或 ．‎