中考二次函数与几何综合专题复习 2页

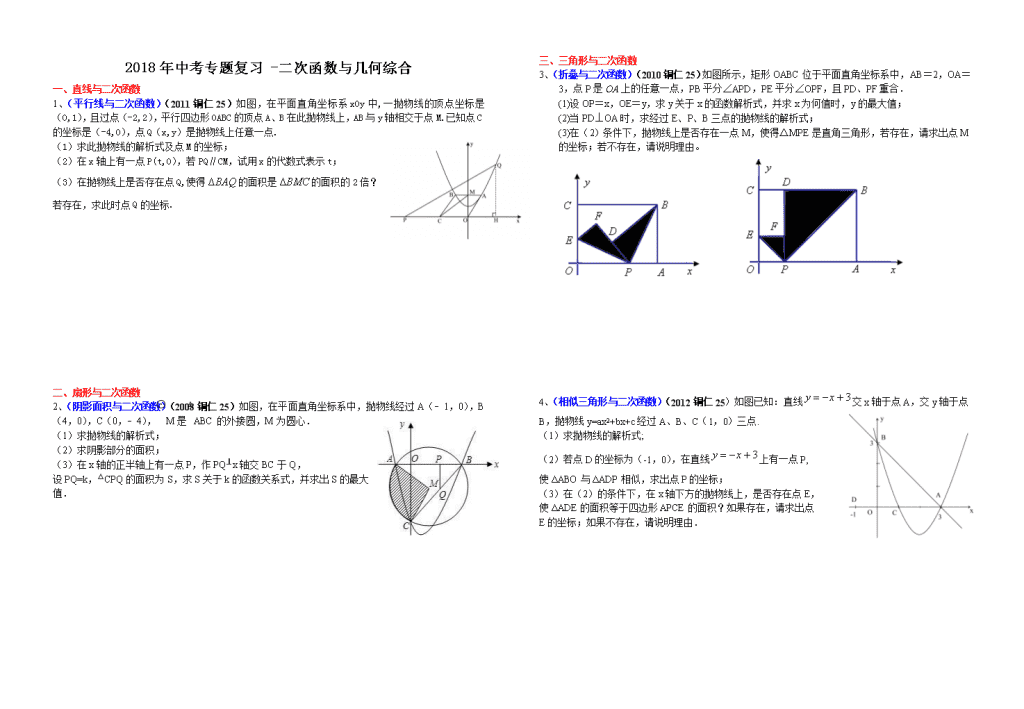
‎2018年中考专题复习 -二次函数与几何综合 一、直线与二次函数 ‎1、（平行线与二次函数）（2011铜仁25）如图，在平面直角坐标系xOy中,一抛物线的顶点坐标是（0,1），且过点（-2,2），平行四边形OABC的顶点A、B在此抛物线上，AB与y轴相交于点M.已知点C的坐标是（-4,0），点Q（x,y）是抛物线上任意一点.‎ ‎（1）求此抛物线的解析式及点M的坐标；‎ ‎（2）在x轴上有一点P(t,0），若PQ∥CM，试用x的代数式表示t；‎ ‎（3）在抛物线上是否存在点Q,使得的面积是的面积的2倍？‎ 若存在，求此时点Q的坐标.‎ 二、扇形与二次函数 ‎2、（阴影面积与二次函数）（2008铜仁25）如图，在平面直角坐标系中，抛物线经过A（﹣1，0），B（4，0），C（0，﹣4），⊙M是△ABC的外接圆，M为圆心．‎ ‎（1）求抛物线的解析式；‎ ‎（2）求阴影部分的面积；‎ ‎（3）在x轴的正半轴上有一点P，作PQ⊥x轴交BC于Q，‎ 设PQ=k，△CPQ的面积为S，求S关于k的函数关系式，并求出S的最大值．‎ 三、三角形与二次函数 ‎3、（折叠与二次函数）（2010铜仁25）如图所示，矩形OABC位于平面直角坐标系中，AB＝2，OA＝3，点P是OA上的任意一点，PB平分∠APD，PE平分∠OPF，且PD、PF重合．‎ ‎(1)设OP＝x，OE＝y，求y关于x的函数解析式，并求x为何值时，y的最大值；‎ ‎(2)当PD⊥OA时，求经过E、P、B三点的抛物线的解析式；‎ ‎(3)在（2）条件下，抛物线上是否存在一点M，使得△MPE是直角三角形，若存在，请求出点M的坐标；若不存在，请说明理由。‎ ‎ ‎ ‎4、（相似三角形与二次函数）（2012铜仁25）如图已知：直线交x轴于点A，交y轴于点B，抛物线y=ax2+bx+c经过A、B、C（1，0）三点.‎ ‎（1）求抛物线的解析式;‎ ‎（2）若点D的坐标为（-1，0），在直线上有一点P,‎ 使ΔABO与ΔADP相似，求出点P的坐标；‎ ‎（3）在（2）的条件下，在x轴下方的抛物线上，是否存在点E，‎ 使ΔADE的面积等于四边形APCE的面积？如果存在，请求出点 E的坐标；如果不存在，请说明理由．‎ ‎ ‎ ‎5、（等腰三角形与二次函数）（2013铜仁25）如图，已知直线y=3x-3分别交x轴、y轴于A、B两点，抛物线y=x2+bx+c经过 A、B两点，点C是抛物线与x轴的另一个交点(与A点不重合)．‎ ‎ (1)求抛物线的解析式：‎ ‎ (2)求△ABC的面积；‎ ‎ (3)在抛物线的对称轴上，是否存在点M，使△ABM为等腰三角形?‎ 若不存在，请说明理由：若存在，求出点M的坐标.‎ 三、动点与二次函数 ‎6、（2015•铜仁）如图，关于x的二次函数y=x2+bx+c的图象与x轴交于点A（1，0）和点B与y轴交于点C（0，3），抛物线的对称轴与x轴交于点D．‎ ‎（1）求二次函数的表达式；‎ ‎（2）在y轴上是否存在一点P，使△PBC为等腰三角形？若存在．请求出点P的坐标）；‎ ‎（3）有一个点M从点A出发，以每秒1个单位的速度在AB上向点B运动，另一个点N从点D与点M同时出发，以每秒2个单位的速度在抛物线的对称轴上运动，当点M到达点B时，点M、N同时停止运动，问点M、N运动到何处时，△MNB面积最大，试求出最大面积．‎ 四、周长与二次函数 ‎7、（2016•铜仁）如图，抛物线y=ax2+bx-1(a≠0)经过A(-1，0),B(2，0)两点，与y轴交于点C。 ‎ ‎(1)求抛物线的解析式及顶点D的坐标；‎ ‎(2)点P在抛物线的对称轴上，当△ACP的周长最小时，求出点P的坐标；‎ ‎(3) 点N在抛物线上，点M在抛物线的对称轴上，是否存在以点N为直角顶点的Rt△DNM与Rt△BOC相似，若存在，请求出所有符合条件的点N的坐标；若不存在，请说明理由。‎ 五、作图与二次函数 ‎8．（2017•铜仁）如图，抛物线y=x2+bx+c经过点A（﹣1，0），B（0，﹣2），并与x轴交于点C，点M是抛物线对称轴l上任意一点（点M，B，C三点不在同一直线上）．‎ ‎（1）求该抛物线所表示的二次函数的表达式；‎ ‎（2）在抛物线上找出两点P1，P2，使得△MP1P2与△MCB全等，并求出点P1，P2的坐标；‎ ‎（3）在对称轴上是否存在点Q，使得∠BQC为直角，若存在，作出点Q（用尺规作图，保留作图痕迹），并求出点Q的坐标．‎