上海中考数学模拟试卷2 4页

初三模拟测试数学试卷2‎ 一、选择题：（本大题共6题，每题4分，满分24分）‎ ‎1．4的平方根是 ‎ （A）2； （B）； （C）； （D）．‎ ‎2．下列等式中，一定成立的是 ‎ （A）； （B）；‎ ‎ （C）； （D）．‎ ‎3． 是下列哪个方程的解 ‎ （Ａ）； （Ｂ）；‎ ‎ （Ｃ）； （Ｄ）．‎ ‎4．已知点A (-2，3 )在双曲线上，则下列点中，一定在该双曲线上的点是 ‎ （A）A (3，-2 )； （B）A (-2，-3 )； （C）A (2，3 )； （D）A (3，2) .‎ 5． 下列图形中，是旋转对称图形，但不是中心对称图形的是 ‎ （A）等腰梯形； （B）等边三角形； （C）平行四边形； （D）直角梯形．‎ ‎6.在研究圆的有关性质时，我们曾做过这样的一个操作“将一张圆形纸片沿着它的任意一条 直径翻折，可以看到直径两侧的两个半圆互相重合”。由此说明：‎ ‎ （Ａ）圆是中心对称图形，圆心是它的对称中心； ‎ ‎ （Ｂ）圆是轴对称图形，任意一条直径所在的直线都是它的对称轴；‎ ‎ （Ｃ）圆的直径互相平分； ‎ ‎ （Ｄ）垂直弦的直径平分弦及弦所对的弧．‎ 一、 填空题：（本大题共12题，每题4分，满分48分）‎ ‎1‎ x y O A (2,1)‎ ‎2‎ 图1‎ ‎7．计算：= ．‎ ‎8．因式分解：= . ‎ ‎9．方程的解为 .‎ ‎10．已知一次函数y=kx+b的图象经过点A（2，1）（如图1）， 当x 时，y≥1. 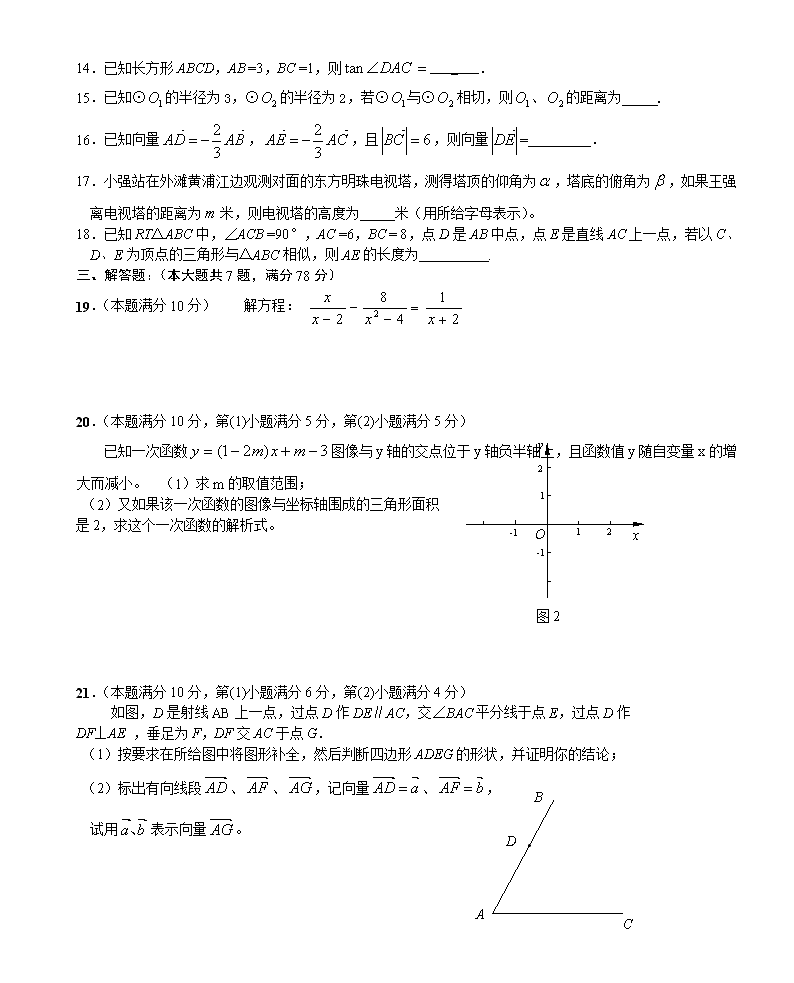‎ ‎11．从1、2、3、…… 9九个自然数中任选一个数，选出的数被2整除的概率是 .‎ ‎12．小明家离开学校的距离是a米，他上学时每分钟走b米，放学回家时每分钟比上学时少走 15米，则小明从学校回家用的时间是 分钟（用含a、b的代数式表示）．‎ ‎13．请你写出一个二次函数解析式，使其图像的顶点在轴上，且在轴右侧图像是下降的 ______________．‎ ‎14．已知长方形ABCD，AB =3，BC =1，则_______．‎ ‎15．已知⊙的半径为3，⊙的半径为2，若⊙与⊙相切，则、的距离为 .‎ ‎16．已知向量，，且，则向量= ．‎ ‎17．小强站在外滩黄浦江边观测对面的东方明珠电视塔，测得塔顶的仰角为，塔底的俯角为，如果王强离电视塔的距离为米，则电视塔的高度为 米（用所给字母表示）。‎ ‎18．已知RT△ABC中，∠ACB =90°，AC =6，BC = 8，点D是AB中点，点E是直线AC上一点，若以C、D、E为顶点的三角形与△ABC相似，则AE的长度为 .‎ 三、解答题：（本大题共7题，满分78分）‎ ‎19．（本题满分10分） 解方程： ‎ ‎20．（本题满分10分，第(1)小题满分5分，第(2)小题满分5分）‎ ‎ 已知一次函数图像与y轴的交点位于y轴负半轴上，且函数值y随自变量x的增大而减小。 图2‎ O y x ‎1‎ ‎2‎ ‎-1‎ ‎1‎ ‎-1‎ ‎2‎ （1）求m的取值范围；‎ ‎ （2）又如果该一次函数的图像与坐标轴围成的三角形面积 是2，求这个一次函数的解析式。‎ ‎ ‎ ‎21．（本题满分10分，第(1)小题满分6分，第(2)小题满分4分）‎ ‎ 如图，D是射线AB上一点，过点D作DE∥AC，交∠BAC平分线于点E，过点D作 DF⊥AE ，垂足为F，DF交AC于点G．‎ ‎ （1）按要求在所给图中将图形补全，然后判断四边形ADEG的形状，并证明你的结论；‎ C D B A ‎.‎ ‎ （2）标出有向线段、、，记向量、，‎ ‎ 试用表示向量。‎ ‎22、.汽车在行驶过程中，油箱中剩余的油量Q（升）与行驶里程s（千米）之间存在函数关系，其中、k为常数。小明乘坐爸爸驾驶的汽车（出发前刚加满油），他注意到当仪表显示行驶里程为200千米时，油箱中还有25升油；当仪表显示行驶里程为300千米时，油箱中还有15升油。又知当油箱中剩余的油量不足2升时，必须再次加油。试问这辆汽车加满油以后，最多可以行驶多少千米，就必须再次加油。‎ ‎23．（本题满分12分，第(1)小题满分6分，第(2)小题满分6分）‎ ‎ 如图，已知⊙、⊙交于点A、B，A、B的延长线分别与⊙交于点C、D，‎ ‎（1）求证：AC =BD ；D C B A 图6‎ （2）若⊙的半径为5，, ，求CD的长。‎ ‎24．（本题满分12分，第(1)小题满分6分，第(2)小题满分6分）‎ ‎ 在直角坐标系中，把点A（－1，a）（a为常数）向右平移4个单位得到点，经过点A、的抛物线与轴的交点的纵坐标为2． （1）求这条抛物线的解析式；‎ x y Ox 图7‎ ‎ （2）设该抛物线的顶点为点P，点B的坐标为，且，若△ABP是等腰三角形，求点B的坐标。‎ ‎ ‎ ‎25．（本题满分14分，第(1)小题满分3分，第(2)小题满分5分，第(3)小题满分6分）‎ 小杰和他的同学组成了“爱琢磨”学习小组，有一次，他们碰到这样一道题：‎ ‎“已知正方形ABCD ，点E、F、G、H分别在边AB、BC、CD、DA上，若EG⊥FH，则EG = FH”‎ ‎ 经过思考，大家给出了以下两个方案：‎ ‎（甲）过点A作AM∥HF交BC于点M，过点B作BN∥EG交CD于点N ；‎ ‎（乙）过点A作AM∥HF交BC于点M，作AN∥EG交CD的延长线于点N ；‎ ‎ 小杰和他的同学顺利地解决了该题后，大家琢磨着想改变问题的条件，作更多的探索。 ‎ ‎ ……‎ ‎ ‎ ‎]（1）对小杰遇到的问题，请在甲、乙两个方案中任选一个，加以证明（如图8）；‎ ‎（2）如果把条件中的“正方形”改为“长方形”，并设AB =2，BC =3（如图9），试探究EG、FH之间有怎样的数量关系，并证明你的结论；‎ ‎（3）如果把条件中的“EG⊥FH”改为“EG与FH的夹角为45°”，并假设正方形ABCD的边长为1，FH的长为（如图10），试求EG的长度。‎ H G F E D C B A ‎ 图10‎ H G F E D C B A ‎ 图9‎ ‎ 图8‎ H G F E D C B A