2014年江西省中考数学试题及答案 13页

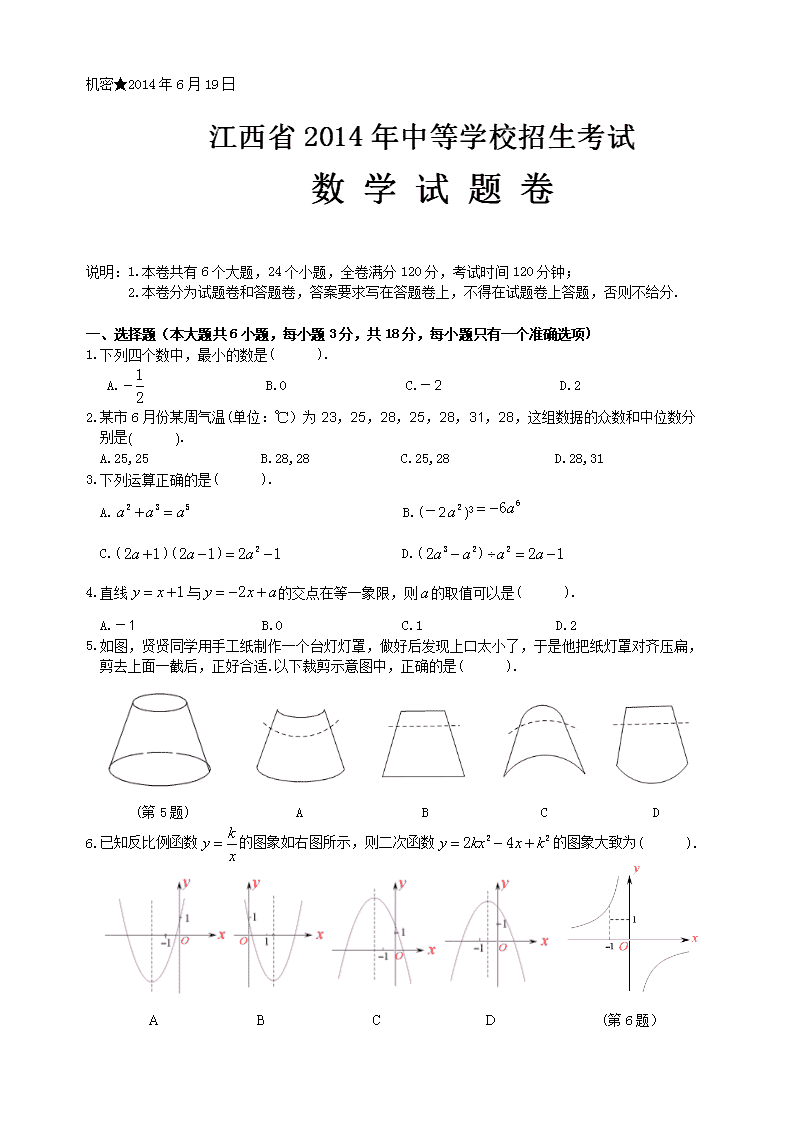
机密★‎‎2014年6月19日 ‎ 江西省2014年中等学校招生考试 数 学 试 题 卷 说明：1.本卷共有6个大题，24个小题，全卷满分120分，考试时间120分钟；‎ ‎ 2.本卷分为试题卷和答题卷，答案要求写在答题卷上，不得在试题卷上答题，否则不给分.‎ 一、 选择题（本大题共6小题，每小题3分，共18分，每小题只有一个准确选项)‎ ‎1.下列四个数中，最小的数是( ).‎ ‎ A. B‎.0 C.－2 D.2 ‎ 2. 某市6月份某周气温(单位：℃）为23，25，28，25，28，31，28，这组数据的众数和中位数分 别是( ).‎ ‎ A.25,25 B.28,‎28 C.25,28 D.28,31‎ 3. 下列运算正确的是( ).‎ ‎ A. B.(－2)3 ‎ ‎ C.()() D.()‎ 4. 直线与的交点在等一象限，则的取值可以是( ).‎ ‎ A.－1 B‎.0 C.1 D.2‎ 5. 如图，贤贤同学用手工纸制作一个台灯灯罩，做好后发现上口太小了，于是他把纸灯罩对齐压扁， 剪去上面一截后，正好合适.以下裁剪示意图中，正确的是( ).‎ ‎ ‎ ‎ (第5题) A B C D 6. 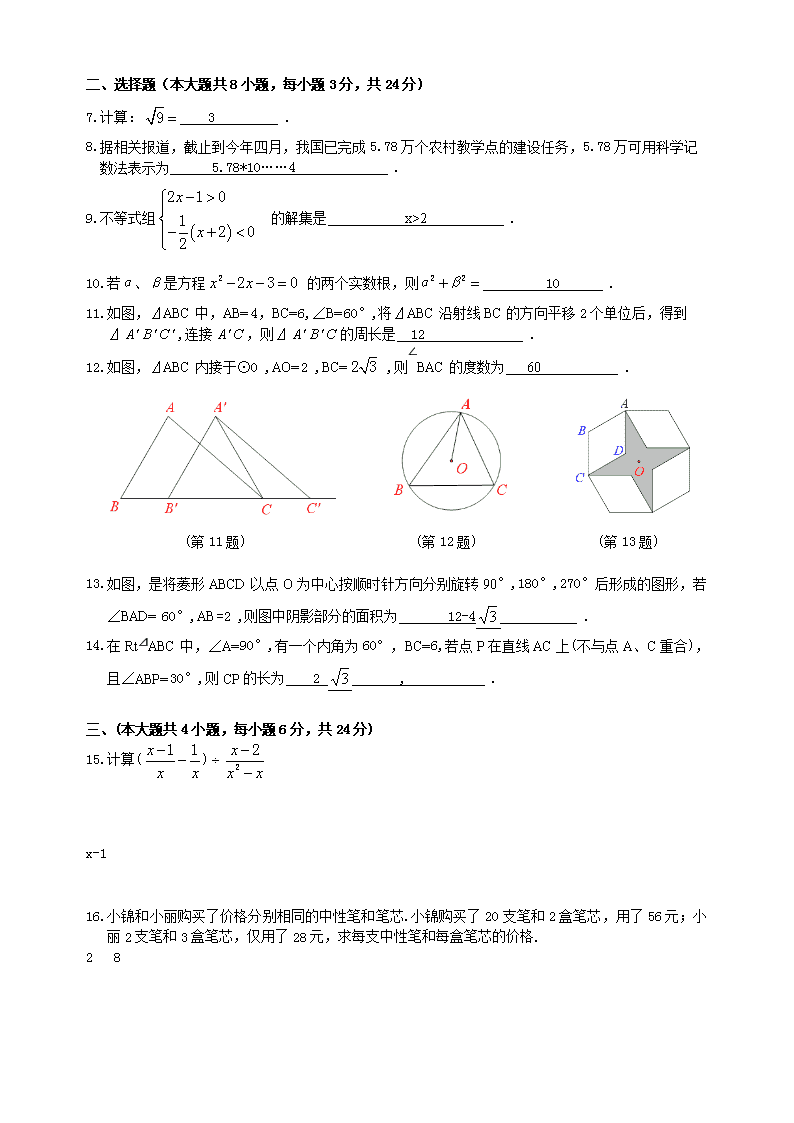已知反比例函数的图象如右图所示，则二次函数的图象大致为( ).‎ ‎ A B C D (第6题） ‎ 一、 选择题（本大题共8小题，每小题3分，共24分)‎ ‎7.计算： 3 .‎ ‎8.据相关报道，截止到今年四月，我国已完成5.78万个农村教学点的建设任务，5.78万可用科学记 ‎ 数法表示为 5.78*10……4 .‎ 9. 不等式组 的解集是 x>2 .‎ ‎10.若、是方程 的两个实数根，则 10 . ‎ ‎11.如图，⊿ABC中，AB=4，BC=6,∠B=60°,将⊿ABC沿射线BC的方向平移2个单位后，得到 ‎ ⊿,连接，则⊿的周长是 12 .‎ 12. 如图，⊿ABC内接于⊙O ,AO=2 ,BC= ,则∠BAC的度数为 60 .‎ ‎ ‎ ‎ (第11题) (第12题) (第13题)‎ ‎13.如图，是将菱形ABCD以点O为中心按顺时针方向分别旋转90°,180°,270°后形成的图形，若 ∠BAD= 60°,AB=2 ,则图中阴影部分的面积为 12-4 .‎ ‎14.在Rt⊿ABC中，∠A=90°,有一个内角为60°，BC=6,若点P在直线AC上(不与点A、C重合)， ‎ ‎ 且∠ABP=30°,则CP的长为 2 , . 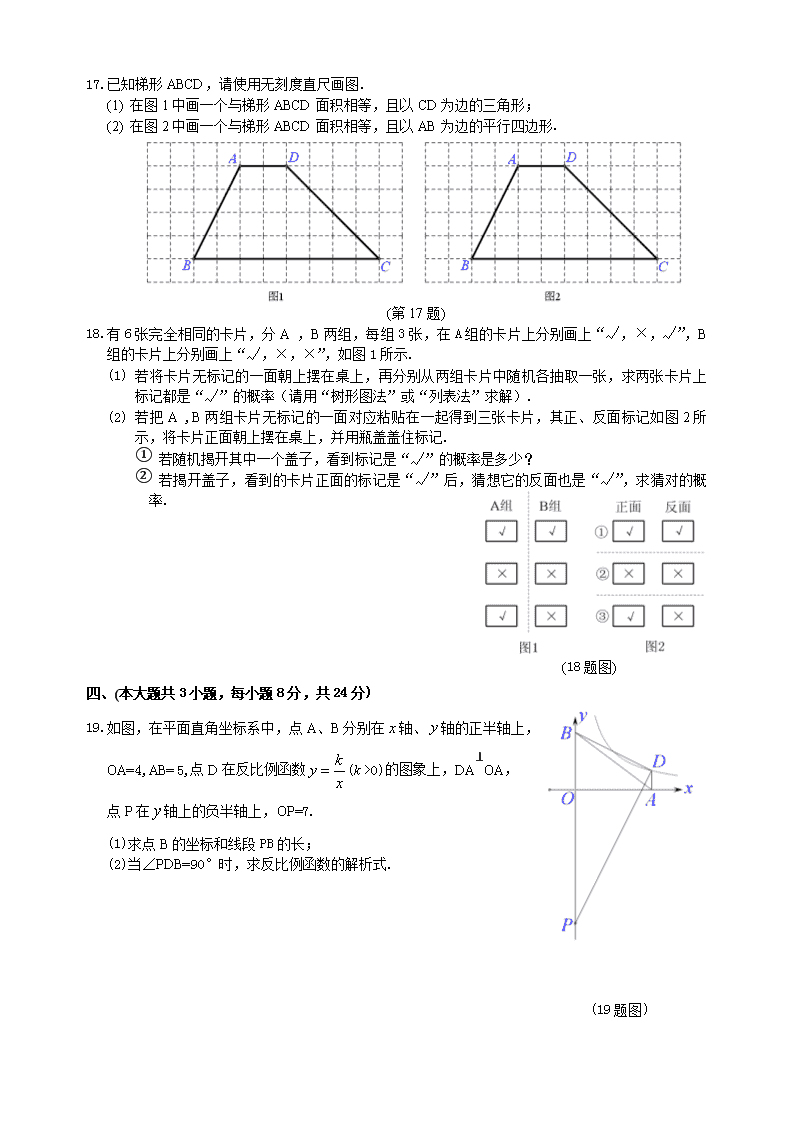‎ 三、(本大题共4小题，每小题6分，共24分)‎ ‎15.计算()‎ x-1‎ ‎16.小锦和小丽购买了价格分别相同的中性笔和笔芯.小锦购买了20支笔和2盒笔芯，用了56元；小 丽2支笔和3盒笔芯，仅用了28元，求每支中性笔和每盒笔芯的价格.‎ ‎2 8‎ ‎17.已知梯形ABCD，请使用无刻度直尺画图.‎ ‎ (1) 在图1中画一个与梯形ABCD面积相等，且以CD为边的三角形；‎ ‎ (2) 在图2中画一个与梯形ABCD面积相等，且以AB为边的平行四边形.‎ ‎ (第17题)‎ ‎18.有6张完全相同的卡片，分A ，B两组，每组3张，在A组的卡片上分别画上“√，×，√”，B 组的卡片上分别画上“√，×，×”，如图1所示.‎ ‎ (1) 若将卡片无标记的一面朝上摆在桌上，再分别从两组卡片中随机各抽取一张，求两张卡片上 标记都是“√”的概率（请用“树形图法”或“列表法”求解）.‎ ‎ (2) 若把A ,B两组卡片无标记的一面对应粘贴在一起得到三张卡片，其正、反面标记如图2所 示，将卡片正面朝上摆在桌上，并用瓶盖盖住标记.‎ ‎ ① 若随机揭开其中一个盖子，看到标记是“√”的概率是多少？‎ ‎ ② 若揭开盖子，看到的卡片正面的标记是“√”后，猜想它的反面也是“√”，求猜对的概 率.‎ ‎ (18题图)‎ 四、(本大题共3小题，每小题8分，共24分)‎ ‎19.如图，在平面直角坐标系中，点A、B分别在轴、轴的正半轴上，‎ ‎ OA=4,AB=5,点D在反比例函数(k >0)的图象上，DA⊥OA，‎ ‎ 点P在轴上的负半轴上，OP=7.‎ ‎ (1)求点B的坐标和线段PB的长；‎ ‎ (2)当∠PDB=90°时，求反比例函数的解析式.‎ ‎ ‎ ‎ (19题图)‎ ‎20.某教研机构为了解在校初中生阅读数学教科书的现状，随机抽取某校部分初中学生进行了调查， 依 据相关数据绘制成以下不完整的统计图，请根据图表中的信息解答下列问题：‎ ‎ 某校初中生阅读数学教科书情况统计图表 ‎ ‎ (1) 求样本容量及表格中、、的值，并补全统计图；‎ (2) 若该校共有初中生2300名，请估计该校“不重视阅读数学教科书”的初中生人数；‎ (3) ①根据上面的统计结果，谈谈你对该校初中生阅读数学教科书的现状的看法及建议；‎ ‎ ②如果要了解全省初中生阅读数学教科书的情况，你认为应该如何进行抽样？‎ 21. 图1中的中国结挂件是由四个相同的菱形在顶点处依次串接而成，每相邻两个菱形均成30°的夹 ‎ 角，示意图如图2所示，在图2中，每个菱形的边长为10㎝，锐角为60°.‎ ‎ (1)连接CD,EB,猜想他们的位置关系并加以证明；‎ ‎ (2)求A、B两点之间的距离(结果取整数，可以使用计算器）.‎ ‎ (参考数据: , ,)‎ ‎49‎ 五、(本大题共2小题，每小题9分，共18分)‎ ‎22.如图1，AB是⊙O的直径，点C在AB的延长线上，AB=4,BC=2，P是⊙O上半部分的一个动点， 连接OP,CP.‎ ‎ (1) 求⊿OPC的最大面积；‎ ‎ (2) 求∠OCP的最大度数；‎ ‎ (3) 如图2，延长PO交⊙O于点D,连接DB，当CP=DB时，求证：CP是⊙O的切线.‎ ‎ ‎ ‎ (第22题)‎ ‎23.如图1，边长为4的正方形ABCD中，点E在AB边上(不与点A，B重合),点F在BC边上(不与 点B，C重合).‎ ‎ 第一次操作：将线段EF绕点F顺时针旋转，当点E落在正方形上时，记为点G；‎ ‎ 第二次操作：将线段FG绕点G顺时针旋转，当点F落在正方形上时，记为点H；‎ ‎ 依此操作下去…‎ ‎ ‎ ‎ ‎ ‎ (第23题) ‎ ‎(1)图2中的⊿EFD是经过2次操作后得到的，其形状为 等边三角形 ，求此时线段EF的长；‎ ‎(2)若经过三次操作可得到四边形EFGH.‎ ‎ ①请判断四边形EFGH的形状为 ，此时AE与BF的数量关系是 ；‎ ‎ ②以①中的结论为前提，设AE的长为，四边形EFGH的面积为，求与的函数关系式 及面积的取值范围.‎ 六、 ‎(本大题共12分）‎ ‎24.如图1，抛物线 ()的顶点为,直线 与轴平行，且与抛物线交于 点A ,B,若⊿AMB为等腰直角三角形，我们把抛物线上A,B两点之间的部分与线段AB围成的图 形称为该抛物线对应的准碟形，线段AB称为碟宽，顶点称为碟顶，点到线段AB的距离称 为碟高.‎ ‎ (1)抛物线对应的碟宽为 2 ；抛物线对应的碟宽为 ；抛物线 ()对应的碟宽为 2 ；()对应的碟宽为 2 ；‎ ‎ (2)若抛物线(）对应的碟宽为6，且在轴上，求的值；‎ ‎ (3)将抛物线()的对应准碟形记为(=1,2,3…),定义 为相似准碟形，相应的碟宽之比即为相似比.若与的相似比为，且的碟顶是的 碟宽的中点，现将(2)中求得的抛物线记为 ，其对应的准碟形记为 .‎ ‎ ①求抛物线的表达式；‎ ‎ ②若的碟高为，若的碟高为，…，的碟高为 ，则 ，的碟 宽右端点横坐标为 ； 的碟宽的右端点是否在同一条直线上？若是， 直接写出该直线的表达式；若不是，请说明理由. ‎ ‎ (第24题图）‎