中考数学作图型试题复习 16页

作图型试题 一、网格问题 点阵中对称点、对称图形问题及利用格点进行面积计算已经成为最近几年中考试题的考点问题——考查学生平移变换，利用勾股定理进行三角形的有关计算，全等及相似三角形的判定。‎ 例1、已知图1和图2中的每个小正方形的边长都是1个单位.‎ ‎（1）将图1中的格点△ABC，先向右平移3个单位，再向上平移2个单位，得到△A1B1C1，请你在图1中画出△A1B1C1.‎ ‎（2）在图2中画出一个与格点△DEF相似但相似比不等于1的格点三角形.‎ 图2‎ F D E A B C 图1‎ 分析：本题关键是计算出△ABC的三边的长度，然后找一个不等于1的相似比，比如相似比为2，计算出△DEF三边长或计算出一边长后，利用平移得出△DEF。‎ 图2‎ F D E A B C 图1‎ A1‎ B1‎ C1‎ 答案：（1） （2）答案不唯一.‎ ‎ ‎ 练习一 图1‎ ‎1、在4×4的正方形网格中，每个小方形的边长都是1。线段AB和CD分别是（图1）中1×3的两个矩形的对角线，显然AB∥CD。请你用类似的方法画出过点E且垂直于AB的直线，并证明。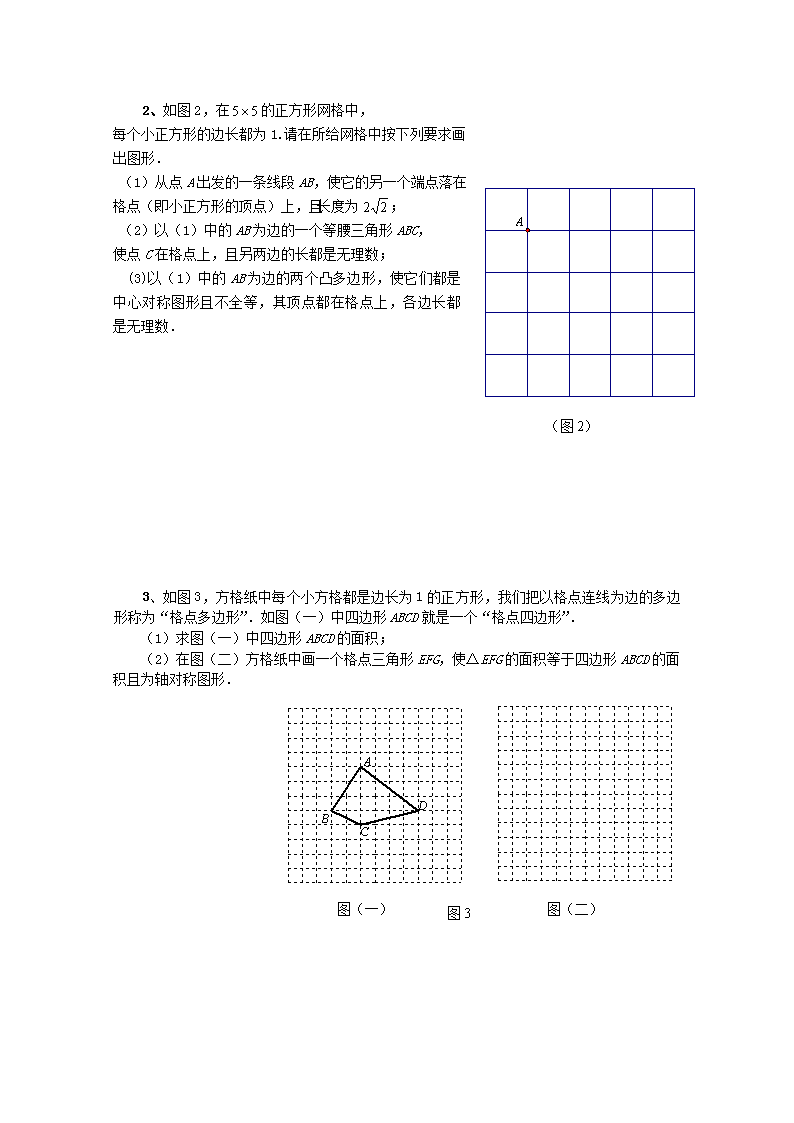‎ ‎2、如图2，在的正方形网格中，‎ 每个小正方形的边长都为1.请在所给网格中按下列要求画 出图形．‎ ‎（图2）‎ ‎（1）从点A出发的一条线段AB，使它的另一个端点落在格点（即小正方形的顶点）上，且长度为；‎ ‎（2）以（1）中的AB为边的一个等腰三角形ABC，‎ 使点C在格点上，且另两边的长都是无理数；‎ ‎(3)以（1）中的AB为边的两个凸多边形，使它们都是中心对称图形且不全等，其顶点都在格点上，各边长都是无理数．‎ ‎3、如图3，方格纸中每个小方格都是边长为1的正方形，我们把以格点连线为边的多边形称为“格点多边形”．如图（一）中四边形ABCD就是一个“格点四边形”．‎ ‎（1）求图（一）中四边形ABCD的面积；‎ 图3‎ ‎（2）在图（二）方格纸中画一个格点三角形EFG，使△EFG的面积等于四边形ABCD的面积且为轴对称图形．‎ ‎ ‎ ‎ 　　　　　　　　 　　图（一）　　　　　　　　　　　图（二）‎ A B C O 图4‎ ‎4、如图，是格点（横、纵坐标都为整数的点）三角形，请在图中画出与全等的一个格点三角形．‎ ‎5、已知：如图，□ABCD.‎ ‎(1)画出□A1B1C1D1使□A1B1C1D1与□ABCD关于直线MN对称;‎ ‎(2)画出□A2B2C2D2,使□A2B2C2D2与□ABCD关于点O中心对称;‎ ‎(3) □A1B1C1D1与□A2B2C2D2是对称图形吗?若是,请在图上画出对称轴或对称中心 A B C D M O 图5‎ 二、图形分割 对于图形分割，是历年来各省市的中考试题的一个考点也是难点之一。它要求学生除了考查学生的基础知识（如图形的面积计算）外，还能较好的考查学生的观察、分析、创新能力。‎ 例2、（2005年河南课改）有一块梯形状的土地，现要平均分给两个农户种植(即将梯形的面积两等分)，试设计两种方案(平分方案画在备用图上)，并给予合理的解释。‎ 分析：一般对于简单的图形可直观的进行分割，而对于稍复杂的题目，是通过计算或是转化为三角形问题来解决的。‎ 解：设梯形上、下底分别为a、b，高为h。‎ 方案一：如图1，连结梯形上、下底的中点E、F，则S四边形ABFE＝S四边形EFCD＝ 方案二：如图2，分别量出梯形上、下底a、b的长，在下底BC上截取BE＝(a＋b)，连接AE，则S△ABE＝S四边形AECD＝。‎ 方案三：如图3，连结AC，取AC的中点E，连结BE、ED，则图中阴影部分的面积等于梯形ABCD的面积的一半。‎ 分析此方案可知，∵AE＝EC，∴S△AEB＝S△EBC，S△AED＝S△ECD，‎ ‎∴S△AEB＋S△AED＝S△EBC＋S△ECD，‎ ‎∴图中阴影部分的面积等于梯形ABCD的面积的一半 练习二 图1‎ ‎1.在一次数学实践探究活动中，小强用两条直线把平行四边形ABCD分割成四个部分，使含有一组对顶角的两个图形全等；‎ ‎（1）根据小强的分割方法，你认为把平行四边形分割成满足以上全等关系的直线 有 组；‎ ‎（2）请在图1的三个平行四边形中画出满足小强分割方法的直线；‎ ‎（3）由上述实验操作过程，你发现所画的饿两条直线有什么规律？‎ ‎2.如图2，RtΔABC中，∠ACB=90°，∠CAB=30°，用圆规和直尺作图，用两种方法把它分成两个三角形，且要求其中一个三角形的等腰三角形。（保留作图痕迹，不要求写作法和证明）‎ 图2‎ ‎3.蓝天希望学校正准备建一个多媒体教室，计划做长120cm，宽30cm的长条形桌面。现只有长80cm，宽45cm的木板，请你为该校设计不同的拼接方案，使拼出来的桌面符合要求。（只要求画出裁剪、拼接图形，并标上尺寸，设计出一种得5分，设计出两种再加1分）‎ ‎80cm ‎45cm ‎80cm ‎45cm ‎4. 小芸在为班级办黑板报时遇到了一个难题，在版面设计过程中需将一个半圆面三等分，请你帮助她设计一个合理的等分方案．要求用尺规作出图形，保留作图痕迹，并简要写出作法．‎ ‎5.　学校有一块如图所示的扇形空地，请你把它平均分成两部分．‎ ‎（要求：用尺规作图，保留作图痕迹，写出作法，不用证明．）‎ 三、能力提高 ‎1.如图，有一木制圆形脸谱工艺品，、两点为脸谱的耳朵，打算在工艺品反面两耳连线中点处打一小孔．现在只有一块无刻度单位的直角三角板（斜边大于工艺品的直径），请你用两种不同的方法确定点的位置（画出图形表示），并且分别说明理由．‎ ‎2、．用四块如图1所示的瓷砖拼成一个正方形图案，使拼成的图案成一个轴对称图形（如图2），请你分别在图3、图4中各画一种与图2不同的拼法，要求两种拼法各不相同，且其中至少有一个图形既是中心对称图形，又是轴对称图形。‎ 图1‎ 图2‎ 图3‎ 图4‎ A　　　　　　　　　　B D　　　　　　　　　　‎ ‎　　　　　　　‎ C ‎3如图，己知四边形ABCD，用尺规将它放大，使放大前后的图形对应线段的比为1：2.(不写作法，但保留作图痕迹) ‎ ‎　　‎ ‎4.某新建小区要在一块等边三角形的公共区域内修建一个圆形花坛。‎ ‎ （1）若要使花坛面积最大，请你在这块公共区域（如图）内确定圆形花坛的圆心P；‎ ‎ （2）若这个等边三角形的边长为18米，请计算出花坛的面积。‎ ‎5．‎ ‎（1）在图3所示编号为①、②、③、④的四个三角形中，关于y轴对称的两个三角形的编号为　　　　　　　　；关于坐标原点O对称的两个三角形的编号为　　　　　　　　；‎ ‎（2）在图4中，画出与△ABC关于x轴对称的△A1B1C1‎ ‎6．如图，平行四边形纸条ABCD中，E、F分别是边AD、BC的中点。张老师请同学们将纸条的下半部分平行四边形ABEF沿EF翻折，得到一个V字形图案。‎ ‎(1)请你在原图中画出翻折后的图形平行四边形A1B1FE；‎ ‎(用尺规作图，不写画法，保留作图痕迹)‎ ‎(2)已知∠A=63°，求∠B1FC的大小。‎ ‎7．小明家用瓷砖装修卫生间，还有一块墙角面未完工(如图甲所示)，他想在现有的六块瓷砖余料中(如图乙所示)挑选2块或3块余料进行铺设，请你帮小明设计两种不同的铺设方案(在下面图丙、图丁中画出铺设示意图，并标出所选用每块余料的编号)。‎ ‎8.已知：如图，现有的正方形和的矫形纸片若干块，试选用这些纸片（每种至少用一次）在下面的虚线方框中拼成一个矫形（每两个纸片之间既不重叠，也无空隙，批出的图中必须保留拼图的痕迹），使批出的矫形面积为，并标出此矫形的长和宽。‎ ‎9.一条小船，‎ （1） 若把小船平移，使点A平移到点B，请你在图中画出平移后的小船；‎ （2） 若该小船先从点A航行到达岸边L的点P处补给后，再航行到点B，但要求航程最短 ‎，试在图中画出点P的位置。‎ ‎10.某公园有一个边长为4米的正三角形花坛，三角形的顶点A、B、C上各有一棵古树．现决定把原来的花坛扩建成一个圆形或平行四边形花坛，要求三棵古树不能移动，且三棵古树位于圆周上或平行四边形的顶点上．以下设计过程中画图工具不限．‎ ‎（1）按圆形设计，利用图1画出你所设计的圆形花坛示意图；‎ ‎（2）按平行四边形设计，利用图2画出你所设计的平行四边形花坛示意图；‎ 图1‎ 图2‎ A B C A B C ‎（3）若想新建的花坛面积较大，选择以上哪一种方案合适？请说明理由 ‎ ‎ ‎11. 在下面方格纸中设计一个对称图案，在这个图案中必须用到等腰三角形、正方形、圆三种基本图形。‎ ‎12、下面是天都市三个旅游景点的平面图，请你选用适当的方式借助刻度尺、量角器等基本作图工具，确定出三个景点的位置。‎ 天都市旅游景点示意图 碑林 博物馆 动物园 北 比例尺 ‎0‎ ‎5‎ ‎10千米 ‎13、平移方格纸中的图形（如图），使A点平移到A′点处，画出平移后的图形，并写上一句贴切、诙谐的解说词．‎ A ·‎ ‎·A′‎ 解说词： ‎ 四、参考答案 练习一 ‎1.‎ ‎（第2题答图1）‎ ‎（第2题答图2）‎ ‎2.‎ ‎3. （1）方法一：S＝‎ ‎×6×4＝12 ‎ 方法二：S＝4×6－×2×1－×4×1－×3×4－×2×3＝12‎ ‎　 （2）（只要画出一种即可）‎ ‎4. 只画出一个符合题意的三角形即可.‎ ‎5. (1)如图，平行四边形A1B1C1D1，就是所求的平行四边形. -‎ ‎(2)如图，平行四边形A2B2C2D2，就是所求的平行四边形.‎ ‎(3)是轴对称图形，对称轴是直线EF. ‎ 练习二 ‎1.（1）无数；‎ ‎（2）只要两条直线都过对角线的交点就给满分；‎ ‎（3）这两条直线过平行四边形的对称中心（或对角线的交点）；‎ ‎2. 解：作法一：作AB边上的中线；‎ ‎ 作法二：作∠CBA的平分线；‎ ‎ 作法三：在CA上取一点D，使CD=CB。‎ ‎ ‎ ‎3.‎ ‎4.　 作法：‎ ‎(1)作AB的垂直平分线CD交AB于点O；‎ ‎(2)分别以A、B为圆心，以AO(或BO)的长为半径画弧，分别交半圆干点M、N；(3)连结OM、ON即可．‎ ‎5.　 解法一：‎ ‎（1）以O为圆心，任意长为半径画弧，分别交OA、OB于C、D两点；‎ ‎（2）分别以C、D为圆心，大于的长为半径画弧，两弧交于E点（不与O点重合）；‎ 注：也可直接以A、B为圆心作图． ‎ ‎（3）射线OE交弧AB于F； ‎ 则线段OF将扇形AOB二等分。 ‎ 解法二：1）连接AB；‎ ‎2）分别以A、B为圆心，大于的长为半径画弧，两弧交于C点（不与O点重合）；‎ ‎3）连接OC交弧AB于D点；则线段OD将扇形AOB二等分．‎ 能力提高 ‎1． ‎ 方法一：如图①，画TH的垂线L交TH于D，则点D就是TH的中点。‎ 依据是垂径定理。 ‎ 方法二：如图②，分别过点T、H画HC⊥TO，TE⊥HO，HC与TE相交于点F，过点O、F画直线 L交HT于点D，则点D就是HT的中点。‎ 由画图知，Rt△HOC≌Rt△TOE，易得HF=TF，又OH=OT 所以点O、F在HT的中垂线上，所以HD=TD ‎ 方法三：如图③，（原理同方法二） ‎ ‎2、‎ ‎3D D1‎ C C1‎ B1‎ B A D1‎ D C1‎ C B1‎ B A .可按位似图形放大，且位似中心的位置可在图形顶点处、图形边上、图形内部、图形外部，在每一处都会有两种图形，因此，此题属开放试题，仅举示例供参考：‎ ‎　　‎ ‎4.(1)‎ ‎（2）‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎5.(1) ①、②； ①、③.‎ ‎(2)如图 ‎6. 1）作图如图；‎ ‎ （2）‎ ‎7. 列举以下四种铺设的示意图供参考 ‎8. 答案不唯一。‎ ‎9. （1）平移后的小船如图所示…………5分 ‎（2）如图，点A’与点A关于直线L成轴对称，连接A’B交直线L于点P，则点P为所求。‎ ‎10. （1）作图工具不限，只要点A、B、C在同一圆上；‎ ‎ （2）作图工具不限，只要点A、B、C在同一平行四边形顶点上；‎ ‎ （3）∵r=OB==，‎ ‎ ∴S⊙O=r2=≈16.75， ‎ ‎ 又S平行四边形=2S△ABC=2××42×sin60º=8≈13.86,‎ ‎ ∵S⊙O > S平行四边形 ∴选择建圆形花坛面积较 ‎11. 略 ‎10千米 ‎30°‎ ‎30°‎ ‎60°‎ ‎60°‎ ‎45°‎ ‎45°‎ 碑林 ‎4cm ‎6cm ‎2cm 参 考 图 天都市旅游景点示意图 ‎ ‎ ‎ ‎ ‎ ‎ 博物馆 动物园 北 比例尺 ‎0‎ ‎5‎ 参 考 图 ‎10千米 碑林 ‎60°‎ ‎45°‎ ‎2cm 天都市旅游景点示意图 ‎ ‎ ‎ ‎ 博物馆 动物园 北 比例尺 ‎0‎ ‎5‎ ‎4cm ‎12.‎