河南省郑州市八中中考模拟数学试题及答案 6页

班级： 姓名： 考号： ‎ ‎2014年河南省郑州市八中 中考模拟数学试题 ‎ 满分：100分 考试时间：120分钟 2014.4‎ 友情提示：亲爱的同学，请你保持轻松的心态，认真审题，仔细作答，发挥自己正常的水平，相信你一定行。预祝你取得满意的成绩！‎ 题号 一 二 三 总分 ‎16‎ ‎17‎ ‎18‎ ‎19‎ ‎20‎ ‎21‎ ‎22‎ ‎23‎ 得分 一．选择题(下列各题的四个选项中，只有一项符合题意，每小题3分，共30分) ‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 选项 ‎1. 代数式中x的取值范围是（　　）‎ ‎　 A．x≥－　　 B． x≥　　　 C．　 x＞　　　　 D． x＞－ ‎ ‎2．在下列图形中，即是轴对称图形，又是中心对称图形的是（ ）‎ A． B． C． D．‎ ‎2‎ A ‎－1‎ ‎0‎ ‎1‎ ‎3．如图，以数轴的单位长线段为边作一个正方形，以数轴的原点为旋转中心，将过原点的对角线顺时针旋转，使对角线的另一端点落在数轴正半轴的点A处，则点A表示的数是（ ）‎ A. B. 1.4 C. D. ‎ ‎4．甲、乙、丙、丁四人进行射击测试，每人10次射击成绩的平均数均是9.2环，方差分别为，，，，则成绩最稳定的是（ ）‎ A．甲 B．乙 C．丙 D．丁 ‎5．如图，是小明用八块小正方体搭的积木，该几何体的俯视图是 ( )．‎ ‎6.已知抛物线与轴的一个交点为，则代数式的值为（ ）‎ A．2014 B．2013 C．2012 D．2011‎ ‎7．在一个可以改变容积的密闭容器内，装有一定质量m的某种气体，当改变容积V时，气体的密度也随之改变．与V在一定范围内满足，它的图象如图2所示，则该气体的质量m为( )‎ A．1.4kg B．5kg C．7kg. D．0.28kg ‎8．点A、B、C在一次函数的图象上，它们的横坐标依次为-1、1、2，分别过这些点作x轴与y轴的垂线，则图中阴影部分的面积这和是 （ ）‎ A． B． C． D．‎ V（m3） ‎ ‎（kg/ m3）‎ O ‎（5, 1.4）‎ ‎1.4‎ ‎5‎ ‎ ‎ 第7题图 第8题图 第9题图 ‎9.一个滑轮起重装置，如图4所示，滑轮的半径是10cm，当重物上升10cm时，滑轮的一条半径OA，绕轴心O按逆时针方向旋转的角度约为（假定设绳索与滑轮之间没有滑动，∏取3.14，结果精确到10）（ ）‎ A. 1150 B. 600 C. 570 D. 290‎ ‎10.为了求的值，可令S＝，则2S＝ ，因此2S-S＝，所以＝仿照以上推理计算出的值是（ ）‎ A. B. C. 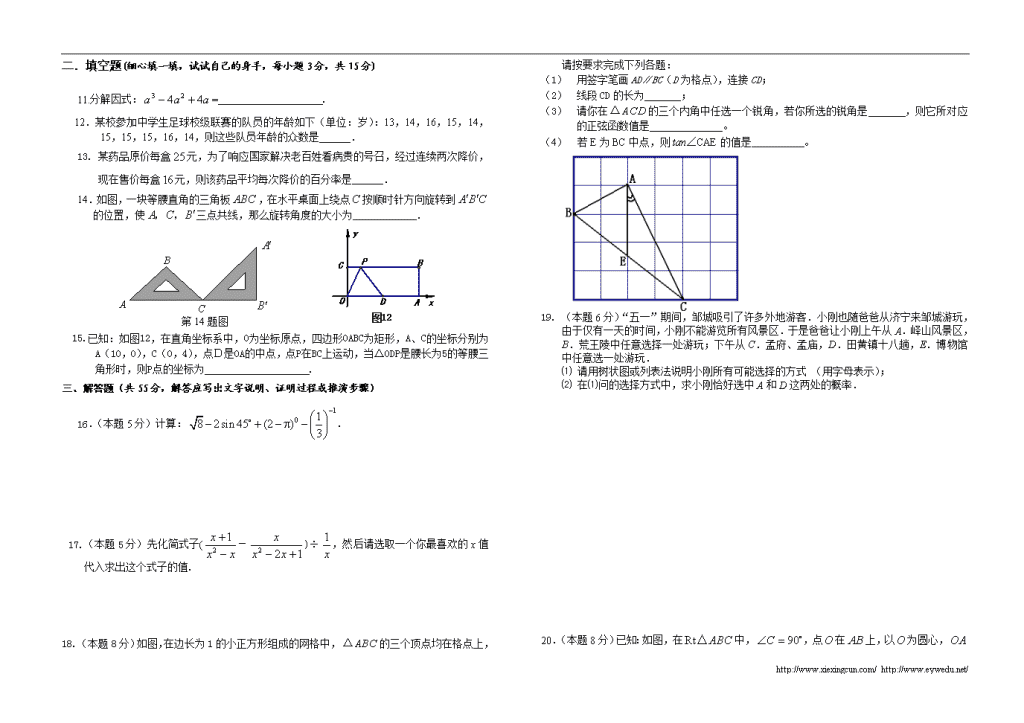D.‎ http://www.xiexingcun.com/ http://www.eywedu.net/‎ 二．填空题(细心填一填，试试自己的身手，每小题3分，共15分)‎ ‎11.分解因式：= . ‎ ‎12．某校参加中学生足球校级联赛的队员的年龄如下（单位：岁）：13，14，16，15，14，15，15，15，16，14，则这些队员年龄的众数是______．‎ ‎13. 某药品原价每盒元，为了响应国家解决老百姓看病贵的号召，经过连续两次降价，现在售价每盒元，则该药品平均每次降价的百分率是______． ‎ ‎14．如图，一块等腰直角的三角板，在水平桌面上绕点按顺时针方向旋转到 的位置，使三点共线，那么旋转角度的大小为 ．‎ B A C 第14题图 ‎ ‎图12‎ ‎15.已知：如图12，在直角坐标系中，O为坐标原点，四边形OABC为矩形，A、C的坐标分别为A（10，0），C（0，4），点Ｄ是OA的中点，点P在BC上运动，当△ODP是腰长为5的等腰三角形时，则P点的坐标为 .‎ 三、解答题（共55分，解答应写出文字说明、证明过程或推演步骤）‎ ‎16．（本题5分）计算：．‎ ‎17.（本题5分）先化简式子(－)÷，然后请选取一个你最喜欢的x值代入求出这个式子的值.‎ ‎18. （本题8分）如图，在边长为1的小正方形组成的网格中，的三个顶点均在格点上，请按要求完成下列各题：‎ （1） 用签字笔画AD∥BC（D为格点），连接CD；‎ （2） 线段CD的长为 ；‎ （3） 请你在的三个内角中任选一个锐角，若你所选的锐角是 ，则它所对应的正弦函数值是 。‎ ‎（4） 若E为BC中点，则tan∠CAE的值是 。‎ ‎19. （本题6分）“五一”期间，邹城吸引了许多外地游客．小刚也随爸爸从济宁来邹城游玩，由于仅有一天的时间，小刚不能游览所有风景区．于是爸爸让小刚上午从A．峄山风景区，B．荒王陵中任意选择一处游玩；下午从C．孟府、孟庙，D．田黄镇十八趟，E．博物馆中任意选一处游玩．‎ ‎⑴ 请用树状图或列表法说明小刚所有可能选择的方式 （用字母表示）；‎ ‎⑵ 在⑴问的选择方式中，求小刚恰好选中A和D这两处的概率．‎ ‎20．（本题8分）已知：如图，在中，，点在上，以为圆心，‎ http://www.xiexingcun.com/ http://www.eywedu.net/‎ 长为半径的圆与分别交于点，且．‎ ‎（1）判断直线与⊙的位置关系，并证明你的结论；‎ D C O A B E ‎（2）证明：‎ ‎（3）若DC=3，BC=4，求AB的长度。 ‎ ‎ ‎ ‎21.（本题8分）我市香城镇培育了一种可食用菌，上市时，李经理按市场价格30元/千克收购了这种食用菌1000千克存放入冷库中，据预测，该食用菌的市场价格将以每天每千克上涨1元；但冷冻存放这批食用菌时每天需要支出各种费用合计310元，而且这类食用菌在冷库中最多保存160天，同时，平均每天有3千克的食用菌损坏不能出售．‎ ‎（1）设天后每千克该食用菌的市场价格为元，试写出与之间的函数关系式．‎ ‎（2）若存放天后，将这批食用菌一次性出售，设这批食用菌的销售总额为元，试写出与之间的函数关系式．‎ ‎（3）李经理将这批食用茵存放多少天后出售可获得最大利润元？‎ ‎（利润＝销售总额－收购成本－各种费用）‎ ‎22. （本题7分）如图，在正方形ABCD中，E是AB边上任意一点，BG⊥‎ http://www.xiexingcun.com/ http://www.eywedu.net/‎ CE，垂足为点O,交AC于点F，交AD于点G。‎ E B A O F G C D 第22题图 （1） 证明：BE=AG ；‎ （2） 点E位于什么位置时，∠AEF=∠CEB，说明理由。‎ ‎23．(本题8分)设抛物线与x轴交于两个不同的点A(1，0)、B(m，0)，对称轴为直线x=－1，顶点记为点C.且∠ACB=90°．‎ ‎(1)求m的值和抛物线的解析式；‎ ‎(2)已知过点A的直线交抛物线于另一点E．若点P在x轴上，以点P、B、C为顶点的三角形与△AEB相似，求点P的坐标．‎ ‎(3)在(2)的条件下，△BCP的外接圆半径等于________________．（直接写答案）‎ A O B E C x y http://www.xiexingcun.com/ http://www.eywedu.net/‎ 数学试题参考答案及评分意见 一、 选择题（下列各题的四个选项中，只有一项符合题意，每小题3分，共30分。）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 A C D D D A C ‎ B C D 二、填空题：（每小题3分，共15分）‎ ‎11. 12. 15 13. 20% ‎ ‎14. 15. P（3，4）P（2，4）P（8，4） ‎ 三、解答题（共55分，解答应写出文字说明、证明过程或推演步骤）‎ ‎16.（本题5分）解：‎ ‎=……………………………………………3分 ‎．………………………………………………………5分 ‎17．（本题5分）原式=，…………3分 代值（注：所代值不能为0，1）（略）…………5分 第18题图 ‎18.（本题8分）‎ ‎（1）如图…………………………………2分 ‎（2）…………………………………4分 ‎（3）∠CAD，(或∠ADC，)……………6分 开始 第一天 第二天 A D C E B D C E ‎（4）……………8分 ‎19.(本题6分）‎ ‎（1）解法一：‎ 所有可能出现的结果（A，C）（A，D）（A，E）（B，C）（B，D）（B，E）‎ ‎∴小刚所有可能选择的方式有6种． 3分 解法二：‎ 第二天 第一天 C D E A ‎（A，C）‎ ‎（A，D）‎ ‎（A，E）‎ B ‎（B，C）‎ ‎（B，D）‎ ‎（B，E）‎ ‎∴小刚所有可能选择的方式有6种． 3分 ‎（2）∵一共有六种等可能的结果，而恰好选中A、D两处的可能性只有一种，‎ ‎∴小刚恰好选中A和D这两处的概率为． ……………………6分 ‎20．（本题8分）解：（1）直线与⊙相切．‎ 证明：如图1，连结．‎ ‎，‎ ‎．‎ D C O A B E 图1‎ ‎， ．‎ 又，‎ ‎．‎ ‎．‎ 直线与⊙相切． ………………………………………… 3分 ‎（2）∵为公共角，‎ ‎∴△CBD∽△CAB ‎∴‎ ‎∴ ………………………………………… 5分 ‎（3）法1：△BCD中,由勾股定理得BD=5‎ ‎ 由△CBD∽△CAB ‎∴‎ ‎∴AB= ………………………………………… 8分 法2：：由（2）易求AC，在直角△ABC中用勾股定理求AB。‎ ‎21．（本题8分）‎ ‎①由题意得与之间的函数关系式（，且整数） 2分 http://www.xiexingcun.com/ http://www.eywedu.net/‎ ‎（不写取值范围不扣分）‎ ‎②由题意得与之间的函数关系式：‎ ‎ 5分 ‎③由题意得 ‎ 7分 ‎∴当时， ‎ ‎∴存放100天后出售这批食用菌可获得最大利润30000元． 8分 ‎（用抛物线的顶点坐标公式求最值可参照给分）‎ ‎22. （本题7分）（1）证明：∵四边形ABCD是正方形 ‎∴∠ABC=∠BAD=90°，∴∠1+∠3=90°，‎ ‎∵BG⊥CE,∴∠BOC=90°∴∠2+∠3=90°,‎ ‎∴∠1=∠2 ………………………2分 在△GAB和△EBC中，‎ ‎∵∠GAB=∠EBC=90°,AB=BC,∠1=∠2‎ ‎∴△GAB≌△EBC (ASA) ‎ ‎∴AG=BE ………………………… 3分 ‎1‎ E B A O F G C D 第22题图 ‎3‎ ‎2‎ ‎（2）解：当点E位于线段AB中点时，∠AEF=∠CEB …… 4分 理由如下：若当点E位于线段AB中点时，则AE=BE,‎ 由（1）可知，AG=BE ∴AG=AE ‎∵四边形ABCD是正方形，∴∠GAF=∠EAF=45°‎ 又∵AF=AF,∴△GAF≌△EAF (SAS)‎ ‎∴∠AGF=∠AEF ………………………………………6分 由（1）知，△GAB≌△EBC ∴∠AGF=∠CEB,‎ ‎∴∠AEF=∠CEB ………………………………… 7分 ‎23．（1）（1分）‎ 对称轴求a和点B坐标，点A代人求C, （2分）‎ ‎（2）△BCP∽△AEB时得 ‎ 或 △BCP∽△ABE时得 （每种情况讨论各得2分）‎ ‎(3)或（每个答案各1分）‎ http://www.xiexingcun.com/ http://www.eywedu.net/‎