4月上海市虹口区中考数学二模卷 6页

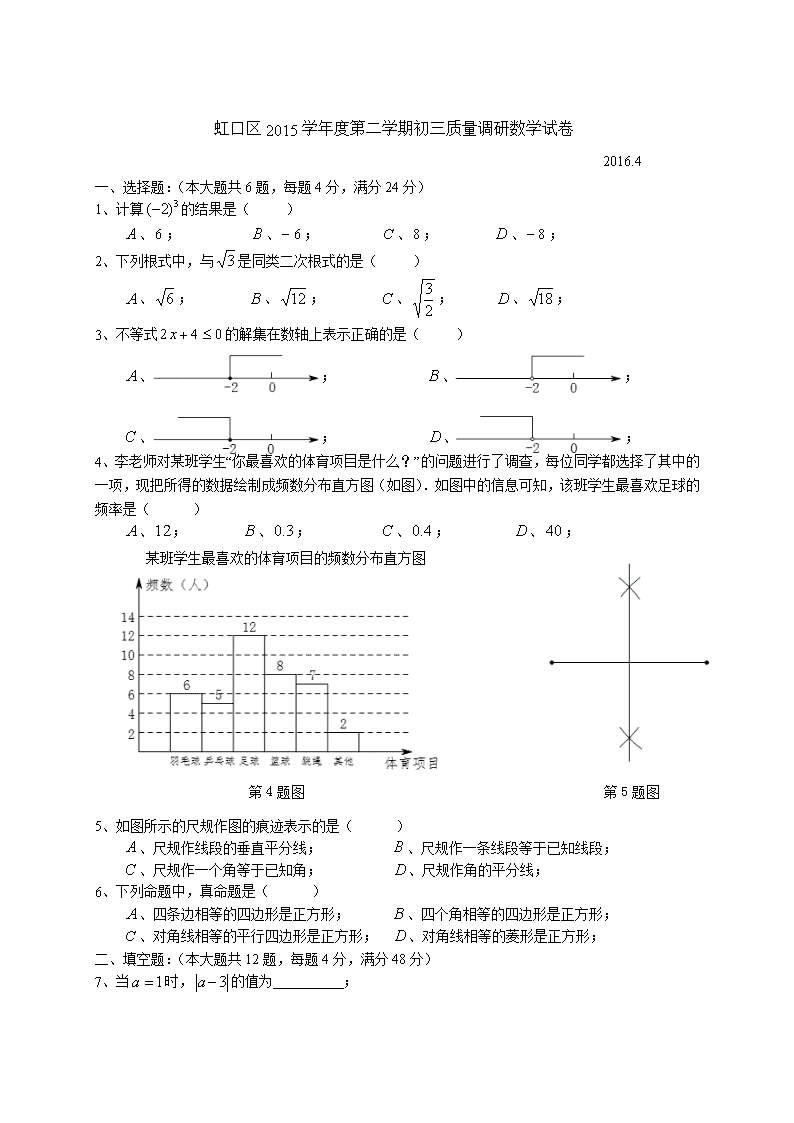
‎ 虹口区2015学年度第二学期初三质量调研数学试卷 ‎ 2016.4‎ 一、选择题：（本大题共6题，每题4分，满分24分）‎ ‎1、计算的结果是（ ）‎ ‎ 、； 、； 、； 、；‎ ‎2、下列根式中，与是同类二次根式的是（ ）‎ ‎ 、； 、； 、； 、；‎ ‎3、不等式的解集在数轴上表示正确的是（ ）‎ ‎ 、 ； 、 ； ‎ ‎ 、 ； 、 ；‎ ‎4、李老师对某班学生“你最喜欢的体育项目是什么？”的问题进行了调查，每位同学都选择了其中的一项，现把所得的数据绘制成频数分布直方图（如图）．如图中的信息可知，该班学生最喜欢足球的频率是（ ）‎ 某班学生最喜欢的体育项目的频数分布直方图 第4题图 ‎ 、； 、； 、； 、；‎ 第5题图 ‎5、如图所示的尺规作图的痕迹表示的是（ ）‎ ‎ 、尺规作线段的垂直平分线； 、尺规作一条线段等于已知线段； ‎ ‎ 、尺规作一个角等于已知角； 、尺规作角的平分线；‎ ‎6、下列命题中，真命题是（ ）‎ ‎ 、四条边相等的四边形是正方形； 、四个角相等的四边形是正方形； ‎ ‎ 、对角线相等的平行四边形是正方形； 、对角线相等的菱形是正方形；‎ 二、填空题：（本大题共12题，每题4分，满分48分）‎ ‎7、当时，的值为 ；‎ ‎8、方程的根是 ；‎ ‎9、若关于的方程有两个不相等的实数根，则的取值范围是 ；‎ ‎10、试写出一个二元二次方程，使该方程有一个解是，你写的这个方程是 （写出一个符合条件的即可）；‎ ‎11、函数的定义域是 ；‎ ‎12、若、是二次函数图像上的两点，则 （填“”或“”或“”）；‎ ‎13、一个不透明纸箱中装有形状、大小、质地等完全相同的7个小球，分别标有数字1、2、3、4、5、6、7，从中任意摸出一个小球，这个小球上的数字是奇数的概率是 ；‎ ‎14、已知某班学生理化实验操作测试成绩的统计结果如下表：‎ 成绩（分）‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 人数 ‎1‎ ‎2‎ ‎2‎ ‎6‎ ‎9‎ ‎11‎ ‎9‎ ‎ ‎ ‎ 则这些学生成绩的众数是 分；‎ 第18题图 第15题图 ‎15、如图，在梯形中，、分别为腰、的中点，若，，则向量 （结果用表示）；‎ ‎16、若两圆的半径分别为和，圆心距为，则这两圆的位置关系是 ；‎ ‎17、设正边形的半径为，边心距为，如果我们将的值称为正边形的“接近度”，那么正六边形的“接近度”是 （结果保留根号）；‎ ‎18、已知中，，（如图所示），将沿射线方向平移个单位得到，顶点、、分别与、、对应，若以点、、为顶点的三角形是等腰三角形，且为腰，则的值是 ；‎ 三、解答题：（本大题共7题，满分78分）‎ ‎19、（本题满分10分）先化简，再求值：，其中；‎ ‎20、（本题满分10分，第（1）小题满分6分，第（2）小题满分4分）‎ 已知一个二次函数的图像经过、、三点．‎ ‎（1）求这个二次函数的解析式；‎ ‎（2）用配方法把这个函数的解析式化为的形式；‎ ‎21、（本题满分10分）‎ 第21题图 如图，在中，是边上的中线，是锐角，且，，，求边的长和的值；‎ ‎22、（本题满分10分）‎ 社区敬老院需要600个环保包装盒，原计划由初三（1）班全体同学制作完成。但在实际制作时，有10名同学因为参加学校跳绳比赛而没有参加制作．这样，该班实际参加制作的同学人均制作的数量比原计划多5个，那么这个班级共有多少名同学？‎ ‎23、（本题满分12分，第（1）小题满分6分，第（2）小题满分6分）‎ 如图，在四边形中，∥，、为对角线上两点，且，∥．‎ ‎（1）求证：四边形是平行四边形；‎ ‎（2）延长，交边于点，交边的延长线于点，求证：．‎ 第23题图 ‎24、（本题满分14分，其中第（1）小题满分4分，第（2）小题满分4分，第（3）小题满分4分）‎ 如图，在平面直角坐标系中，直线过点、（），；‎ ‎（1）求直线的表达式；‎ ‎（2）反比例函数的图像与直线交于第一象限内的、两点（），当时，求的值；‎ ‎（3）设线段的中点为，过点作轴的垂线，垂足为点，交反比例函数的图像于点，分别联结、，当∽时，请直接写出满足条件的所有的值；‎ 第24题图 ‎25、（本题满分14分，其中第（1）小题满分4分，第（2）小题满分5分，第（3）小题满分5分）‎ 如图，在中，，．点、分别在边、上，，以为半径的⊙交的延长线于点．‎ ‎（1）当为边中点时（如图1），求弦的长；‎ ‎（2）设，，求关于的函数解析式及定义域；（不用写出定义域）；‎ 图2‎ 第25题图 ‎（3）若过的重心，分别联结、、，当时（如图2），求的值；‎ 图1‎