2008年湖北省宜昌市初中毕业生学业考试卷及参考答案 16页

‎2008年湖北省宜昌市初中毕业生学业考试 数 学 试 卷 ‎（考试形式：闭卷 全卷共四大题25小题 卷面满分：120分 考试时限：120分钟）‎ 考生注意：‎ ‎1．本试卷分为两卷，解答第I卷(1～2页)时请将解答结果填写在第II卷(3～8页)上指定的位置，否则答案无效，交卷时只交第II卷．‎ ‎2．答卷时允许使用科学计算器．‎ ‎3．以下数据、公式供参考：sin47°≈0.731，cos47°≈0.682；二次函数y＝ax2＋bx＋c图象的顶点坐标是；＝（R为半径, l为弧长）．‎ 第Ⅰ卷（选择题、填空题 共45分）‎ 一、选择题：（在各小题给出的四个选项中，只有一项是符合题目要求的，请将符合要求的选项前面的字母代号填写在第II卷上指定的位置. 本大题共10小题，每题3分，计30分）‎ ‎1．下列物体的形状类似于球的是（ ）．‎ A．茶杯 B．羽毛球 C．乒乓球 D．白炽灯泡 ‎2．若火箭发射点火前5秒记为－5秒，那么火箭发射点火后10秒应记为（ ）．‎ A．－10秒 B．－5秒 C．＋5秒 D．＋10秒 ‎(第3题)‎ ‎3．如图是江峡中学实验室某器材的主视图和俯视图，‎ 那么这个器材可能是（ ）．‎ A．条形磁铁 B．天平砝码 ‎ C．漏斗 D．试管 ‎4．从实数－，－ ，0，π，4中，挑选出的两个数都是无理数的为（ ）．‎ A．－ ，0 B．π，‎4 C．－，4 D．－，π ‎5．若气象部门预报明天下雨的概率是80%，下列说法正确的是（ ）．‎ A．明天一定会下雨 B．明天一定不会下雨 ‎(第6题)‎ C．明天下雨的可能性比较大 D．明天下雨的可能性比较小 ‎6．如图，已知△ABC的顶点B的坐标是(2，1)，将△ABC 向左平移两个单位后，点B平移到B1，则B1的坐标是（ ）．‎ A．(4， 1) B．(0，1) ‎ C．(－1，1) D．(1，0)‎ ‎7．随着微电子制造技术的不断进步，电子元件的尺寸大幅度缩小，在芯片上某种电子元件大约只占0.000 000 7 (平方毫米)，这个数用科学记数法表示为（ ）. ‎ A．7×10－6 B．0.7×10－‎6 C．7×10－7 D．70×10－8 ‎ ‎8．在2008年的世界无烟日（‎5月31日），小华学习小组为了解本地区大约有多少成年人吸烟，随机调查了100个成年人，结果其中有15个成年人吸烟．对于这个关于数据收集与处理的问题，下列说法正确的是（ ）．‎ A．调查的方式是普查 B．本地区只有85个成年人不吸烟 C．样本是15个吸烟的成年人 D．本地区约有15%的成年人吸烟 ‎9．如图，将三角尺ABC（其中∠ABC＝60°，∠C＝90°）绕B点按顺时针方向转动一个角度到A1BC1的位置，使得点A，B，C1在同一条直线上，那么这个角度等于（ ）．‎ A．120° B．90° C．60° D．30°‎ ‎(第10题)‎ ‎10．如图，房间地面的图案是用大小相同的黑、白正方形镶嵌而成．图中，第1个黑色 形由3个正方形组成，第2个黑色形由7个正方形组成，……那么组成第6个 黑色形的正方形个数是（ ）．‎ A．22 B．‎23 C．24 D．25‎ ‎(第12题)‎ 二、填空题：（请将解答结果填写在第II卷上指定的位置．本大题共5小题，每题3分，计15分）‎ ‎11．化简：＋（5－）= ．‎ ‎12．翔宇学中的铅球场如图所示，已知扇形AOB的面积是‎36米2，‎ 的长度为‎9米，那么半径OA＝ 米．‎ ‎13．从围棋盒中抓出一大把棋子，所抓出棋子的个数是奇数的概率为 ．‎ ‎14．如图，奥运五环旗上的五个环可以近似地看成五个圆，这五个圆反映 出的圆与圆的位置关系有 或者 ．‎ ‎(第14题)‎ ‎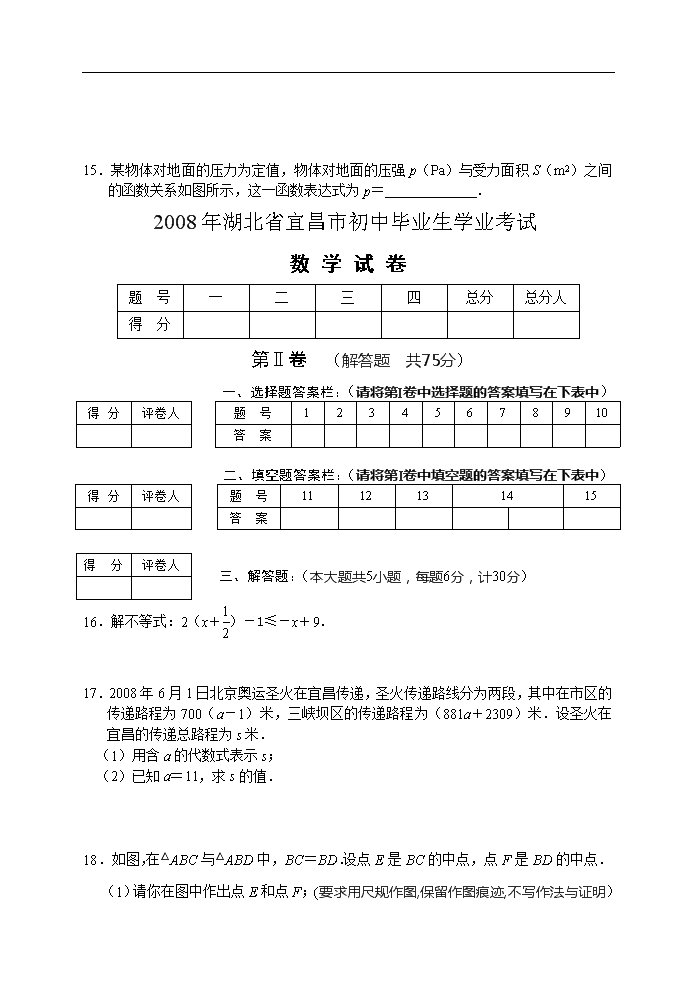15．某物体对地面的压力为定值，物体对地面的压强p（Pa）与受力面积S（m2‎ ‎）之间的函数关系如图所示，这一函数表达式为p＝ ．‎ ‎2008年湖北省宜昌市初中毕业生学业考试 数 学 试 卷 题 号 一 二 三 四 总分 总分人 得 分 第Ⅱ卷 （解答题 共75分）‎ 一、选择题答案栏：（请将第I卷中选择题的答案填写在下表中）‎ 得 分 评卷人 题 号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答 案 二、填空题答案栏：（请将第I卷中填空题的答案填写在下表中）‎ 得 分 评卷人 题 号 ‎11‎ ‎12‎ ‎13‎ ‎14‎ ‎15‎ 答 案 得 分 评卷人 三、解答题：（本大题共5小题，每题6分，计30分）‎ ‎16．解不等式：2（x＋）－1≤－x＋9．‎ ‎17．‎2008年6月1日北京奥运圣火在宜昌传递，圣火传递路线分为两段，其中在市区的传递路程为700（a－1）米，三峡坝区的传递路程为（‎881a＋2309）米．设圣火在宜昌的传递总路程为s米．‎ ‎（1）用含a的代数式表示s；‎ ‎（2）已知a＝11，求s的值．‎ ‎18．如图，在△ABC与△ABD中，BC＝BD．设点E是BC的中点，点F是BD的中点．‎ ‎（1）请你在图中作出点E和点F；(要求用尺规作图,保留作图痕迹,不写作法与证明）‎ ‎(第18题)‎ ‎（2）连接AE，AF．若∠ABC＝∠ABD，请你证明△ABE≌△ABF．‎ ‎(第19题)‎ ‎19．如图，某种雨伞的伞面可以看成由12块完全相同的等腰三角形布料缝合而成，量得其中一个三角形OAB的边OA＝OB＝‎56cm．‎ ‎（1）求∠AOB的度数；‎ ‎（2）求△OAB的面积．（不计缝合时重叠部分的面积）‎ ‎ ‎ ‎20．为积极响应党中央关于支援5·12汶川地震灾区抗震救灾的号召，宜佳工厂日夜连续加班，计划为灾区生产m顶帐篷．生产过程中的剩余生产任务y（顶）与已用生产时间x（时）之间的关系如图所示.‎ ‎（1）求变量y与x之间的关系式；‎ ‎（2）求m的值. ‎ 得 分 评卷人 四、解答题：（本大题共5小题，第21，22题每题8分，第23题 ‎9分，第24，25题每题10分，计45分）‎ ‎(第21题)‎ ‎21．如图，⊙O的半径OD经过弦AB(不是直径)的中点C，过AB的延长线上一点P作⊙O的切线PE，E为切点，PE∥OD；延长直径AG交PE于点H；直线DG交OE于点F，交PE于点K．‎ ‎（1）求证：四边形OCPE是矩形；‎ ‎（2）求证：HK＝HG；‎ ‎（3）若EF＝2，FO＝1，求KE的长．‎ ‎22．如图1，草原上有A，B，C三个互通公路的奶牛养殖基地，B与C之间距离为100千米，C在B的正北方，A在C的南偏东47°方向且在B的北偏东43°方向．A地每年产奶3万吨；B地有奶牛9 000头，平均每头牛的年产奶量为3吨；C地养了三种奶牛，其中黑白花牛的头数占20％，三河牛的头数占35％，其他情况反映在图2，图3中．‎ ‎(图1) (图2) (图3)‎ ‎(第22题)‎ ‎（1）通过计算补全图3；‎ ‎（2）比较B地与C地中，哪一地平均每头牛的年产奶量更高？‎ ‎（3）如果从B，C两地中选择一处建设一座工厂解决三个基地的牛奶加工问题，当运送一吨牛奶每千米的费用都为1元（即1元/吨·千米时，那么从节省运费的角度考虑，应在何处建设工厂？‎ ‎23．如图，在Rt△ABC中，AB＝AC，P是边AB（含端点）上的动点．过P作BC的垂线PR，R为垂足，∠PRB的平分线与AB相交于点S，在线段RS上存在一点T，若以线段PT为一边作正方形PTEF，其顶点E，F恰好分别在边BC，AC上．‎ ‎（1）△ABC与△SBR是否相似，说明理由； ‎ ‎（2）请你探索线段TS与PA的长度之间的关系；‎ ‎(第23题)‎ ‎（3）设边AB＝1，当P在边AB（含端点）上运动时，请你探索正方形PTEF的面积y的最小值和最大值．‎ ‎24．用煤燃烧发电时，所说的标准煤是指含热量为7 000大卡/千克的煤．生产实际中，一般根据含热量相等，把所需标准煤的用煤量折合成含相同热量的实际用煤量来计算．（“大卡/千克”为一种热值单位）‎ 光明电厂生产中每发一度电需用标准煤0.36千克，现有煤矸石和大同煤两种可选为生产实际用煤，这两种煤的基本情况见下表： ‎ 煤的 品种 含热量 ‎（大卡/千克）‎ 只用本种煤每发一度电的用煤量 ‎（千克/度）‎ 平均每燃烧一吨煤发电的生产成本 购煤费用 ‎（元/吨）‎ 其他费用 ‎（元/吨）‎ 煤矸石 ‎1 000‎ ‎2.52‎ ‎150‎ a（a>0）‎ 大同煤 ‎6 000‎ m ‎600‎ a2 ‎ ‎（1）求生产中只用大同煤每发一度电的用煤量（即表中m的值）；‎ ‎（2）根据环保要求，光明电厂在大同煤中掺混煤矸石形成含热量为5 000大卡/千克的混合煤来燃烧发电，若使用这种混合煤比全部使用大同煤每发1 000度电的生产成本增加了5.04元，求表中a的值．（生产成本＝购煤费用＋其它费用）‎ ‎25．如图1，已知四边形OABC中的三个顶点坐标为O(0，0)，A(0，n)，C(m，0)．动点P从点O出发依次沿线段OA，AB，BC向点C移动，设移动路程为z，△OPC的面积S随着z的变化而变化的图象如图2所示．m，n是常数， m＞1，n＞0．‎ ‎（1）请你确定n的值和点B的坐标；‎ ‎(图1) (图2) ‎ ‎(第25题)‎ ‎（2）当动点P是经过点O，C的抛物线y＝ax＋bx＋c的顶点，且在双曲线y＝上时，求这时四边形OABC的面积．‎ ‎2008年湖北省宜昌市初中学业考试 数学试卷参考答案及评分说明 ‎(一)阅卷评分说明 ‎1.正式阅卷前先进行试评，在试评中认真阅读参考答案，明确评分标准，不得随意拔高或降低评分标准. 试评的试卷必须在阅卷后期全部予以复查，防止阅卷前后期评分标准宽严不一致.‎ ‎2.评分方式为分小题分步累计评分，解答过程的某一步骤发生笔误，只要不降低后继部分的难度，而后继部分再无新的错误，后继部分可评应得分数的50%；若是几个相对独立的得分点，其中一处错误不影响其它得分点的评分.‎ ‎3.最小记分单位为1分，不得将评分标准细化至1分以下(即不得记小数分).‎ ‎4.解答题题头一律记该题的实际得分，不得用记负分的方式记分. 对解题中的错误须用红笔标出，并继续评分，直至将解题过程评阅完毕，并在最后得分点处标上该题实际得分.‎ ‎5.本参考答案只给出一种或几种解法，凡有其它正确解法都应参照本评分说明分步确定得分点，并同样实行分小题分步累计评分.‎ ‎6.合理精简解题步骤者，其简化的解题过程不影响评分.‎ ‎(二)参考答案及评分标准 一、选择题:(每题3分，共30分)‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 C D A D C B C D A B 二、填空题:(每题3分，共15分)‎ 题 号 ‎11‎ ‎12‎ ‎13‎ ‎14‎ ‎15‎ 答 案 ‎5‎ ‎8‎ (或0.5)‎ 相交；外离 说明：第14题答对一种情况评2分，将外离答为相离不扣分；‎ 第15题填写p＝不扣分，填写p＝扣1分.‎ 三、解答题：(本大题有5题，每题6分，计30分)‎ ‎16．解：去括号得 2x＋1－1≤－x＋9，(2分)‎ 移项、合并同类项得3x≤9，(4分)‎ 两边都除以3得x≤3. (6分)‎ ‎17．解：(1)s＝700(a－1)＋(‎881a＋2309)(3分)‎ ‎＝1 581 a ＋1 609.‎ ‎(2)a＝11时，‎ s＝1 ‎581 a ＋1609＝1 581×11 ＋1 609(4分)‎ ‎＝19 000.(6分)‎ ‎[或s＝700(a－1)＋(‎881a＋2 309)‎ ‎＝700(11－1)＋881×11＋2 309(4分)‎ ‎＝19 000.(6分) ]‎ ‎18.解：(1)能看到“分别以B，C为圆心，适当长为半径画弧，两弧交于点M、N，(1分)连接MN，交BC于E”的痕迹，(2分)能看到用同样的方法“作出另一点F(或以B为圆心，BE为半径画弧交BD于点F)”的痕迹.(3分)‎ ‎(凡正确作出点E,F中的一个后，另一个只要在图上标注了大致位置即可评3分)‎ ‎(2)∵BC＝BD，E，F分别是BC，BD的中点，‎ ‎∴BE＝BF，(4分)‎ ‎∵AB＝AB，∠ABC＝∠ABD,(5分)‎ ‎∴△ABE≌△ABF.(6分)‎ ‎19.解：(1)∠AOB＝360÷12＝30 (度) . (2分)‎ ‎(2)作高BD，在Rt△BDO中，∠AOB＝30°，OB＝‎‎56cm ‎∴BO＝2BD，BD＝28，(4分)（或写成DB＝BOsin30°＝28）‎ ‎∴△OAB的面积＝×OA×BD＝784.(6分)(cm2) (漏掉单位不扣分)‎ ‎20．解：(1)设y与x的关系式为y＝kx＋b，(1分)‎ 由图象知，点(30，400)，(50，0)在y＝kx＋b的图象上，(2分)‎ 将两点的坐标代入上述关系式，解得k＝－20，b＝1 000，(3分)‎ 所以y与x的关系式为y＝－20x＋1 000.(4分)‎ ‎(2)当x＝0时，y＝1 000，所以m的值是1 000. (6分)‎ ‎(第21题)‎ 四、解答题：(本大题共5小题，第21、22小题每题8分，第23题9分，第24、25小题每题10分，计45分)‎ ‎21.解：(1)∵AC＝BC，AB不是直径，‎ ‎∴OD⊥AB，∠PCO＝90°(1分)‎ ‎∵PE∥OD,∴∠P＝90°，‎ ‎∵PE是切线，∴∠PEO＝90°，(2分)‎ ‎∴四边形OCPE是矩形.(3分)‎ ‎(2)∵OG＝OD,∴∠OGD＝∠ODG.‎ ‎∵PE∥OD,∴∠K＝∠ODG.(4分)‎ ‎(第22题)‎ ‎∵∠OGD＝∠HGK,∴∠K＝∠HGK,‎ ‎∴HK＝HG.(5分)‎ ‎(3)∵EF＝2，OF＝1,∴EO＝DO＝3.(6分)‎ ‎∵PE∥OD，∴∠KEO＝∠DOE，∠K＝∠ODG.‎ ‎∴△OFD∽△EFK，(7分)∴EF∶OF＝KE∶OD＝2∶1,‎ ‎∴KE＝6.(8分)‎ ‎22.解：(1)只要条形高度约在3 500左右即可评1分 ‎(注：条形图上未标注数字3 500不扣分)‎ ‎(2 )C地每头牛的年平均产奶量为 ‎ ‎（或5×20％＋3.1×35％＋2.1×45％）‎ ‎＝3.03 (吨) ，(2分)‎ 而B地每头牛的年平均产奶量为3 吨，‎ 所以，C地每头牛的年平均产奶量比B地的高. (3分)‎ ‎(3)由题意：C地每年产奶量为10 000×3.03＝3.03万吨，‎ B地每年产奶量为9 000×3＝2.7万吨，A地每年产奶量为3万吨.(4分)‎ ‎(注：此处为独立得分点，计算出B,C中一地的年产奶量即可评1分)‎ 由题意，∠CBA＝43°,∠ACB＝47°，∴∠BAC＝90°，(5分)‎ ‎∵BC＝100(千米)，‎ ‎∴AB＝100×sin47°≈100×0.731＝73.1(千米) ，‎ ‎∴AC＝100×sin43°≈100×0.682＝68.2(千米)，(6分)‎ ‎(注：此处为独立得分点，计算出上面两个结果中任一个即可评1分)‎ 如果在B地建厂，则每年需运费 W1＝73.1×3×1＋100×3.03×1＝219.3＋303＝522.3(万元)(7分)‎ 如果在C地建厂，则每年需运费 W2＝68.2×3×1＋100×2.7×1＝204.6＋270＝474.6(万元)‎ 而522.3>474.6 ‎ 答：从节省运费的角度考虑，应在C地建设工厂.(8分)‎ ‎23．解：(1)‎(第23题图1)‎ ∵RS是直角∠PRB的平分线，∴∠PRS＝∠BRS＝45°.‎ 在△ABC与△SBR中，∠C＝∠BRS＝45°，∠B是公共角，‎ ‎∴△ABC∽△SBR..(1分) ‎ ‎(2)线段TS的长度与PA相等.(2分)‎ ‎∵四边形PTEF是正方形，‎ ‎∴PF＝PT，∠SPT＋∠FPA＝180°－∠TPF＝90°,‎ 在Rt△PFA中，∠PFA ＋∠FPA＝90°,‎ ‎∴∠PFA＝∠TPS，‎ ‎∴Rt△PAF≌Rt△TSP，∴PA＝TS.(3分)‎ 当点P运动到使得T与R重合时，‎ 这时△PFA与△TSP都是等腰直角三角形且底边相等，即有PA＝TS. ‎ ‎(第23题图2)‎ ‎(第23题图3)‎ ‎(若下面解题中没有求出x的取值范围是0≤x≤，‎ 以上的讨论可评1分)‎ 由以上可知，线段ST的长度与PA相等.‎ ‎ (3)由题意，RS是等腰Rt△PRB的底边PB上的高，‎ ‎∴PS＝BS, ∴BS＋PS＋PA＝1, ∴PS＝.(4分)‎ 设PA的长为x，易知AF=PS，‎ 则y＝PF＝PA＋PS,得y＝x＋(),‎ 即y＝，(5分)‎ 根据二次函数的性质，当x＝时，y有最小值为.(6分)‎ 如图2，当点P运动使得T与R重合时，PA＝TS为最大.‎ 易证等腰Rt△PAF≌等腰Rt△PSR≌等腰Rt△BSR，‎ ‎∴PA＝.‎ 如图3，当P与A重合时，得x＝0.‎ ‎∴x的取值范围是0≤x≤.(7分) (此处为独立得分点，只要求出x≤即可得1分)‎ ‎∴①当x的值由0增大到时，y的值由减小到(8分)‎ ‎∴②当x的值由增大到时，y的值由增大到.(8分)‎ ‎(说明：①②任做对一处评1分，两处全对也只评一分)‎ ‎∵≤≤，∴在点P的运动过程中，‎ 正方形PTEF面积y的最小值是，y的最大值是.(9分)‎ ‎24.解：(1)光明电厂生产1度电所用的大同煤为m千克，而标准煤用量为0.36千克，‎ 由题意，得0.36×7 000＝m×6 000，解得 m＝0.42(2分)‎ ‎（或6 000 m＝1 000×2.52）‎ 煤的 品种 含热量 ‎(大卡/千克)‎ 只用本种煤每发一度电的用煤量 ‎(千克/度)‎ 平均每燃烧一吨煤发电的生产成本 购煤费用 ‎(元/吨)‎ 其他费用 ‎(元/吨)‎ 煤矸石 ‎1 000‎ ‎2.52‎ ‎150‎ a (a>0)‎ 大同煤 ‎6 000‎ ‎0.42‎ ‎600‎ a2‎ 混合煤 ‎5 000‎ ‎0.504‎ ‎510‎ ‎0.8a‎2＋‎‎0.2 a ‎(2)设1吨含热量为5000大卡/千克的混合煤中含p吨大同煤和q吨煤矸石.‎ 则 ，解得，(3分)‎ ‎(计算出混合煤中大同煤占80%，煤矸石占20%，或比例为4：1，即评1分)‎ 故购买1吨混合煤费用为0.8×600＋0.2×150＝510(元)，‎ 其他费用为0.8a＋0.2 a2 元. (4分)‎ 设光明电厂生产1度电用的混合煤为h千克，‎ 则, 解得h＝0.504(千克). (5分)‎ ‎[或：设生产1千度电用的混合煤中含x吨大同煤和y吨煤矸石.‎ 则 ，解得，(5分)]‎ 生产1千度电用的大同煤：1 000×0.42＝420 (千克)＝0.42(吨)，‎ 生产1千度电用的混合煤：1 000×0.504＝504(千克)＝0.504(吨)，‎ 由题意可知数量关系：‎ ‎5.04＝平均每燃烧1吨混合煤发电的生产成本×生产1千度电所用混合煤 ‎－平均每燃烧1吨大同煤发电的生产成本×生产1千度电所用大同煤 (※6分)‎ 即：(510＋0.8a2＋0.2 a)×0.504－(600＋a2)×0.42＝5.04 (8分)‎ ‎（所列方程正确，※未叙述仍评8分）‎ 化简并整理，得 0.1008 a—0.0168 a2＝0. (9分)‎ ‎（也可以直接写出方程：‎ ‎ ）‎ 解得 a1＝6， a2＝0，(不合题意，应舍去)‎ 所以表中a的值为6. (10分)‎ ‎25.解：(1) 从图中可知，当P从O向A运动时，△POC的面积S＝mz， z由0逐步增大到2,则S由0逐步增大到m，故OA＝2，n＝2 . (1分)‎ 同理，AB＝1，故点B的坐标是(1，2).(2分)‎ ‎(2)解法一：‎ ‎∵抛物线y＝ax＋bx＋c经过点O(0，0)，C(m ，0),∴c＝0，b＝－am，(3分)‎ ‎∴抛物线为y＝ax－amx，顶点坐标为(，－am2).(4分)‎ ‎(25题图1)‎ 如图1，设经过点O，C，P的抛物线为l.‎ 当P在OA上运动时，O,P都在y轴上，‎ 这时P,O,C三点不可能同在一条抛物线上，‎ ‎∴这时抛物线l不存在, 故不存在m的值..①‎ 当点P与C重合时，双曲线y＝不可能经过P,‎ 故也不存在m的值.②(5分)‎ ‎(说明：①②任做对一处评1分，两处全对也只评一分)‎ 当P在AB上运动时，即当02,与 x＝≤1不合，舍去.(6分)③‎ 容易求得直线BC的解析式是：，(7分)‎ 当P在BC上运动，设P的坐标为 (x,y)，当P是顶点时 x＝，‎ 故得y＝＝，顶点P为(，)，‎ ‎∵1< x＝2，又∵P在双曲线y＝上，‎ 于是，×＝，化简后得5m－22m＋22＝0, ‎ 解得,,(8分)‎ 与题意2