- 957.72 KB
- 2021-05-13 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
学生: 科目: 数 学 教师:
课 题
压轴题训练:圆
教学内容
知识框架
一、圆的概念
集合形式的概念: 1、 圆可以看作是到定点的距离等于定长的点的集合;
2、圆的外部:可以看作是到定点的距离大于定长的点的集合;
3、圆的内部:可以看作是到定点的距离小于定长的点的集合
轨迹形式的概念:
1、圆:到定点的距离等于定长的点的轨迹就是以定点为圆心,定长为半径的圆;
(补充)2、垂直平分线:到线段两端距离相等的点的轨迹是这条线段的垂直平分线(也叫中垂线);
3、角的平分线:到角两边距离相等的点的轨迹是这个角的平分线;
4、到直线的距离相等的点的轨迹是:平行于这条直线且到这条直线的距离等于定长的两条直线;
5、到两条平行线距离相等的点的轨迹是:平行于这两条平行线且到两条直线距离都相等的一条直线。
二、点与圆的位置关系
1、点在圆内 点在圆内;
2、点在圆上 点在圆上;
3、点在圆外 点在圆外;
三、直线与圆的位置关系
1、直线与圆相离 无交点;
2、直线与圆相切 有一个交点;
3、直线与圆相交 有两个交点;
四、圆与圆的位置关系
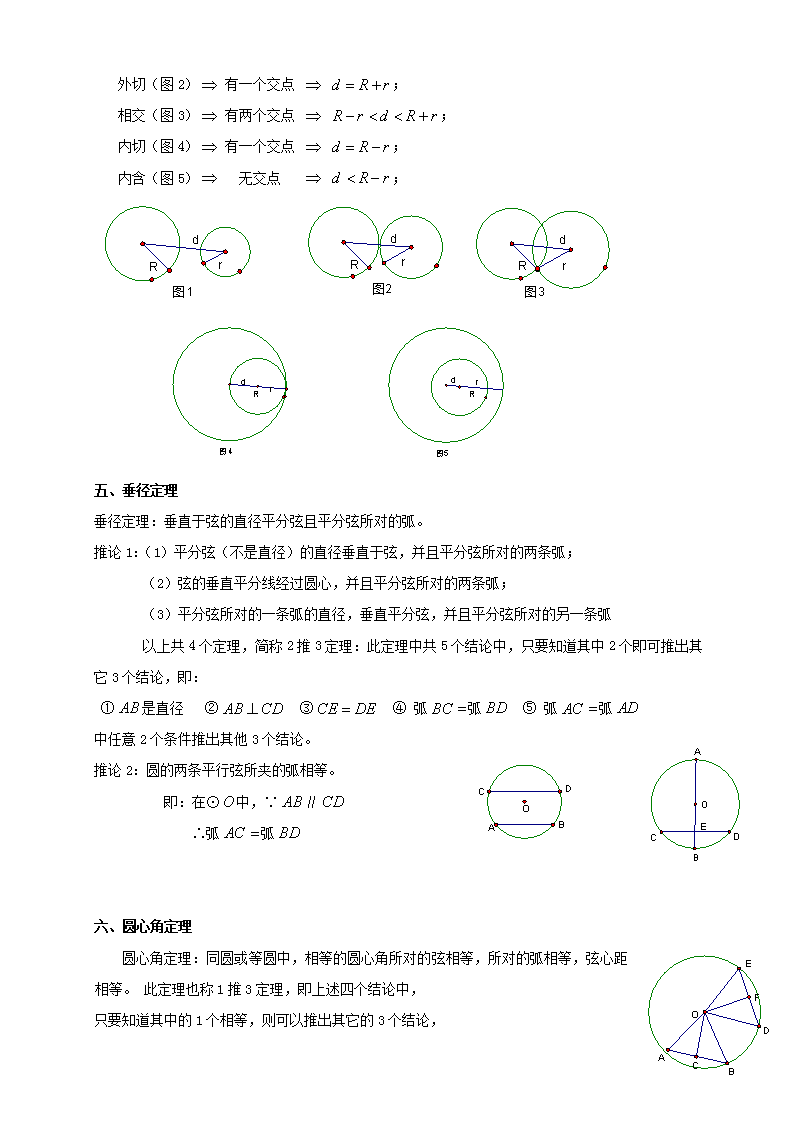
外离(图1) 无交点 ;
外切(图2) 有一个交点 ;
相交(图3) 有两个交点 ;
内切(图4) 有一个交点 ;
内含(图5) 无交点 ;
五、垂径定理
垂径定理:垂直于弦的直径平分弦且平分弦所对的弧。
推论1:(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;
(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;
(3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧
以上共4个定理,简称2推3定理:此定理中共5个结论中,只要知道其中2个即可推出其它3个结论,即:
①是直径 ② ③ ④ 弧弧 ⑤ 弧弧
中任意2个条件推出其他3个结论。
推论2:圆的两条平行弦所夹的弧相等。
即:在⊙中,∵∥
∴弧弧
六、圆心角定理
圆心角定理:同圆或等圆中,相等的圆心角所对的弦相等,所对的弧相等,弦心距相等。 此定理也称1推3定理,即上述四个结论中,
只要知道其中的1个相等,则可以推出其它的3个结论,
即:①;②;
③;④ 弧弧
七、圆周角定理
1、圆周角定理:同弧所对的圆周角等于它所对的圆心的角的一半。
即:∵和是弧所对的圆心角和圆周角
∴
2、圆周角定理的推论:
推论1:同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧是等弧;
即:在⊙中,∵、都是所对的圆周角
∴
推论2:半圆或直径所对的圆周角是直角;圆周角是直角所对的弧是半圆,所对的弦是直径。
即:在⊙中,∵是直径 或∵
∴ ∴是直径
推论3:若三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形。
即:在△中,∵
∴△是直角三角形或
注:此推论实是初二年级几何中矩形的推论:在直角三角形中斜边上的中线等于斜边的一半的逆定理。
八、圆内接四边形
圆的内接四边形定理:圆的内接四边形的对角互补,外角等于它的内对角。
即:在⊙中,
∵四边形是内接四边形
∴
九、切线的性质与判定定理
(1)切线的判定定理:过半径外端且垂直于半径的直线是切线;
两个条件:过半径外端且垂直半径,二者缺一不可
即:∵且过半径外端
∴是⊙的切线
(2)性质定理:切线垂直于过切点的半径(如上图)
推论1:过圆心垂直于切线的直线必过切点。
推论2:过切点垂直于切线的直线必过圆心。
以上三个定理及推论也称二推一定理:
即:①过圆心;②过切点;③垂直切线,三个条件中知道其中两个条件就能推出最后一个。
十、切线长定理
切线长定理:
从圆外一点引圆的两条切线,它们的切线长相等,这点和圆心的连线平分两条切线的夹角。
即:∵、是的两条切线
∴
平分
十一、圆幂定理
(1)相交弦定理:圆内两弦相交,交点分得的两条线段的乘积相等。
即:在⊙中,∵弦、相交于点,
∴
(2)推论:如果弦与直径垂直相交,那么弦的一半是它分直径所成的两条线段的比例中项。
即:在⊙中,∵直径,
∴
(3)切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。
即:在⊙中,∵是切线,是割线
∴
(4)割线定理:从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等(如上图)。
即:在⊙中,∵、是割线
∴
十二、两圆公共弦定理
圆公共弦定理:两圆圆心的连线垂直并且平分这两个圆的的公共弦。
如图:垂直平分。
即:∵⊙、⊙相交于、两点
∴垂直平分
十三、圆的公切线
两圆公切线长的计算公式:
(1)公切线长:中,;
(2)外公切线长:是半径之差; 内公切线长:是半径之和 。
十四、圆内正多边形的计算
(1)正三角形
在⊙中△是正三角形,有关计算在中进行:;
(2)正四边形
同理,四边形的有关计算在中进行,:
(3)正六边形
同理,六边形的有关计算在中进行,.
十五、扇形、圆柱和圆锥的相关计算公式
1、扇形:(1)弧长公式:;
(2)扇形面积公式:
:圆心角 :扇形多对应的圆的半径 :扇形弧长 :扇形面积
2、圆柱:
(1)圆柱侧面展开图
=
(2)圆柱的体积:
(2)圆锥侧面展开图
(1)=
(2)圆锥的体积:
【例题精讲】
1如图12所示,四边形ABCD是以O为圆心,AB为直径的半圆的内接四边形,
对角线AC、BD相交于点E。
(1)求证:△DEC~△AEB;
(2)当∠AED=60°时,求△DEC与△AEB的面积比。
2 如图13,已知等边三角形ABC,以边BC为直径的半圆与边AB、AC分别交于点D、
点E,过点E作EF⊥AB,垂足为点F。
(1)判断EF与⊙O的位置关系,并证明你的结论;
(2)过点F作FH⊥BC,垂足为点H,若等边△ABC的边长为8,求FH的长。
(结果保留根号)
3 已知:如图,在中,,点在上,以为圆心,长
D
C
O
A
B
E
为半径的圆与分别交于点,且.
(1)判断直线与的位置关系,并证明你的结论;
(2)若,,求的长.
4 四川省成都 如图,已知⊙O的半径为2,以⊙O的弦AB为直径作⊙M,点C是⊙O优弧上的一个动点(不与点A、点B重合).连结AC、BC,分别与⊙M相交于点D、点E,连结DE.若AB=2
.
(1)求∠C的度数;
(2)求DE的长;
(3)如果记tan∠ABC=y,=x(00),求sin∠CAB.
A
B
C
E
D
O
M
3 已知:如图,在半径为4的⊙O中,AB,CD是两条直径,M为OB的中点,
CM的延长线交⊙O于点E,且EM>MC.连结DE,DE=.
(1) 求证:;
(2) 求EM的长;
(3)求sin∠EOB的值.
4 如图,已知⊙O的直径AB=2,直线m与⊙O相切于点A,P为⊙O上一动点
(与点A、点B不重合),PO的延长线与⊙O相交于点C,过点C的切线与直线
m相交于点D.
(1)求证:△APC∽△COD.
(2)设AP=x,OD=y,试用含x的代数式表示y.
(3)试探索x为何值时,△ACD是一个等边三角形.
C
B
O
A
D
5 如图,在以O为圆心的两个同心圆中,AB经过圆心O,且与小圆相交于点A、
与大圆相交于点B.小圆的切线AC与大圆相交于点D,且CO平分∠ACB.
(1)试判断BC所在直线与小圆的位置关系,并说明理由;
(2)试判断线段AC、AD、BC之间的数量关系,并说明理由;
(3)若,求大圆与小圆围成的圆环的面积.(结果保留π)
6 在Rt△ABC中,BC=9, CA=12,∠ABC的平分线BD交AC与点D, DE⊥DB交AB于点E.
(1)设⊙O是△BDE的外接圆,求证:AC是⊙O的切线;
(2)设⊙O交BC于点F,连结EF,求的值.
7 如图,点A,B在直线MN上,AB=11厘米,⊙A,⊙B的半径均为1厘米.⊙A以每秒2厘米的速度自左向右运动,与此同时,⊙B的半径也不断增大,其半径r(厘米)与时间t(秒)之间的关系式为r=1+t(t≥0).
A
B
N
M
(1)试写出点A,B之间的距离d(厘米)
与时间t(秒)之间的函数表达式;
(2)问点A出发后多少秒两圆相切?
P
B
C
D
T
N
M
A
K
(第27题图)
8 如图,在△ABC中,∠BAC=90°,BM平分∠ABC交AC于M,
以A为圆心,AM为半径作⊙A交BM于N,AN的延长线交BC于D,
直线AB交⊙A于P、K两点,作MT⊥BC于T.
(1)求证:AK=MT;
(2)求证:AD⊥BC;
C
B
A
O
F
D
E
(3)当AK=BD时,求证:.
9 如图,为的直径,于点,交于点,于点.
(1)请写出三条与有关的正确结论;
(2)当,时,求圆中阴影部分的面积.
10 如图,已知的直径垂直于弦于点,过点作交的延长线
A
D
F
E
O
C
B
G
(第10题图)
于点,连接并延长交于点,且.
(1)试问:是的切线吗?说明理由;
(2)请证明:是的中点;
(3)若,求的长.
11 如图11,⊙P与⊙O相交于A、B两点,⊙P经过圆心O,点C是⊙P的优弧上任意一点(不与点A、B重合),连结AB、AC、BC、OC。
(1)指出图中与∠ACO相等的一个角;
(2)当点C在⊙P上什么位置时,直线CA与⊙O相切?请说明理由;
(3)当∠ACB=60°时,两圆半径有怎样的大小关系?请说明你的理由。
12 如图,⊙O是△ABC的外接圆,且AB=AC,点D在弧BC上运动,过点D作DE∥BC,DE交AB的延长线于点E,连结AD、BD.
(1)求证:∠ADB=∠E;(3分)
(2)当点D运动到什么位置时,DE是⊙O的切线?请说明理由.(3分)
(3)当AB=5,BC=6时,求⊙O的半径.(4分)
(第12题图)
1 如图,将△AOB置于平面直角坐标系中,其中点O为坐标原点,点A的坐标为(3,0),∠ABO=60
(1)若△AOB的外接圆与y轴交于点D,求D点坐标.
(2)若点C的坐标为(-1,0),试猜想过D、C的直线与△AOB的外接圆的位置关系,并加以说明.
(3)二次函数的图象经过点O和A且顶点在圆上,求此函数的解析式.
B1
B2
B3
A1
A2
A3
O
C3
C2
C1
图4
S2
S1
S3
2 如图(4),正方形的边长为1,以为圆心、为半径作扇形与相交于点,设正方形与扇形之间的阴影部分的面积为;然后以为对角线作正方形,又以为圆心,、为半径作扇形,与相交于点,设正方形与扇形之间的阴影部分面积为;按此规律继续作下去,设正方形与扇形之间的阴影部分面积为.
(1)求;
(2)写出;
(3)试猜想(用含的代数式表示,为正整数).
3 (10分)如图,点I是△ABC的内心,线段AI的延长线交△ ABC的外接圆于点D,交BC边于点E.
(1)求证:ID=BD;
(2)设△ABC的外接圆的半径为5,ID=6,,,当点A在优弧上运动时,求与的函数关系式,并指出自变量的取值范围.
4 如图,点A,B,C,D是直径为AB的⊙O上四个点,C是劣弧的中点,AC交BD于点E, AE=2, EC=1.
(第4题图)
(1)求证:∽;
(2)试探究四边形ABCD是否是梯形?若是,请你给予
证明并求出它的面积;若不是,请说明理由.
(3)延长AB到H,使BH =OB.
求证:CH是⊙O的切线.
5 如图10,半圆O为△ABC的外接半圆,AC为直径,D为上的一动点.
(1)问添加一个什么条件后,能使得?请说明理由;
(2)若AB∥OD,点D所在的位置应满足什么条件?请说明理由;
(3)如图11,在 (1)和(2)的条件下,四边形AODB是什么特殊的四边形?证明你的结论.
D
B
A
O
C
E
·
图10
D
B
A
O
C
E
图11
6
6 如图1,已知正方形ABCD的边长为,点M是AD的中点,P是线段MD上的一动点(P不与M,D重合),以AB为直径作⊙O,过点P作⊙O的切线交BC于点F,切点为E.
(1)除正方形ABCD的四边和⊙O中的半径外,图中还有哪些相等的线段(不能添加字母和辅助线)?
(2)求四边形CDPF的周长;
·
P
D
O
G
E
M
F
B
A
C
图2
(3)延长CD,FP相交于点G,如图2所示. 是否存在点P,使BF*FG=CF*OF?如果存在,试求此时AP的长;如果不存在,请说明理由.
·
M
·
A
F
C
O
P
E
D
图1
7 如图,在平面直角坐标系中,是轴正半轴上一点,与轴的正半轴交于两点,在的左侧,且的长是方程的两根,是的切线,为切点,在第四象限.
(1)求的直径.
(2)求直线的解析式.
(3)在轴上是否存在一点,使是等腰三角形,若存在请在图2中标出点所在位置,并画出(要求尺规作图,保留作图痕迹,不写作法,不证明,不求的坐标)若不存在,请说明理由.
图1
图2
1 已知:如图4-7,∠ACG=90°,AC=2,点B为CG边上的一个动点,连结AB,将△ACB沿AB边所在的直线翻折得到△ADB,过点D作DF⊥CG于点F.
1
图4-7
图4-8
(1) 当时,判断直线FD与以
AB为直径的⊙O的位置关系,并加以证明;
(2) 如图4-8,点B在CG上向点C运动,
直线FD与以AB为直径的⊙O交于D、H两
点,连结AH,当∠CAB=∠BAD=∠DAH时,
求BC的长
2、如图,矩形ABAD中,AB=3cm,BC=4cm,△ABC和△ADC的内切圆在AC上的切点分别为E、F,求EF的长。
3、已知:在三角形ABC中,AD为∠BAC的平分线,以C为圆心,CD为半径的半圆交BC的延长线于点E,交AD于点F,交AE于点M,且∠B=∠CAE,FE:FD=4:3
A
B
C
D
E
M
F
(1)求证:AF=DF(2)求∠AED的余弦值(3)若BD=10,求△ABC的面积。
A
B
P
C
N
E
D
O2·
·
O1
4、 已知⊙O1和⊙O2相交于A、B两点,P是⊙O1上一点,
PB的延长线交⊙O2于点D,CD的延长线交⊙O1于点N
(1) 过点A作AE∥CN交⊙O1于E,求证:PA=PE
(2)连结PN,若PB=4,BC=2,求PN的长。
5 如图,已知线段AB上一点O,以OB为半径的⊙O交线段AB于C,以线段AO为直径的半圆交⊙O于点D,过点B作AB的垂线与AD相交于点E,
(1) 求证:AE切⊙O于D;
(2) 求的值;
(3) 如果⊙O的半径为,且,求CD、OE的长;
6已知,⊙O与⊙O外切,⊙O的半径,设⊙O的半径为,
(1) 如果⊙O与⊙O的圆心距,求的值;
(2) 如果⊙O与⊙O的公切线中有两条互相垂直,并且≤,求的值;
7如图,⊙O1与⊙O2相交于A、B两点,过点B的直线交⊙O1、⊙O2于C、D, 的中点为M,AM交⊙O1于E,交CD于F,连CE、AD、DM.
(1)求证:AM·EF=DM·CE; (2)求证:;
(3)若BC=5,BD=7,CF=2DF,AM=4MF,求MF和CE的长.
8 如图,点P是⊙O上任意一点,⊙O的弦AB所在的直线与⊙P相切于点C,PF为⊙O
的直径,设⊙O与⊙P的半径分别为R和r.
(1)求证:△PCB∽△PAF; (2)求证:PA·PB=2Rr;
(3)若点D是两圆的一个交点,连结AD交⊙P于点E,当R=3r,PA=6,PB=3时,求⊙P的弦DE的长.