2020届中考数学全程演练 第二部分 图形与几何 第八单元 四边形 第26课时 多边形及其内角和 3页

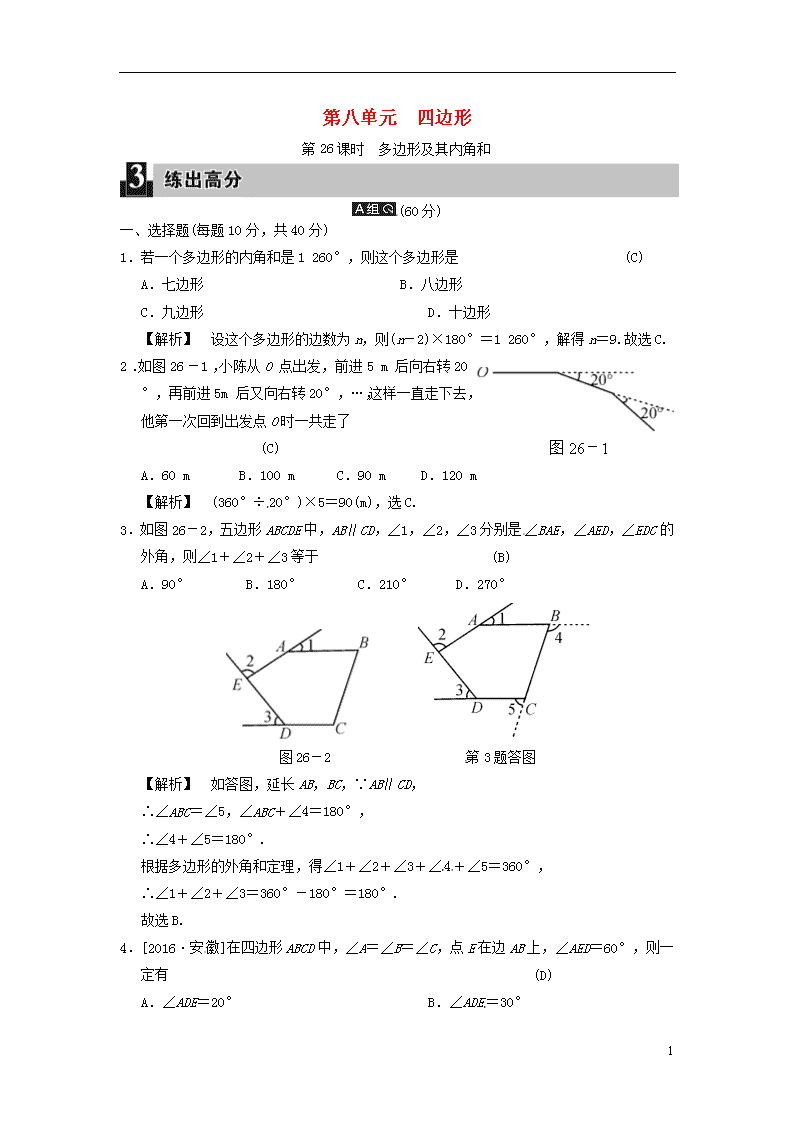
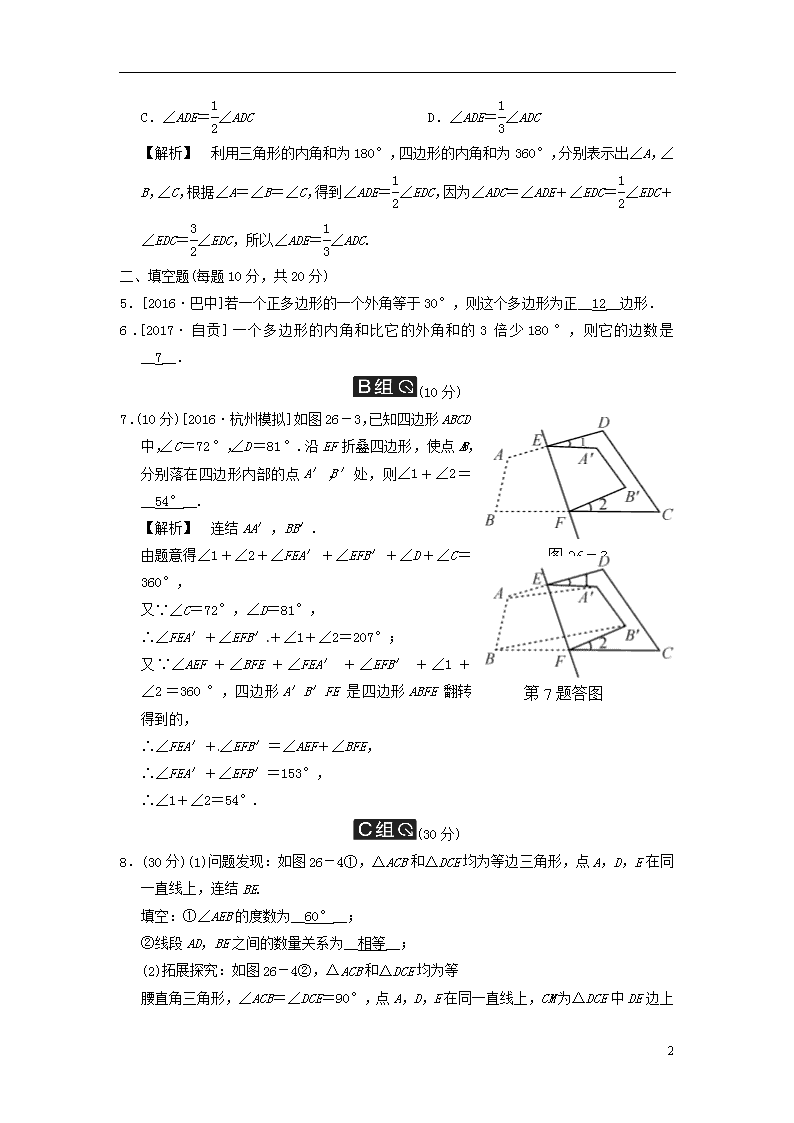
1 第八单元 四边形 第 26 课时 多边形及其内角和 (60 分) 一、选择题(每题 10 分，共 40 分) 1．若一个多边形的内角和是 1 260°，则这个多边形是 (C) A．七边形 B．八边形 C．九边形 D．十边形 【解析】 设这个多边形的边数为 n，则(n－2)×180°＝1 260°，解得 n＝9.故选 C. 2．如图 26－1，小陈从 O 点出发，前进 5 m 后向右转 20°， 再前进 5 m 后又向右转 20°，…，这样一直走下去， 他第一次回到出发点 O 时一共走了 (C) A．60 m B．100 m C．90 m D．120 m 【解析】 (360°÷20°)×5＝90(m)，选 C. 3．如图 26－2，五边形 ABCDE 中，AB∥CD，∠1，∠2，∠3 分别是∠BAE，∠AED，∠EDC 的 外角，则∠1＋∠2＋∠3 等于 (B) A．90° B．180° C．210° D．270° 图 26－2 第 3 题答图 【解析】 如答图，延长 AB，BC，∵AB∥CD， ∴∠ABC＝∠5，∠ABC＋∠4＝180°， ∴∠4＋∠5＝180°. 根据多边形的外角和定理，得∠1＋∠2＋∠3＋∠4＋∠5＝360°， ∴∠1＋∠2＋∠3＝360°－180°＝180°. 故选 B. 4．[2016·安徽]在四边形 ABCD 中，∠A＝∠B＝∠C，点 E 在边 AB 上，∠AED＝60°，则一 定有 (D) A．∠ADE＝20° B．∠ADE＝30° 图 26－1 2 C．∠ADE＝1 2 ∠ADC D．∠ADE＝1 3 ∠ADC 【解析】 利用三角形的内角和为 180°，四边形的内角和为 360°，分别表示出∠A， ∠B，∠C，根据∠A＝∠B＝∠C，得到∠ADE＝1 2 ∠EDC，因为∠ADC＝∠ADE＋∠EDC＝1 2 ∠ EDC＋∠EDC＝3 2 ∠EDC，所以∠ADE＝1 3 ∠ADC. 二、填空题(每题 10 分，共 20 分) 5．[2016·巴中]若一个正多边形的一个外角等于 30°，则这个多边形为正__12__边形． 6．[2017·自贡]一个多边形的内角和比它的外角和的 3 倍少 180°，则它的边数是__7__． (10 分) 7．(10 分)[2016·杭州模拟]如图 26－3，已知四边形 ABCD 中，∠C＝72°，∠D＝81°.沿 EF 折叠四边形，使点 A， B 分别落在四边形内部的点 A′，B′处，则∠1＋∠2 ＝__54°__. 【解析】 连结 AA′，BB′. 由题意得∠1＋∠2＋∠FEA′＋∠EFB′＋∠D＋∠C＝ 360°， 又∵∠C＝72°，∠D＝81°， ∴∠FEA′＋∠EFB′＋∠1＋∠2＝207°； 又∵∠AEF＋∠BFE＋∠FEA′＋∠EFB′＋∠1＋∠2＝ 360°，四边形 A′B′FE 是四边形 ABFE 翻转得到的， ∴∠FEA′＋∠EFB′＝∠AEF＋∠BFE， ∴∠FEA′＋∠EFB′＝153°， ∴∠1＋∠2＝54°. (30 分) 8．(30 分)(1)问题发现：如图 26－4①，△ACB 和△DCE 均为等边三角形，点 A，D，E 在同 一直线上，连结 BE. 填空：①∠AEB 的度数为__60°__； ②线段 AD，BE 之间的数量关系为__相等__； (2)拓展探究：如图 26－4②，△ACB 和△DCE 均为等 腰直角三角形，∠ACB＝∠DCE＝90°，点 A，D，E 在同一直线上，CM 为△DCE 中 DE 边上 的高，连结 BE，请判断∠AEB 的度数及线段 CM，AE，BE 之间的数量关系，并说明理由． 图 26－3 第 7 题答图 3 图 26－4 解：(1)∵∠ACB＝∠DCE，∠DCB＝∠DCB， ∴∠ACD＝∠BCE， 在△ACD 和△BCE 中， AC＝BC， ∠ACD＝∠BCE， CD＝CE， ∴△ACD≌△BCE(SAS)， ∴AD＝BE，∠CEB＝∠ADC＝180°－∠CDE＝120°， ∴∠AEB＝∠CEB－∠CED＝60°； (2)∠AEB＝90°，AE＝BE＋2CM， 理由如下： ∵△ACB 和△DCE 均为等腰直角三角形， ∴CA＝CB，CD＝CE，∠ACB＝∠DCE＝90°， ∵∠ACD＋∠DCB＝90°＝∠DCB＋∠BCE， ∴∠ACD＝∠BCE， ∴△ACD≌△BCE(SAS)， ∴AD＝BE，∠ADC＝∠BEC. ∵△DCE 为等腰直角三角形， ∴∠CDE＝∠CED＝45°， ∵点 A，D，E 在同一直线上， ∴∠ADC＝135°. ∴∠BEC＝135°， ∴∠AEB＝∠BEC－∠CED＝90°. ∵CD＝CE，CM⊥DE， ∴DM＝ME. ∵∠DCE＝90°， ∴DM＝ME＝CM， ∴AE＝AD＋DE＝BE＋2CM.