中考数学十大解题思路之等积法 3页

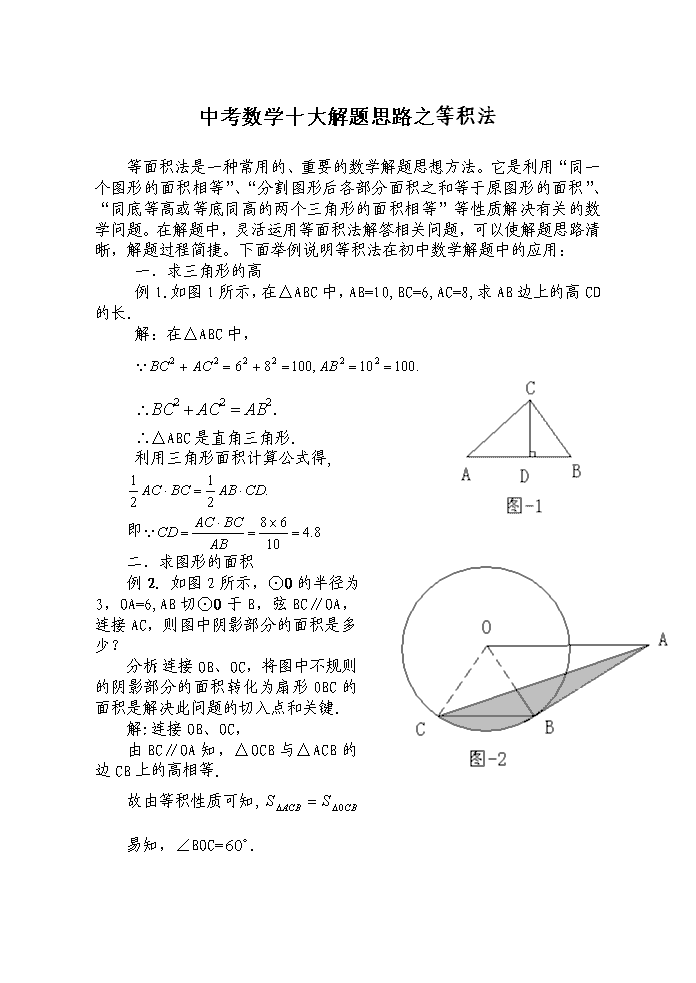
中考数学十大解题思路之等积法 等面积法是一种常用的、重要的数学解题思想方法。它是利用“同一个图形的面积相等”、“分割图形后各部分面积之和等于原图形的面积”、“同底等高或等底同高的两个三角形的面积相等”等性质解决有关的数学问题。在解题中，灵活运用等面积法解答相关问题，可以使解题思路清晰，解题过程简捷。下面举例说明等积法在初中数学解题中的应用：‎ 一．求三角形的高 例1.如图1所示，在△ABC中，AB=10,BC=6,AC=8,求AB边上的高CD的长.‎ 解：在△ABC中，‎ ‎∴△ABC是直角三角形.‎ 利用三角形面积计算公式得,‎ 即 二．求图形的面积 例2. 如图2所示，⊙O的半径为3，OA=6,AB切⊙O于B，弦BC∥OA，连接AC，则图中阴影部分的面积是多少？‎ 分析：连接OB、OC，将图中不规则的阴影部分的面积转化为扇形0BC的面积是解决此问题的切入点和关键.‎ 解:连接OB、OC，‎ 由BC∥OA知，△OCB与△ACB的边CB上的高相等.‎ 故由等积性质可知,‎ 易知，∠BOC=.‎ 所以.‎ 三.求三角形内切圆半径 例3.如图3所示,已知⊙O是△ABC的内切圆，∠C=，AC=4，BC=3. 求 ‎⊙O的半径.‎ 解:设⊙O的半径为r，连接0A、0B、OC、OE、OF、OG..‎ ‎∵⊙O是△ABC的内切圆，‎ ‎∴OG⊥AB，OE⊥BC，OF⊥AC，且 OE=OF=OG=r.‎ 在Rt△ABC中，由勾股定理，得 于是由，得 即 ‎ ‎∴‎ 四．求函数的解析式 例4．如图4所示，线段AB=8，直线m与⊙o相切于点 D,且m∥AB，P是直线m上的一点,PB交以AB为直径的圆于C,连结AC.设PB=x,AC=y,求y与x的函数关系式.‎ 分析：因为AB是⊙O的直径，所以AC⊥BP，又因为把直线m与⊙o相切于点 D,且m∥AB，所以DO⊥AB,BP和AC看成三角形的底和高，于是很自然地连接AP、OD，利用同一个三角形的面积相等的性质，就可以得到x与y的关系.‎ 解:连结AP，‎ ‎∵AB是⊙O的直径，‎ ‎∴AC⊥BP.‎ 又∵直线m与⊙o相切于点 D,且m∥AB，‎ ‎∴DO⊥AB 即△ABP的AB边上的高是4,‎ ‎∴即xy=8×4.‎ ‎ (x＞4).‎ 五.在探究规律题中的应用 例5.如图-5所示，将一个边长为1的正方形平均分成两个面积是矩形，又将一个面积为矩形平均分成两个面积是的矩形，再将一个面积为的矩形平局分成两个面积是的矩形，如此进行分割下去，如果分割n次后，按图中揭示的规律计算：‎ ‎ ‎ 分析：分割图形后各部分面积之和等于原图形的面积根,得 于是利用这个规律就可以把问题解决.‎ 解：=‎ 总之，等面积法是一种重要的数学解题思想方法。利用此法解决相关数学问题时，不但思路清晰、过程简捷，而且更能体现出知识间的相互联系，更有利于培养学生的数学思维能力，发展学生的数学能力。在数学解题教学中值得借鉴。‎