温州中考应用题第1次专题练习20160416 19页

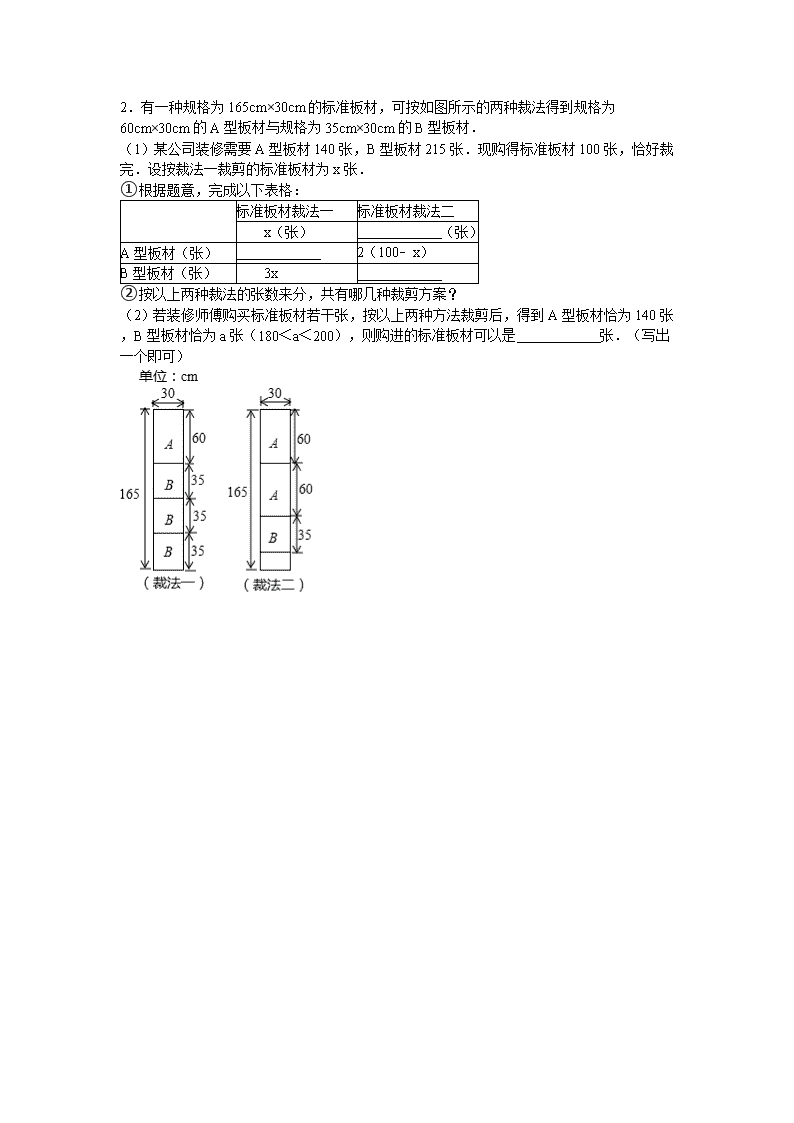
温州中考第23题第1次专题练习20160416‎ ‎　‎ 一．解答题（共10小题）‎ ‎1．某工厂用如图甲所示的长方形和正方形纸板，做成如图乙所示的竖式与横式两种长方体形状的无盖纸盒　　　　　　．‎ ‎（1）现有正方形纸板162张，长方形纸板340张．若要做两种纸盒共100个，设做竖式纸盒x个．‎ ‎①根据题意，完成以下表格：‎ 纸盒 纸板 竖式纸盒（个）‎ 横式纸盒（个）‎ ‎ x ‎100﹣x ‎ 正方形纸板（张）‎ ‎ 2（100﹣x）‎ ‎ 长方形纸板（张）‎ ‎ 4x ‎②按两种纸盒的生产个数来分，有哪几种生产方案？‎ ‎（2）若有正方形纸162张，长方形纸板a张，做成上述两种纸盒，纸板恰好用完．已知290＜a＜306．求a的值．‎ ‎2．有一种规格为165cm×30cm的标准板材，可按如图所示的两种裁法得到规格为60cm×30cm的A型板材与规格为35cm×30cm的B型板材．‎ ‎（1）某公司装修需要A型板材140张，B型板材215张．现购得标准板材100张，恰好裁完．设按裁法一裁剪的标准板材为x张．‎ ‎①根据题意，完成以下表格：‎ 标准板材裁法一 标准板材裁法二 ‎ x（张）‎ ‎　　　　　　（张）‎ A型板材（张）‎ ‎　　　　　　‎ ‎2（100﹣x）‎ B型板材（张）‎ ‎ 3x ‎　　　　　　‎ ‎②按以上两种裁法的张数来分，共有哪几种裁剪方案？‎ ‎（2）若装修师傅购买标准板材若干张，按以上两种方法裁剪后，得到A型板材恰为140张，B型板材恰为a张（180＜a＜200），则购进的标准板材可以是　　　　　　张．（写出一个即可）‎ ‎3．某校积极开展“促进有效学习”课堂教学改革实验，班内各个学习小组共设四个评价项目每月都要评奖：自主学习，课堂展示，互动点评，反馈检测，每个项目得分都按一定百分比折算后计入总分．下表为繁星、新月、初阳三个小组的得分情况（单位：分）‎ 自主学习 课堂展示 互动点评 反馈检测 繁星 ‎80‎ ‎50‎ ‎40‎ ‎70‎ 新月 ‎40‎ ‎80‎ ‎90‎ ‎35‎ 初阳 ‎40‎ ‎95‎ ‎85‎ ‎35‎ ‎（1）月底，繁星组组长猜测自主学习，课堂展示，互动点评，反馈检测这四项得分分别按10%，30%，20%，40%折算计入总分，根据猜测，求出繁星组的总分；‎ ‎（2）学校决定，总分为60分以上（包括60分）的学习小组获得优秀小组称号．现获悉新月、初阳两组的总分分别是64.5分，69.5分，繁星组的自主学习，反馈检测两项得分折算后的分数和是29分，问：繁星组能否获得优秀？‎ ‎4．今年我区为绿化行车道，计划购买甲、乙两种树苗共计n棵．设买甲种树苗x棵．有关甲、乙两种树苗的信息如图所示．‎ ‎（1）当n=500时，‎ ‎①根据信息填表（用含x代数式表示）‎ 树苗类型 甲种树苗 乙种树苗 买树苗数量（单位：棵）‎ x 买树苗的总费用（单位：元）‎ ‎②如果购买甲、乙两种树苗共用25600元，那么甲、乙两种树苗各买了多少棵？‎ ‎（2）要使这批树苗的成活率不低于92%，且使购买这两种树苗的总费用为26000元，求n的最大值．‎ ‎5．温州享有“中国笔都”之称，其产品畅销全球，某制笔企业欲将n件产品运往A，B，C三地销售，要求运往C地的件数是运往A地件数的2倍，各地的运费如图所示．设安排x件产品运往A地．‎ ‎（1）当n=200时，①根据信息填表：‎ A地 B地 C地 合计 产品件数（件）‎ x ‎2x ‎200‎ 运费（元）‎ ‎30x ‎②若运往B地的件数不多于运往C地的件数，总运费不超过4000元，则有哪几种运输方案？‎ ‎（2）若总运费为5800元，求n的最小值．‎ ‎6．2011年5月20日是第22个中国学生营养日，某校社会实践小组在这天开展活动，调查快餐营养情况．他们从食品安全监督部门获取了一份快餐的信息（如图）．根据信息，解答下列问题．‎ ‎（1）求这份快餐中所含脂肪质量；‎ ‎（2）若碳水化合物占快餐总质量的40%，求这份快餐所含蛋白质的质量；‎ ‎（3）若这份快餐中蛋白质和碳水化合物所占百分比的和不高于85%，求其中所含碳水化合物质量的最大值．‎ ‎7．2013年1月，由于雾霾天气持续笼罩我国中东部大部分地区，口罩市场出现热卖，某旗舰网店用8000元购进甲、乙两种口罩，销售完后共获利2800元，进价和售价如下表：‎ ‎ 品名 价格 甲种口罩 乙种口罩 进价（元/袋）‎ ‎20‎ ‎25‎ 售价（元/袋）‎ ‎26‎ ‎35‎ ‎（1）求该网店购进甲、乙两种口罩各多少袋？‎ ‎（2）该网店第二次以原价购进甲、乙、两种口罩，购进乙种口罩袋数不变，而购进甲种口罩袋数是第一次的2倍．甲种口罩按原售价出售，而乙种口罩让利销售．若两种口罩销售完毕，要使第二次销售活动获利不少于3680元，乙种口罩最低售价为每袋多少元？‎ ‎8．今年小芳家添置了新电器．已知今年5月份的用电量是240千瓦时．‎ ‎（1）若今年6月份用电量增长率是7月份用电量增长率的1.5倍，设今年7月份用电量增长率为x，‎ 补全下列表格内容（用含x代数式表示）‎ 月份 ‎6月份 ‎7月份 月增长率 x 用电量 ‎（单位：千瓦时）‎ ‎（2）在（1）的条件下，预计今年7月份的用电量将达到480千瓦时，求今年7月份用电量增长率x的值．（精确到1%）‎ ‎（3）若今年6月份用电量增长率是7月份用电量增长率的n倍，6月份用电量为360千瓦时，预计今年7月份的用电量将不低于500千瓦时．则n的最大值为　　　　　　．（直接写出答案）‎ ‎9．某汽车专卖店销售A，B两种型号的新能源汽车．上周售出1辆A型车和3辆B型车，销售额为96万元；本周已售出2辆A型车和1辆B型车，销售额为62万元．‎ ‎（1）求每辆A型车和B型车的售价各为多少元．‎ ‎（2）甲公司拟向该店购买A，B两种型号的新能源汽车共6辆，购车费不少于130万元，且不超过140万元．则有哪几种购车方案？‎ ‎10．为进一步建设秀美、宜居的生态环境，某村欲购买甲、乙、丙三种树美化村庄，已知甲、乙丙三种树的价格之比为2：2：3，甲种树每棵200元，现计划用210000元资金，购买这三种树共1000棵．‎ ‎（1）求乙、丙两种树每棵各多少元？‎ ‎（2）若购买甲种树的棵树是乙种树的2倍，恰好用完计划资金，求这三种树各能购买多少棵？‎ ‎（3）若又增加了10120元的购树款，在购买总棵树不变的前提下，求丙种树最多可以购买多少棵？‎ ‎　‎ 温州中考第23题第2次专题练习 参考答案与试题解析 ‎　‎ 一．解答题（共10小题）‎ ‎1．（2009•温州）某工厂用如图甲所示的长方形和正方形纸板，做成如图乙所示的竖式与横式两种长方体形状的无盖纸盒　　．‎ ‎（1）现有正方形纸板162张，长方形纸板340张．若要做两种纸盒共100个，设做竖式纸盒x个．‎ ‎①根据题意，完成以下表格：‎ 纸盒 纸板 竖式纸盒（个）‎ 横式纸盒（个）‎ ‎ x ‎100﹣x ‎ 正方形纸板（张）‎ ‎ 2（100﹣x）‎ ‎ 长方形纸板（张）‎ ‎ 4x ‎②按两种纸盒的生产个数来分，有哪几种生产方案？‎ ‎（2）若有正方形纸162张，长方形纸板a张，做成上述两种纸盒，纸板恰好用完．已知290＜a＜306．求a的值．‎ ‎【解答】解：（1）①如表：‎ 纸盒 纸板 竖式纸盒（个）‎ 横式纸盒（个）‎ x ‎100﹣x 正方形纸板（张）‎ x ‎2（100﹣x）‎ 长方形纸板（张）‎ ‎4x ‎3（100﹣x）‎ ‎②由题意得，，‎ 解得38≤x≤40．‎ 又∵x是整数，‎ ‎∴x=38，39，40．‎ 答：有三种方案：生产竖式纸盒38个，横式纸盒62个；‎ 生产竖式纸盒39个，横式纸盒61个；‎ 生产竖式纸盒40个，横式纸盒60个；‎ ‎（2）如果设x个竖式需要正方形纸板x张，长方形纸板横4x张；y个横式需要正方形纸板2y张，长方形纸板横3y张，可得方程组，‎ 于是我们可得出y=，‎ 因为已知了a的取值范围是290＜a＜306，‎ 所以68.4＜y＜71.6，由y取正整数，‎ 则，当取y=70，则a=298；‎ 当取y=69时，a=303；‎ 当取y=71时，a=293．‎ ‎293或298或303（写出其中一个即可）．‎ ‎　‎ ‎2．（2014•温州校级二模）有一种规格为165cm×30cm的标准板材，可按如图所示的两种裁法得到规格为60cm×30cm的A型板材与规格为35cm×30cm的B型板材．‎ ‎（1）某公司装修需要A型板材140张，B型板材215张．现购得标准板材100张，恰好裁完．设按裁法一裁剪的标准板材为x张．‎ ‎①根据题意，完成以下表格：‎ 标准板材裁法一 标准板材裁法二 ‎ x（张）‎ ‎　　（张）‎ A型板材（张）‎ ‎　　‎ ‎2（100﹣x）‎ B型板材（张）‎ ‎ 3x ‎　　‎ ‎②按以上两种裁法的张数来分，共有哪几种裁剪方案？‎ ‎（2）若装修师傅购买标准板材若干张，按以上两种方法裁剪后，得到A型板材恰为140张，B型板材恰为a张（180＜a＜200），则购进的标准板材可以是　93或94或95　张．（写出一个即可）‎ ‎【解答】解：（1）①‎ 标准板材裁法一（张）‎ 标准板材裁法二（张）‎ x ‎100﹣x A型板材（张）‎ x ‎2（100﹣x）‎ B型板材（张）‎ ‎3x ‎100﹣x ‎②由题意，得 解得57.5≤x≤60‎ 又∵x是整数 ‎∴x=58，59，60‎ 答：共有三种裁剪方案：按裁法一裁剪58张，按裁法二裁剪42张；按裁法一裁剪59张，按裁法二裁剪41张；按裁法一裁剪60张，按裁法二裁剪40张．‎ ‎（2）设标准板中有m张安裁法1裁剪，有n张安裁法2裁剪，根据题意得：‎ ‎，‎ 整理得：，‎ 解得44＜n＜48，由于n为正整数，则 n=45，46，47，‎ 则m=50，48，46，‎ 故标准板材为：95张，94张，93张．‎ ‎　‎ ‎3．（2014•温州二模）某校积极开展“促进有效学习”课堂教学改革实验，班内各个学习小组共设四个评价项目每月都要评奖：自主学习，课堂展示，互动点评，反馈检测，每个项目得分都按一定百分比折算后计入总分．下表为繁星、新月、初阳三个小组的得分情况（单位：分）‎ 自主学习 课堂展示 互动点评 反馈检测 繁星 ‎80‎ ‎50‎ ‎40‎ ‎70‎ 新月 ‎40‎ ‎80‎ ‎90‎ ‎35‎ 初阳 ‎40‎ ‎95‎ ‎85‎ ‎35‎ ‎（1）月底，繁星组组长猜测自主学习，课堂展示，互动点评，反馈检测这四项得分分别按10%，30%，20%，40%折算计入总分，根据猜测，求出繁星组的总分；‎ ‎（2）学校决定，总分为60分以上（包括60分）的学习小组获得优秀小组称号．现获悉新月、初阳两组的总分分别是64.5分，69.5分，繁星组的自主学习，反馈检测两项得分折算后的分数和是29分，问：繁星组能否获得优秀？‎ ‎【解答】解：（1）繁星小组总分为80×10%+50×30%+40×20%+70×40%=59．‎ ‎（2）设课堂展示所占百分比为x，活动点评所占百分比为y 由题意得，，‎ 解得 ，‎ 所以繁星组得分29+50×40%+40×20%=57＜60，‎ 所以繁星组不能获得优秀．‎ ‎　‎ ‎4．（2015•阳谷县一模）今年我区为绿化行车道，计划购买甲、乙两种树苗共计n棵．设买甲种树苗x棵．有关甲、乙两种树苗的信息如图所示．‎ ‎（1）当n=500时，‎ ‎①根据信息填表（用含x代数式表示）‎ 树苗类型 甲种树苗 乙种树苗 买树苗数量（单位：棵）‎ x 买树苗的总费用（单位：元）‎ ‎②如果购买甲、乙两种树苗共用25600元，那么甲、乙两种树苗各买了多少棵？‎ ‎（2）要使这批树苗的成活率不低于92%，且使购买这两种树苗的总费用为26000元，求n的最大值．‎ ‎【解答】解：①根据信息填表（用含x代数式表示） （每空格2分）‎ 树苗类型 甲种树苗 乙种树苗 买树苗数量 ‎（单位：棵）‎ ‎500﹣x 买树苗的总费用 ‎（单位：元）‎ ‎50x ‎80（500﹣x）‎ ‎②50x+80（500﹣x）=25600，‎ 解得x=480，‎ ‎500﹣x=20．‎ 答：甲种树苗买了480棵，乙种树苗买了20棵． ‎ ‎（2）90%x+95%（n﹣x）≥92%×n，‎ 解得x≤n ‎50x+80（n﹣x）=26000，‎ 解得x=，‎ ‎∴≤n，‎ ‎∴n≤419，‎ ‎∵n为正整数，x为正整数，‎ ‎∴n的最大值=419．‎ ‎　‎ ‎5．（2012•温州）温州享有“中国笔都”之称，其产品畅销全球，某制笔企业欲将n件产品运往A，B，C三地销售，要求运往C地的件数是运往A地件数的2倍，各地的运费如图所示．设安排x件产品运往A地．‎ ‎（1）当n=200时，①根据信息填表：‎ A地 B地 C地 合计 产品件数（件）‎ x ‎2x ‎200‎ 运费（元）‎ ‎30x ‎②若运往B地的件数不多于运往C地的件数，总运费不超过4000元，则有哪几种运输方案？‎ ‎（2）若总运费为5800元，求n的最小值．‎ ‎【解答】解：（1）①根据信息填表 A地 B地 C地 合计 产品件数（件）‎ ‎200﹣3x 运费 ‎1600﹣24x ‎50x ‎56x+1600‎ ‎②由题意，得，‎ 解得40≤x≤42，‎ ‎∵x为正整数，‎ ‎∴x=40或41或42，‎ ‎∴有三种方案，分别是（i）A地40件，B地80件，C地80件；‎ ‎ （ii）A地41件，B地77件，C地82件；‎ ‎ （iii）A地42件，B地74件，C地84件；‎ ‎（2）由题意，得30x+8（n﹣3x）+50x=5800，‎ 整理，得n=725﹣7x．‎ ‎∵n﹣3x≥0，‎ ‎∴725﹣7x﹣3x≥0，‎ ‎∴﹣10x≥﹣725，‎ ‎∴x≤72.5，‎ 又∵x≥0，‎ ‎∴0≤x≤72.5且x为正整数．‎ ‎∵n随x的增大而减少，‎ ‎∴当x=72时，n有最小值为221．‎ ‎　‎ ‎6．（2011•温州）2011年5月20日是第22个中国学生营养日，某校社会实践小组在这天开展活动，调查快餐营养情况．他们从食品安全监督部门获取了一份快餐的信息（如图）．根据信息，解答下列问题．‎ ‎（1）求这份快餐中所含脂肪质量；‎ ‎（2）若碳水化合物占快餐总质量的40%，求这份快餐所含蛋白质的质量；‎ ‎（3）若这份快餐中蛋白质和碳水化合物所占百分比的和不高于85%，求其中所含碳水化合物质量的最大值．‎ ‎【解答】解：（1）400×5%=20克．‎ 答：这份快餐中所含脂肪质量为20克；‎ ‎（2）设400克快餐所含矿物质的质量为x克，由题意得：‎ x+4x+20+400×40%=400，‎ ‎∴x=44，‎ ‎∴4x=176．‎ 答：所含蛋白质质量为176克；‎ ‎（3）设所含矿物质的质量为y克，则所含蛋白质质量为4y克，所含碳水化合物的质量为（380﹣5y）克．‎ ‎∴4y+（380﹣5y）≤400×85%，‎ ‎∴y≥40，‎ ‎∴﹣5y≤﹣200，‎ ‎∴380﹣5y≤380﹣200，‎ 即380﹣5y≤180，‎ ‎∴所含碳水化合物质量的最大值为180克．‎ ‎　‎ ‎7．（2014•温州一模）2013年1月，由于雾霾天气持续笼罩我国中东部大部分地区，口罩市场出现热卖，某旗舰网店用8000元购进甲、乙两种口罩，销售完后共获利2800元，进价和售价如下表：‎ ‎ 品名 价格 甲种口罩 乙种口罩 进价（元/袋）‎ ‎20‎ ‎25‎ 售价（元/袋）‎ ‎26‎ ‎35‎ ‎（1）求该网店购进甲、乙两种口罩各多少袋？‎ ‎（2）该网店第二次以原价购进甲、乙、两种口罩，购进乙种口罩袋数不变，而购进甲种口罩袋数是第一次的2倍．甲种口罩按原售价出售，而乙种口罩让利销售．若两种口罩销售完毕，要使第二次销售活动获利不少于3680元，乙种口罩最低售价为每袋多少元？‎ ‎【解答】解；（1）设网店购进甲种口罩x袋，乙种口罩y袋，‎ 根据题意得出：，‎ 解得：，‎ 答：甲种口罩200袋，乙种口罩160袋；‎ ‎（2）设乙种口罩每袋售价z元，根据题意得出：‎ ‎160（z﹣25）+2×200×（26﹣20）≥3680，‎ 解得：z≥33，‎ 答：乙种口罩每袋售价为每袋33元．‎ ‎　‎ ‎8．（2014•温州模拟）今年小芳家添置了新电器．已知今年5月份的用电量是240千瓦时．‎ ‎（1）若今年6月份用电量增长率是7月份用电量增长率的1.5倍，设今年7月份用电量增长率为x，‎ 补全下列表格内容（用含x代数式表示）‎ 月份 ‎6月份 ‎7月份 月增长率 x 用电量 ‎（单位：千瓦时）‎ ‎（2）在（1）的条件下，预计今年7月份的用电量将达到480千瓦时，求今年7月份用电量增长率x的值．（精确到1%）‎ ‎（3）若今年6月份用电量增长率是7月份用电量增长率的n倍，6月份用电量为360千瓦时，预计今年7月份的用电量将不低于500千瓦时．则n的最大值为　　．（直接写出答案）‎ ‎【解答】解：（1）‎ 月份 ‎6月份 ‎7月份 增长率 ‎1.5x x 用电量 ‎（单位：千瓦时）‎ ‎240（1+1.5x）‎ ‎240（1+x）（1+1.5x）‎ ‎（2）480=240（1+x）（1+1.5x），‎ 解得或x=﹣2（不合题意舍去），‎ ‎∴‎ ‎（3）设6月的增长率为x，列方程为240（1+x）=360，‎ 解得x=0.5，‎ 则7月的增长率为，列不等式360（1+）≥500，‎ 解得：n≤．∴n的最大值为，‎ ‎∴n的最大值为．‎ ‎　‎ ‎9．（2014•舟山）某汽车专卖店销售A，B两种型号的新能源汽车．上周售出1辆A型车和3辆B型车，销售额为96万元；本周已售出2辆A型车和1辆B型车，销售额为62万元．‎ ‎（1）求每辆A型车和B型车的售价各为多少元．‎ ‎（2）甲公司拟向该店购买A，B两种型号的新能源汽车共6辆，购车费不少于130万元，且不超过140万元．则有哪几种购车方案？‎ ‎【解答】解：（1）每辆A型车和B型车的售价分别是x万元、y万元．则 ‎，‎ 解得 ．‎ 答：每辆A型车的售价为18万元，每辆B型车的售价为26万元；‎ ‎（2）设购买A型车a辆，则购买B型车（6﹣a）辆，则依题意得 ‎，‎ 解得 2≤a≤3．‎ ‎∵a是正整数，‎ ‎∴a=2或a=3．‎ ‎∴共有两种方案：‎ 方案一：购买2辆A型车和4辆B型车；‎ 方案二：购买3辆A型车和3辆B型车．‎ ‎　‎ ‎10．（2012•湖州）为进一步建设秀美、宜居的生态环境，某村欲购买甲、乙、丙三种树美化村庄，已知甲、乙丙三种树的价格之比为2：2：3，甲种树每棵200元，现计划用210000元资金，购买这三种树共1000棵．‎ ‎（1）求乙、丙两种树每棵各多少元？‎ ‎（2）若购买甲种树的棵树是乙种树的2倍，恰好用完计划资金，求这三种树各能购买多少棵？‎ ‎（3）若又增加了10120元的购树款，在购买总棵树不变的前提下，求丙种树最多可以购买多少棵？‎ ‎【解答】解：（1）已知甲、乙丙三种树的价格之比为2：2：3，甲种树每棵200元，‎ 则乙种树每棵200元，‎ 丙种树每棵×200=300（元）；‎ ‎（2）设购买乙种树x棵，则购买甲种树2x棵，丙种树（1000﹣3x）棵．‎ 根据题意：‎ ‎200×2x+200x+300（1000﹣3x）=210000，‎ 解得x=300‎ ‎∴2x=600，1000﹣3x=100，‎ 答：能购买甲种树600棵，乙种树300棵，丙种树100棵；‎ ‎（3）设购买丙种树y棵，则甲、乙两种树共（1000﹣y）棵，‎ 根据题意得：‎ ‎200（1000﹣y）+300y≤210000+10120，‎ 解得：y≤201.2，‎ ‎∵y为正整数，‎ ‎∴y最大取201．‎ 答：丙种树最多可以购买201棵．‎ ‎　‎