2014四川省泸州市中考数学 12页

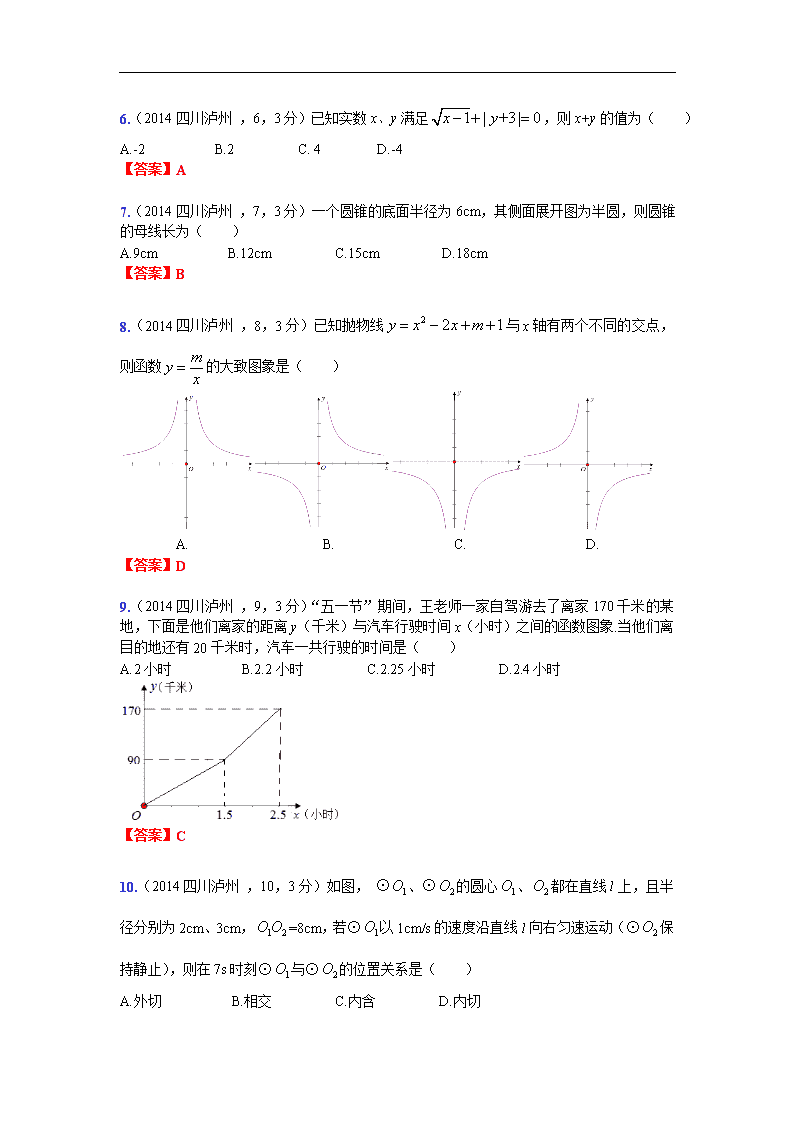
‎2014年四川省泸州市高中阶段学校招生考试 数 学 ‎（满分120分，考试时间120分钟）‎ 第一部分 选择题（共36分）‎ 一、选择题（本大题共12小题，每小题3分，满分36分，在每小题给出的四个选项中，只有一项是符合题目要求的。）‎ ‎1.（2014四川泸州 ，1，3分）5的倒数是（ ）‎ A. B.5 C. D.-5‎ ‎【答案】A ‎2.（2014四川泸州 ，2，3分）计算的结果为（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎3.（2014四川泸州 ，3，3分）如右下图所示的几何体的俯视图为（ ）‎ ‎【答案】C ‎4.（2014四川泸州 ，4，3分）某校八年级（2）班6名女同学的体重（单位：kg）分别为35,36,38,40,42,42，则这组数据的中位数是（ ）‎ A.38 B.39 C.40 D.42‎ ‎【答案】B ‎5.（2014四川泸州 ，5，3分）如图，等边△ABC中，点D、E分别为边AB、AC的中点，则∠DEC的度数为（ ）‎ A.30° B. 60° C.120° D.150°‎ ‎【答案】C ‎6.（2014四川泸州 ，6，3分）已知实数x、y满足，则x+y的值为（ ）‎ A.-2 B.2 C. 4 D.-4‎ ‎【答案】A ‎7.（2014四川泸州 ，7，3分）一个圆锥的底面半径为6cm，其侧面展开图为半圆，则圆锥的母线长为（ ）‎ A.9cm B.12cm C.15cm D.18cm ‎【答案】B ‎8.（2014四川泸州 ，8，3分）已知抛物线与x轴有两个不同的交点，则函数的大致图象是（ ）‎ A. B. C. 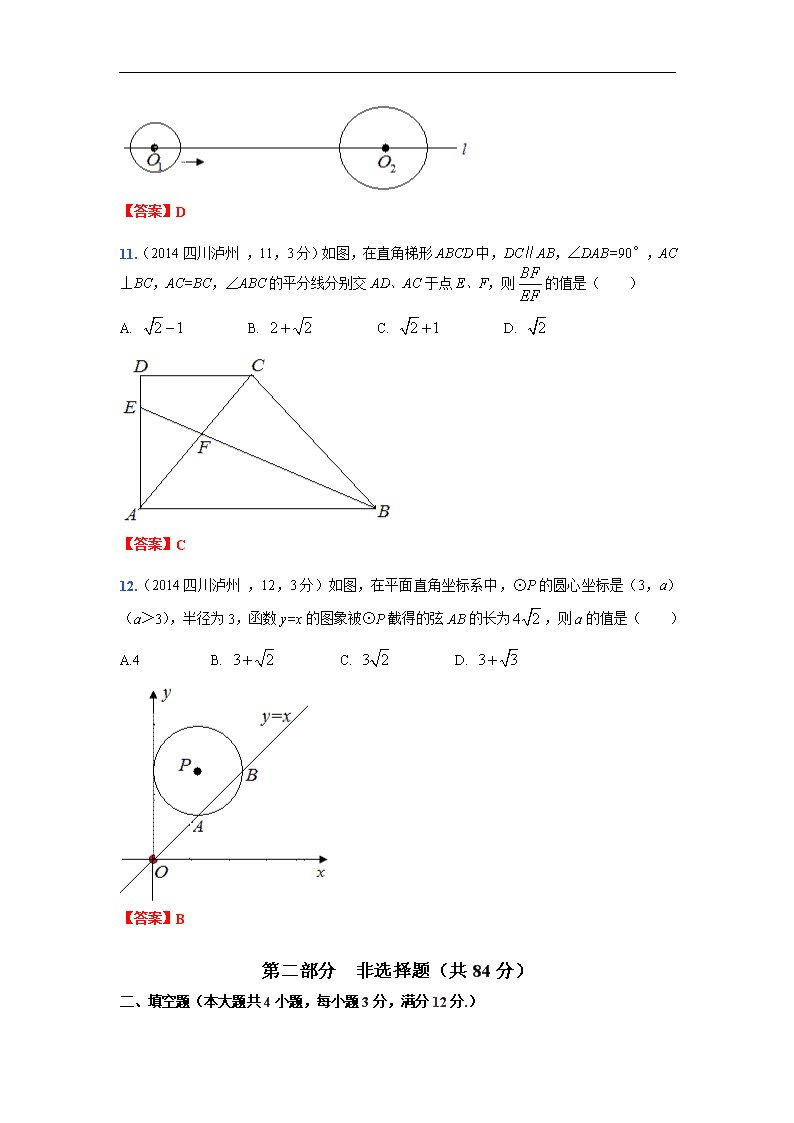D.‎ ‎【答案】D ‎9.（2014四川泸州 ，9，3分）“五一节”期间，王老师一家自驾游去了离家170千米的某地，下面是他们离家的距离y（千米）与汽车行驶时间x（小时）之间的函数图象.当他们离目的地还有20千米时，汽车一共行驶的时间是（ ）‎ A.2小时 B.2.2小时 C.2.25小时 D.2.4小时 ‎【答案】C ‎10.（2014四川泸州 ，10，3分）如图， ⊙、⊙的圆心、都在直线l上，且半径分别为2cm、3cm，=8cm，若⊙以1cm/s的速度沿直线l向右匀速运动（⊙保持静止），则在7s时刻⊙与⊙的位置关系是（ ）‎ A.外切 B.相交 C.内含 D.内切 ‎【答案】D ‎11.（2014四川泸州 ，11，3分）如图，在直角梯形ABCD中，DC∥AB，∠DAB=90°，AC⊥BC，AC=BC，∠ABC的平分线分别交AD、AC于点E、F，则的值是（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎12.（2014四川泸州 ，12，3分）如图，在平面直角坐标系中，⊙P的圆心坐标是（3，a）（a＞3），半径为3，函数y=x的图象被⊙P截得的弦AB的长为，则a的值是（ ）‎ A.4 B. C. D. ‎ ‎【答案】B 第二部分 非选择题（共84分）‎ 二、填空题（本大题共4小题，每小题3分，满分12分.）‎ ‎13.（2014四川泸州 ，13，3分）分解因式：= .‎ ‎【答案】‎ ‎14.（2014四川泸州 ，14，3分）使函数有意义的自变量x的取值范围是 .‎ ‎【答案】x＞-2且x≠1‎ ‎15.（2014四川泸州 ，15，3分）一个平行四边形的一条边长为3，两条对角线的长分别为4和，则它的面积为 .‎ ‎【答案】‎ ‎16.（2014四川泸州 ，16，3分）如图，矩形AOBC的顶点坐标分别为A（0,3），O（0,0），B（4,0），C（4,3），动点F在边BC上（不与B、C重合），过点F的反比例函数的图象与边AC交于点E，直线EF分别与y轴和x轴交于点D和G.给出下列命题：①若k=4，则△OEF的面积为；②若k=，则点C关于直线EF的对称点在x轴上；③满足题设的k的取值范围是0＜k≤12；④若，则k=1.其中正确的命题的序号是 .（写出所有正确命题的序号）‎ ‎【答案】④‎ 三、（本大题共3个小题，每小题6分，共18分）‎ ‎17.（2014四川泸州 ，17，6分）计算：.‎ ‎【答案】解：=‎ ‎==1+4=5.‎ ‎18.（2014四川泸州 ，18，6分）化简：‎ ‎【答案】解：=‎ ‎===‎ ‎==.‎ ‎19.（2014四川泸州 ，19，6分）如图正方形ABCD中，E、F分别为BC、CD上的点，且AE⊥BF，垂足为G，求证：AE=BF.‎ ‎【答案】证明：∵四边形ABCD是正方形，‎ ‎∴AB=BC，∠ABC=∠BCF=90°，∴∠BAE+∠AEB=90°.‎ 又∵AE⊥BF，垂足为G，∴∠CBF+∠AEB=90°.‎ ‎∴∠BAE=∠CBF.‎ 在△ABE与△BCF中 ‎，‎ ‎∴△ABE≌△BCF（ASA），‎ ‎∴AE=BF.‎ 四、（本大题共2个小题，每小题7分，共14分）‎ ‎20.（2014四川泸州 ，20，7分）某中学积极组织学生开展课外阅读活动.为了了解本校学生每周课外阅读的时间量t（单位：小时），采用随机抽样的方法抽取部分学生进行问卷调查，调查的结果按0≤t＜2，2≤t＜3，3≤t＜4， t≥4分为四个等级，并分别用A、B、C、D表示，根据调查结果统计数据绘制成了如图所示的两幅不完整的统计图.由图中给出的信息解答下列问题：‎ ‎ ‎ ‎(1)求出x的值，并将不完整的条形统计图补充完整；‎ ‎(2)若该校共有学生2500人，试估计每周课外阅读时间量满足2≤t＜4的人数；‎ ‎(3)‎ 在本次调查活动中，九年级（1）班的两个学习小组分别有3人和2人每周阅读时间量都在4小时以上，现从这5人中任选2人参加学校组织的知识抢答赛，求选出的2人来自不同小组的概率.‎ ‎【答案】解：(1)∵x%=1-45%-10%-15%=30%，‎ ‎∴x=30.‎ ‎∵90÷45%=200，‎ ‎∴B、C的人数分别为：200×30%=60，200×10%=20.‎ 补全统计图如下：‎ ‎(2)每周课外阅读时间量满足2≤t＜4的人数为：2500×（30%+10%）=2500×40%=1000.‎ ‎(3)画树状图如下：‎ ‎∴P(2人来自不同小组)= .‎ ‎21.（2014四川泸州 ，21，7分）某工厂现有甲种原料380千克，乙种原料290千克，计划用这两种原料生产A、B两种产品共50件.已知生产1件A种产品需甲种原料9千克，乙种原料3千克，可获利700元；生产1件B种产品需甲种原料4千克，乙种原料10千克，可获利1200元.设生产A、B两种产品可获总利润是y元，其中A种产品的生产件数是x.‎ ‎(1)写出y与x之间的函数关系式；‎ ‎(2)如何安排A、B两种产品的生产件数，使总利润y有最大值，并求出y的最大值.‎ ‎【答案】解：(1)∵A种产品的生产件数是x，∴B种产品的生产件数是50-x，由题意得 y=700x+1200(50-x)= -500x+60000.‎ ‎(2)由题意得，解得30≤x≤36.‎ 在y= -500x+60000中，‎ ‎∵-500＜0，‎ ‎∴当x=30时，总利润y有最大值， y的最大值为：‎ ‎-500×30+60000=-15000+60000=45000(元).‎ 五、（本大题共2个小题，每小题8分，共16分）‎ ‎22.（2014四川泸州 ，22，8分）海中有两个灯塔A、B，其中B位于A的正东方向上，渔船跟踪鱼群由西向东航行，在点C处测得灯塔A在西北方向上，灯塔B在北偏东30°方向上，渔船不改变航向继续向东航行30海里到达点D，这时测得灯塔A在北偏西60°方向上，求灯塔A、B间的距离.(计算结果用根号表示，不取近似值)‎ ‎ ‎ ‎【答案】解：作CE⊥AB于点E，AF⊥CD于点F，‎ ‎∴∠AFC=∠AEC =90°.‎ ‎∵∠FCE=90°，∠ACE=45°，‎ ‎∴四边形AFCE是正方形.‎ 设AF=FC=CE=AE=x，则FD=x+30，‎ ‎∵，∠AFD=90°，∠D=30°，‎ ‎∴，解得x=，‎ ‎∴AE=CE=.‎ ‎∵，∠CEB=90°，∠BCE=30°，‎ ‎∴，解得BE=.‎ ‎∴AB=AE+BE=+=.‎ ‎23.（2014四川泸州 ，23，8分）已知、是关于x的一元二次方程的两个实数根.‎ ‎(1)若，求m的值；‎ ‎(2)已知等腰△ABC的一边长为7，若、恰好是△ABC另外两边的边长，求这个三角形的周长.‎ ‎【答案】解：(1)∵、是关于x的一元二次方程 的两个实数根，∴，‎ 又∵，‎ ‎∴‎ ‎=28，‎ 即，∴m=-4或6.‎ 又∵△‎ ‎＞0，∴m＞2，‎ ‎∴m=6.‎ ‎(2)∵m=6，‎ ‎∴，‎ ‎∴三角形的周长为7+14=21.‎ 五、（本大题共2个小题，每小题12分，共24分）‎ ‎24.（2014四川泸州 ，24，12分）如图，四边形ABCD内接于⊙O，AB是⊙O直径，AC和BD相交于点E，且.‎ ‎(1)求证：BC=CD；‎ ‎(2)分别延长AB、DC交于点P，过A点作AF⊥CD交CD的延长线于点F. 若PB=OB，CD= ，求DF的长.‎ ‎【答案】解：(1)∵，‎ ‎∴.‎ 又∵∠DCE=∠ACD，‎ ‎∴△DCE∽△ACD，‎ ‎∴∠CDE=∠CAD，‎ ‎∴BC=CD.‎ ‎(2)连接OC，作OG⊥CD于点G，‎ 则DG=CG=CD=.‎ ‎∵OG⊥CD，AF⊥CD，‎ ‎∴OG∥AF，‎ ‎∴.‎ ‎∵BC=CD，‎ ‎∴OC⊥BD.‎ ‎∵AB是⊙O直径，‎ ‎∴∠ADB=90°，‎ ‎∴AD⊥BD.‎ ‎∴OC∥AD，‎ ‎∴‎ 又∵PB=OB=OA，CD=，‎ ‎∴，‎ ‎∴CP=.‎ ‎∴，‎ ‎∴DF=.‎ ‎25.（2014四川泸州 ，25，12分）如图，已知一次函数的图象l与二次函数的图象C’都经过点B（0,1）和点C，且图象C’过点A（，0）.‎ ‎（1）求二次函数的最大值；‎ ‎（2）设使＞成立的x取值的所有整数和为s，若s是关于x的方程 的根，求a的值；‎ ‎（3）若点F、G在图象C’上，长度为的线段DE在线段BC上移动，EF与DG都始终平行于y轴，当四边形DEFG的面积最大时，在x轴上求一点P，使PD+PE最小，求出点P的坐标.‎ ‎【答案】解：(1)∵一次函数的图象l与二次函数的图象C’都经过点B（0,1）和点C，‎ ‎∴b=1，∴一次函数解析式为.‎ 又∵且图象C’过点A（，0），‎ ‎∴‎ 解得m=4，‎ ‎∴二次函数的解析式为：，‎ ‎∴二次函数的最大值为：‎ ‎===5.‎ ‎(2)由，解得（舍去）.‎ 结合图象可知：若＞成立的x取值的所有整数为1、2、3，‎ ‎∴它们的和为s=1+2+3=6.‎ 又∵s是关于x的方程的根，‎ ‎∴，‎ 解得a=.‎ ‎（3）设点D（x，），则点G、E、F的坐标分别为G(x，)， E(x+2，)， F(x+2，)，梯形的高为2，‎ ‎∴四边形DEFG的面积为：‎ ‎，‎ ‎∴当时，面积最大，‎ 此时点D、E的坐标分别为（，），（，）.‎ ‎∴点D关于x轴的对称点为D’（，），‎ 设DD’交x轴于点M，连接D’E交x轴于点P（x，0），此时PD+PE最小.‎ 作EN⊥GD于点N，则EN∥PM，∴.‎ 由题意得，，，EN=2，‎ ‎∴，解得.‎ ‎∴点P的坐标为（，0）.‎