中考数学模拟测试 16页

‎2013年模拟初三数学试卷36‎ 一、选择题：（3*10＝30分）‎ ‎1．-6的倒数是（　　　　）‎ A．6 B． C． D．‎ ‎2．PM2.5是大气中粒径小于等于2.5微米的颗粒物，称为细颗粒物，是表征环境空气质量的主要污染物指标．2.5微米等于‎0.0000025米，把0.0000025用科学记数法表示为（　　　　）‎ ‎ A． B． C． D．‎‎ ‎ 主视图 左视图 俯视图 ‎3．右图所示的是一个几何体的三视图，则这个几何体是（　　　　）‎ A．球 B．圆锥 C．圆柱 D．三棱柱 ‎4．已知一个多边形的内角和是外角和的3倍，则这个多边形的边数是（　　　　）‎ A．8 B．‎6 ‎ C．5 D．3‎ ‎5．在一个不透明的口袋中，装有5个红球3个白球，它们除颜色外都相同，从中任意摸出一个球，摸到红球的概率为（　　　　）‎ A． B． C． D．‎ ‎6．已知圆锥侧面展开图的扇形半径为‎2cm，面积是，则扇形的弧长和圆心角的度数分别为（　　　　）‎ A． B． C． D．‎ ‎7．甲、乙两人进行射击比赛，他们5次射击的成绩（单位：环）如下表所示： ‎ 甲 ‎7‎ ‎9‎ ‎8‎ ‎6‎ ‎10‎ 乙 ‎7‎ ‎8‎ ‎9‎ ‎8‎ ‎8‎ 设甲、乙两人射击成绩的平均数依次为、，射击成绩的方差依次为、，则下列判断中正确的是（　　　　）‎ A．， B．， ‎ C．， D．， ‎ ‎8．如图，在平行四边形ABCD中，AC = 12，BD = 8，P是 AC上的一个动点，过点P作EF∥BD，与平行四边形的 两条边分别交于点E、F．设CP=x，EF=y，则下列图象 中，能表示y与x的函数关系的图象大致是（　　　　）‎ ‎ A． B． C． D．‎ ‎9.在平面直角坐标系中，对于平面内任意一点(x，y)，若规定以下两种变换：‎ ‎①f(x，y) = (y，x)：如f(2，3) = (3，2)；②g(x，y) = (-x，-y)：如g(2，3) =(-2，-3)．按照以上变换有：f(g(2，3)) =f(-2，-3) =(-3，-2)，那么g(f(-6，7)) =（ ）‎ A．(7，6) B．(7，-6) C．(-7，6) D．(-7，-6)‎ D C B E A H ‎10.在直角梯形中，，为边上一点，，且．连接交对角线于，连接．下列结论：①；②为等边三角形；③；④ ．其中结论正确的是（　　　　）‎ A．①② B．①②④ C．③④ D．①②③④‎ 二、填空题：（3*5＝15分）‎ ‎11．分解因式： ．‎ A B C D E F M N ‎12．在函数中，自变量的取值范围是 ．‎ ‎13．计算：＝　　　　　　　　　．‎ ‎14．如图，将边长为2的正方形纸片ABCD折叠，使点B ‎ 落在CD上，落点记为E（不与点C，D重合），点A 落在点F处，折痕MN交AD于点M，交BC于点N．‎ 若，则BN的长是 ，的值 等于 ；若（，且为整数）， ‎ 则的值等于 （用含的式子表示）．‎ ‎15．如图，已知Rt△ABC≌Rt△DEF，∠C=∠F=90°，AC=DF=3，BC=EF=4，△DEF绕着斜边AB的中点D旋转，‎ DE，DF分别交AC，BC所在的直线于点P，Q．‎ 当△BDQ为等腰三角形时，AP的长为___________． ‎ 三、解答题：（5+5+6+7+7+7+8+8+10+12＝75分）‎ ‎16. （5分）已知，求的值.‎ ‎17. （5分）解不等式组并把解集在数轴上表示出来.‎ ‎2013年模拟初三数学试卷36‎ 一、选择题：（3*10＝30分）‎ ‎1．-6的倒数是（　　　　）‎ A．6 B． C． D．‎ ‎2．PM2.5是大气中粒径小于等于2.5微米的颗粒物，称为细颗粒物，是表征环境空气质量的主要污染物指标．2.5微米等于‎0.0000025米，把0.0000025用科学记数法表示为（　　　　）‎ ‎ A． B． C． D．‎‎ ‎ 主视图 左视图 俯视图 ‎3．右图所示的是一个几何体的三视图，则这个几何体是（　　　　）‎ A．球 B．圆锥 C．圆柱 D．三棱柱 ‎4．已知一个多边形的内角和是外角和的3倍，则这个多边形的边数是（　　　　）‎ A．8 B．‎6 ‎ C．5 D．3‎ ‎5．在一个不透明的口袋中，装有5个红球3个白球，它们除颜色外都相同，从中任意摸出一个球，摸到红球的概率为（　　　　）‎ A． B． C． D．‎ ‎6．已知圆锥侧面展开图的扇形半径为‎2cm，面积是，则扇形的弧长和圆心角的度数分别为（　　　　）‎ A． B． C． D．‎ ‎7．甲、乙两人进行射击比赛，他们5次射击的成绩（单位：环）如下表所示： ‎ 甲 ‎7‎ ‎9‎ ‎8‎ ‎6‎ ‎10‎ 乙 ‎7‎ ‎8‎ ‎9‎ ‎8‎ ‎8‎ 设甲、乙两人射击成绩的平均数依次为、，射击成绩的方差依次为、，则下列判断中正确的是（　　　　）‎ A．， B．， ‎ C．， D．， ‎ ‎8．如图，在平行四边形ABCD中，AC = 12，BD = 8，P是 AC上的一个动点，过点P作EF∥BD，与平行四边形的 两条边分别交于点E、F．设CP=x，EF=y，则下列图象 中，能表示y与x的函数关系的图象大致是（　　　　）‎ ‎ A． B． C． D．‎ ‎9.在平面直角坐标系中，对于平面内任意一点(x，y)，若规定以下两种变换：‎ ‎①f(x，y) = (y，x)：如f(2，3) = (3，2)；②g(x，y) = (-x，-y)：如g(2，3) =(-2，-3)．按照以上变换有：f(g(2，3)) =f(-2，-3) =(-3，-2)，那么g(f(-6，7)) =（ ）‎ A．(7，6) B．(7，-6) C．(-7，6) D．(-7，-6)‎ D C B E A H ‎10.在直角梯形中，，为边上一点，，且．连接交对角线于，连接．下列结论：①；②为等边三角形；③；④ ．其中结论正确的是（　　　　）‎ A．①② B．①②④ C．③④ D．①②③④‎ 二、填空题：（3*5＝15分）‎ ‎11．分解因式： ．‎ A B C D E F M N ‎12．在函数中，自变量的取值范围是 ．‎ ‎13．计算：＝　　　　　　　　　．‎ ‎14．如图，将边长为2的正方形纸片ABCD折叠，使点B ‎ 落在CD上，落点记为E（不与点C，D重合），点A 落在点F处，折痕MN交AD于点M，交BC于点N．‎ 若，则BN的长是 ，的值 等于 ；若（，且为整数）， ‎ 则的值等于 （用含的式子表示）．‎ ‎15．如图，已知Rt△ABC≌Rt△DEF，∠C=∠F=90°，AC=DF=3，BC=EF=4，△DEF绕着斜边AB的中点D旋转，‎ DE，DF分别交AC，BC所在的直线于点P，Q．‎ 当△BDQ为等腰三角形时，AP的长为___________． ‎ 三、解答题：（5+5+6+7+7+7+8+8+10+12＝75分）‎ ‎16. （5分）已知，求的值.‎ ‎17. 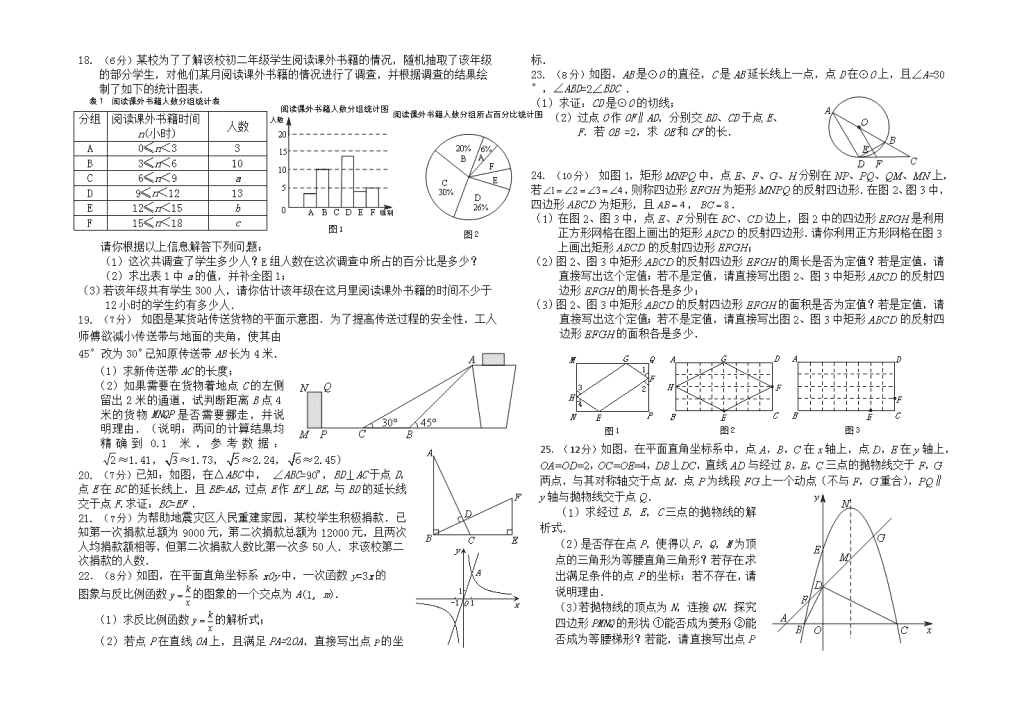（5分）解不等式组并把解集在数轴上表示出来.‎ 表1 阅读课外书籍人数分组统计表 ‎18. （6分）某校为了了解该校初二年级学生阅读课外书籍的情况，随机抽取了该年级的部分学生，对他们某月阅读课外书籍的情况进行了调查，并根据调查的结果绘制了如下的统计图表． ‎ 分组 阅读课外书籍时间n(小时)‎ 人数 A ‎0≤n＜3‎ ‎3‎ B ‎3≤n＜6‎ ‎10‎ C ‎6≤n＜9‎ a D ‎9≤n＜12‎ ‎13‎ E ‎12≤n＜15‎ b F ‎15≤n＜18‎ c 阅读课外书籍人数分组所占百分比统计图 图2‎ 阅读课外书籍人数分组统计图 图1‎ 请你根据以上信息解答下列问题：‎ （1） 这次共调查了学生多少人？E组人数在这次调查中所占的百分比是多少？ ‎ （2） 求出表1中a的值，并补全图1；‎ （3） 若该年级共有学生300人，请你估计该年级在这月里阅读课外书籍的时间不少于12小时的学生约有多少人．‎ ‎19. （7分） 如图是某货站传送货物的平面示意图．为了提高传送过程的安全性，工人师傅欲减小传送带与地面的夹角，使其由45°改为30°．已知原传送带AB长为4米．‎ ‎（1）求新传送带AC的长度；‎ ‎（2）如果需要在货物着地点C的左侧留出2米的通道，试判断距离B点4米的货物MNQP是否需要挪走，并说明理由．（说明：两问的计算结果均精确到0.1米，参考数据：≈1.41，≈1.73，≈2.24，≈2.45）‎ ‎20. （7分）已知：如图，在△ABC中， ∠ABC=90º，BD⊥AC于点D，点E在BC的延长线上，且BE=AB，过点E作EF⊥BE，与BD的延长线交于点F.求证：BC=EF . ‎ x ‎-1‎ ‎1‎ ‎1‎ O y A ‎21. （7分）为帮助地震灾区人民重建家园，某校学生积极捐款．已知第一次捐款总额为9000元，第二次捐款总额为12000元，且两次人均捐款额相等，但第二次捐款人数比第一次多50人．求该校第二次捐款的人数．‎ ‎22．（8分）如图，在平面直角坐标系xOy中，一次函数y=3x的 图象与反比例函数的图象的一个交点为A(1, m)．‎ ‎（1）求反比例函数的解析式；‎ ‎（2）若点P在直线OA上，且满足PA=2OA，直接写出点的坐标．‎ ‎23. （8分）如图，AB是⊙O的直径，C是AB延长线上一点，点D在⊙O上，且∠A=30°，∠ABD=2∠BDC ． ‎ ‎（1）求证：CD是⊙O的切线；‎ ‎（2）过点O作OF∥AD，分别交BD、CD于点E、‎ F．若OB =2，求 OE和CF的长．‎ ‎24. （10分） 如图1，矩形MNPQ中，点E、F、G、H分别在NP、PQ、QM、MN上，若，则称四边形EFGH为矩形MNPQ的反射四边形．在图2、图3中，四边形ABCD为矩形，且，．‎ ‎（1）在图2、图3中，点E、F分别在BC、CD边上，图2中的四边形EFGH是利用正方形网格在图上画出的矩形ABCD的反射四边形．请你利用正方形网格在图3上画出矩形ABCD的反射四边形EFGH；‎ ‎（2）图2、图3中矩形ABCD的反射四边形EFGH的周长是否为定值？若是定值，请直接写出这个定值；若不是定值，请直接写出图2、图3中矩形ABCD的反射四边形EFGH的周长各是多少；‎ ‎（3）图2、图3中矩形ABCD的反射四边形EFGH的面积是否为定值？若是定值，请直接写出这个定值；若不是定值，请直接写出图2、图3中矩形ABCD的反射四边形EFGH的面积各是多少．‎ A B C D E F 图3‎ M N P Q G H E F ‎1‎ ‎2‎ ‎3‎ ‎4‎ 图1‎ 图2‎ G A B C D E F H ‎25. （12分）如图，在平面直角坐标系中，点A，B，C在x轴上，点D，E在y轴上，OA=OD=2，OC=OE=4，DB⊥DC，直线AD与经过B，E，C三点的抛物线交于F，G两点，与其对称轴交于点M．点P为线段FG上一个动点（不与F，G重合），PQ∥y轴与抛物线交于点Q．‎ ‎（1）求经过B，E，C三点的抛物线的解析式．‎ ‎（2）是否存在点P，使得以P，Q，M为顶点的三角形为等腰直角三角形？若存在，求出满足条件的点P的坐标；若不存在，请说明理由．‎ ‎（3）若抛物线的顶点为N，连接QN，探究四边形PMNQ的形状：①能否成为菱形；②能否成为等腰梯形？若能，请直接写出点P 的坐标；若不能，请说明理由．‎ ‎2.下列图形中，既是轴对称图形又是中心对称图形的共有（ ）‎ A．1个 B．2个 C．3个 D．4个 ‎3.某种微粒子，测得它的质量为0.000 067 46克，这个质量用科学记数法表示（保留三个有效数字）应为（ ）‎ A．6.75×10-5克 B．6.74×10-5克 C．6.74×10-6克 D．6.75×10-6克 ‎5.某市5月上旬前五天的最高气温如下（单位：°C）：28，29，31，29，33，对这组数据，下列说法错误的是（ ）‎ A．平均数是30 B．众数是29 C．中位数是31 D．极差是5‎ ‎9.如图，直角梯形AOCD的边OC在x轴上，O为坐标原点，CD垂直于x轴，点D的坐标为(5，4)，AD=2．若动点E，F同时从点O出发，点E沿折线OA-AD-DC运动，到达C点时停止；点F沿OC运动，到达C点时停止，它们运动的速度都是每秒1个单位长度．设点E运动x秒时，△EOF的面积为y（平方单位），则y关于x的函数图象大致为（ ）‎ A． B． C． D．‎ 化简：_________．‎ 某市初中毕业男生体育测试项目有四项，其中“立定跳远”、“1000米跑”、“掷实心球”为必测项目，另一项从“篮球运动”或“一分钟跳绳”中选一项测试．小亮、小明和大刚从“篮球运动”或“一分钟跳绳”中选择同一个测试项目的概率是__________．‎ 已知：在△ABC中，AC=a，AB与BC所在直线成45°角，AC与BC所在直线形成的夹角的余弦值为（即cosC=），则AC边上的中线长是 ‎____________．‎ 如图，已知Rt△ABC≌Rt△DEF，∠C=∠F=90°，AC=DF=3，BC=EF=4，△DEF绕着斜边AB的中点D旋转，DE，DF分别交AC，BC所在的直线于点P，Q．当△BDQ为等腰三角形时，AP的长为___________．‎ 二、填空题（本题共16分，每小题4分）‎ 三、解答题（本题共30分，每小题5分）‎ ‎13．计算：．‎ ‎14．已知关于x的一元二次方程有两个相等的实数根，求m的值及方程的根．‎ ‎15．已知，求的值. ‎ ‎16． ‎ ‎17． ‎ ‎18．列方程或方程组解应用题： ‎ 四、解答题（本题共20分，每小题5分） ‎ ‎19．如图，在四边形ABCD中，∠DAB=60º，AC平分 ‎∠DAB，BC⊥AC，AC与BD交于点E，AD=6，‎ CE=，，求BC、DE的长及 四边形ABCD的面积．‎ ‎20． ‎ ‎21． ‎ ‎22． ‎ ‎ ‎ 五、解答题（本题共22分，第23题7分，第24题7分，第25题8分） ‎ ‎23． 在平面直角坐标系xOy中，抛物线经过原点O， ‎ 点B(-2,n)在这条抛物线上.‎ ‎（1）求抛物线的解析式；‎ ‎（2）将直线沿y轴向下平移b个单位后得到直线l， 若直线l经过B点，求n、b的值；‎ x y ‎1‎ ‎1‎ O ‎（3）在（2）的条件下，设抛物线的对称轴与x轴交于点C，直线l与y轴交于点D，且与抛物线的对称轴交于点E.若P是抛物线上一点，且PB=PE，求P点的坐标.‎ ‎24．已知：在△AOB与△COD中，OA＝OB，OC＝OD，． ‎ ‎（1）如图1，点C、D分别在边OA、OB上，连结AD、BC，点M为线段BC的中点，连结OM，则线段AD与OM之间的数量关系是 ，位置关系是 ；‎ ‎（2）如图2，将图1中的△COD绕点逆时针旋转，旋转角为 ()．连结AD、BC，点M为线段BC的中点，连结OM．请你判断（1）中的两个结论是否仍然成立．若成立，请证明；若不成立，请说明理由；‎ ‎（3）如图3，将图1中的 △COD绕点 O逆时针旋转到使 △COD的一边OD恰好与 ‎△AOB的边OA在同一条直线上时，点C落在OB上，点M为线段BC的中点．‎ 请你判断（1）中线段AD与OM之间的数量关系是否发生变化，写出你的猜想，并加以证明．‎ ‎25． 如图，在平面直角坐标系xOy中， 已知矩形ABCD的两个顶点B、C的坐标分别是B（1，0）、C（3，0）．直线AC与y轴交于点G（0，6）．动点P从点A出发，沿线段AB向点B运动．同时动点 Q从点C出发，沿线段CD向点D运动．点P、Q的运动速度均为每秒1个单位，运动时间为t秒．过点P作PE⊥AB交AC于点E．‎ ‎（1）求直线AC的解析式；‎ ‎（2）当t为何值时，△CQE的面积最大？最大值为多少？‎ ‎（3）在动点P、Q运动的过程中，当t为何值时，在矩形ABCD内（包括边界）存在点H，使得以C、Q、E、H为顶点的四边形是菱形？ ‎ ‎10. 已知两直线、为正整数），设这两条直线与轴所围成的三角形的面积为，则的值是（ ）‎ ‎ A． B． C． D．‎ 如图，把一块直角三角板的直角顶点放在直尺的一边上，如果∠1=32o，那么∠2的度数是（ ）‎ A.32o B.58o C.68o D.60o ‎ ‎7． ‎ ‎4．若与|x－y－3|互为相反数，则x＋y的值为(　　)‎ A．3 B．‎9 ‎‎ C．12 D．27‎ ‎５．下列图形中，既是轴对称图形，又是中心对称图形的是（ 　　 ）‎ ‎7. .下列计算正确的是（ ）‎ A a＋‎2a＝‎3a2 Ba·a2＝a3 ‎ C （‎2a）2＝‎2a2 D（－a2）3＝a6‎ ‎14. 一个圆锥的母线长为4，侧面积为8，则这个圆锥的底面圆的半径是 ．‎ 如图，某一中学生耐力测试比赛中，甲、乙两学生测试的路程s（米）与时间t（秒）之间的函数关系的图象分别为折线OABC和线段OD，下列说法正确的是（ ）．科 A．乙比甲先到终点科网 B．乙测试的速度随时间增加而增大学科网 C．比赛进行到29.4秒时，两人出发后第一次相遇科网 D．比赛全程甲的测试速度始终比乙的测试速度快学科网 ‎‎ ‎【答案】解：（1）∵点A（1，4）在函数y＝的图像上，‎ ‎∴4＝，得m＝4.……………………………2分 ‎（2）∵点B（a，b）在函数y＝的图像上，∴ab＝4.‎ 又∵AC⊥x轴于C，BD⊥y轴于D交AC于M，∴AC⊥BD于M ‎∴M（1，b），D（0，b），C（1，0）‎ ‎∴tan∠BAC＝＝＝＝，tan∠DCM＝＝……………4分 ‎∴tan∠BAC ＝tan∠DCM，‎ 所以锐角∠BAC＝∠DCM，DC∥AB………………………………………………6分 说明：利用两边对应成比例且夹角相等的三角形相似，易证△ABM∽△CDM，易得∠BAC＝∠DCM.评分标准为证出相似得到4分，证出平行得到6分.‎ ‎（3）设直线AB的解析式为y＝kx＋b ‎∵AB∥CD，AD＝BC，∴四边形ABCD是平行四边形或等腰梯形.‎ ① 四边形ABCD是平行四边形时，AC与BD互相平分，‎ 又∵AC⊥BD，∴B（2，2）‎ ‎∴，解得 ‎∴直线AB的解析式为：y＝－2x＋6.………………8分 ‎②当四边形ABCD是等腰梯形时，‎ BD与AC相等且垂直，∵AC＝BD＝4，‎ ‎∴B（4，1）‎ ‎∴同理可求直线AB的解析式为y＝－x＋5.…………………10分 ‎23.(本题12分)‎ 解：（1）∵抛物线y=ax2+bx+6经过点A（-3，0）和点B（2，0），‎ ‎9a‎-3b+6=0‎ ‎4a‎+2b+6=0‎ 解得：‎ a=-1‎ b=-1‎ ‎∴抛物线的解析式为y=-x2-x+6．------------------4分 ‎（2）∵把x=0代入y=-x2-x+6，得y=6．‎ ‎∴点C的坐标为（0，6）．‎ 设经过点B和点C的直线的解析式为y=mx+n，则 ‎2m‎+n=0‎ n=6‎ 解得 m=-3‎ n=6‎ ‎∴经过点B和点C的直线的解析式为：y=-3x+6．‎ ‎∵点E在直线y=h上，‎ ‎∴点E的坐标为（0，h）．‎ ‎∴OE=h．‎ ‎∵点D在直线y=h上，‎ ‎∴点D的纵坐标为h．‎ 把y=h代入y=-3x+6，得h=-3x+6．‎ 解得x=‎ ‎∴点D的坐标为（，h）．‎ ‎∴DE=‎ ‎∴S△BDE= h ‎∴当h=3时，△BDE的面积最大，最大面积是------------------4分 ‎（3）存在符合题意的直线y=h．‎ 设经过点A和点C的直线的解析式为y=kx+p，则 ‎-3k+p=0,p=6解得 k=2,p=6,故经过点A和点C的直线的解析式为y=2x+6．‎ 把y=h代入y=2x+6，得h=2x+6．‎ 解得x=．‎ ‎∴点F的坐标为（，h）．‎ ‎①若OF=OM，则整理，得5h2-12h+20=0．‎ ‎∵△=（-12）2-4×5×20=-256＜0，‎ ‎∴此方程无解．‎ ‎∴OF=OM不成立．‎ ‎②若OF=MF，则解得h=4．‎ 把y=h=4代入y=-x2-x+6，得-x2-x+6=4，‎ 解得x1=-2，x2=1．‎ ‎∵点G在第二象限，‎ ‎∴点G的坐标为（-2，4）．‎ ‎③若MF=OM，则解得h1=2，h2=-（不合题意，舍去）．‎ 把y=h1=2代入y=-x2-x+6，得-x2-x+6=2．‎ 解得x1=，x2=‎ ‎∵点G在第二象限，‎ ‎∴点G的坐标为（，2）．‎ 综上所述，存在这样的直线y=2或y=4，使△OMF是等腰三角形，当h=4时，点G的坐标为（-2，4）；当h=2时，点G的坐标为（，2）．------------------4分 如图，已知Rt△ABC≌Rt△DEF，∠C=∠F=90°，AC=DF=3，BC=EF=4，△DEF绕着斜边AB的中点D旋转，DE、DF分别交AC、BC所在的直线于点P，Q．当△BDQ为等腰三角形时，AP的长为 ‎25‎ ‎6‎ 或 ‎13‎ ‎6‎ 或 ‎11‎ ‎12‎ ‎．‎ 解 析解：（1）当BD=BQ， ∠C=∠F=90°，AC=DF=3，BC=EF=4，则AB=5， 过D作DM⊥BC与M，DN⊥AC于N，如图， ∵D为AB的中点， ∴DM=AN=‎ ‎1‎ ‎2‎ AC=‎ ‎3‎ ‎2‎ ‎，BD=‎ ‎1‎ ‎2‎ AB=‎ ‎5‎ ‎2‎ ‎，DN=BM=‎ ‎1‎ ‎2‎ AC=2， ∴BQ=BD=‎ ‎5‎ ‎2‎ ‎，QM=‎ ‎5‎ ‎2‎ ‎-2=‎ ‎1‎ ‎2‎ ‎， ∴∠3=90°-‎ ‎1‎ ‎2‎ ‎∠B， 而∠2+∠3=90°， ∴∠2=‎ ‎1‎ ‎2‎ ‎∠B， 又∵Rt△ABC≌Rt△DEF， ∴∠EDF=∠A=90°-∠B， 而∠1+∠EDF+∠2=90°， ∴∠1=‎ ‎1‎ ‎2‎ ‎∠B，即∠1=∠2， ∴△DQM∽△DPN， ∴PN：QM=DN：DM，即PN：‎ ‎1‎ ‎2‎ ‎=2：‎ ‎3‎ ‎2‎ ‎， ∴PN=‎ ‎2‎ ‎3‎ ‎， ∴AP=‎ ‎3‎ ‎2‎ ‎+‎ ‎2‎ ‎3‎ ‎=‎ ‎13‎ ‎6‎ ‎； （2）当DB=DQ，则Q点在C点，如图， DA=DC=‎ ‎5‎ ‎2‎ ‎， 而Rt△ABC≌Rt△DEF， ∴∠EDF=∠A， ∴△CPD∽△CDA， ∴CP：CD=CD：CA，即CP：‎ ‎5‎ ‎2‎ ‎=‎ ‎5‎ ‎2‎ ‎：3， ∴CP=‎ ‎25‎ ‎12‎ ‎， ∴AP=3-‎ ‎25‎ ‎12‎ ‎=‎ ‎11‎ ‎12‎ ‎； （3）当QB=QD，则∠B=∠BDQ， 而∠EDF=∠A， ∴∠EDF+∠BDQ=90°，即ED⊥AB，如图， ∴Rt△APD∽Rt△ABC， ∴AP：AB=AD：AC，即AP：5=‎ ‎5‎ ‎2‎ ‎：3， ∴AP=‎ ‎25‎ ‎6‎ ‎． 故答案为 ‎13‎ ‎6‎ 或 ‎11‎ ‎12‎ 或 ‎25‎ ‎6‎ ‎． 分类讨论：当BD=BQ，由AC=DF=3，BC=EF=4，则AB=5，过D作DM⊥BC与M，DN⊥AC于N，利用三角形的中位线的性质得到DM=AN=‎ ‎1‎ ‎2‎ AC=‎ ‎3‎ ‎2‎ ‎，BD=‎ ‎1‎ ‎2‎ AB=‎ ‎5‎ ‎2‎ ‎，DN=BM=‎ ‎1‎ ‎2‎ AC=2，可得到BQ与QM的长，然后利用等腰三角形的性质得到∠3=90°-‎ ‎1‎ ‎2‎ ‎∠B，易得∠2=‎ ‎1‎ ‎2‎ ‎∠B，又Rt△ABC≌Rt△DEF，利用三角形全等的性质得到∠EDF=∠A=90°-∠B，则∠1=‎ ‎1‎ ‎2‎ ‎∠B，即∠1=∠2，则△CPD∽△CDA，然后根据三角形相似的性质得到PN：QM=DN：DM，代值计算可得CP，从而求得AP； 当DB=DQ，则Q点在C点，易证△CPD∽△CDA，然后根据三角形相似的相似比即可得到CP，从而求得AP； 当QB=QD，则∠B=∠BDQ，而∠EDF=∠A，得到∠EDF+∠BDQ=90°，即ED⊥AB，易证Rt△APD∽Rt△ABC，然后根据三角形相似的相似比即可求得AP．‎ ‎013年门头沟区初三年级第二次统一练习 数学试卷评分参考 ‎ ‎ 一、选择题（本题共32分，每小题4分）‎ 题号 ‎1‎ ‎2‎ ‎3[来源:学科网ZXXK]‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 答案 D C B A C A B D,‎ 二、填空题（本题共16分，每小题4分）‎ 题号 ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 说明：12题第一、二空各1分，第三空2分 三、解答题（本题共30分，每小题5分）‎ ‎13．计算：．‎ 解： ‎ ‎= …………………………………………………4分 ‎= ． ……………………………………………………5分 ‎14．解：由题意可知D=0，即(-6)2-4(m-3)=0. ………………………………………………2分 解得m=12. …………………………………………………3分 当m=12时，原方程化为x2-6x+9=0. ……………………………………4分 解得x1=x2=3. ………………………………………………………5分 所以原方程的根为x1=x2=3.‎ ‎15．解：‎ ‎= ························································ 2分 ‎= ‎ ‎= ． ·················································································· 3分 当时，.··········································································· 4分 ‎∴原式==. ········································································ 5分 ‎16．证明：∵，，‎ ‎∴． ………………………………………………………1分 ‎∴．‎ 又∵，‎ ‎∴．‎ ‎∴．………………………2分 在和中，‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎∴．……………………4分 ‎∴．………………………………5分 ‎17．解：（1）∵ 点A（1, m）在一次函数y=3x的图象上，‎ ‎∴m=3． ……………………………1分 ‎∴ 点A的坐标为（1, 3）.‎ ‎∵ 点A（1, 3）在反比例函数的图象上，‎ ‎∴ . ………………………………2分 ‎ ∴反比例函数的解析式为. …………………………3分 ‎（2）点P的坐标为P (3, 9) 或P (-1, -3) . ……………………5分 ‎ 未完，更多内容请看下页 ‎ ‎18．解：设该校第二次有x人捐款，则第一次有（x–50）人捐款. ……………1分 根据题意，得. ………………………………………3分 解这个方程，得x=200. …………………………………4分 经检验，x=200是所列方程的解，并且符合实际问题的意义.‎ 答：该校第二次有200人捐款. ………………………………5分 ‎ ‎ 四、解答题（本题共20分，每小题5分）‎ ‎19．解：如图，过点D作DF⊥AC于F．‎ ‎∵∠DAB=60º，AC平分∠DAB，‎ ‎∴∠DAC=∠BAC=30°．‎ ‎∵，‎ ‎∴∠AFD=∠ACB=90°．‎ ‎∴，…………………………………………1分 BC= CE==4．………………………………………………2分 ‎∴．‎ ‎．……………………………3分 ‎∴．…………………………………………4分 ‎∴‎ ‎……………………………………………………………………5分 ‎ ‎ ‎20．（1）证明：连结OD．‎ ‎∵AB是⊙O的直径，‎ ‎∴∠ADB=90°． …………………………………1分 ‎∵∠A=30°，∴∠ABD=60°．‎ ‎∵∠ABD=2∠BDC，‎ ‎∴∠BDC =．‎ ‎∵OD=OB，∴△ODB是等边三角形．‎ ‎∴∠ODB=60°．‎ ‎∴∠ODC=∠ODB+∠BDC =90°．‎ ‎∴CD是⊙O的切线．……………………………………… 2分 ‎（2）解： ∵OF∥AD，∠ADB=90°，‎ ‎∴………3分 ‎∵BD=OB=2，‎ ‎∴．‎ ‎∴．……………………………… 4分 ‎∵OD=OB=2，∠DOC=60°，∠DOF=30°，‎ ‎∴，．‎ ‎∴． ……………………………………5分 ‎ ‎ ‎21．解：（1）这次共调查了学生50人，E组人数在这次调查中所占的百分比是％．……2分 ‎（2）表1中a的值是15，………………………………………………3分 补全图1．……………………………………………………………4分 ‎（3）54人．………………………………………………………………5分 ‎22．解：（1）利用正方形网格在图3上画出矩形ABCD的反射四边形EFGH．……………2分 ‎（2）图2、图3中矩形ABCD的反射四边形EFGH的周长是定值，定值是.…3分 ‎（3）图2、图3中矩形ABCD的反射四边形EFGH的面积不是定值，它们的面积分别是16、12………………………………………………………………5分 ‎ ‎ 五、解答题（本题共22分，第23、24题各7分，第25题8分）‎ ‎23．解：（1）∵拋物线经过原点，‎ ‎∴m2-6m+8=0．解得m1=2，m2=4．‎ 由题意知m¹4，‎ ‎∴m=2．……………………………………………………………1分 ‎∴拋物线的解析式为．…………………………………2分 ‎（2）∵点B(-2,n)在拋物线上，‎ ‎∴n=3．………………………………………………………………3分 ‎∴B点的坐标为(–2，3) ．‎ ‎∵直线l的解析式为，直线l经过B点，‎ ‎∴．‎ ‎∴．……………………………………………………………4分 ‎（3）∵拋物线的对称轴为直线x=2，直线l的解析式为y=-2x-1，‎ ‎∴拋物线的对称轴与x轴的交点C的坐标为(2,0)，‎ 直线l与y轴、直线x=2的交点坐标分别为 D(0,-1)、E(2,-5).‎ 过点B作BG⊥直线x=2于G，与y轴交于F.‎ ‎ 则BG=4.‎ 在Rt△BGC中，.‎ ‎∵CE=5，∴ CB=CE.‎ 过点E作EH⊥y轴于H.‎ 则点H的坐标为 (0,-5).‎ ‎∵点F、D的坐标为F(0,3)、D(0,-1)，‎ ‎∴FD=DH=4，BF=EH=2，∠BFD=∠EHD=90°.‎ ‎∴△DFB≌△DHE .‎ ‎∴DB=DE.‎ ‎∵PB=PE，‎ ‎∴点P在直线CD上.‎ ‎∴符合条件的点P是直线CD与该抛物线的交点.‎ 设直线CD的解析式为y=kx+a.‎ 将D(0,-1)、C(2,0)代入，得 解得 ‎ ‎∴ 直线CD的解析式为. ………………………………5分 设点P的坐标为(x，)，‎ ‎∴=.‎ 解得 ，.‎ ‎∴，.‎ ‎∴点P的坐标为(，)或(，).…………7分 未完，更多内容请看下页 ‎ ‎24．解：（1）线段AD与OM之间的数量关系是AD =2OM，位置关系是.………2分 ‎（2）（1）的两个结论仍然成立.‎ 证明：如图2，延长BO到F，使FO=BO，连结CF.‎ ‎∵M为BC中点，O为BF中点，∴MO为的中位线.‎ ‎∴FC =2OM. ………………………………3分 ‎∵∠AOB =∠AOF=∠COD=90°，‎ ‎ ‎ ‎ ‎ ‎∴∠AOD =∠FOC .‎ ‎ ‎ ‎∵AO =FO，CO=DO，‎ ‎∴△AOD≌△FOC.‎ ‎∴FC=AD.‎ ‎∴AD =2OM. ………………………………………4分 ‎∵MO为的中位线，∴MO∥CF .‎ ‎∴∠MOB =∠F.‎ 又∵≌，∴=.‎ ‎∵+=90°,‎ ‎∴+=90°.‎ 即. ……………………………………………………………………5分 ‎（3）（1）中线段AD与OM之间的数量关系没有发生变化.‎ 证明：如图3，延长DC交AB于E，连结ME，‎ 过点E作于N.‎ ‎∵OA＝OB，OC＝OD，，‎ ‎∴.‎ ‎∴AE＝DE，BE＝CE，∠AED=90°.‎ ‎∴DN=AN. ∴AD＝2NE.‎ ‎∵M为BC的中点，∴.‎ ‎∴四边形ONEM是矩形.‎ ‎∴NE＝OM.‎ ‎∴AD＝2OM. ………………………………………………………7分 ‎25. 解：（1）设直线AC的解析式为 ‎∵直线AC经过G(0，6)、C（3，0）两点，‎ ‎∴ 解这个方程组，得 ……………………1分 ‎∴直线AC的解析式为．……………………………2分 ‎（2）当x=1时，y=4. ∴A（1，4）.‎ ‎∵AP=CQ= t，‎ ‎∴点P（1，4-t）.……………………………………………3分 将y=4–t代入中，得点E的横坐标为x=.‎ ‎∴点E到CD的距离为.‎ ‎∴S△CQE=== ……………………………4分 ‎∴当t=2时，S△CQE最大，最大值为1.……………………………5分 ‎（3）过点E作FM∥DC，交AD于F，交BC于M．‎ 当点H在点E的下方时，连结CH.‎ ‎∵，∴.‎ ‎∵，∴.‎ ‎∵四边形CQEH为菱形，∴.‎ 在Rt△HMC中，由勾股定理得.‎ ‎∴.‎ 整理得 .‎ 解得 ，（舍）.‎ ‎∴当时，以C，Q，E，H为顶点的四边形是菱形. ……………7分 当点H在点E的上方时，同理可得当时. 以C，Q，E，H为顶点的四边形是菱形. …………………………………………8分 ‎∴的值是或 ‎ ‎