2009年山西省初中毕业学业考试数学试卷及答案 10页

‎2009年山西省初中毕业学业考试试卷 数 学 一、选择题（每小题2分，共20分）‎ ‎1．比较大小： （填“＞”、“=”或“＜“）．‎ A B C D ‎1‎ ‎（第5题）‎ ‎2．山西有着丰富的旅游资源，如五台山、平遥古城、乔家大院等著名景点，吸引了众多的海内外游客，2008年全省旅游总收入739.3亿元，这个数据用科学记数法可表示为 ．‎ ‎3．请你写出一个有一根为1的一元二次方程： ．‎ ‎4．计算：= ．‎ ‎5．如图所示，、、、是圆上的点，‎ 则 度．‎ ‎6．李师傅随机抽查了本单位今年四月份里6天的日用水量（单位：吨）结果如下：7，8，8，7，6，6，根据这些数据，估计四月份本单位用水总量为 吨． ‎ ‎7．如图，与是位似图形，且顶点都在格点上，则位似中心的坐标是 ．‎ x O A B C ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎（第7题）‎ A C D B E O ‎（第8题）‎ ‎8．如图，的对角线、相交于点，点是的中点，的周长为‎16cm，则的周长是 cm．‎ ‎9．若反比例函数的表达式为，则当时，的取值范围是 ．‎ ‎10．下列图案是晋商大院窗格的一部分，其中“○”代表窗纸上所贴的剪纸，则第个图中所贴剪纸“○”的个数为 ．‎ ‎（1）‎ ‎（2）‎ ‎（3）‎ ‎……‎ ‎……‎ ‎（第10题）‎ 二、选择题（在下列各小题中，均给出四个备选答案，‎ 其中只有一个正确答案，请将正确答案的字母号填入下表相应的空格内，每小题3分，共24分）‎ ‎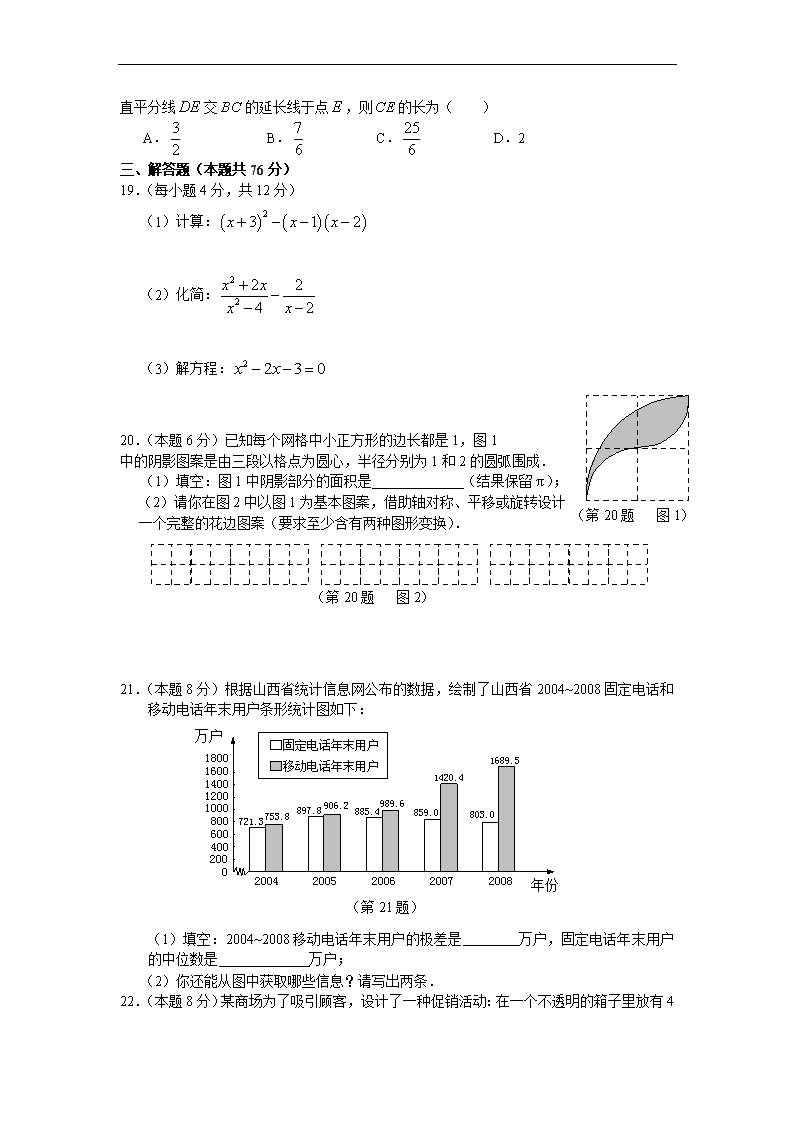11．下列计算正确的是（ ）‎ A． B．‎ C． D． ‎ ‎12．反比例函数的图象经过点，那么的值是（ ）‎ ‎ A． B． C． D．6 ‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎13．不等式组的解集在数轴上可表示为（ ）‎ ‎ A． B．‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎ ‎ C． D．‎ ‎14．解分式方程，可知方程（ ）‎ A．解为 B．解为 C．解为 D．无解 ‎ ‎15．如图是由几个相同的小正方体搭成的几何体的三视图，则搭成这个几何体的小正方体的个数是（ ）‎ 主视图 左视图 俯视图 俯视图 ‎（第15题）‎ ‎ A．5 B．‎6 C．7 D．8‎ ‎16．如图，是的直径，是的切线，点在上，，则的长为（ ）‎ A B C ‎（第16题）‎ m n n n ‎（2）‎ ‎（1）‎ ‎（第17题）‎ ‎ A． B． C． D．‎ ‎17．如图（1），把一个长为、宽为的长方形（）沿虚线剪开，拼接成图（2），成为在一角去掉一个小正方形后的一个大正方形，则去掉的小正方形的边长为（ ）‎ A． B． C． D．‎ A D B E C ‎（第18题）‎ ‎18．如图，在中，的垂 直平分线交的延长线于点，则的长为（ ）‎ A． B． C． D．2‎ 三、解答题（本题共76分）‎ ‎19．（每小题4分，共12分）‎ ‎（1）计算：‎ ‎（2）化简：‎ ‎（3）解方程：‎ ‎（第20题 图1）‎ ‎20．（本题6分）已知每个网格中小正方形的边长都是1，图1‎ 中的阴影图案是由三段以格点为圆心，半径分别为1和2的圆弧围成．‎ ‎（1）填空：图1中阴影部分的面积是 （结果保留）；‎ ‎（2）请你在图2中以图1为基本图案，借助轴对称、平移或旋转设计 一个完整的花边图案（要求至少含有两种图形变换）．‎ ‎（第20题 图2）‎ ‎21．（本题8分）根据山西省统计信息网公布的数据，绘制了山西省2004~2008固定电话和移动电话年末用户条形统计图如下：‎ ‎0‎ ‎200‎ ‎400‎ ‎600‎ ‎800‎ ‎1000‎ ‎1200‎ ‎1400‎ ‎1600‎ ‎1800‎ 年份 万户 固定电话年末用户 移动电话年末用户 ‎2004‎ ‎2005‎ ‎2006‎ ‎2007‎ ‎2008‎ ‎721.3‎ ‎753.8‎ ‎897.8‎ ‎906.2‎ ‎885.4‎ ‎989.6‎ ‎859.0‎ ‎1420.4‎ ‎1689.5‎ ‎803.0‎ ‎（第21题）‎ ‎（1）填空：2004~2008移动电话年末用户的极差是 万户，固定电话年末用户的中位数是 万户；‎ ‎（2）你还能从图中获取哪些信息？请写出两条．‎ ‎22．（本题8分）‎ 某商场为了吸引顾客，设计了一种促销活动：在一个不透明的箱子里放有4个相同的小球，球上分别标有“0元”、“10元”、“20元”和“30元”的字样．规定：顾客在本商场同一日内，每消费满200元，就可以在箱子里先后摸出两个球（第一次摸出后不放回）．商场根据两小球所标金额的和返还相应价格的购物券，可以重新在本商场消费．某顾客刚好消费200元．‎ ‎（1）该顾客至少可得到 元购物券，至多可得到 元购物券；‎ ‎（2）请你用画树状图或列表的方法，求出该顾客所获得购物券的金额不低于30元的概率．‎ ‎（第23题）‎ A B C D E F 水深 ‎23．（本题8分）有一水库大坝的横截面是梯形，为水库的水面，点在上，某课题小组在老师的带领下想测量水的深度，他们测得背水坡的长为‎12米，迎水坡上的长为‎2米，求水深．（精确到‎0.1米，）‎ ‎24．（本题8分）某批发市场批发甲、乙两种水果，根据以往经验和市场行情，预计夏季某一段时间内，甲种水果的销售利润（万元）与进货量（吨）近似满足函数关系；乙种水果的销售利润（万元）与进货量（吨）近似满足函数关系（其中为常数），且进货量为1吨时，销售利润为1.4万元；进货量为2吨时，销售利润为2.6万元．‎ ‎（1）求（万元）与（吨）之间的函数关系式．‎ ‎（2）如果市场准备进甲、乙两种水果共10吨，设乙种水果的进货量为吨，请你写出这两种水果所获得的销售利润之和（万元）与（吨）之间的函数关系式．并求出这两种水果各进多少吨时获得的销售利润之和最大，最大利润是多少？‎ ‎25．（本题12分）在中，将绕点 顺时针旋转角得交于点，分别交于两点．‎ A D B E C F A D B E C F ‎（第25题 图1）‎ ‎（第25题 图2）‎ ‎（1）如图1，观察并猜想，在旋转过程中，线段与有怎样的数量关系？并证明你的结论；‎ ‎（2）如图2，当时，试判断四边形的形状，并说明理由；‎ ‎（3）在（2）的情况下，求的长．‎ ‎26．（本题14分）如图，已知直线与直线相交于点分别交轴于两点．矩形的顶点分别在直线上，顶点都在轴上，且点与点重合．‎ ‎ （1）求的面积；‎ ‎（2）求矩形的边与的长；‎ A D B E O C F x y y ‎（G）‎ ‎（第26题）‎ ‎（3）若矩形从原点出发，沿轴的反方向以每秒1个单位长度的速度平移，设移动时间为秒，矩形与重叠部分的面积为，求关于的函数关系式，并写出相应的的取值范围．‎ ‎2009年山西省初中毕业学业考试试卷 数 学 一、选择题（每小题2分，共20分）‎ ‎1．＞ 2． 3．答案不唯一，如 4． 5．30‎ ‎6．210 7．（9，0） 8．8 9． 10．‎ 二、选择题（在下列各小题中，均给出四个备选答案，其中只有一个正确答案，请将正确答案的字母号填入下表相应的空格内，每小题3分，共24分）‎ 题 号 ‎11‎ ‎12‎ ‎13‎ ‎14‎ ‎15‎ ‎16‎ ‎17‎ ‎18‎ 答 案 D C D D B A A B 三、解答题（本题共76分）‎ ‎19．（1）解：原式= （2分）‎ ‎ = （3分）‎ ‎ =． （4分）‎ ‎（2）解：原式= （2分）‎ ‎ = （3分）‎ ‎ =1． （4分）‎ ‎（3）解：移项，得配方，得 （2分）‎ ‎ ∴∴ （4分）‎ ‎ （注：此题还可用公式法，分解因式法求解，请参照给分）‎ ‎20．解：（1）； （2分）‎ ‎（2）答案不唯一，以下提供三种图案．‎ ‎（第20题 图2） （6分）‎ ‎（注：如果花边图案中四个图案均与基本图案相同，则本小题只给2分；未画满四个“田”字格的，每缺1个扣1分．）‎ ‎21．（1）935.7，859.0； （4分）‎ ‎ （2）解：2004~2008移动电话年末用户逐年递增．‎ ‎ 2008年末固定电话用户达803.0万户． （8分）‎ ‎ （注：答案不唯一，只要符合数据特征即可得分）‎ ‎22．解：（1）10，50； （2分）‎ ‎ （2）解：解法一（树状图）：‎ ‎0‎ ‎10‎ ‎20‎ ‎30‎ ‎10‎ ‎20‎ ‎30‎ ‎10‎ ‎0‎ ‎20‎ ‎30‎ ‎10‎ ‎30‎ ‎40‎ ‎0‎ ‎10‎ ‎30‎ ‎20‎ ‎20‎ ‎30‎ ‎50‎ ‎20‎ ‎30‎ ‎0‎ ‎10‎ ‎50‎ ‎30‎ ‎40‎ 第一次 第二次 和 ‎ （6分）‎ 从上图可以看出，共有12种可能结果，其中大于或等于30元共有8种可能结果，因此（不低于30元）= （8分）‎ 解法二（列表法）：‎ 第一次 第二次 ‎0‎ ‎10‎ ‎20‎ ‎30‎ ‎0‎ ‎10‎ ‎20‎ ‎30‎ ‎10‎ ‎10‎ ‎30‎ ‎40‎ ‎20‎ ‎20‎ ‎30‎ ‎50‎ ‎30‎ ‎30‎ ‎40‎ ‎50‎ ‎ （6分）‎ ‎（以下过程同“解法一”） （8分）‎ ‎（第23题）‎ A B C D E F M G H 水深 ‎23．解：分别过作于于过作于则四边形为矩形．‎ ‎∴‎ 在中，‎ ‎∴ （3分）‎ 在中， （6分）‎ ‎∴ （7分）‎ 答：水深约为‎6.7米． （8分）‎ ‎（其它解法可参照给分）‎ ‎24．解：（1）由题意，得：解得 （2分）‎ ‎ ∴ （3分）‎ ‎（2）‎ ‎ ∴ （5分）‎ ‎ ∴时，有最大值为6.6. （7分）‎ ‎∴（吨）.‎ 答：甲、乙两种水果的进货量分别为4吨和6吨时，获得的销售利润之和最大，最大利润是6.6万元. （8分）‎ ‎25．解：（1） （1分）‎ 证明：（证法一）‎ 由旋转可知，‎ ‎∴ （3分）‎ ‎∴又 ‎∴即 （4分）‎ ‎（证法二）‎ 由旋转可知，而 ‎∴ （3分）‎ ‎∴∴‎ 即 （4分）‎ ‎ （2）四边形是菱形. （5分）‎ 证明：同理 ‎∴四边形是平行四边形. （7分）‎ A D B E C F G 又∴四边形是菱形. （8分）‎ ‎ （3）（解法一）过点作于点，则 在中，‎ ‎……（10分）‎ 由（2）知四边形是菱形，‎ ‎∴‎ ‎∴ （12分）‎ ‎（解法二）∴‎ 在中，‎ ‎ （10分）‎ ‎∴ （12分）‎ ‎（其它解法可参照给分）‎ ‎26．（1）解：由得点坐标为 由得点坐标为 ‎∴ （2分）‎ 由解得∴点的坐标为 （3分）‎ ‎∴ （4分）‎ ‎ （2）解：∵点在上且 ‎ ∴点坐标为 （5分）‎ 又∵点在上且 ‎∴点坐标为 （6分）‎ ‎∴ （7分）‎ ‎ （3）解法一：当时，如图1，矩形与重叠部分为五边形（时，为四边形）．过作于，则 A D B E O R F x y y M ‎（图3）‎ G C A D B E O C F x y y G ‎（图1）‎ R M A D B E O C F x y y G ‎（图2）‎ R M ‎∴即∴‎ ‎∴‎ 即 （10分）‎