2011宜昌试题中考数学试题 10页

湖北宜昌2011年初中毕业学业考试数学试题 本试卷共24小题，满分120分，考试时间120分钟．‎ 注意事项：‎ 本试卷分试题卷和答题卡两部分，请将答案答在答题卡上每题对应的答题区域内，答在试题卷上无效。‎ 考试结束，请将本试题卷和答题卡一并上交。‎ 以下数据、公式供参考： ≈1.7；l弧长=πR(R为半径，l为弧长)；二次函数y＝ax2＋bx＋c图象的顶点坐标是（）。‎ ‎ ‎ 一、选择题 (在各小题给出的四个选项中，只有一项是符合题目要求的，请在答题卡上指定的位置填涂符合要求的选项前面的字母代号.本大题共15小题，每小题3分，计45分)‎ ‎1．如图，用数学的眼光欣赏这个蝴蝶图案，它的一种数学美体现在蝴蝶图案的（■）.‎ ‎(A)轴对称性 (B)用字母表示数 (C)随机性 (D)数形结合 ‎2．如果用＋0.02克表示一只乒乓球质量超出标准质量0.02克，那么一只乒乓球质量低于标准质量0.02克记作（■）.‎ ‎(A)＋0.02克  (B)－0.02克 (C) 0克  (D)＋0.04克 ‎3．要调查城区九年级8000名学生了解禁毒知识的情况，下列调查方式最合适的是（■）.‎ ‎(A)在某校九年级选取50名女生 (B)在某校九年级选取50名男生 ‎(C)在某校九年级选取50名学生 (D)在城区8000名九年级学生中随机选取50名学生 ‎4．我市大约有34万中小学生参加了“廉政文化进校园”教育活动，将数据34万用科学记数法表示，正确的是（■ ）.‎ ‎(A)0.34×105  (B)3.4×105 (C)34×105  (D)340×105‎ ‎5．如图，数轴上A，B两点分别对应实数a，b，则下列结论正确的是（ ■）.‎ ‎(A)a＜b (B)a＝b (C)a＞b (D)ab＞0‎ ‎6．如图，在一间黑屋子里用一盏白炽灯照一个球，球在地面上的阴影的形状是一个圆，当把白炽灯向远移时，圆形阴影的大小的变化情况是（■）.‎ ‎(A)越来越小 (B)越来越大 (C)大小不变 (D)不能确定 ‎7．下列计算正确的是（■）.‎ ‎(A)3a－a＝3  (B)2a·a3＝a6 （C)(3a3)2＝2a6  (D)2a÷a＝2‎ ‎8．一个圆锥体按如图所示摆放，它的主视图是（■）.‎ ‎9．按图1的方法把圆锥的侧面展开，得到图2，其半径OA＝3，圆心角∠AOB＝120°，则AB的长为（■）.‎ ‎(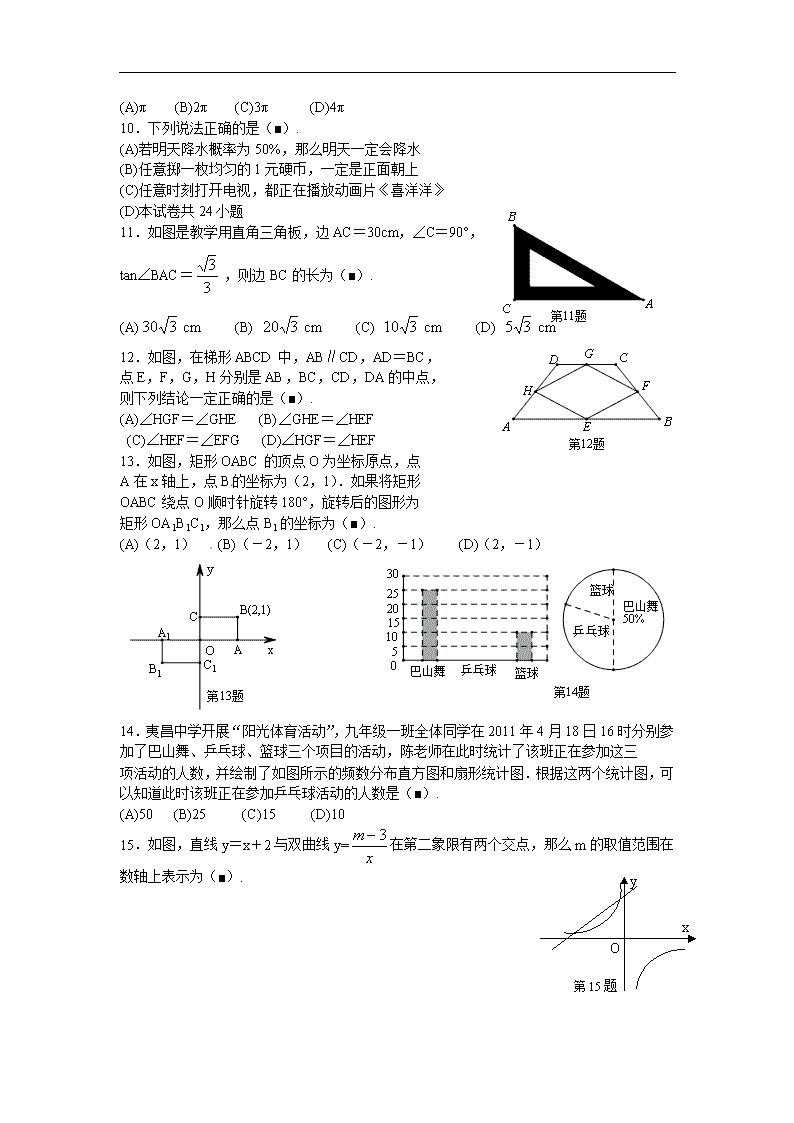A)π (B)2π (C)3π (D)4π ‎10．下列说法正确的是（■）.‎ ‎(A)若明天降水概率为50%，那么明天一定会降水 ‎(B)任意掷一枚均匀的1元硬币，一定是正面朝上 ‎(C)任意时刻打开电视，都正在播放动画片《喜洋洋》‎ ‎(D)本试卷共24小题[来源:学科网ZXXK]‎ ‎11．如图是教学用直角三角板，边AC＝30cm，∠C＝90°，‎ tan∠BAC＝ ，则边BC的长为（■）.‎ ‎(A) cm (B)  cm (C)  cm (D)  cm ‎12．如图，在梯形ABCD中，AB∥CD，AD＝BC，‎ 点E，F，G，H分别是AB，BC，CD，DA的中点，‎ 则下列结论一定正确的是（■）.‎ ‎(A)∠HGF＝∠GHE (B)∠GHE＝∠HEF ‎ ‎ (C)∠HEF＝∠EFG (D)∠HGF＝∠HEF ‎13．如图，矩形OABC的顶点O为坐标原点，点 A在x轴上，点B的坐标为（2，1）．如果将矩形 OABC绕点O顺时针旋转180°，旋转后的图形为 矩形OA1B1C1，那么点B1的坐标为（■）.‎ ‎(A)（2，1） (B)（－2，1） (C)（－2，－1） (D)（2，－1）‎ ‎14．夷昌中学开展“阳光体育活动”，九年级一班全体同学在‎2011年4月18日16时分别参加了巴山舞、乒乓球、篮球三个项目的活动，陈老师在此时统计了该班正在参加这三 项活动的人数，并绘制了如图所示的频数分布直方图和扇形统计图．根据这两个统计图，可以知道此时该班正在参加乒乓球活动的人数是（■）. ‎ ‎(A)50 (B)25 (C)15 (D)10‎ x O 第15题 y ‎15．如图，直线y＝x＋2与双曲线y=在第二象限有两个交点，那么m的取值范围在数轴上表示为（■）.‎ ‎[来源:学科网ZXXK]‎ 二、解答题  (请将解答结果书写在答题卡上指定的位置．本大题共9小题，16～19每小题7分，20～21每小题8分，22～23每小题10分，24题11分，合计75分)‎ ‎16．先将代数式化简，再从－1，1两数中选取一个适当的数作为x的值代入求值．‎ ‎17．解方程组.‎ ‎18．如图，在平行四边形ABCD中，E为BC中点，AE的延长线与DC的延长线相交于点F.‎ ‎（1）证明：∠DFA＝∠FAB；‎ ‎（2）证明：△ABE≌△FCE．‎ ‎19．某市实施“限塑令”后，2008年大约减少塑料消耗约4万吨．调查结果分析显示，从2008年开始，五年内该市因实施“限塑令”而减少的塑料消耗量y(万吨)随着时间x(年)逐年成直线上升，y与x之间的关系如图所示.[来源:学_科_网Z_X_X_K]‎ ‎（1）求y与x之间的关系式；‎ ‎（2）请你估计，该市2011年因实施“限塑令”而减少的塑料消耗量为多少？‎ ‎20．如图，某商标是由边长均为2的正三角形、正方形、正六边形的金属薄片镶嵌而成的镶嵌图案.‎ ‎（1）求这个镶嵌图案中一个正三角形的面积；‎ ‎（2）如果在这个镶嵌图案中随机确定一个点O，那么点O落在镶嵌图案中的正方形区域的概率为多少？(结果保留二位小数）‎ ‎21．如图，D是△ABC的边BC的中点,过AD延长线上的点E作AD的垂线EF，E为垂足，EF与AB的延长线相交于点F，点O在AD上，AO＝CO，BC∥EF．‎ ‎(1)证明：AB＝AC；‎ ‎(2)证明：点O是△ABC的外接圆的圆心；‎ ‎(3)当AB＝5，BC＝6时，连接BE，若∠ABE＝90°，求AE的长．‎ ‎22．随着经济的发展，尹进所在的公司每年都在元月一次性的提高员工当年的月工资。尹进2008年的月工资为2000元，在2010年时他的月工资增加到2420元，他2011年的月工资按2008到2010年的月工资的平均增长率继续增长．‎ ‎（1）尹进2011年的月工资为多少?‎ ‎（2）尹进看了甲、乙两种工具书的单价，认为用自己2011年6月份的月工资刚好购买若干本甲种工具书和一些乙种工具书，当他拿着选定的这些工具书去付书款时，发现自己计算书款时把这两种工具书的单价弄对换了，故实际付款比2011年6月份的月工资少了242元，于是他用这242元又购买了甲、乙两种工具书各一本，并把购买的这两种工具书全部捐献给西部山区的学校．请问，尹进总共捐献了多少本工具书？‎ ‎[来源:学科网ZXXK]‎ ‎23．如图1，Rt△ABC两直角边的边长为AC＝1，BC＝2．‎ ‎（1）如图2，⊙O与Rt△ABC的边AB相切于点X，与边CB相切于点Y．请你在图2中作出并标明⊙O的圆心O；（用尺规作图，保留作图痕迹，不写作法和证明）‎ ‎（2）P是这个Rt△ABC上和其内部的动点,以P为圆心的⊙P与Rt△ABC的两条边相切．设⊙P的面积为s，你认为能否确定s的最大值？若能，请你求出s的最大值;若不能,请你说明不能确定s的最大值的理由．‎ ‎24．已知抛物线y＝ax2＋bx＋c与直线y＝mx＋n相交于两点，这两点的坐标分别是（0,）和（m－b，m2－mb＋n），其中a，b，c，m，n为实数,且a，m不为0．‎ ‎（1）求c的值；‎ ‎（2）设抛物线y＝ax2＋bx＋c与x轴的两个交点是（x1，0）和（x2，0），求x1x2的值；‎ ‎（3）当－1≤x≤1时，设抛物线y＝ax2＋bx＋c上与x轴距离最大的点为P（xo，yo ），求这时｜yo｜的最小值．‎ ‎[来源:学科网]‎ 参考答案与评分说明 ‎（一）阅卷评分说明 1．正式阅卷前先进行试评，在试评中认真阅读参考答案，明确评分标准，不得随意拔高或降低评分标准．试评的试卷必须在阅卷后期全部予以复查，防止阅卷前后期评分标准宽严不一致．‎ ‎2.评分方式为分小题分步累计评分，解答过程的某一步骤发生笔误，只要不降低后继部分的难度，而后继部分再无新的错误，后继部分可评应得分数的50%；若是几个相对独立的得分点，其中一处错误不影响其它得分点的评分．‎ ‎3.最小记分单位为1分，不得将评分标准细化至1分以下(即不得记小数分)．因实行网上双人阅卷得到的最后总分按四舍五入取整.‎ ‎4.发现解题中的错误后仍应继续评分，直至将解题过程评阅完毕，确定最后得分点后，再评出该题实际得分．‎ ‎5.本参考答案只给出一种或几种解法，凡有其它正确解法都应参照本评分说明分步确定得分点，并同样实行分小题分步累计评分．‎ ‎6.合理精简解题步骤者，其简化的解题过程不影响评分．‎ ‎（二）参考答案及评分标准     一、选择题（每小题3分，计45分）‎ 题号 ‎1[来源:学科网ZXXK]‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ ‎13‎ ‎14‎ ‎15‎ 答案 A B D B C A D A B D C D C C B 二、解答题（本大题有9小题，计75分）‎ ‎16．解：原式＝ （3分,省略不扣分）   ＝x （6分）‎ ‎ 当x＝1时，原式＝1．（7分）（直接代入求值得到1，评4分）‎ ‎17．解：由①，得x＝y＋1，（2分），代入②，得2(y＋1)+y＝2． （3分）‎ 解得y＝0． （4分）， 将y＝0代入①，得x＝1． （6分）‎ ‎[或者：①+②，得3x＝3，（2分）∴x＝1． （3分）‎ 将x＝1代入①，得1－y＝1， （4分）  ∴y＝0．（6分）]‎ ‎∴原方程组的解是. （7分）‎ ‎18.证明：‎ ‎（1）∵AB与CD是平行四边形ABCD的对边，∴AB∥CD，（1分）∴∠F=∠FAB．（3分）（2）在△ABE和△FCE中，‎ ‎   ∵   ∠FAB=∠F （4分） ∠AEB=∠FEC  （5分） BE=CE （6分）‎ ‎   ∴ △ABE≌△FCE． （7分）‎ ‎19．解：（1）设y=kx+b.  (1分)‎ 由题意，得(3分）.解得 （5分）‎ ‎∴y＝x－2004．‎ ‎（2）当x＝2011时，y＝2011－2004 (6分) ‎ ‎＝7. (7分)‎ ‎∴该市2011年因“限塑令”而减少的塑料消耗量约为7万吨.‎ ‎20.解:‎ ‎（1）∵图案中正三角形的边长为2，∴高为 .(1分)‎ ‎∴正三角形的面积为×2×  ＝  . (2分)‎ ‎（2）∵图中共有11个正方形， ∴图中正方形的面积和为11×(2×2)＝44.  (3分)‎ ‎∵图中共有2个正六边形，∴图中正六边形的面积和为2×(6××2×  )＝12 .(4分)∵图中共有10个正三角形，∴图中正三角形的面积和为10  .‎ ‎∵镶嵌图形的总面积为44＋10  ＋12 ＝44+22  (5分)≈81.4，‎ ‎∴点O落在镶嵌图案中正方形区域的概率为 (7分)≈0.54．(8分)‎ 答:点O落在镶嵌图案中正方形区域的概率为0.54.(“≈”写为“＝”不扣分)‎ ‎21．解:‎ ‎(1)∵AE⊥EF， EF∥BC，∴AD⊥BC． (1分)‎ 在△ABD和△ACD中，∵BD＝CD，∠ADB＝∠ADC，AD＝AD，‎ ‎∴△ABD≌△ACD． (或者：又∵BD＝CD，∴AE是BC的中垂线．)  (2分)‎ ‎∴AB＝AC．  (3分)‎ ‎(2)连BO，∵AD是BC的中垂线，∴BO＝CO． (或者：证全等也可得到BO＝CO．)‎ 又AO＝CO，∴AO＝BO＝CO． (4分)‎ ‎∴点O是△ABC外接圆的圆心．  (5分)‎ ‎（3）解法1：‎ ‎∵∠ABE＝∠ADB=90°，∴∠ABD+∠BAD=∠AEB+∠BAE=90°，‎ ‎∴∠ABD=∠AEB．  又∵∠BAD=∠EAB， ∴△ABD∽△AEB．‎ ‎∴ (或者：由三角函数得到)  （6分）‎ 在Rt△ABD中，∵AB=5，BD=BC=3， ∴AD=4． （7分）‎ ‎∴AE=． (8分)‎ 解法2：‎ ‎∵AO＝BO， ∴∠ABO＝∠BAO．‎ ‎∵∠ABE＝90°，∴∠ABO＋∠OBE＝∠BAO＋∠AEB＝90°．‎ ‎∴∠OBE＝∠OEB， ∴OB＝OE． (6分)‎ 在 Rt△ABD中，∵AB=5，BD=BC=3，∴AD=4．‎ ‎ 设 OB＝x， 则 OD＝4－x，由32+（4-x)2=x2,解得x=． (7分)‎ ‎∴AE＝2OB＝．(8分)‎ 解法3：‎ 设AO的延长线与⊙O交于点E1，则AE1是⊙O的直径， ∴∠ABE1=90°．‎ 在Rt△ABE和Rt△ABE1中，∵∠BAE＝∠BAE1，∠ABE＝∠ABE1＝90°，AB＝AB,‎ ‎∴△ABE≌△ABE1，∴AE=AE1．  (6分) (同方法2) ∵BO=． （7分）‎ ‎∴AE=2OB=． (8分)‎ ‎22.解:‎ ‎（1）设尹进2008到2010年的月工资的平均增长率为x,则,2000（1＋x）2＝2420． (1分)解 得 ，x1＝－2.1 ,  x2＝0.1,  (2分 ) x1＝－2.1与题意不合，舍去.‎ ‎∴尹进2011年的月工资为2420×(1＋0.1)=2662元.  (3分)‎ ‎（2）设甲工具书单价为m元，第一次选购y本.设乙工具书单价为n元，第一次选购z本.则由题意， 可列方程:m＋n＝242，  ①  (4分)‎ ny＋mz＝2662， ②  (6分)‎ my＋nz＝2662－242． ③ (7分)‎ ‎(②,③任意列对一个给2分;②,③全对也只给3分)‎ 由②＋③，整理得，（m＋n）（y＋z）＝2×2662－242，  (8分)‎ 由①,∴242（y＋z）＝2×2662－242，∴ y＋z＝22－1＝21． (9分)‎ 答：尹进捐出的这两种工具书总共有23本. (10分)  (只要得出23本，即评1分)‎ ‎23.解：‎ ‎(1)共2分.（标出了圆心，没有作图痕迹的评1分）看见垂足为Y（X）的一 条 垂 线 (或 者∠ABC的平分线)即评1分，‎ ‎(2)①当⊙P与Rt△ABC的边 AB和BC相切时，由角平分线的性质，动点P是∠ABC的平分线BM上的点.‎ 如图1，在∠ABC的平分线BM上任意确定点P1  (不为∠ABC的顶点)，‎ ‎∵ OX ＝BOsin∠ABM, P1Z＝BP1sin∠ABM．‎ 当 BP1＞BO 时 ，P1Z＞OX,即P与B的距离越大，⊙P的面积越大．‎ 这时，BM与AC的交点P是符合题意的、BP长度最大的点. ‎ ‎（3分.此处没有证明和结论不影响后续评分）‎ 如图2，∵∠BPA＞90°，过点P作PE⊥AB，垂足为E，则E在边AB上.‎ ‎∴以P为圆心、PC为半径作圆，则⊙P与边CB相切于C，与边AB相切于E，‎ 即这时的⊙P是符合题意的圆.（4分.此处没有证明和结论不影响后续评分）‎ 这时⊙P的面积就是S的最大值.‎ ‎∵∠A＝∠A，∠BCA＝∠AEP＝90°,∴ Rt△ABC∽Rt△APE， （5分）‎ ‎∴.‎ ‎∵AC＝1，BC＝2，∴AB＝.‎ 设PC＝x，则PA＝AC－PC＝1－x, PC＝PE，‎ ‎∴， ∴x＝ ． （6分）‎ ‎②如图3，同理可得：当⊙P与Rt△ABC的边AB和AC相切时，设PC＝y，则 ，‎ ‎∴y= . （7分）[来源:学科网ZXXK]‎ ‎③如图4，同理可得：当⊙P与Rt△ABC的边BC和AC相切时，‎ 设PF＝z，则， ∴z=. （8分）‎ 由①，②，③可知：∵  ＞2，∴ ＋2＞＋1＞3，‎ ‎∵当分子、分母都为正数时，若分子相同，则分母越小，这个分数越大，‎ ‎(或者:∵x= =2-4, y= = 5, ‎ ‎∴y-x=>0, ∴y>x. ∵z-y=>0)‎ ‎∴2， （9分，没有过程直接得出酌情扣1分）‎ ‎∴ z＞y＞x. ∴⊙P的面积S的最大值为. （10分）‎ ‎24．解:‎ ‎(1)∵（0，）在y＝ax2＋bx＋c上，∴ ＝a×02＋b×0＋c， ∴ c＝.(1分)‎ ‎(2)又可得 n＝.‎ ‎∵ 点（m－b，m2－mb＋n）在y＝ax2＋bx＋c上，‎ ‎∴ m2－mb＝a（m－b）2＋b（m－b），‎ ‎∴（a－1）（m－b）2＝0， （2分）‎ 若（m－b）＝0，则（m－b， m2－mb＋n）与（0，）重合，与题意不合．‎ ‎∴ a＝1．（3分，只要求出a＝1，即评3分）‎ ‎∴抛物线y＝ax2＋bx＋c，就是y＝x2＋bx．‎ ‎△＝b2－4ac＝b2－4×（）＞0，（没写出不扣分）‎ ‎∴抛物线y＝ax2＋bx＋c与x轴的两个交点的横坐标就是关于x的二次方程0＝ax2＋bx＋c的两个实数根，∴由根与系数的关系，得x1x2＝． （4分）‎ ‎(3)抛物线y＝x2＋bx的对称轴为x＝，最小值为． （没写出不扣分）‎ 设抛物线y＝x2＋bx在x轴上方与x轴距离最大的点的纵坐标为H，在x轴下方与x轴距离最大的点的纵坐标为h．‎ ‎①当<－1，即b＞2时，在x轴上方与x轴距离最大的点是（1，yo），‎ ‎∴｜H｜＝yo＝＋b＞，  (5分)‎ 在x轴下方与x轴距离最大的点是（－1，yo），‎ ‎∴｜h｜＝｜yo｜＝｜－b｜＝b－＞， (6分) ‎ ‎ ∴｜H｜＞｜h｜．∴这时｜yo｜的最小值大于. (7分)‎ ‎② 当－1≤≤0，即0≤b≤2时，‎ 在x轴上方与x轴距离最大的点是（1，yo），‎ ‎∴｜H｜＝yo＝＋b≥，当b＝0时等号成立.‎ 在x轴下方与x轴距离最大点的是 （，），‎ ‎∴｜h｜＝｜｜＝≥，当b＝0时等号成立.‎ ‎∴这时｜yo｜的最小值等于. (8分)‎ ‎③ 当0＜≤1，即－2≤b＜0时,‎ 在x轴上方与x轴距离最大的点是（－1，yo），‎ ‎∴｜H｜＝yo＝｜1＋（－1）b｜＝｜－b｜＝－b＞‎ 在x轴下方与x轴距离最大的点是 （，），‎ ‎∴｜h｜＝｜yo｜＝｜｜＝＞.‎ ‎∴ 这 时 ｜yo｜的 最 小 值 大 于 . (9分)‎ ‎④ 当1＜，即b＜－2时，‎ 在x轴上方与x轴距离最大的点是（－1，yo），∴｜H｜＝－b＞,‎ 在x轴下方与x轴距离最大的点是(1，yo)，∴｜h｜＝｜＋b｜＝－（b＋）＞，‎ ‎∴｜H｜＞｜h｜,∴这时｜yo｜的最小值大于.  (10分)‎ 综上所述，当b＝0，x0＝0时，这时｜yo｜取最小值，为｜yo｜＝.  (11分)‎