中考压轴题分类专题二线段和差的最值问题 8页

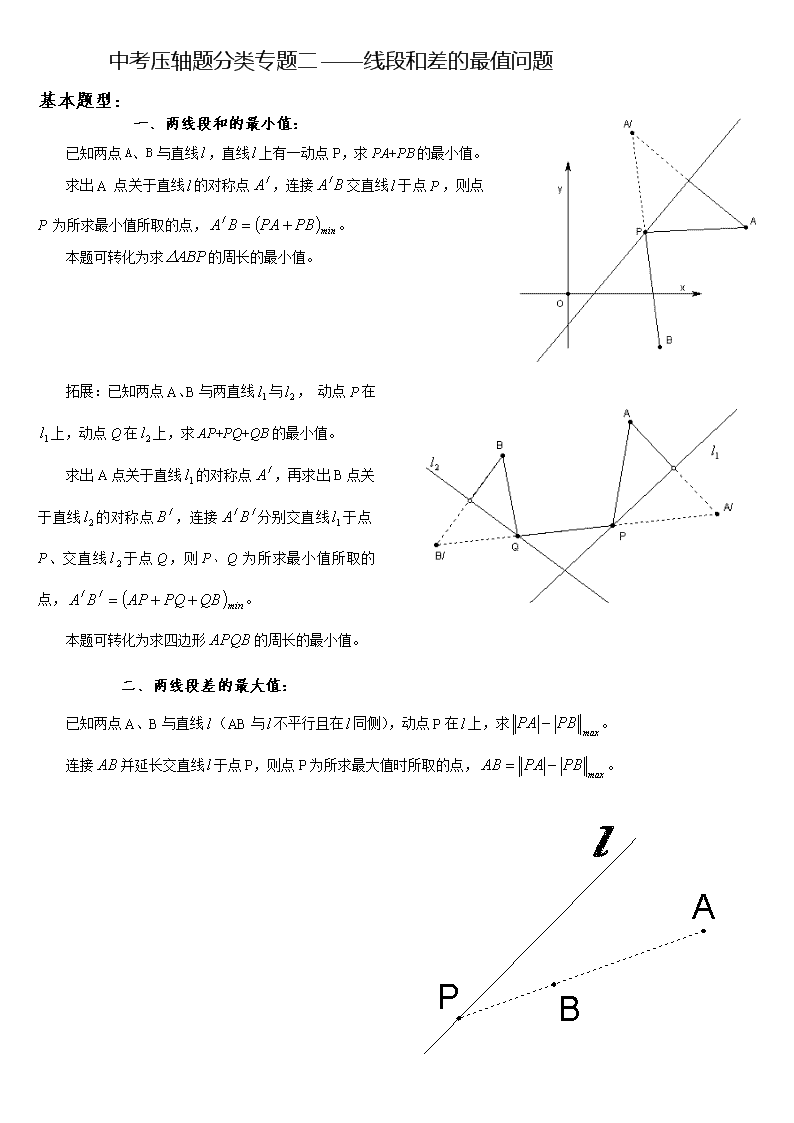
中考压轴题分类专题二——线段和差的最值问题 基本题型：一、两线段和的最小值：‎ 已知两点A、B与直线，直线上有一动点P，求PA+PB的最小值。‎ 求出A点关于直线的对称点，连接交直线于点P，则点P为所求最小值所取的点，。‎ 本题可转化为求的周长的最小值。‎ 拓展：已知两点A、B与两直线与， 动点P在上，动点Q在上，求AP+PQ+QB的最小值。‎ 求出A点关于直线的对称点，再求出B点关于直线的对称点，连接分别交直线于点P、交直线于点Q，则P、Q为所求最小值所取的点，。‎ 本题可转化为求四边形的周长的最小值。‎ 二、两线段差的最大值：‎ 已知两点A、B与直线（AB与不平行且在同侧），动点P在上，求。‎ 连接并延长交直线于点P，则点P为所求最大值时所取的点，。‎ 所需知识点：‎ 一、 中点公式：‎ 已知两点，则线段PQ的中点M为。‎ 拓展：三角形的重心（三中线交点）公式：‎ 已知的顶点分别为，则的重心G为。‎ 二、 直线的斜率：‎ ‎ 直线的斜率是指直线与轴正方向所成角的正切值。时，；时，。已知两点，则直线PQ的斜率： 。‎ 三、 平面内两直线之间的位置关系：‎ 两直线分别为：，。‎ ‎（一）∥。（二）与相交。特别是。‎ 四、 求已知点关于已知直线的对称点：‎ 已知点与直线，求点关于直线的对称点。‎ 过点作直线的垂线。则，又因为过点，将代入，既可求出。将与联立得，既可求出垂足点的坐标。因为为线段的中点，所以利用中点公式可求得为。‎ 典型例题课后练习：‎ 例一（09深中四月月考）：已知：抛物线与轴交于A（1，0），B（5，0）两点，与轴交于点M，抛物线的顶点为P，且。‎ ‎（1）求P点的坐标及抛物线的解析式； （5）‎ ‎（2）求的面积（O为坐标原点）； （2）‎ ‎（3）在抛物线的对称轴上是否存在一点Q，‎ 使的周长最短？若存在，请求出Q 点的坐标；若不存在，请说明理由。 （2）‎ 例二（05深圳中考题）已知△ABC是边长为4的等边三角形，BC在x轴上，点D为BC的中点，点A在第一象限内，AB与y轴的正半轴相交于点E，点B（-1，0），P是AC上的一个动点（P与点A、C不重合）‎ ‎ （1）（2分）求点A、E的坐标；‎ ‎ （2）（2分）若y=过点A、E，求抛物线的解析式。‎ ‎ （3）（5分）连结PB、PD，设L为△PBD的周长，当L取最小值时，求点P的坐标及L的最小值，并判断此时点P是否在（2）中所求的抛物线上，请充分说明你的判断理由。‎ A B C O D E y x 例三(2009衢州卷)：如图，已知点A(-4，8)和点B(2，n)在抛物线上．‎ ‎　　(1)　求a的值及点B关于x轴对称点P的坐标，并在x轴上找一点Q，使得AQ+QB最短，求出点Q的坐标；‎ ‎　　(2)　平移抛物线，记平移后点A的对应点为A′，点B的对应点为B′，点C(-2，0)和点D(-4，0)是x轴上的两个定点．‎ ‎①　当抛物线向左平移到某个位置时，A′C+CB′ 最短，求此时抛物线的函数解析式；‎ ‎②　当抛物线向左或向右平移时，是否存在某个位置，使四边形A′B′CD的周长最短？若存在，求出此时抛物线的函数解析式；若不存在，请说明理由．‎ ‎4‎ x ‎2‎ ‎2‎ A ‎8‎ ‎-2‎ O ‎-2‎ ‎-4‎ y ‎6‎ B C D ‎-4‎ ‎4‎ 课后练习：‎ ‎1、如图，在边长为1的等边三角形ABC中，点D是AC的中点，点P是BC边的中垂线MN上任一点，则PC＋PD的最小值为 ．‎ 第16题图 第14题图 D A B C P M N ‎2、如图，菱形ABCD的两条对角线分别长6和8，点P是对角线AC上的一个动点，点M、N分别是边AB、BC的中点，则PM+PN的最小值是_____________．‎ ‎3、先阅读下面材料，然后解答问题：（本小题满分10分）‎ ‎【材料一】：如图⑴，直线l上有、两个点，若在直线l上要确定一点P，且使点P到点、的距离之和最小，很明显点P的位置可取在和之间的任何地方，此时距离之和为到的距离. ‎ 如图⑵，直线l上依次有、、三个点，若在直线l上要确定一点P，且使点P到点、、的距离之和最小，不难判断，点P的位置应取在点处，此时距离之和为到的距离. (想一想，这是为什么？)‎ 不难知道，如果直线l上依次有、、、四个点，同样要确定一点P，使它到各点的距离之和最小，则点P应取在点和之间的任何地方；如果直线l上依次有、、、、五个点，则相应点P的位置应取在点的位置. ‎ 图⑴‎ 图⑵‎ ‎【材料二】：数轴上任意两点a、b之间的距离可以表示为. ‎ ‎【问题一】：若已知直线l上依次有点、、、……、共25个点，要确定一点P，使它到已知各点的距离之和最小，则点P的位置应取在 ；‎ 若已知直线l上依次有点、、、……、共50个点，要确定一点P，使它到已知各点的距离之和最小，则点P的位置应取在 . ‎ ‎【问题二】：现要求的最小值，‎ 根据问题一的解答思路，可知当x值为 时，上式有最小值为 .‎ ‎4、已知抛物线(a≠0)的顶点在直线上，且过点A(4，0)．‎ ‎⑴求这个抛物线的解析式；‎ ‎⑵设抛物线的顶点为P，是否在抛物线上存在一点B，使四边形OPAB为梯形？若存在，求出点B的坐标；若不存在，请说明理由. ‎ ‎⑶设点C(1，－3)，请在抛物线的对称轴确定一点D，使的值最大，请直接写出点D的坐标. ‎ ‎5、如图11，已知正比例函数和反比例函数的图像都经过点M（－2，），且P（，－2）为双曲线上的一点，Q为坐标平面上一动点，PA垂直于x轴，QB垂直于y轴，垂足分别是A、B． ‎ ‎（1）写出正比例函数和反比例函数的关系式；‎ ‎（2）当点Q在直线MO上运动时，直线MO上是否存在这样的点Q，使得△OBQ与△OAP面积相等？如果存在，请求出点的坐标，如果不存在，请说明理由； ‎ ‎（3）如图12，当点Q在第一象限中的双曲线上运动时，作以OP、OQ为邻边的平行四边形OPCQ，求平行四边形OPCQ周长的最小值．‎ 图12‎ 图11‎ ‎ ‎ ‎ ‎