2008年庆阳市中考数学试题(含答案) 11页

‎2008年庆阳市中考数学试题 友情提示：‎ ‎1、抛物线的顶点坐标是．‎ ‎2、扇形面积公式为：S扇形=；其中，n为扇形圆心角度数，R为扇形所在圆半径．‎ ‎3、圆锥侧面积公式：S侧=；其中，r为圆锥底面圆半径，为母线长．‎ 一、选择题：本大题共10小题，每小题3分，共30分．每小题给出的四个选项中，只有一项是符合题目要求的，将此选项的代号填入题后的括号内．‎ ‎1． 化简：=（　　）‎ A．8 B．‎-8 ‎ C．-4 D．4‎ ‎2． 下面四张扑克牌中，图案属于中心对称的是图1中的（　　）‎ Ａ．‎ Ｂ．‎ Ｃ．‎ Ｄ．‎ 图1‎ ‎3． 两圆半径分别为3和4，圆心距为7，则这两个圆( )‎ Ａ．外切 Ｂ．相交 Ｃ．相离 Ｄ．内切 ‎4． 下列说法中，正确的是（　　）‎ Ａ．买一张电影票，座位号一定是偶数 Ｂ．投掷一枚均匀的一元硬币，有国徽的一面一定朝上 Ｃ．三条任意长的线段都可以组成一个三角形 Ｄ．从1、2、3这三个数字中任取一个数，取得奇数的可能性大 A B O 图2‎ ‎5．正方形网格中，如图2放置，则=（　　）‎ Ａ． Ｂ．‎ Ｃ． Ｄ．‎ ‎6． 在一个不透明的口袋中，装有若干个除颜色不同其余都相同的球，如果口袋中装有4个红球且摸到红球的概率为，那么口袋中球的总数为（　　）‎ Ａ．12个 Ｂ．9个 Ｃ．6个 Ｄ．3个 ‎7． 如图3，身高为米的某学生想测量学校旗杆的高度，当他站在处时，他头顶端的影子正好与旗杆顶端的影子重合，并测得AC=‎2米，BC=‎8米，则旗杆的高度是（　　）‎ 图3‎ Ａ．米 Ｂ．‎‎7米 Ｃ．‎‎8米 Ｄ．‎9米 ‎ ‎8． 某商品经过两次连续降价，每件售价由原来的55元降到了35元．设平均每次降价的百分率为x，则下列方程中正确的是（　　）‎ A．55 (1+x)2=35 B．35(1+x)2=55‎ 图4‎ C D A O B E C．55 (1－x)2=35 D．35(1－x)2=55‎ ‎9． 如图4，是的直径，为弦，于，则下列结论中不成立的是（ 　）‎ Ａ． Ｂ．‎ Ｃ． Ｄ．‎ ‎10． 若，则由表格中信息可知与之间的函数关系式是（　　）‎ Ａ． Ｂ．‎ Ｃ． Ｄ．‎ 二、填空题：本大题共10小题，每小题4分，共40分．把答案填在题中的横线上．‎ ‎11． 方程的解是 ．‎ ‎12． 要使在实数范围内有意义，应满足的条件是 ．‎ ‎13． “明天下雨的概率为‎0.99”‎是　 事件．‎ ‎14． 二次函数的最小值是 ．‎ ‎15．当物体的某个面平行于投影面时，这个面的正投影与这个面的形状、大小 ‎ ‎（填 “相同”、“不一定相同”、“不相同”之一）．‎ ‎16． 两个相似三角形的面积比S1:S2与它们对应高之比h1:h2之间的关系为　　 　 　．‎ 图6‎ ‎17．如图5，一架梯子斜靠在墙上，若梯子底端到墙的距离=‎3米，，则梯子长AB = 米．‎ A B C 图5‎ ‎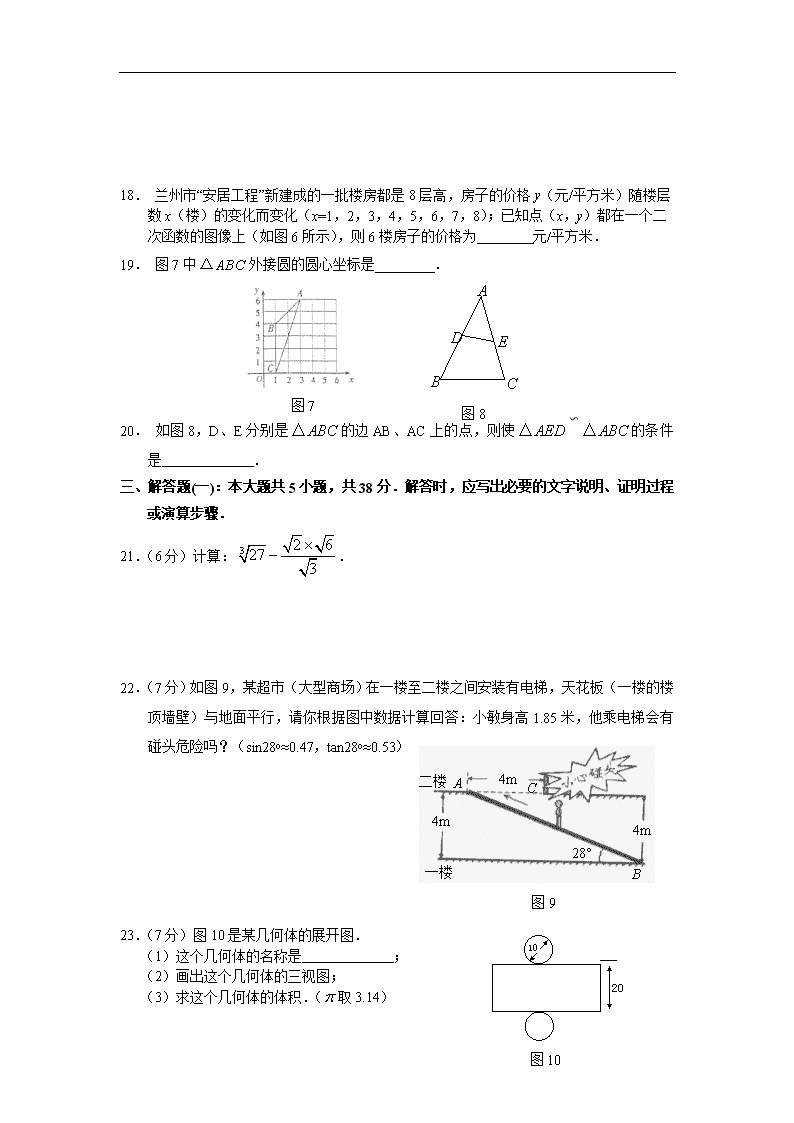18． 兰州市“安居工程”新建成的一批楼房都是8层高，房子的价格y（元/平方米）随楼层数x（楼）的变化而变化（x=1，2，3，4，5，6，7，8）；已知点（x，y）都在一个二次函数的图像上（如图6所示），则6楼房子的价格为 元/平方米．‎ 图7‎ 图8‎ ‎19． 图7中外接圆的圆心坐标是　　　 　．‎ ‎20． 如图8，D、E分别是的边AB、AC上的点，则使∽的条件是 ．‎ 三、解答题(一)：本大题共5小题，共38分．解答时，应写出必要的文字说明、证明过程或演算步骤．‎ ‎21．（6分）计算：．‎ ‎22．（7分）如图9，某超市（大型商场）在一楼至二楼之间安装有电梯，天花板（一楼的楼顶墙壁）与地面平行，请你根据图中数据计算回答：小敏身高‎1.85米，他乘电梯会有碰头危险吗？（sin28o≈0.47，tan28o≈0.53）‎ 二楼 一楼 ‎4m A ‎4m ‎4m B ‎28°‎ C 图9‎ ‎20‎ ‎10‎ 图10‎ ‎23．（7分）图10是某几何体的展开图．‎ ‎ （1）这个几何体的名称是 ；‎ ‎ （2）画出这个几何体的三视图；‎ ‎ （3）求这个几何体的体积．（取3.14）‎ 图11‎ ‎24．（8分）在如图11的方格纸中，每个小方格都是边长为1个单位的正方形，的三个顶点都在格点上（每个小方格的顶点叫格点）．‎ ‎(1) 画出绕点顺时针旋转后的；‎ ‎（2）求点旋转到所经过的路线长． ‎ ‎25．（10分）如图12，线段与相切于点，连结、，OB交于点D，已知，． ‎ D 图12‎ 求：（1）的半径；（2）图中阴影部分的面积．‎ 四、解答题(二)：本大题共4小题，共42分．解答时，应写出必要的文字说明、证明过程或演算步骤．‎ ‎26． （10分）如图13，张大叔从市场上买回一块矩形铁皮，他将此矩形铁皮的四个角各剪去一个边长为‎1米的正方形后，剩下的部分刚好能围成一个容积为‎15米的无盖长方体箱子，且此长方体箱子的底面长比宽多‎2米，现已知购买这种铁皮每平方米需20元钱，问张大叔购回这张矩形铁皮共花了多少元钱？‎ ‎1米 ‎1米 图13‎ ‎27．（10分）图14（1）是夹文件用的铁（塑料）夹子在常态下的侧面示意图．‎ 表示铁夹的两个面，点是轴，于．已知，，．‎ 已知文件夹是轴对称图形，试利用图14（2），求图14（1）中两点的距离（）‎ ‎(2)‎ O ‎(1)‎ 图14‎ ‎28． （10分） 甲、乙两超市（大型商场）同时开业，为了吸引顾客，都举行有奖酬宾活动：凡购物满100元，均可得到一次摸奖的机会．在一个纸盒里装有2个红球和2个白球，除颜色外其它都相同，摸奖者一次从中摸出两个球，根据球的颜色决定送礼金券（在他们超市使用时，与人民币等值）的多少（如下表）．‎ 甲超市:‎ 球 两红 一红一白 两白 礼金券（元）‎ ‎5‎ ‎10‎ ‎5‎ 乙超市:‎ 球 两红 一红一白 两白 礼金券（元）‎ ‎10‎ ‎5‎ ‎10‎ ‎（1）用树状图表示得到一次摸奖机会时中礼金券的所有情况；‎ ‎（2）如果只考虑中奖因素，你将会选择去哪个超市购物？请说明理由．‎ ‎29． （12分）一条抛物线经过点与．‎ ‎（1）求这条抛物线的解析式，并写出它的顶点坐标；‎ ‎（2）现有一半径为1、圆心在抛物线上运动的动圆，当与坐标轴相切时，求圆心的坐标；‎ O 图15‎ ‎（3）能与两坐标轴都相切吗？如果不能，试通过上下平移抛物线使与两坐标轴都相切（要说明平移方法）．‎ 附加题：15分 ‎1．（6分）如图16，在Rt⊿ABC中，BC、AC、AB三边的长分别为a、b、c，则 ‎ sinA=， cosA=，tanA=．‎ b A C B c a 图16‎ ‎ 我们不难发现：sin260o+cos260o=1，… 试探求sinA、cosA、tanA之间存在的一般关系，并说明理由．‎ ‎2．（9分）对于本试卷第19题：“图7中外接圆的圆心坐标是　　 　　．”‎ 请再求：（1) 该圆圆心到弦AC的距离；‎ ‎（2）以BC为旋转轴，将旋转一周所得几何体的全面积（所有表面面积之和）．‎ 图7‎ 参考答案 一、选择题：本大题共10小题，每小题3分，共30分．‎ ‎1．D 2．B 3．A 4．D 5．B 6． A 7． C 8． C 9．C 10． A 二、填空题：本大题共10小题，每小题4分，共40分．‎ ‎11． 0或4 12． 13． 不确定, 或随机 14． 4 15． 相同 ‎16． 17．4 18． 2080 19． ‎ ‎20． ，或，或 三、解答题（一）：本大题共5小题，共38分．‎ ‎21． 本小题满分6分 原式=3-2 5分 ‎　　　 =1． 6分 ‎22．本小题满分7分 作交于，则， 3分 在中， 5分 ‎（米）． 6分 所以,小敏不会有碰头危险． 7分 ‎23．本小题满分7分 ‎（1）圆柱； 2分 ‎（2）三视图为：‎ ‎ 5分 ‎（3）体积为:==1570． 7分 B1‎ A1‎ C1‎ ‎24．本小题满分8分 ‎（1）如图：‎ ‎ 3分 ‎（2） ∵ 点旋转到所经过的路线长为以OA为半径圆的周长的， 5分 ‎∴ 点旋转到所经过的路线长为×2=×=． 8分 D ‎25． 本小题满分10分 ‎（1）连结． 1分 则 ． 2分 又，‎ ‎∴． 3分 在中，．‎ ‎∴ 的半径为． 5分 ‎（2） ∵ OC=, ∴ ∠B=30o, ∠COD=60o． 7分 ‎∴ 扇形OCD的面积为=． 8分 ‎∴ 阴影部分的面积为-=- （cm2）． 10分 四、解答题（二）：本大题共4小题，共42分．‎ ‎26． 本小题满分10分 设这种箱子底部宽为米，则长为米， 2分 依题意，得． 5分 解得（舍），． 7分 ‎∴ 这种箱子底部长为米、宽为米．‎ 由长方体展开图知，要购买矩形铁皮面积为（米）． 9分 ‎∴ 做一个这样的箱子要花元钱． 10分 ‎27．本小题满分10分 解：如图，连结AB与CO延长线交于E， 1分 ‎∵ 夹子是轴对称图形，对称轴是CE，A、B为一组对称点，‎ ‎∴ CE⊥AB，AE=EB． 3分 在、中，‎ ‎∵ ∠ACE=∠OCD，∠OCD公用,‎ ‎∴ ∽． 5分 ‎∴ ．‎ 又 OC==26, 8分 ‎∴ AE==‎ ‎∴ AB=2AE=30（mm）． 10分 ‎28． 本小题满分10分 开始 第1个球 红 白 第2个球 红 白 白 红 红 白 ‎（1）树状图为：‎ ‎… 4分 ‎（2）方法1：‎ ‎∵ 去甲超市购物摸一次奖获10元礼金券的概率是（甲）， 7分 去乙超市购物摸一次奖获10元礼金券的概率是（乙）， 9分 ‎ ∴ 我选择去甲超市购物． 10分 ‎ 方法2：‎ ‎∵ 两红的概率P=，两白的概率P=，一红一白的概率P==， 6分 ‎∴ 在甲商场获礼金券的平均收益是：×5+×10+×5=； 8分 在乙商场获礼金券的平均收益是：×10+×5+×10=．‎ ‎∴ 我选择到甲商场购物． 10分 说明：树状图表示为如下形式且按此求解第（2）问的，也正确．‎ ‎29． 本小题满分12分 ‎（1）∵ 抛物线过两点， ‎ ‎∴ 1分 解得 2分 ‎　　∴ 抛物线的解析式是，顶点坐标为． 3分 ‎　　（2）设点的坐标为，‎ ‎　　当与轴相切时，有，∴． 5分 由，得；‎ 由，得．‎ ‎　　此时，点的坐标为． 6分 ‎　　当与轴相切时，有，∴ ． 7分 ‎　　由，得，解得；‎ ‎　　由，得，解得．‎ 此时，点的坐标为，． 9分 综上所述，圆心的坐标为：，，．‎ 注：不写最后一步不扣分．‎ ‎（3） 由（2）知，不能． 10分 设抛物线上下平移后的解析式为,‎ 若能与两坐标轴都相切，则,‎ 即x0=y0=1；或x0=y0=-1；或x0=1，y0=-1；或x0=-1，y0=1． 11分 取x0=y0=1，代入，得h=1．‎ ‎∴ 只需将向上平移1个单位，就可使与两坐标轴都相切．‎ ‎ 12分 附加题：15分 ‎1．存在的一般关系有：‎ ‎（1） sin‎2A+cos‎2A=1；‎ ‎（2）tanA=． 2分 b A C B c a ‎（1） 证明：∵ sinA=, cosA=, ‎ a2+b2=c2, 3分 ‎∴ sin‎2A+cos‎2A==1． 4分 ‎（2） 证明：∵ sinA=, cosA=, ‎ ‎∴ tanA== 5分 ‎=． 6分 ‎2．（1）‎ 方法1：‎ 如图，圆心为P（5，2），作PD⊥AC于D，则AD=CD． 1分 D P 连结CP，∵ AC为是为6、宽为2的矩形的对角线，‎ ‎∴ AC==2． 2分 同理 CP==2． 3分 ‎∴ PD==． 4分 方法2：‎ ‎∵ 圆心为P（5，2），作PD⊥AC于D，则AD=CD． 1分 由直观，发现点D的坐标为（2，3）． 2分 又∵ PD为是为3、宽为1的矩形的对角线，‎ ‎∴ PD==． 4分 ‎ （2）‎ ‎∵ 旋转后得到的几何体是一个以2为底面圆半径、6为高的大圆锥，再挖掉一个以2为底面圆半径、2为高的小圆锥， 5分 又 它们的母线之长分别为小==，大==， 7分 ‎∴ 所求的全面积为：大+小 8分 ‎ =（大+小）‎ ‎=4（-）． 9分 说明：对于以上各解答题学生试卷中出现的不同解法，请参考本标准给分．‎