- 393.00 KB
- 2021-05-13 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
2016专题:探索规律
规律探索问题通常考查数的变化规律,然后用代数式表示这一规律,或者根据规律求出相应的数值.解题时,要通过观察、猜想、验证等步骤,应使所得到的规律具有普遍性,只有这样才能应用与解题.
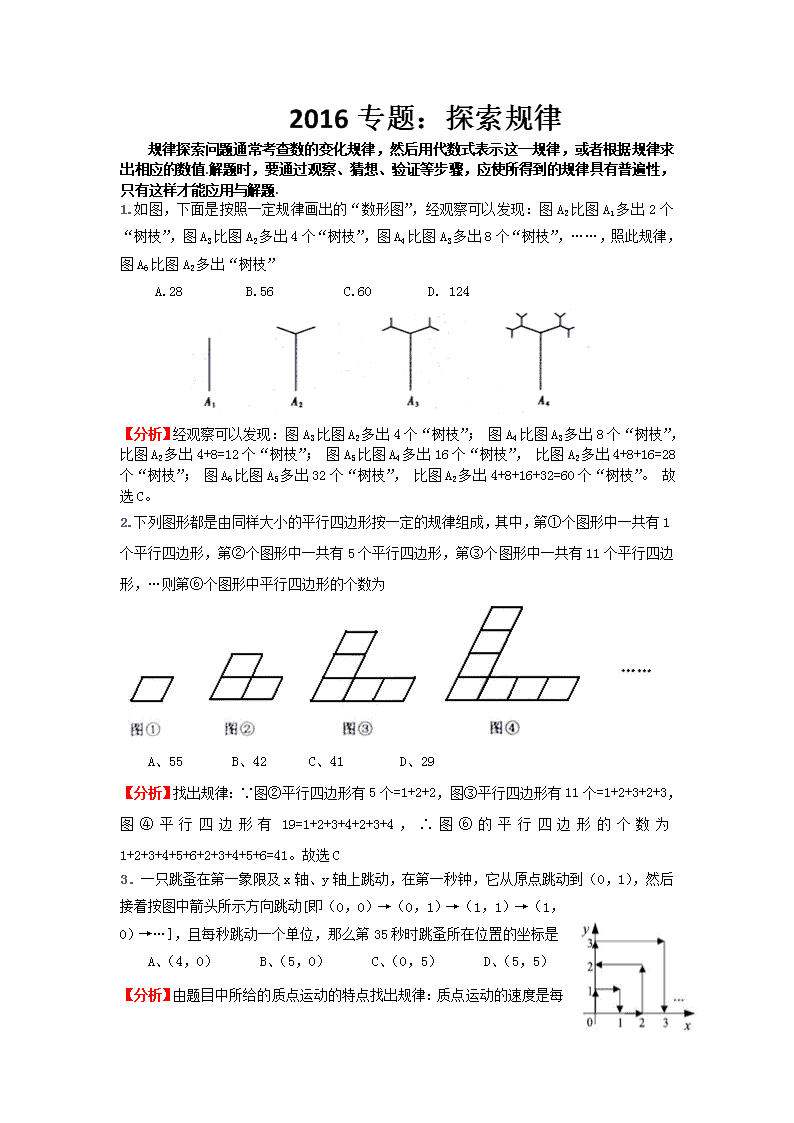
1.如图,下面是按照一定规律画出的“数形图”,经观察可以发现:图A2比图A1多出2个“树枝”, 图A3比图A2多出4个“树枝”, 图A4比图A3多出8个“树枝”,……,照此规律,图A6比图A2多出“树枝”
A.28 B.56 C.60 D. 124
【分析】经观察可以发现:图A3比图A2多出4个“树枝”; 图A4比图A3多出8个“树枝”, 比图A2多出4+8=12个“树枝”; 图A5比图A4多出16个“树枝”, 比图A2多出4+8+16=28个“树枝”; 图A6比图A5多出32个“树枝”, 比图A2多出4+8+16+32=60个“树枝”。 故选C。
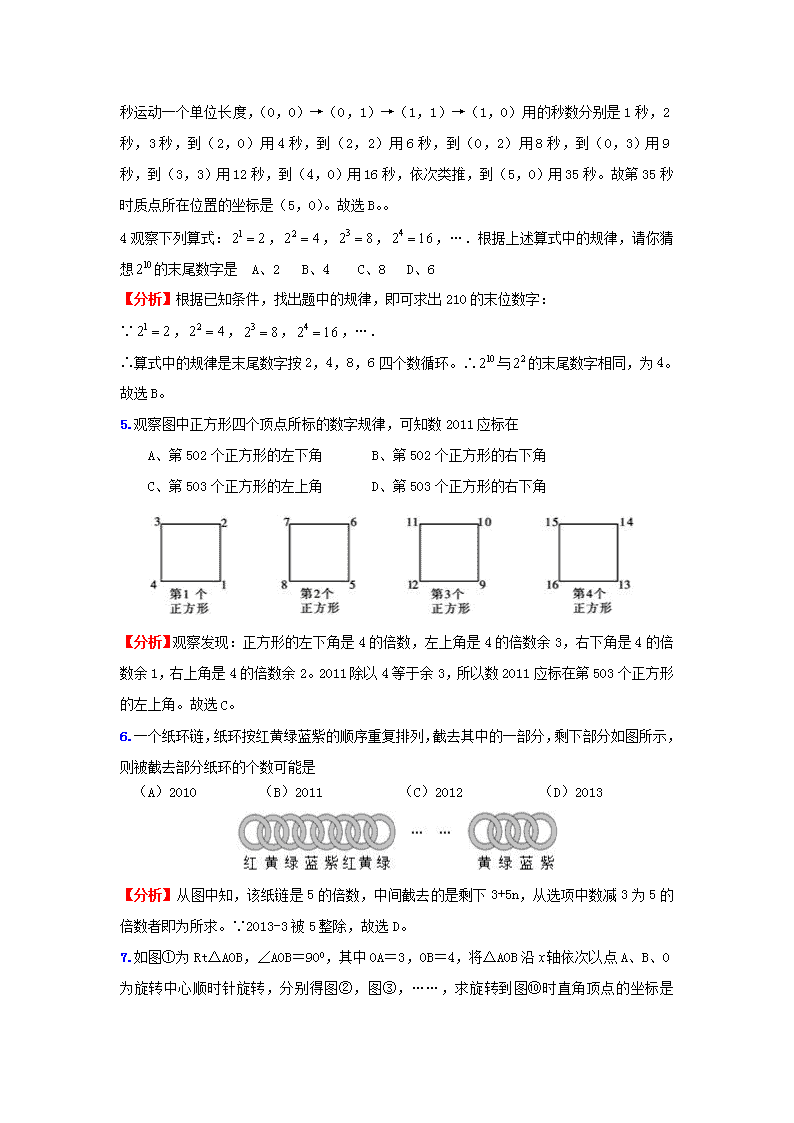
2.下列图形都是由同样大小的平行四边形按一定的规律组成,其中,第①个图形中一共有1个平行四边形,第②个图形中一共有5个平行四边形,第③个图形中一共有11个平行四边形,…则第⑥个图形中平行四边形的个数为
A、55 B、42 C、41 D、29
【分析】找出规律:∵图②平行四边形有5个=1+2+2,图③平行四边形有11个=1+2+3+2+3,图④平行四边形有19=1+2+3+4+2+3+4,∴图⑥的平行四边形的个数为1+2+3+4+5+6+2+3+4+5+6=41。故选C
3.一只跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟,它从原点跳动到(0,1),然后接着按图中箭头所示方向跳动[即(0,0)→(0,1)→(1,1)→(1,0)→…],且每秒跳动一个单位,那么第35秒时跳蚤所在位置的坐标是
A、(4,O) B、(5,0) C、(0,5) D、(5,5)
【分析】
由题目中所给的质点运动的特点找出规律:质点运动的速度是每秒运动一个单位长度,(0,0)→(0,1)→(1,1)→(1,0)用的秒数分别是1秒,2秒,3秒,到(2,0)用4秒,到(2,2)用6秒,到(0,2)用8秒,到(0,3)用9秒,到(3,3)用12秒,到(4,0)用16秒,依次类推,到(5,0)用35秒。故第35秒时质点所在位置的坐标是(5,0)。故选B。。
4观察下列算式:,,,,….根据上述算式中的规律,请你猜想的末尾数字是 A、2 B、4 C、8 D、6
【分析】根据已知条件,找出题中的规律,即可求出210的末位数字:
∵,,,,….
∴算式中的规律是末尾数字按2,4,8,6四个数循环。∴与的末尾数字相同,为4。故选B。
5.观察图中正方形四个顶点所标的数字规律,可知数2011应标在
A、第502个正方形的左下角 B、第502个正方形的右下角
C、第503个正方形的左上角 D、第503个正方形的右下角
【分析】观察发现:正方形的左下角是4的倍数,左上角是4的倍数余3,右下角是4的倍数余1,右上角是4的倍数余2。2011除以4等于余3,所以数2011应标在第503个正方形的左上角。故选C。
6.一个纸环链,纸环按红黄绿蓝紫的顺序重复排列,截去其中的一部分,剩下部分如图所示,则被截去部分纸环的个数可能是
(A)2010 (B)2011 (C)2012 (D)2013
【分析】从图中知,该纸链是5的倍数,中间截去的是剩下3+5n,从选项中数减3为5的倍数者即为所求。∵2013-3被5整除,故选D。
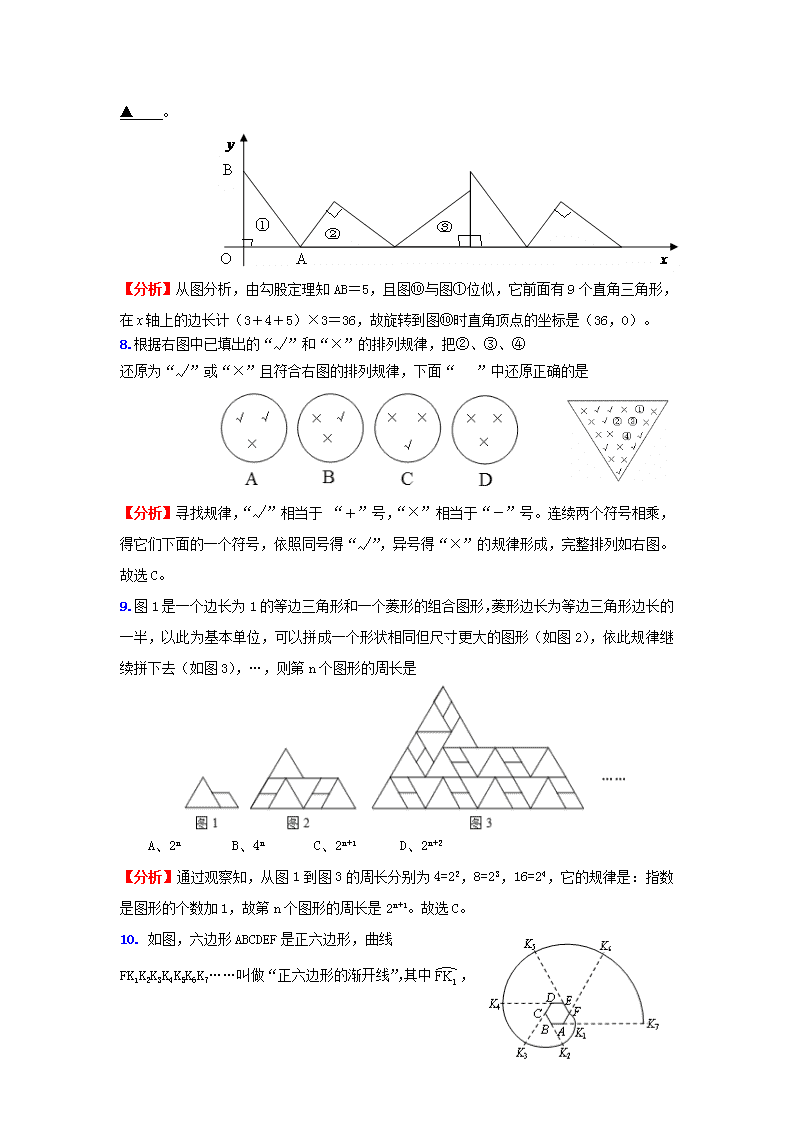
7.如图①为Rt△AOB,∠AOB=900,其中OA=3,OB=4,将△AOB沿轴依次以点A、B、O为旋转中心顺时针旋转,分别得图②,图③,……,求旋转到图⑩时直角顶点的坐标是
▲ 。
【分析】从图分析,由勾股定理知AB=5,且图⑩与图①位似,它前面有9个直角三角形,在轴上的边长计(3+4+5)×3=36,故旋转到图⑩时直角顶点的坐标是(36,0)。
8.根据右图中已填出的“√”和“×”的排列规律,把②、③、④
还原为“√”或“×”且符合右图的排列规律,下面“ ”中还原正确的是
【分析】寻找规律,“√”相当于 “+”号,“×”相当于“-”号。连续两个符号相乘,得它们下面的一个符号,依照同号得“√”,异号得“×”的规律形成,完整排列如右图。故选C。
9.图1是一个边长为1的等边三角形和一个菱形的组合图形,菱形边长为等边三角形边长的一半,以此为基本单位,可以拼成一个形状相同但尺寸更大的图形(如图2),依此规律继续拼下去(如图3),…,则第n个图形的周长是
A、2n B、4n C、2n+1 D、2n+2
【分析】通过观察知,从图1到图3的周长分别为4=22,8=23,16=24,它的规律是:指数是图形的个数加1,故第n个图形的周长是2n+1。故选C。
10. 如图,六边形ABCDEF是正六边形,曲线FK1K2K3K4K5K6K7……叫做“正六边形的渐开线”,其中,
,,,,,……的圆心依次按点A,B,C,D,E,F循环,其弧长分别记为l1,l2,l3,l4,l5,l6,…….当AB=1时,l2 011等于
A. B. C. D.
【分析】找出规律:每段弧的度数都等于60°,的半径为n,所以l2 011==。故选B。
11.如图,用围棋子按下面的规律摆图
形,则摆第n个图形需要围棋子的枚数为
A.5n B.5n-1
C.6n-1 D.2n2+1
【分析】从所给的图形找出规律,所摆图形的特点:下面部分是一个用棋子围成的一个正方形,它需要围棋子的枚数分别为4,8,12,…4 n;上面部分围棋子的枚数分别为1,3,5,…2 n-1。从而摆第n个图形需要围棋子的枚数为4 n+2 n-1=6n-1。故选C。
12.如图,以边长为1的正方形ABCD的边AB为对角线作
第二个正方形AEBO1,再以BE为对角线作第三个正方形EFBO2,如此作下去,…,则所作的第n个正方形的面积Sn= ▲ .
【分析】找出规律:第1个正方形的边长为1,面积S1=1;第2个正方形的边长为,面积S2=;第3个正方形的边长为,面积S3=;第4个正方形的边长为,面积S4=;…,则第n个正方形的面积Sn=。
13.观察下列各图形中小正方形的个数,依此规律,第11个图形中小正方形的个数为
(1)
(2)
(3)
(4)
(5)
A.78 B.66 C.55 D.50
【分析】由题意得:第一个图形中小正方形的个数为1,第二个为1+2=3,第三个为1+2+3=6,第四个为1+2+3+4=10, …;第(11)个图形中小正方形的个数为:1+2+3+4+5+6+7+8+9+10+11=66。故选B。
14.根据图中数字的规律,在最后一个空格中填上适当的数字 ▲ 。
【分析】观察图中的数字得出框中右下角的数字特点为:上方数字与左下角数字的乘积再加上上方数字的和。故最后一个空格中填上适当的数字为9×81+9=738。
15.填在下面各正方形中的四个数之间都有相同的规律,根据这种规律,m的值是 ▲ .
【分析】分析前三个正方形可知,规律为右上和左下两个数的积减左上的数等于右下的数,且左上,左下,右上三个数是相邻的偶数.因此,图中阴影部分的两个数分别是左下是12,右上是14。则m=12×14﹣10=158。
16.(广西贺州3分)如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到
点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),……,按这样的运动规律,经过第2011
次运动后,动点P的坐标是_ ▲ .
【分析】由已知找出规律:运动的点P的横坐标等于它运动的次数;它的纵坐标根据运动次数的奇偶性确定,奇数次时纵坐标为2,偶奇数次时纵坐标为0。按这样的运动规律,经过第2011次运动后,动点P的坐标是(2011,2)。
17.通过找出这组图形符号中所蕴含的内在规律,在空白处的横线上填上恰当的图形.
【分析】观察图形,发现规律:(1)这几幅图是A、B、C、D、E、F六个字母的对称图形;(2)1、3、5是上下对称;2、4、6是左右对称.根据此规律即可得到图形。
18.如图,观察由棱长为1的小立方体摆成的图形,寻找规律:如图①中:共有1个小立方体.其中1个看得见,0个看不见;如图②中:共有8个小立方体,其中7个看得见,1个看不 见;如图③中:共有27个小立方体,其中19个看得见,8个看不见;……,则第⑥个图中.看得见的小立方体有 ▲ 个。
【分析】根据几何体的三视图知,三视图看得见的小立方体有6×6+6×5+5×5=91。
19.(济宁3分)如图,观察每一个图中黑色正六边形的排列规律,则第10个图中黑色正六边形有 ▲ 个。
【分析】观察每一个图中黑色正六边形的排列规律,
第1个图中黑色正六边形有1=12个,第2个图中黑色正六边形有4=22个,第3个图中黑色正六边形有9=32个,…则第10个图中黑色正六边形有102=100个。
20.如图,上面各图都是用全等的等边三角形拼成的一组图形.则在第10个这样的图形中共有 ▲ 个等腰梯形.
【分析】观察图形可知第10个图形中有21个等边三角形,按照从左往右的顺序可得等腰梯形的个数为:10+9+9+8+8+7+7+6+6+5+5+4+4+3+3+2+2+1+1=100。
21.将一些半径相同的小圆按如图所示的规律摆放,请仔细观察,第 n 个图形 有 ▲ 个小圆 · (用含 n 的代数式表示)
第1个图形 第 2 个图形 第3个图形 第 4 个图形
【分析】寻找规律:第1个图形中间有2=1×2个小圆,第2个图形中间有6=2×3个小圆,第3个图形中间有12=3×4个小圆,第4个图形中间有20=4×5个小圆,······第n个图形中间有n(n+1)个小圆。共有4+n(n+1)=个小圆。
22用黑白两种正六边形地面瓷砖按如图所示规律拼成若干图案,则第n个图案中有白色地面瓷砖 ▲ 块。
第1个 第2个 第3个
【分析】根据第1个图形有6块白色地面瓷砖,第2个图形有10块白色瓷砖,每多1个黑色瓷砖则多4块白色瓷砖,根据此规律即可写出第n个图案中的白色瓷砖的块数
第1个图案白色瓷砖的块数是:6,
第2个图案白色瓷砖的块数是:10=6+4,
第3个图案白色瓷砖的块数是:14=6+4×2,
…
以此类推,第n个图案白色瓷砖的块数是:6+4(n-1)=4n+2。
23.先找规律,再填数:
······
则 ▲
【分析】通过观察得:每个算式第一个加数的分母依次是1,3,5,7,…,是首项为1,公差为2的等差数列;每个算式的减数的分母依次是1,2,3,4,…即是第几个算式。设要求的是第n个算式,则依题有:1+(n﹣1)×2=2011,解得:n=1006。
24观察下列等式:
①1=12;②2+3+4=32;③3+4+5+6+7=52;④4+5+6+7+8+9+10=72;…
请你根据观察得到的规律判断下列各式正确的是
A.1005+1006+1007+…+3016=20112 B.1005+1006+1007+…+3017=20112
C.1006+1007+1008+…+3016=20112 D.1007+1008+1009+…+3017=20112
【分析】观察所给等式,找出规律:等式右边幂的底数是左边首尾两个数之和的一半。而四个等式中只有1006+1007+1008+…+3016=20112符合以上规律,故选C。
25.观察一列单项式:,,,,… 根据你发现的规律,第7个单项式为 ▲ ;第个单项式为 ▲ .
【分析】通过观察已知条件,找出这列单项式的规律即可求出结果:根据观察可得,单项式的系数的符号正负相间,奇数项为正,偶数项为负,系数的数值为2的项数减1次方,故系数为; 单项式的指数为项数。因此,第7个单项式为;第个单项式为。
26.如下数表是由从1开始的连续自然数组成,观察规律并完成各题的解答.
1
2 3 4
5 6 7 8 9
10 11 12 13 14 15 16
17 18 19 20 21 22 23 24 25
26 27 28 29 30 31 32 33 34 35 36
…………………………
(1)表中第8行的最后一个数是______________,它是自然数_____________的平方,第8行共有____________个数;
(2)用含n的代数式表示:第n行的第一个数是___________________,最后一个数是________________,第n行共有_______________个数;
(3)求第n行各数之和.
【答案】解:(1)64,8,15。
(2)n2-2n+2,n2,2n-1。
(3)第n行各数之和:。
【分析】(1)(2)由表的构成可以看出:①每一行的最后一个数是:行数的平方。所以第8行的最后一个数是82=64;第n行的最后一个数是n2。②
每一行的第一个数是:前一行最后一个数加1。所以第n行的第一个数是(n-1)2+1=n2-2n+2。③每一行的个数是:最后一个数减去的第一个数加1。所以第n行个数是n2-(n2-2n+2)=2n-1。
(3)每一行各数之和是:这一行的第一个数与最后一个数的平均数剩以这一行的个数。所以第n行各数之和为。
27.在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其行走路线如下图所示.
A1
A2
A3
A4
A5
A6
A7
A8
A9
A10
A11
A12
O
x
y
1
(1)填写下列各点的坐标:A4( , )、A8( , )、A12( , );
(2)写出点A4n的坐标(n是正整数);
(3)指出蚂蚁从点A100到点A101的移动方向.
【答案】解:⑴ 0,1;1,0;6,0。 ⑵A4n(2n,0)。 ⑶向上。
⑵观察规律,点A4、A8、A12、…A4n都在X轴上,它们的横坐标是它们的下标除以2:2、4、6、…2n,故点A4n的坐标为(2n,0)。
(3)由⑵可知,蚂蚁移动的规律是4n一个周期,因此蚂蚁从点A100到点A101的移动方向是向上。
28.如图(1),将一个正六边形各边延长,构成一个正六角星形AFBDCE,它的面积为1;取△ABC和△DEF各边中点,连接成正六角星形A1F1B1D1C1E1,如图(2)中阴影部分;取△A1B1C1和△D1E1F1各边中点,连接成正六角星形A2F2B2D2C2E2,如图(3)中阴影部分;如此下去…,则正六角星形
A4F4B4D4C4E4的面积为______▲______.
(1)
A1
B
C
D
A
F
E
B
C
D
A
F
E
B
C
D
A
F
E
B1
C1
F1
D1
E1
A1
B1
C1
F1
D1
E1
A2
B2
C2
F2
D2
E2
(2)
(3)
【分析】∵正六角星形A2F2B2D2C2E2边长是正六角星形A1F1B1D1C1E边长的,
∴正六角星形A2F2B2D2C2E2面积是正六角星形A1F1B1D1C1E面积的。
同理∵正六角星形A4F4B4D4C4E4边长是正六角星形A1F1B1D1C1E边长的,
∴正六角星形A4F4B4D4C4E4面积是正六角星形A1F1B1D1C1E面积的。
29.如图所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,
则第n (n是大干0的整数)个图形需要黑色棋子的个教是____▲_____.
30.如图,依次以三角形、四边形、…、n边形的各顶点为圆心画半径为l的圆,且圆与圆之间两两不相交.把三角形与各圆重叠部分面积之和记为S3,四边形与各圆重叠部分面积之和记为S4,…。n边形与各圆重叠部分面积之和记为Sn.则S90的值为 ▲ _.(结果保留π)
【答案】。
31.(山东德州4分)长为1,宽为的矩形纸片(),如图那样折一下,剪下一个边长等于矩形宽度的正方形(称为第一次操作);再把剩下的矩形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形(称为第二次操作);如此反复操作下去.若在第n次操作后,剩下的矩形为正方形,则操作终止.当n=3时,的值为 ▲ .
【答案】。