内蒙古鄂尔多斯中考数学试卷 11页

‎2018年内蒙古鄂尔多斯中考数学试卷 ‎（满分120分，考试时间120分钟）‎ 一、单项选择题（本大题共10小题，每题3分，共30分）‎ 1. 在，-2018，，π这四个数中，无理数是（ ）‎ A． B．-2018 C． D．π 2. 下列计算正确的是（ ）‎ A．3x-x=3 B．‎ C．(x-1)2=x2-2x-1 D．(-2a2)3=-6a6‎ 3. 下列函数中，自变量x的取值范围为x＞1的是（ ）‎ A． B． C． D．‎ 4. 以O为中心点的量角器与直角三角板ABC如图摆放，直角顶点B在零刻度线所在直线DE上，且量角器与三角板只有一个公共点P，若 ‎∠EOP=134°50′，则∠CBD的度数是（ ）‎ A．45°10′ B．44°50′ C．46°10′ D．不能确定 5. 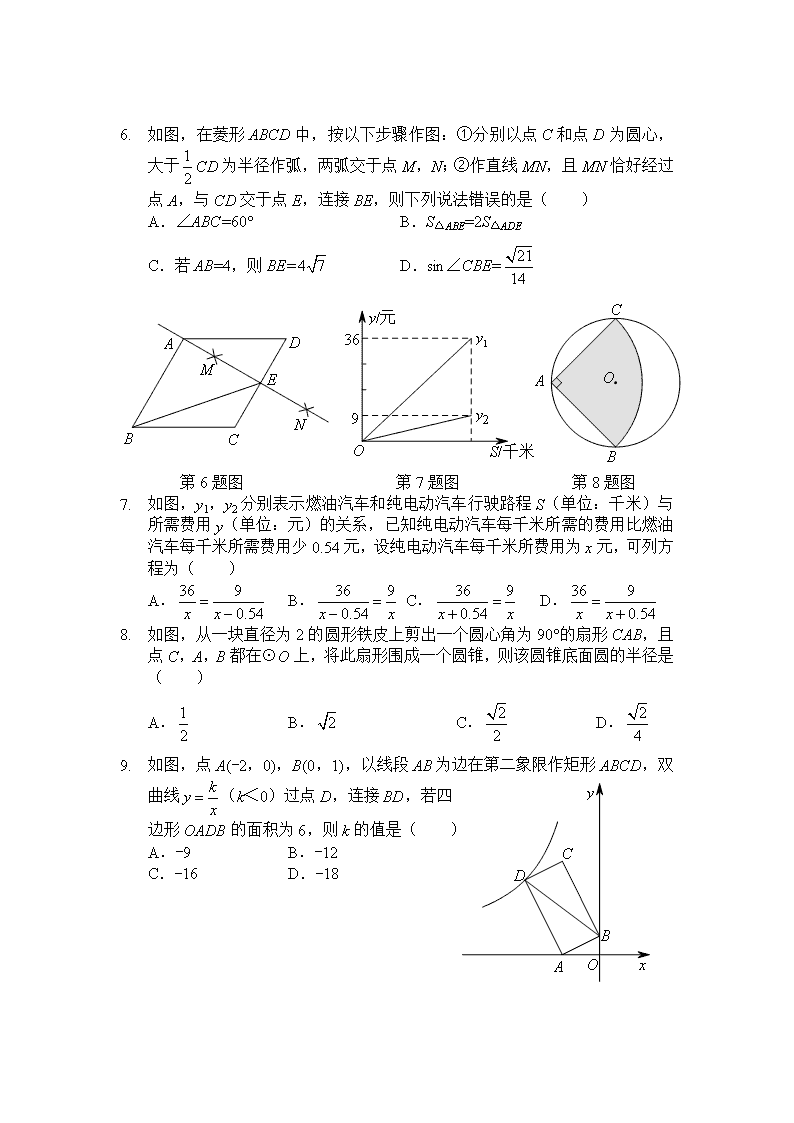为了帮助我市一名贫困学生，某校组织捐款，现从全校所有学生的捐款数额中随机抽取10名学生的捐款数统计如下表：‎ 捐款金额（单位：元）‎ ‎20‎ ‎30‎ ‎50‎ ‎90‎ 人数（单位：个）‎ ‎2‎ ‎4‎ ‎3‎ ‎1‎ 则下列说法正确的是（ ）‎ A．10名学生是总体的一个样本 B．中位数是40‎ C．众数是90‎ D．方差是400‎ 1. 如图，在菱形ABCD中，按以下步骤作图：①分别以点C和点D为圆心，大于CD为半径作弧，两弧交于点M，N；②作直线MN，且MN恰好经过点A，与CD交于点E，连接BE，则下列说法错误的是（ ）‎ A．∠ABC=60° B．S△ABE=2S△ADE C．若AB=4，则BE= D．sin∠CBE=‎ ‎ 第6题图 第7题图 第8题图 2. 如图，y1，y2分别表示燃油汽车和纯电动汽车行驶路程S（单位：千米）与所需费用y（单位：元）的关系，已知纯电动汽车每千米所需的费用比燃油汽车每千米所需费用少0.54元，设纯电动汽车每千米所费用为x元，可列方程为（ ）‎ A． B． C． D．‎ 3. 如图，从一块直径为2的圆形铁皮上剪出一个圆心角为90°的扇形CAB，且点C，A，B都在⊙O上，将此扇形围成一个圆锥，则该圆锥底面圆的半径是（ ）‎ A． B． C． D．‎ 4. 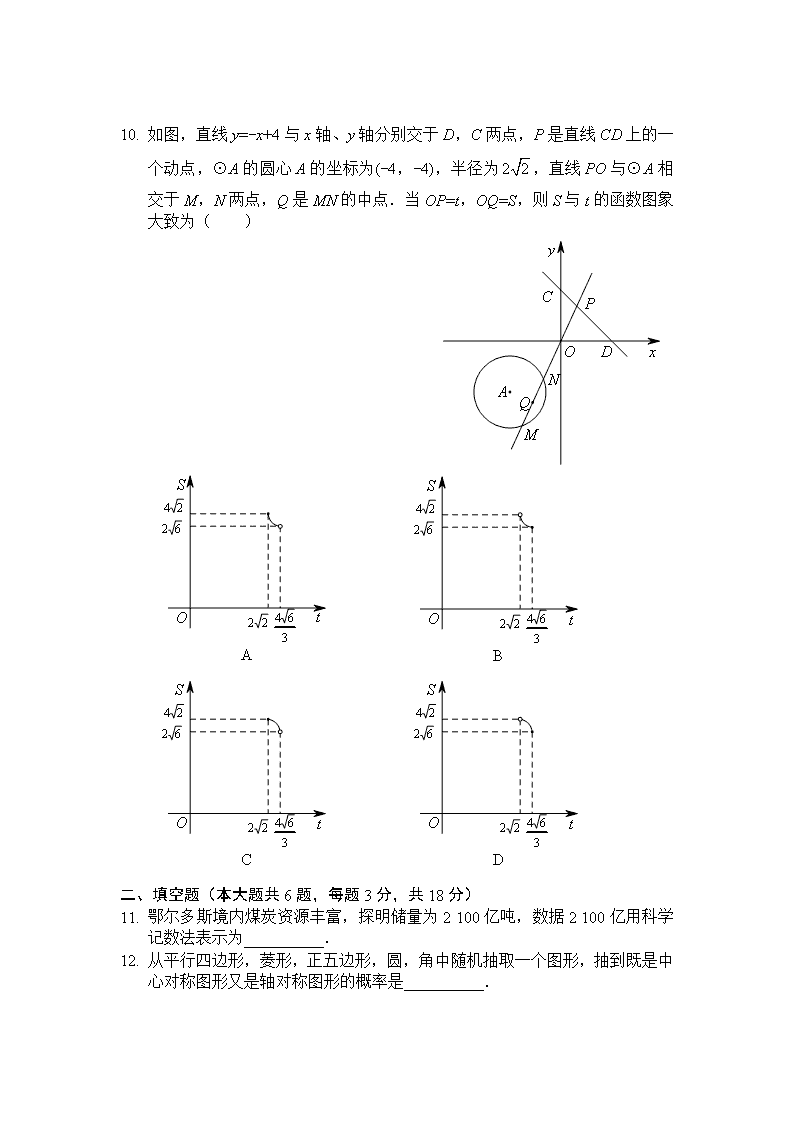如图，点A(-2，0)，B(0，1)，以线段AB为边在第二象限作矩形ABCD，双曲线（k＜0）过点D，连接BD，若四 边形OADB的面积为6，则k的值是（ ）‎ A．-9 B．-12 ‎ C．-16 D．-18‎ 1. 如图，直线y=-x+4与x轴、y轴分别交于D，C两点，P是直线CD上的一个动点，⊙A的圆心A的坐标为(-4，-4)，半径为，直线PO与⊙A相交于M，N两点，Q是MN的中点．当OP=t，OQ=S，则S与t的函数图象大致为（ ）‎ ‎ ‎ ‎ ‎ 二、填空题（本大题共6题，每题3分，共18分）‎ 2. 鄂尔多斯境内煤炭资源丰富，探明储量为2 100亿吨，数据2 100亿用科学记数法表示为__________．‎ 3. 从平行四边形，菱形，正五边形，圆，角中随机抽取一个图形，抽到既是中心对称图形又是轴对称图形的概率是__________．‎ 1. 下列说法正确的是__________．‎ ‎①在同一平面内，a，b，c为直线，若a⊥b，b⊥c，则a∥c．‎ ‎②若ac＞bc，则a＞b的逆命题是真命题．‎ ‎③若M(a，2)，N(1，b)关于x轴对称，则a+b=-1．‎ ‎④一个多边形的边数增加1条时，内角和增加180°，外角和不变．‎ ‎⑤的整数部分是a，小数部分是b，则ab=．‎ 2. 在平面直角坐标系中，对于点P(a，b)，我们把Q(-b+1，a+1)叫做点P的伴随点，已知A1的伴随点为A2，A2的伴随点为A3，…，这样依次下去得到A1，A2，A3，…，An，若A1的坐标为(3，1)，则A2018的坐标为_____________．‎ 3. 如图是一个边长为4的正方形，长为4的线段PQ的两端在正方形相邻的两边上滑动，且点P沿A→B→C→D滑动到点D终止，在整个滑动过程中，PQ的中点R所经过的路线长为__________．‎ 4. 如图1，AF，BE是△ABC的中线，AF⊥BE，垂足为点P，设BC=a，AC=b，AB=c，则a2+b2=5c2，利用这一性质计算．如图2，在□ABCD中，E，F，G分别是AD，BC，CD的中点，EB⊥EG于点E，AD=8，AB=，则AF=_______．‎ ‎ ‎ 三、解答题（本大题共8题，72分）‎ 1. ‎（8分）‎ ‎（1）化简求值：，其中x=-22+2sin45°+|-3|；‎ ‎（2）解不等式组：，并求其非负整数解．‎ 2. ‎（8分）“金山银山，不如绿水青山”．鄂尔多斯市某旗区不断推进“森林城市”建设，今春种植四类树苗，园林部门从种植的这批树苗中随机抽取了4 000棵，将各类树苗的种植棵数绘制成扇形统计图，将各类树苗的成活棵数绘制成条形统计图，经统计松树和杨树的成活率较高，且杨树的成活率为97%．根据图表中的信息解答下列问题：‎ ‎（1）扇形统计图中松树所对的圆心角为_______度，并补全条形统计图．‎ ‎（2）该旗区今年共种树32万棵，成活了约多少棵？‎ ‎（3）园林部门决定明年从这四类树苗中选两类种植，请用列表法或树状图求恰好选到成活率较高的两类树苗的概率．（松树、杨树、榆树、柳树分别用A，B，C，D表示）‎ 1. ‎（8分）如图，在△ABC中，∠BAC=45°，AD⊥BC于点D，BD=6，DC=4，求AD的长．‎ 小明同学利用翻折，巧妙地解答了此题，按小明的思路探究并解答下列问题：‎ ‎（1）分别以AB，AC为对称轴，画出△ABD和△ACD的对称图形，点D的对称点分别为点E，F，延长EB和FC相交于点G，求证：四边形AEGF是正方形；‎ ‎（2）设AD=x，建立关于x的方程模型，求出AD的长．‎ 1. ‎（8分）王阿姨家的阳台上放置了一个晾衣架，完全稳固张开如图1．图2，3是晾衣架的侧面展开图，△AOB是边长为130 cm的等边三角形，晾衣架OE，OF能以O为圆心转动，且OE=OF=130 cm：在OA，OB上的点C，D处分别有支撑杆CN，DM能以C，D为圆心转动．‎ ‎（1）如图2，若EF平行于地面AB，王阿姨的衣服穿在衣架上的总长度是110 cm，垂挂在晾衣杆OE上是否会拖到地面上？说明理由．‎ ‎（2）如图3，当支撑杆DM支到点M′，此时∠EOB=78°，点E离地面距离最大．保证衣服不拖到地面上，衣服穿在衣架上的总长度最长约为多少厘米？（结果取整）‎ 参考数据：（≈，sin78°≈，cos78°≈，sin18°≈，cos18°≈）‎ 1. ‎（8分）如图，⊙O是△ABC的外接圆，AC是直径，弦BD=BA，EB⊥DC，交DC的延长线于点E．‎ ‎（1）求证：BE是⊙O的切线；‎ ‎（2）当sin∠BCE=，AB=3时，求AD的长．‎ 2. ‎（9分）牧民巴特尔在生产和销售某种奶食品时，采取客户先网上订购，然后由巴特尔付费选择甲或乙快递公司送货上门的销售方式，甲快递公司运送2千克，乙快递公司运送3千克共需运费42元：甲快递公司运送5千克，乙快递公司运送4千克共需运费70元．‎ ‎（1）求甲、乙两个快递公司每千克的运费各是多少元？‎ ‎（2）假设巴特尔生产的奶食品当日可以全部出售，且选择运费低的快递公司运送，若该产品每千克的生产成本y1元（不含快递运费），销售价y2元与生产量x千克之间的函数关系式为：，‎ y2=-6x+120（0＜x＜13），则巴特尔每天生产量为多少千克时获得利润最大？最大利润为多少元？‎ 1. ‎（11分）如图，直线与x轴、y轴分别交于点B，C，抛物线过B，C两点，且与x轴的另一个交点为点A，连接AC．‎ ‎（1）求抛物线的解析式；‎ ‎（2）在抛物线上是否存在点D（与点A不重合），使得S△DBC=S△ABC，若存在，求出点D的坐标；若不存在，请说明理由；‎ ‎（3）有宽度为2，长度足够长的矩形（阴影部分）沿x轴方向平移，与y轴平行的一组对边交抛物线于点P和点Q，交直线CB于点M和点N，在矩形平移过程中，当以点P，Q，M，N为顶点的四边形是平行四边形时，求点M的坐标．‎ 1. ‎（12分）‎ ‎（1）【操作发现】‎ 如图1，将△ABC绕点A顺时针旋转60°，得到△ADE，连接BD，则 ‎∠ABD=________度．‎ ‎ ‎ ‎（2）【类比探究】‎ 如图2，在等边三角形ABC内任取一点P，连接PA，PB，PC，求证：以PA，PB，PC的长为三边必能组成三角形．‎ ‎（3）【解决问题】‎ 如图3，在边长为的等边三角形ABC内有一点P，∠APC=90°，‎ ‎∠BPC=120°，求△APC的面积．‎ ‎ ‎ ‎（4）【拓展应用】‎ 如图4是A，B，C三个村子位置的平面图，经测量AC=4，BC=5，‎ ‎∠ACB=30°，P为△ABC内的一个动点，连接PA，PB，PC．求PA+PB+PC的最小值．‎