绵阳市中考数学试卷及解析 28页

绵阳市2015年中考数学试卷 一、选择题（本大题共12小题，每小题3分，共36分，每小题只有一个选项最符合题目要求）‎ ‎1．（3分）（2015•绵阳）±2是4的（　　）‎ ‎　‎ A．‎ 平方根 B．‎ 相反数 C．‎ 绝对值 D．‎ 算术平方根 ‎2．（3分）（2015•绵阳）下列图案中，轴对称图形是（　　）‎ ‎　‎ A．‎ B．‎ C．‎ D．‎ ‎3．（3分）（2015•绵阳）若+|2a﹣b+1|=0，则（b﹣a）2015=（　　）‎ ‎　‎ A．‎ ‎﹣1‎ B．‎ ‎1‎ C．‎ ‎52015‎ D．‎ ‎﹣52015‎ ‎4．（3分）（2015•绵阳）福布斯2015年全球富豪榜出炉，中国上榜人数仅次于美国，其中王健林以242亿美元的财富雄踞中国内地富豪榜榜首，这一数据用科学记数法可表示为（　　）‎ ‎　‎ A．‎ ‎0.242×1010美元 B．‎ ‎0.242×1011美元 ‎　‎ C．‎ ‎2.42×1010美元 D．‎ ‎2.42×1011美元 ‎5．（3分）（2015•绵阳）如图，在△ABC中，∠B、∠C的平分线BE，CD相交于点F，∠ABC=42°，∠A=60°，则∠BFC=（　　）‎ ‎　‎ A．‎ ‎118°‎ B．‎ ‎119°‎ C．‎ ‎120°‎ D．‎ ‎121°‎ ‎6．（3分）（2015•绵阳）要使代数式有意义，则x的（　　）‎ ‎　‎ A．‎ 最大值是 B．‎ 最小值是 C．‎ 最大值是 D．‎ 最小值是 ‎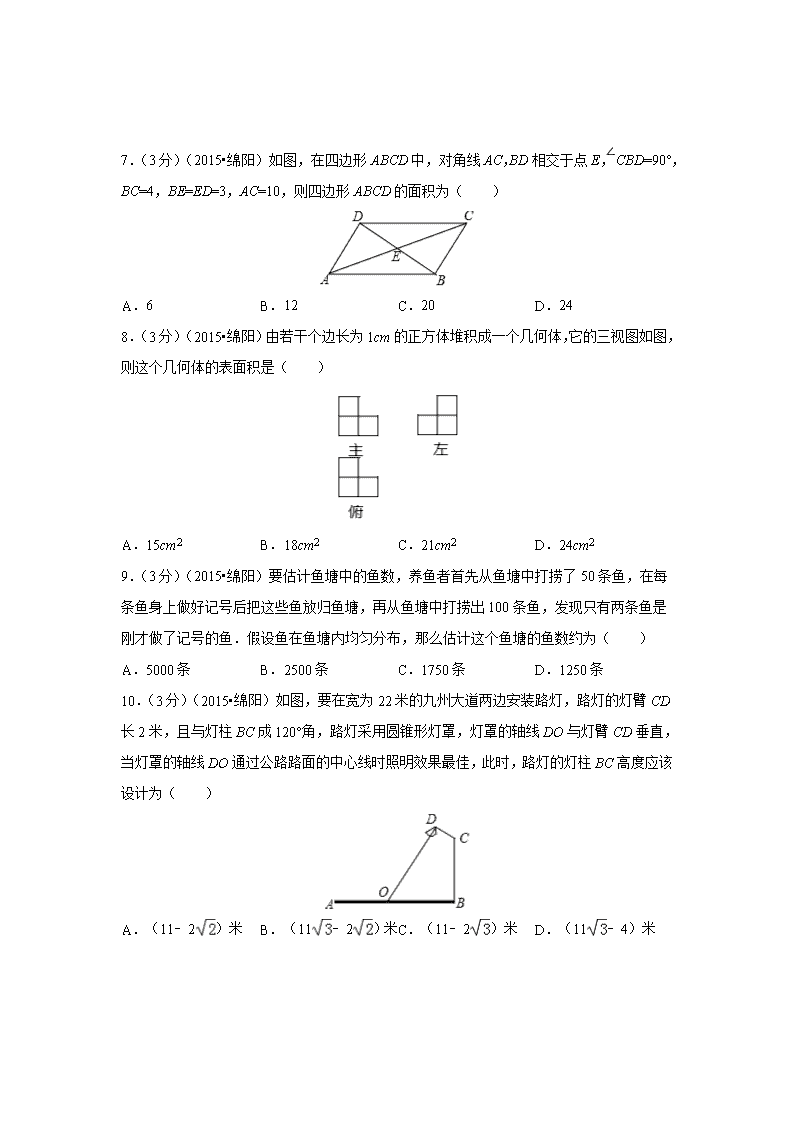7．（3分）（2015•绵阳）如图，在四边形ABCD中，对角线AC，BD相交于点E，∠CBD=90°，BC=4，BE=ED=3，AC=10，则四边形ABCD的面积为（　　）‎ ‎　‎ A．‎ ‎6‎ B．‎ ‎12‎ C．‎ ‎20‎ D．‎ ‎24‎ ‎8．（3分）（2015•绵阳）由若干个边长为1cm的正方体堆积成一个几何体，它的三视图如图，则这个几何体的表面积是（　　）‎ ‎　‎ A．‎ ‎15cm2‎ B．‎ ‎18cm2‎ C．‎ ‎21cm2‎ D．‎ ‎24cm2‎ ‎9．（3分）（2015•绵阳）要估计鱼塘中的鱼数，养鱼者首先从鱼塘中打捞了50条鱼，在每条鱼身上做好记号后把这些鱼放归鱼塘，再从鱼塘中打捞出100条鱼，发现只有两条鱼是刚才做了记号的鱼．假设鱼在鱼塘内均匀分布，那么估计这个鱼塘的鱼数约为（　　）‎ ‎　‎ A．‎ ‎5000条 B．‎ ‎2500条 C．‎ ‎1750条 D．‎ ‎1250条 ‎10．（3分）（2015•绵阳）如图，要在宽为22米的九州大道两边安装路灯，路灯的灯臂CD长2米，且与灯柱BC成120°角，路灯采用圆锥形灯罩，灯罩的轴线DO与灯臂CD垂直，当灯罩的轴线DO通过公路路面的中心线时照明效果最佳，此时，路灯的灯柱BC高度应该设计为（　　）‎ ‎　‎ A．‎ ‎（11﹣2）米 B．‎ ‎（11﹣2）米 C．‎ ‎（11﹣2）米 D．‎ ‎（11﹣4）米 ‎11．（3分）（2015•绵阳）将一些相同的“○”按如图所示的规律依次摆放，观察每个“龟图”中的“○”的个数，若第n个“龟图”中有245个“○”，则n=（　　）‎ ‎　‎ A．‎ ‎14‎ B．‎ ‎15‎ C．‎ ‎16‎ D．‎ ‎17‎ ‎12．（3分）（2015•绵阳）如图，D是等边△ABC边AB上的一点，且AD：DB=1：2，现将△ABC折叠，使点C与D重合，折痕为EF，点E，F分别在AC和BC上，则CE：CF=（　　）‎ ‎　‎ A．‎ B．‎ C．‎ D．‎ 二、填空题（本大题共6小题，每小题3分，共18分）‎ ‎13．（3分）（2015•绵阳）计算：a（a2÷a）﹣a2=　　．‎ ‎14．（3分）（2015•绵阳）如图是轰炸机机群的一个飞行队形，如果最后两架轰炸机的平面坐标分别为A（﹣2，1）和B（﹣2，﹣3），那么第一架轰炸机C的平面坐标是　　．‎ ‎15．（3分）（2015•绵阳）在实数范围内因式分解：x2y﹣3y=　 　．‎ ‎16．（3分）（2015•绵阳）如图，AB∥CD，∠CDE=119°，GF交∠DEB的平分线EF于点F，∠AGF=130°，则∠F=　　．‎ ‎17．（3分）（2015•绵阳）关于m的一元二次方程nm2﹣n2m﹣2=0的一个根为2，则n2+n﹣2=　　．‎ ‎18．（3分）（2015•绵阳）如图，在等边△ABC内有一点D，AD=5，BD=6，CD=4，将△ABD绕A点逆时针旋转，使AB与AC重合，点D旋转至点E，则∠CDE的正切值为　　．‎ 三、解答题（本大题共7小题，共86分，解答时应写出文字说明、证明过程或演算步骤）‎ ‎19．（16分）（2015•绵阳）（1）计算：|1﹣|+（﹣）﹣2﹣+；‎ ‎（2）解方程：=1﹣．‎ ‎　‎ ‎20．（11分）（2015•绵阳）阳泉同学参加周末社会实践活动，到“富乐花乡”蔬菜大棚中收集到20株西红柿秧上小西红柿的个数：‎ ‎32 39 45 55 60 54 60 28 56 41‎ ‎51 36 44 46 40 53 37 47 45 46‎ ‎（1）前10株西红柿秧上小西红柿个数的平均数是　　，中位数是　　，众数是　　；‎ ‎（2）若对这20个数按组距为8进行分组，请补全频数分布表及频数分布直方图 个数分组 ‎28≤x＜36‎ ‎36≤x＜44‎ ‎44≤x＜52‎ ‎52≤x＜60‎ ‎60≤x＜68‎ 频数 ‎2‎ ‎　　‎ ‎　　‎ ‎　　‎ ‎2‎ ‎（3）通过频数分布直方图试分析此大棚中西红柿的长势．‎ ‎　‎ ‎21．（11分）（2015•绵阳）如图，反比例函数y=（k＞0）与正比例函数y=ax相交于A（1，k），B（﹣k，﹣1）两点．‎ ‎（1）求反比例函数和正比例函数的解析式；‎ ‎（2）将正比例函数y=ax的图象平移，得到一次函数y=ax+b的图象，与函数y=（k＞0）的图象交于C（x1，y1），D（x2，y2），且|x1﹣x2|•|y1﹣y2|=5，求b的值．‎ ‎　‎ ‎22．（11分）（2015•绵阳）如图，O是△ABC的内心，BO的延长线和△ABC的外接圆相交于点D，连接DC，DA，OA，OC，四边形OADC为平行四边形．‎ ‎（1）求证：△BOC≌△CDA；‎ ‎（2）若AB=2，求阴影部分的面积．‎ ‎　‎ ‎23．（11分）（2015•绵阳）南海地质勘探队在南沙群岛的一小岛发现很有价值的A，B两种矿石，A矿石大约565吨，B矿石大约500吨，上报公司，要一次性将两种矿石运往冶炼厂，需要不同型号的甲、乙两种货船共30艘，甲货船每艘运费1000元，乙货船每艘运费1200元．‎ ‎（1）设运送这些矿石的总费用为y元，若使用甲货船x艘，请写出y和x之间的函数关系式；‎ ‎（2）如果甲货船最多可装A矿石20吨和B矿石15吨，乙货船最多可装A矿石15吨和B矿石25吨，装矿石时按此要求安排甲、乙两种货船，共有几种安排方案？哪种安排方案运费最低并求出最低运费．‎ ‎　‎ ‎24．（12分）（2015•绵阳）已知抛物线y=﹣x2﹣2x+a（a≠0）与y轴相交于A点，顶点为M，直线y=x﹣a分别与x轴、y轴相交于B，C两点，并且与直线MA相交于N点．‎ ‎（1）若直线BC和抛物线有两个不同交点，求a的取值范围，并用a表示交点M，A的坐标；‎ ‎（2）将△NAC沿着y轴翻转，若点N的对称点P恰好落在抛物线上，AP与抛物线的对称轴相交于点D，连接CD，求a的值及△PCD的面积；‎ ‎（3）在抛物线y=﹣x2﹣2x+a（a＞0）上是否存在点P，使得以P，A，C，N为顶点的四边形是平行四边形？若存在，求出点P的坐标；若不存在，请说明理由．‎ ‎　‎ ‎25．（14分）（2015•绵阳）如图，在边长为2的正方形ABCD中，G是AD延长线时的一点，且DG=AD，动点M从A点出发，以每秒1个单位的速度沿着A→C→G的路线向G点匀速运动（M不与A，G重合），设运动时间为t秒，连接BM并延长AG于N．‎ ‎（1）是否存在点M，使△ABM为等腰三角形？若存在，分析点M的位置；若不存在，请说明理由；‎ ‎（2）当点N在AD边上时，若BN⊥HN，NH交∠CDG的平分线于H，求证：BN=HN；‎ ‎（3）过点M分别作AB，AD的垂线，垂足分别为E，F，矩形AEMF与△ACG重叠部分的面积为S，求S的最大值．‎ 绵阳市2015年中考数学试卷 一、选择题（本大题共12小题，每小题3分，共36分，每小题只有一个选项最符合题目要求）‎ ‎1．（3分）‎ 考点：‎ 平方根．.‎ 分析：‎ 根据平方根的定义解答即可．‎ 解答：‎ 解：±2是4的平方根．‎ 故选：A．‎ 点评：‎ 本题考查了平方根的定义，是基础题，熟记概念是解题的关键．‎ ‎2．（3分）‎ 考点：‎ 轴对称图形．.‎ 分析：‎ 根据轴对称图形的概念对各图形分析判断后即可求解．‎ 解答：‎ 解：A、不是轴对称图形，故此选项错误；‎ B、不是轴对称图形，故此选项错误；‎ C、不是轴对称图形，故此选项错误；‎ D、是轴对称图形，故此选项正确；‎ 故选；D．‎ 点评：‎ 本题考查了轴对称图形，图形两部分沿对称轴折叠后可重合，轴对称图形的关键是寻找对称轴．‎ ‎3．（3分）‎ 考点：‎ 解二元一次方程组；非负数的性质：绝对值；非负数的性质：算术平方根．.‎ 专题：‎ 计算题．‎ 分析：‎ 利用非负数的性质列出方程组，求出方程组的解得到a与b的值，即可确定出原式的值．‎ 解答：‎ 解：∵+|2a﹣b+1|=0，‎ ‎∴，‎ 解得：，‎ 则（b﹣a）2015=（﹣3+2）2015=﹣1．‎ 故选：A．‎ 点评：‎ 此题考查了解二元一次方程组，以及非负数的性质，熟练掌握运算法则是解本题的关键．‎ ‎4．（3分）‎ 考点：‎ 科学记数法—表示较大的数．.‎ 分析：‎ 科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．‎ 解答：‎ 解：将242亿用科学记数法表示为：2.42×1010．‎ 故选：C．‎ 点评：‎ 此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．‎ ‎5．（3分）‎ 考点：‎ 三角形内角和定理．.‎ 分析：‎ 由三角形内角和定理得∠ABC+∠ACB=120°，由角平分线的性质得∠CBE+∠BCD=60°，再利用三角形的内角和定理得结果．‎ 解答：‎ 解：∵∠A=60°，‎ ‎∴∠ABC+∠ACB=120°，‎ ‎∵BE，CD是∠B、∠C的平分线，‎ ‎∴∠CBE=∠ABC，∠BCD=，‎ ‎∴∠CBE+∠BCD=（∠ABC+∠BCA）=60°，‎ ‎∴∠BFC=180°﹣60°=120°，‎ 故选：C．‎ 点评：‎ 本题主要考查了三角形内角和定理和角平分线的性质，综合运用三角形内角和定理和角平分线的性质是解答此题的关键．‎ ‎6．（3分）‎ 考点：‎ 二次根式有意义的条件．.‎ 分析：‎ 根据二次根式有意义的条件列出关于x的不等式，求出x的取值范围即可．‎ 解答：‎ 解：∵代数式有意义，‎ ‎∴2﹣3x≥0，解得x≤．‎ 故选：A．‎ 点评：‎ 本题考查的是二次根式有意义的条件，熟知二次根式具有非负性是解答此题的关键．‎ ‎7．（3分）‎ 考点：‎ 平行四边形的判定与性质；全等三角形的判定与性质；勾股定理．.‎ 分析：‎ 根据勾股定理，可得EC的长，根据平行四边形的判定，可得四边形ABCD的形状，根据平行四边形的面积公式，可得答案．‎ 解答：‎ 解：在Rt△BCE中，由勾股定理，得 CE===5．‎ ‎∵BE=DE=3，AE=CE=5，‎ ‎∴四边形ABCD是平行四边形．‎ 四边形ABCD的面积为BC•BD=4×（3+3）=24，‎ 故选：D．‎ 点评：‎ 本题考查了平行四边形的判定与性质，利用了勾股定理得出CE的长，又利用对角线互相平分的四边形是平行四边形，最后利用了平行四边形的面积公式．‎ ‎8．（3分）‎ 考点：‎ 由三视图判断几何体；几何体的表面积．.‎ 分析：‎ 主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形．‎ 解答：‎ 解：综合三视图，我们可以得出，这个几何模型的底层有2+1=3个小正方体，第二层应该有1个小正方体，‎ 因此搭成这个几何体模型所用的小正方体的个数是3+1=4个．‎ 所以表面积为3×6=18cm2．‎ 故选：B．‎ 点评：‎ 考查学生对三视图掌握程度和灵活运用能力，同时也体现了对空间想象能力方面的考查．如果掌握口诀“俯视图打地基，正视图疯狂盖，左视图拆违章”就更容易得到答案．‎ ‎9．（3分）‎ 考点：‎ 用样本估计总体．.‎ 分析：‎ 首先求出有记号的2条鱼在100条鱼中所占的比例，然后根据用样本中有记号的鱼所占的比例等于鱼塘中有记号的鱼所占的比例，即可求得鱼的总条数．‎ 解答：‎ 解：由题意可得：50÷=2500（条）．‎ 故选：B．‎ 点评：‎ 本题考查了统计中用样本估计总体，表示出带记号的鱼所占比例是解题关键．‎ ‎10．（3分）‎ 考点：‎ 解直角三角形的应用．.‎ 分析：‎ 出现有直角的四边形时，应构造相应的直角三角形，利用相似求得PB、PC，再相减即可求得BC长．‎ 解答：‎ 解：如图，延长OD，BC交于点P．‎ ‎∵∠ODC=∠B=90°，∠P=30°，OB=11米，CD=2米，‎ ‎∴在直角△CPD中，DP=DC•cot30°=2m，PC=CD÷（sin30°）=4米，‎ ‎∵∠P=∠P，∠PDC=∠B=90°，‎ ‎∴△PDC∽△PBO，‎ ‎∴=，‎ ‎∴PB===11米，‎ ‎∴BC=PB﹣PC=（11﹣4）米．‎ 故选：D．‎ 点评：‎ 本题通过构造相似三角形，综合考查了相似三角形的性质，直角三角形的性质，锐角三角函数的概念．‎ ‎11．（3分）‎ 考点：‎ 规律型：图形的变化类．.‎ 分析：‎ 分析数据可得：第1个图形中小圆的个数为5；第2个图形中小圆的个数为7；第3个图形中小圆的个数为11；第4个图形中小圆的个数为17；则知第n个图形中小圆的个数为n（n﹣1）+5．据此可以再求得“龟图”中有245个“○”是n的值．‎ 解答：‎ 解：第一个图形有：5个○，‎ 第二个图形有：2×1+5=7个○，‎ 第三个图形有：3×2+5=11个○，‎ 第四个图形有：4×3+5=17个○，‎ 由此可得第n个图形有：[n（n﹣1）+5]个○，‎ 则可得方程：[n（n﹣1）+5]=245‎ 解得：n1=16，n2=﹣15（舍去）．‎ 故选：C．‎ 点评：‎ 此题主要考查了图形的规律以及数字规律，通过归纳与总结结合图形得出数字之间的规律是解决问题的关键，注意公式必须符合所有的图形．‎ ‎12．（3分）‎ 考点：‎ 翻折变换（折叠问题）．.‎ 分析：‎ 借助翻折变换的性质得到DE=CE；设AB=3k，CE=x，则AE=3k﹣x；根据余弦定理分别求出CE、CF的长即可解决问题．‎ 解答：‎ 解：设AD=k，则DB=2k；‎ ‎∵△ABC为等边三角形，‎ ‎∴AB=AC=3k，∠A=60°；‎ 设CE=x，则AE=3k﹣x；‎ 由题意知：‎ EF⊥CD，且EF平分CD，‎ ‎∴CE=DE=x；‎ 由余弦定理得：‎ DE2=AE2+AD2﹣2AE•AD•cos60°‎ 即x2=（3k﹣x）2+k2﹣2k（3k﹣x）cos60°，‎ 整理得：x=，‎ 同理可求：CF=，‎ ‎∴CE：CF=4：5．‎ 故选：B．‎ 点评：‎ 主要考查了翻折变换的性质及其应用问题；解题的关键是借助余弦定理分别求出CE、CF的长度（用含有k的代数式表示）；对综合的分析问题解决问题的能力提出了较高的要求．‎ 二、填空题（本大题共6小题，每小题3分，共18分）‎ ‎13．（3分）‎ 考点：‎ 整式的混合运算．.‎ 分析：‎ 首先将括号里面利整式的除法运算法则化简，进而利用同底数幂的乘法以及合并同类项法则求出即可．‎ 解答：‎ 解：a（a2÷a）﹣a2=a2﹣a2=0．‎ 故答案为：0．‎ 点评：‎ 此题主要考查了整式的混合运算，正确掌握相关法则是解题关键．‎ ‎14．（3分）‎ 考点：‎ 坐标确定位置．.‎ 分析：‎ 根据A（﹣2，1）和B（﹣2，﹣3）的坐标以及与C的关系进行解答即可．‎ 解答：‎ 解：因为A（﹣2，1）和B（﹣2，﹣3），‎ 所以可得点C的坐标为（2，﹣1），‎ 故答案为：（2，﹣1）．‎ 点评：‎ 此题考查坐标问题，关键是根据A（﹣2，1）和B（﹣2，﹣3）的坐标以及与C的关系解答．‎ ‎15．（3分）‎ 考点：‎ 实数范围内分解因式．.‎ 专题：‎ 计算题．‎ 分析：‎ 原式提取y，再利用平方差公式分解即可．‎ 解答：‎ 解：原式=y（x2﹣3）=y（x﹣）（x+），‎ 故答案为：y（x﹣）（x+）．‎ 点评：‎ 此题考查了实数范围内分解因式，熟练掌握因式分解的方法是解本题的关键．‎ ‎16．（3分）‎ 考点：‎ 平行线的性质．.‎ 分析：‎ 先根据平行线的性质求出∠AED与∠DEB的度数，再由角平分线的性质求出∠DEF的度数，进而可得出∠GEF的度数，再根据三角形外角的性质即可得出结论．‎ 解答：‎ 解：∵AB∥CD，∠CDE=119°，‎ ‎∴∠AED=180°﹣119°=61°，∠DEB=119°．‎ ‎∵GF交∠DEB的平分线EF于点F，‎ ‎∴∠GEF=×119°=59.5°，‎ ‎∴∠GEF=61°+59.5°=120.5°．‎ ‎∵∠AGF=130°，‎ ‎∴∠F=∠AGF﹣∠GEF=130°﹣120.5°=9.5°．‎ 故答案为：9.5°．‎ 点评：‎ 本题考查的是平行线的性质，用到的知识点为：两直线平行，同旁内角互补，内错角相等．‎ ‎17．（3分）．‎ 考点：‎ 一元二次方程的解．.‎ 专题：‎ 计算题．‎ 分析：‎ 先根据一元二次方程的解的定义得到4n﹣2n2﹣2=0，两边除以2n得n+=2，再利用完全平方公式变形得到原式=（n+）2﹣2，然后利用整体代入的方法计算．‎ 解答：‎ 解：把m=2代入nm2﹣n2m﹣2=0得4n﹣2n2﹣2=0，‎ 所以n+=2，‎ 所以原式=（n+）2﹣2‎ ‎=（2）2﹣2‎ ‎=26．‎ 故答案为：26．‎ 点评：‎ 本题考查了一元二次方程的解（根）的意义：能使一元二次方程左右两边相等的未知数的值是一元二次方程的解．又因为只含有一个未知数的方程的解也叫做这个方程的根，所以，一元二次方程的解也称为一元二次方程的根．也考查了代数式的变形能力．‎ ‎18．（3分）‎ 考点：‎ 旋转的性质；等边三角形的性质；解直角三角形．.‎ 专题：‎ 计算题．‎ 分析：‎ 先根据等边三角形的性质得AB=AC，∠BAC=60°，再根据旋转的性质得AD=AE=5，∠DAE=∠BNAC=60°，CE=BD=6，于是可判断△ADE为等边三角形，得到DE=AD=5；过E点作EH⊥CD于H，如图，设DH=x，则CH=4﹣x，利用勾股定理得到52﹣x2=62﹣（4﹣x）2，解得x=，再计算出EH，然后根据正切的定义求解．‎ 解答：‎ 解：∵△ABC为等边三角形，‎ ‎∴AB=AC，∠BAC=60°，‎ ‎∵△ABD绕A点逆时针旋转得△ACE，‎ ‎∴AD=AE=5，∠DAE=∠BNAC=60°，CE=BD=6，‎ ‎∴△ADE为等边三角形，‎ ‎∴DE=AD=5，‎ 过E点作EH⊥CD于H，如图，设DH=x，则CH=4﹣x，‎ 在Rt△DHE中，EH2=52﹣x2，‎ 在Rt△DHE中，EH2=62﹣（4﹣x）2，‎ ‎∴52﹣x2=62﹣（4﹣x）2，解得x=，‎ ‎∴EH==，‎ 在Rt△EDH中，tan∠HDE===3，‎ 即∠CDE的正切值为3．‎ 故答案为：3．‎ 点评：‎ 本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了等边三角形的性质和解直角三角形．‎ ‎　‎ 三、解答题（本大题共7小题，共86分，解答时应写出文字说明、证明过程或演算步骤）‎ ‎19．（16分）‎ 考点：‎ 实数的运算；负整数指数幂；解分式方程；特殊角的三角函数值．.‎ 专题：‎ 计算题．‎ 分析：‎ ‎（1）原式第一项利用绝对值的代数意义化简，第二项利用负整数指数幂法则计算，第三项利用特殊角的三角函数值计算，最后一项利用立方根定义计算即可得到结果；‎ ‎（2）分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．‎ 解答：‎ 解：（1）原式=﹣1+4﹣﹣2=1；‎ ‎（2）去分母得：3=2x+2﹣2，‎ 解得：x=，‎ 经检验x=是分式方程的解．‎ 点评：‎ 此题考查了实数的运算，熟练掌握运算法则是解本题的关键．‎ ‎20．（11分）‎ 考点：‎ 频数（率）分布直方图；频数（率）分布表；加权平均数；中位数；众数．.‎ 分析：‎ ‎（1）根据平均数的计算公式进行计算求出平均数，再根据中位数和众数的定义即可得出答案；‎ ‎（2）根据所给出的数据分别得出各段的频数，从而补全统计图；‎ ‎（3）根据频数分布直方图所给出的数据分别进行分析即可．‎ 解答：‎ 解：（1）前10株西红柿秧上小西红柿个数的平均数是（32+39+45+55+60+54+60+28+56+41）÷10=47；‎ 把这些数据从小到大排列：28、32、39、41、45、54、55、56、60、60，‎ 最中间的数是（45+54）÷2=49.5，‎ 则中位数是49.5；‎ ‎60出现了2次，出现的次数最多，则众数是60；‎ 故答案为：47，49.5，60；‎ ‎（2）根据题意填表如下：‎ 个数分组 ‎28≤x＜36‎ ‎36≤x＜44‎ ‎44≤x＜52‎ ‎52≤x＜60‎ ‎60≤x＜68‎ 频数 ‎2‎ ‎5‎ ‎7‎ ‎4‎ ‎2‎ 补图如下：‎ 故答案为：5，7，4；‎ ‎（3）此大棚的西红柿长势普遍较好，最少都有28个；‎ 西红柿个数最集中的株数在第三组，共7株；‎ 西红柿的个数分布合理，中间多，两端少．‎ 点评：‎ 本题考查读频数分布直方图的能力和利用统计图获取信息的能力；利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题．‎ ‎21．（11分）‎ 考点：‎ 反比例函数与一次函数的交点问题；一次函数图象与几何变换．.‎ 分析：‎ ‎（1）首先根据点A与点B关于原点对称，可以求出k的值，将点A分别代入反比例函数与正比例函数的解析式，即可得解．‎ ‎（2）分别把点（x1，y1）、（x2，y2）代入一次函数y=x+b，再把两式相减，根据|x1﹣x2|•|y1﹣y2|=5得出|x1﹣x2|=|y1﹣y2|=，然后通过联立方程求得x1、x2的值，代入即可求得b的值．‎ 解答：‎ 解：（1）据题意得：点A（1，k）与点B（﹣k，﹣1）关于原点对称，‎ ‎∴k=1，‎ ‎∴A（1，1），B（﹣1，﹣1），‎ ‎∴反比例函数和正比例函数的解析式分别为y=，y=x；‎ ‎（2）∵一次函数y=x+b的图象过点（x1，y1）、（x2，y2），‎ ‎∴，‎ ‎②﹣①得，y2﹣y1=x2﹣x1，‎ ‎∵|x1﹣x2|•|y1﹣y2|=5，‎ ‎∴|x1﹣x2|=|y1﹣y2|=，‎ 由得x2+bx﹣1=0，‎ 解得，x1=，x2=，‎ ‎∴|x1﹣x2|=|﹣|=||=，‎ 解得b=±1．‎ 点评：‎ 本题考查了反比例函数与正比例函数关于原点对称这一知识点，以及用待定系数法求函数解析式以及一次函数图象上点的坐标特点，利用对称性求出点的坐标是解题的关键．‎ ‎22．（11分）‎ 考点：‎ 三角形的内切圆与内心；全等三角形的判定与性质；扇形面积的计算．.‎ 专题：‎ 计算题．‎ 分析：‎ ‎（1）由于O是△ABC的内心，也是△ABC的外心，则可判断△ABC为等边三角形，所以∠AOB=∠BOC=∠AOC=120°，BC=AC，再根据平行四边形的性质得∠ADC=∠AOC=120°，AD=OC，CD=OA=OB，则根据“SAS”证明△BOC≌△CDA；‎ ‎（2）作OH⊥AB于H，如图，根据等腰三角形的性质和三角形内角和定理得到∠BOH=30°，根据垂径定理得到BH=AH=AB=1，再利用含30度的直角三角形三边的关系得到BH=AH=AB=1，OH=BH=，OB=2OH=‎ ‎，然后根据三角形面积公式和扇形面积公式，利用S阴影部分=S扇形AOB﹣S△AOB进行计算即可．‎ 解答：‎ ‎（1）证明：∵O是△ABC的内心，也是△ABC的外心，‎ ‎∴△ABC为等边三角形，‎ ‎∴∠AOB=∠BOC=∠AOC=120°，BC=AC，‎ ‎∵四边形OADC为平行四边形，‎ ‎∴∠ADC=∠AOC=120°，AD=OC，CD=OA，‎ ‎∴AD=OB，‎ 在△BOC和△CDA中 ‎，‎ ‎∴△BOC≌△CDA；‎ ‎（2）作OH⊥AB于H，如图，‎ ‎∵∠AOB=120°，OA=OB，‎ ‎∴∠BOH=（180°﹣120°）=30°，‎ ‎∵OH⊥AB，‎ ‎∴BH=AH=AB=1，‎ OH=BH=，‎ OB=2OH=，‎ ‎∴S阴影部分=S扇形AOB﹣S△AOB ‎=﹣×2×‎ ‎=．‎ 点评：‎ 本题考查了三角形的内切圆与内心：与三角形各边都相切的圆叫三角形的内切圆，三角形的内切圆的圆心叫做三角形的内心，这个三角形叫做圆的外切三角形．三角形的内心就是三角形三个内角角平分线的交点．也考查了等边三角形的判定与性质和扇形面积的计算．‎ ‎23．（11分）‎ 考点：‎ 一次函数的应用；一元一次不等式组的应用．.‎ 分析：‎ ‎（1）根据这些矿石的总费用为y=甲货船运费+乙货船运费，即可解答；‎ ‎（2）根据A矿石大约565吨，B矿石大约500吨，列出不等式组，确定x的取值范围，根据x为整数，确定x的取值，即可解答．‎ 解答：‎ 解：（1）根据题意得：y=1000x+1200（30﹣x）=36000﹣200x．‎ ‎（2）设安排甲货船x艘，则安排乙货船30﹣x艘，‎ 根据题意得：，‎ 化简得：，‎ ‎∴23≤x≤25，‎ ‎∵x为整数，‎ ‎∴x=23，24，25，‎ 方案一：甲货船23艘，则安排乙货船7艘，‎ 运费y=36000﹣200×23=31400元；‎ 方案二：甲货船24艘，则安排乙货船6艘，‎ 运费y=36000﹣200×24=31200元；‎ 方案三：甲货船25艘，则安排乙货船5艘，‎ 运费y=36000﹣200×25=31000元；‎ 经分析得方案三运费最低，为31000元．‎ 点评：‎ 本题考查了一次函数的应用，解决本题的关键是关键题意得到函数解析式和不等式组．‎ ‎24．（12分）‎ 考点：‎ 二次函数综合题．.‎ 分析：‎ ‎（1）先联立抛物线与直线的解析式得出关于x的方程，再由直线BC和抛物线有两个不同交点可知△＞0，求出a的取值范围，令x=0求出y的值即可得出A点坐标，把抛物线的解析式化为顶点式的形式即可得出M点的坐标；‎ ‎（2）利用待定系数法求出直线MA的解析式，联立两直线的解析式可得出N点坐标，进而可得出P点坐标，根据S△PCD=S△PAC﹣S△ADC可得出结论；‎ ‎（3）分点P在y轴左侧与右侧两种情况进行讨论即可．‎ 解答：‎ 解：（1）由题意得，，整理得2x2+5x﹣4a=0．‎ ‎∵△=25+32a＞0，解得a＞﹣．‎ ‎∵a≠0，‎ ‎∴a＞﹣且a≠0．‎ 令x=0，得y=a，‎ ‎∴A（0，a）．‎ 由y=﹣（x+1）2+1+a得，M（﹣1，1+a）．‎ ‎（2）设直线MA的解析式为y=kx+b（k≠0），‎ ‎∵A（0，a），M（﹣1，1+a），‎ ‎∴，解得，‎ ‎∴直线MA的解析式为y=﹣x+a，‎ 联立得，，解得，‎ ‎∴N（，﹣）．‎ ‎∵点P是点N关于y轴的对称点，‎ ‎∴P（﹣，﹣）．‎ 代入y=﹣x2﹣2x+a得，﹣=﹣a2+a+a，解得a=或a=0（舍去）．‎ ‎∴A（0，），C（0，﹣），M（﹣1，），|AC|=，‎ ‎∴S△PCD=S△PAC﹣S△ADC=|AC|•|xp|﹣|AC|•|x0|‎ ‎=••（3﹣1）‎ ‎=；‎ ‎（3）①当点P在y轴左侧时，‎ ‎∵四边形APCN是平行四边形，‎ ‎∴AC与PN互相平分，N（，﹣），‎ ‎∴P（﹣，）；‎ 代入y=﹣x2﹣2x+a得，=﹣a2+a+a，解得a=，‎ ‎∴P（﹣，）．‎ ‎②当点P在y轴右侧时，‎ ‎∵四边形ACPN是平行四边形，‎ ‎∴NP∥AC且NP=AC，‎ ‎∵N（，﹣），A（0，a），C（0，﹣a），‎ ‎∴P（，﹣）．‎ 代入y=﹣x2﹣2x+a得，﹣=﹣a2﹣a+a，解得a=，‎ ‎∴P（，﹣）．‎ 综上所述，当点P（﹣，）和（，﹣）时，A、C、P、N能构成平行四边形．‎ 点评：‎ 本题考查的是二次函数综合题，涉及到二次函数与一次函数的交点问题、二次函数图象上点的坐标特点、平行四边形的判定与性质等知识，难度较大．‎ ‎25．（14分）‎ 考点：‎ 四边形综合题．.‎ 分析：‎ ‎（1）四种情况：当点M为AC的中点时，AM=BM；当点M与点C重合时，AB=BM；当点M在AC上，且AM=2时，AM=AB；当点M为CG的中点时，AM=BM；△ABM为等腰三角形；‎ ‎（2）在AB上截取AK=AN，连接KN；由正方形的性质得出∠ADC=90°，AB=AD，∠CDG=90°，得出BK=DN，先证出∠BKN=∠NDH，再证出∠ABN=∠DNH，由ASA证明△BNK≌△NHD，得出BN=NH即可；‎ ‎（3）①当M在AC上时，即0＜t≤2时，△AMF为等腰直角三角形，得出AF=FM=t，求出S=AF•FM=t2；当t=2时，即可求出S的最大值；‎ ‎②当M在CG上时，即2＜t＜4时，先证明△ACD≌△GCD，得出∠ACD=∠GCD=45°，求出∠ACM=90°，证出△MFG为等腰直角三角形，得出 FG=MG•cos45°=4﹣t，得出S=S△ACG﹣S△CMJ﹣S△FMG，S为t的二次函数，即可求出结果．‎ 解答：‎ ‎（1）解：存在；当点M为AC的中点时，AM=BM，则△ABM为等腰三角形；‎ 当点M与点C重合时，AB=BM，则△ABM为等腰三角形；‎ 当点M在AC上，且AM=2时，AM=AB，则△ABM为等腰三角形；‎ 当点M为CG的中点时，AM=BM，则△ABM为等腰三角形；‎ ‎（2）证明：在AB上截取AK=AN，连接KN；如图1所示：‎ ‎∵四边形ABCD是正方形，‎ ‎∴∠ADC=90°，AB=AD，‎ ‎∴∠CDG=90°，‎ ‎∵BK=AB﹣AK，ND=AD﹣AN，‎ ‎∴BK=DN，‎ ‎∵DH平分∠CDG，‎ ‎∴∠CDH=45°，‎ ‎∴∠NDH=90°+45°=135°，‎ ‎∴∠BKN=180°﹣∠AKN=135°，‎ ‎∴∠BKN=∠NDH，‎ 在Rt△ABN中，∠ABN+∠ANB=90°，‎ 又∵BN⊥NH，‎ 即∠BNH=90°，‎ ‎∴∠ANB+∠DNH=180°﹣∠BNH=90°，‎ ‎∴∠ABN=∠DNH，‎ 在△BNK和△NHD中，‎ ‎，‎ ‎∴△BNK≌△NHD（ASA），‎ ‎∴BN=NH；‎ ‎（3）解：①当M在AC上时，即0＜t≤2时，△AMF为等腰直角三角形，‎ ‎∵AM=t，‎ ‎∴AF=FM=t，‎ ‎∴S=AF•FM=×t×t=t2；‎ 当t=2时，S的最大值=×（2）2=2；‎ ‎②当M在CG上时，即2＜t＜4时，如图2所示：‎ CM=t﹣AC=t﹣2，MG=4﹣t，‎ 在△ACD和△GCD中，‎ ‎，‎ ‎∴△ACD≌△GCD（SAS），‎ ‎∴∠ACD=∠GCD=45°，‎ ‎∴∠ACM=∠ACD+∠GCD=90°，‎ ‎∴∠G=90°﹣∠GCD=45°，‎ ‎∴△MFG为等腰直角三角形，‎ ‎∴FG=MG•cos45°=（4﹣t）•=4﹣t，‎ ‎∴S=S△ACG﹣S△CMJ﹣S△FMG=×4×2﹣×CM×CM﹣×FG×FG ‎=4﹣（t﹣2）2﹣（4﹣）2=﹣+4t﹣8‎ ‎=﹣（t﹣）2+，‎ ‎∴当t=时，S的最大值为．‎ 点评：‎ 本题是相似形综合题目，考查了等腰三角形的判定、正方形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质、三角函数以及三角形面积的计算等知识；本题难度较大，综合性强，特别是（3）中，需要进行分类讨论，通过证明三角形全等和等腰直角三角形才能得出结果．‎