中考数学复习圆专题复习 21页

中考数学专题复习六 几何（圆）‎ ‎【教学笔记】‎ 一、 与圆有关的计算问题（重点）‎ 1、 扇形面积的计算 扇形：扇形面积公式 ‎ ‎：圆心角 ：扇形对应的圆的半径 ：扇形弧长 ：扇形面积 圆锥侧面展开图：‎ ‎（1）=‎ ‎（2）圆锥的体积：‎ 2、 弧长的计算：弧长公式 ； ‎ 3、 角度的计算 二、 圆的基本性质（重点）‎ 1、 切线的性质：圆的切线垂直于经过切点的半径．‎ 2、 圆周角定理：一条弧所对圆周角等于它所对圆心角的一半；‎ 推论：（1）在同圆或等圆中，同弧或等弧所对的圆周角相等；‎ ‎ （2）相等的圆周角所对的弧也相等。‎ ‎ （3）半圆（直径）所对的圆周角是直角。‎ ‎ （4）90°的圆周角所对的弦是直径。‎ 注意：在圆中，同一条弦所对的圆周角有无数个。‎ 3、 垂径定理定理：垂直于弦的直径平分这条弦,并且平分这条弦所对的两段弧 ‎ 推论：（1）平分弦(不是直径)的直径垂直与这条弦,并且平分这条弦所对的两段弧 ‎ （2）弦的垂直平分线经过圆心,并且平分这条弦所对的弧 （3）平分弦所对的一条弧的直径垂直平分这条弦,并且平分这条弦所对的另一条弧 （4）在同圆或者等圆中,两条平行弦所夹的弧相等 三、 圆与函数图象的综合 与圆有关的计算问题 ‎【例1】（2016•资阳）在Rt△ABC中，∠ACB=90°，AC=2，以点B为圆心，BC的长为半径作弧，交AB于点D，若点D为AB的中点，则阴影部分的面积是（　　）‎ A．2﹣π B．4﹣π C．2﹣π D．π ‎【解答】解：∵D为AB的中点，∴BC=BD=AB，∴∠A=30°，∠B=60°．∵AC=2，‎ ‎∴BC=AC•tan30°=2•=2，∴S阴影=S△ABC﹣S扇形CBD=×2×2﹣=2﹣π．‎ 故选A．‎ ‎【例2】（2014•资阳）如图，扇形AOB中，半径OA=2，∠AOB=120°，C是的中点，连接AC、BC，则图中阴影部分面积是（　　）‎ A．﹣2 B． ﹣2 C．﹣ D．﹣‎ 解答：连接OC，‎ ‎∵∠AOB=120°，C为弧AB中点，∴∠AOC=∠BOC=60°，∵OA=OC=OB=2，‎ ‎∴△AOC、△BOC是等边三角形，∴AC=BC=OA=2，‎ ‎∴△AOC的边AC上的高是=，△BOC边BC上的高为，‎ ‎∴阴影部分的面积是﹣×2×+﹣×2×=π﹣2，故选A．‎ ‎【例3】（2013•资阳）钟面上的分针的长为1，从9点到9点30分，分针在钟面上扫过的面积是（　　）‎ ‎　‎ A．‎ π B．‎ π C．‎ π D．‎ π 解答：‎ 从9点到9点30分分针扫过的扇形的圆心角是180°，‎ 则分针在钟面上扫过的面积是：=π．故选：A．‎ ‎【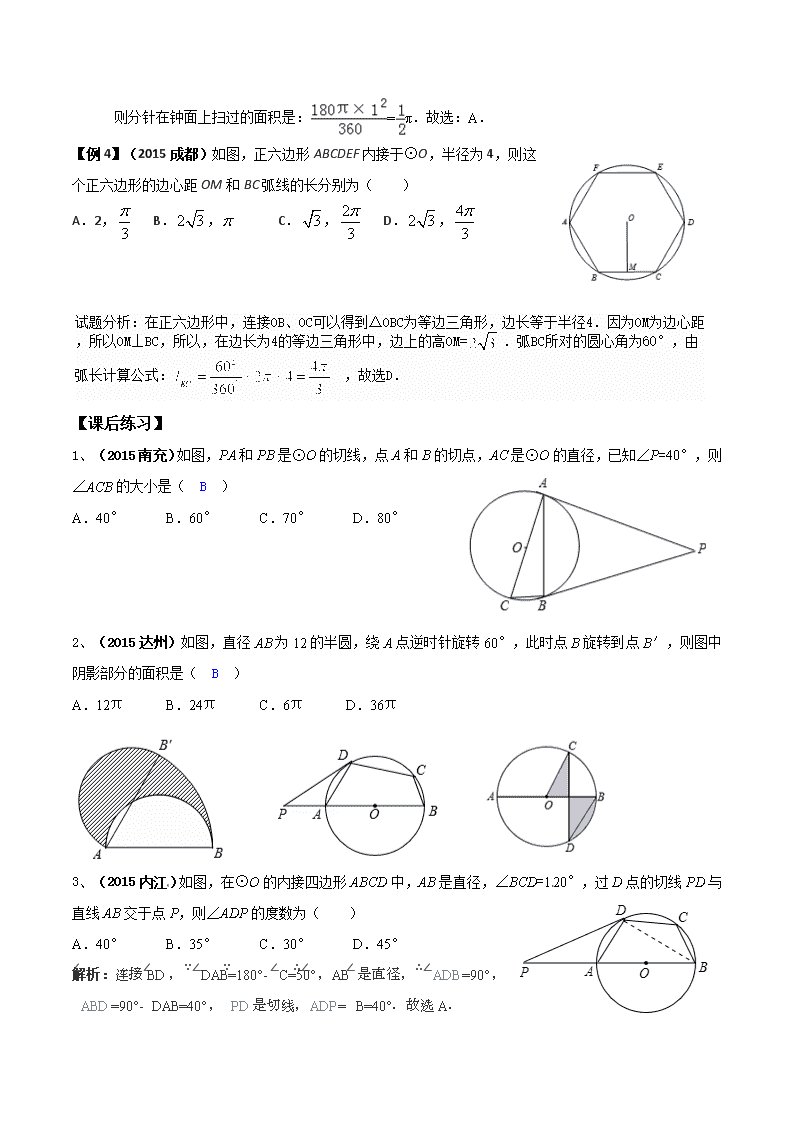例4】（2015成都）如图，正六边形ABCDEF内接于⊙O，半径为4，则这个正六边形的边心距OM和BC弧线的长分别为（ ）‎ A．2， B．，p C．， D．， ‎ ‎【课后练习】‎ 1、 ‎（2015南充）如图，PA和PB是⊙O的切线，点A和B的切点，AC是⊙O的直径，已知∠P=40°，则∠ACB的大小是（　B　）‎ A．40° B．60° C．70° D．80°‎ 2、 ‎（2015达州）如图，直径AB为12的半圆，绕A点逆时针旋转60°，此时点B旋转到点B′，则图中阴影部分的面积是（　B　）‎ A．12π B．24π C．6π D．36π ‎ ‎ 3、 ‎（2015内江）如图，在⊙O的内接四边形ABCD中，AB是直径，∠BCD=120°，过D点的切线PD与直线AB交于点P，则∠ADP的度数为（　　）‎ A．40° B．35° C．30° D．45°‎ 解析：连接BD，∵∠DAB=180°-∠C=50°，AB是直径，∴∠ADB=90°，∠ABD=90°-∠DAB=40°，∵PD是切线，∴∠ADP=∠B=40°．故选A．‎ 1、 ‎（2015自贡）如图，AB是⊙O的直径，弦CD⊥AB，∠CDB＝30°，CD＝，则阴影部分的面积为 A．2π B．π C． D．‎ 解析：∠BOD＝60°‎ ‎ ‎ 2、 ‎（2015凉山州）如图，△ABC内接于⊙O，∠OBC=40°，则∠A的度数为（　　）‎ A．80° B．100° C．110° D．130°‎ 3、 ‎（2015凉山州）将圆心角为90°，面积为4πcm2的扇形围成一个圆锥的侧面，则所围成的圆锥的底面半径 （ ）‎ A．1cm B．2cm C．3cm D．4cm 4、 ‎（2015泸州）如图，PA、PB分别与⊙O相切于A、B两点，若∠C=65°，则∠P的度数为（　　）‎ A．65° B．130° C．50° D．100°‎ 5、 ‎（2015眉山）如图，⊙O是△ABC的外接圆，∠ACO=450，则∠B的度数为（ ）‎ A．300 B．350 C．400 D 450‎ ‎ ‎ 6、 ‎（2015巴中）如图，在⊙O中，弦AC∥半径OB，∠BOC=50°，则∠OAB的度数为（　　）‎ A．25° B．50° C．60° D．30°‎ 7、 ‎（2015攀枝花）如图，已知⊙O的一条直径AB与弦CD相交于点E，且AC=2，AE=，CE=1，则图中阴影部分的面积为（　　）‎ A． B． C． D．‎ 1、 ‎（2015甘孜州）如图，已知扇形AOB的半径为2，圆心角为90°，连接AB，则图中阴影部分的面积是 （ ）‎ A．π﹣2 B．π﹣4 C．4π﹣2 D．4π﹣4‎ 2、 ‎（2015达州）已知正六边形ABCDEF的边心距为cm，则正六边形的半径为 cm．‎ 3、 ‎（2015自贡）如图，已知AB是⊙O的一条直径，延长AB至C点，使AC=3BC，CD与⊙O相切于D点．若CD＝，则劣弧AD的长为 ．‎ ‎ ‎ 4、 ‎（2015遂宁）在半径为5cm的⊙O中，45°的圆心角所对的弧长为 cm．‎ 5、 ‎（2015宜宾）如图，AB为⊙O的直径，延长AB至点D，使BD=OB，DC切⊙O于点C，点B是的中点，弦CF交AB于点E．若⊙O的半径为2，则CF= ．‎ 6、 ‎（2015泸州）用一个圆心角为120°，半径为6的扇形作一个圆锥的侧面，这个圆锥的底面圆的半径是 ．‎ 7、 ‎（2015眉山）已知⊙O的内接正六边形周长为12cm，则这个圆的半经是_________cm．‎ 8、 ‎（2015广安）如图，A．B．C三点在⊙O上，且∠AOB=70°，则∠C= 度．‎ 9、 ‎24．（2015巴中）圆心角为60°，半径为4cm的扇形的弧长为 cm．‎ 10、 ‎（2015甘孜州）如图，AB是⊙O的直径，弦CD垂直平分半径OA，则∠ABC的大小为 度．‎ ‎ ‎ 一、 圆的基本性质 ‎【例1】（2016•资阳）如图，在⊙O中，点C是直径AB延长线上一点，过点C作⊙O的切线，切点为D，连结BD．‎ ‎（1）求证：∠A=∠BDC；‎ ‎（2）若CM平分∠ACD，且分别交AD、BD于点M、N，当DM=1时，求MN的长．‎ ‎【解答】解：（1）如图，连接OD，‎ ‎∵AB为⊙O的直径，∴∠ADB=90°，即∠A+∠ABD=90°，‎ 又∵CD与⊙O相切于点D，∴∠CDB+∠ODB=90°，‎ ‎∵OD=OB，∴∠ABD=∠ODB，∴∠A=∠BDC；‎ ‎（2）∵CM平分∠ACD，∴∠DCM=∠ACM，‎ 又∵∠A=∠BDC，∴∠A+∠ACM=∠BDC+∠DCM，即∠DMN=∠DNM，∵∠ADB=90°，DM=1，∴DN=DM=1，∴MN==．‎ ‎【例2】（2015•资阳）如图11，在△ABC中，BC是以AB为直径的⊙O的切线，且⊙O与AC相交于点D，E为BC的中点，连接DE.‎ ‎（1）求证：DE是⊙O的切线；‎ ‎（2）连接AE，若∠C=45°，求sin∠CAE的值.‎ 解答：解：（1）连接OD，BD，∴OD=OB ∴∠ODB=∠OBD．‎ ‎∵AB是直径，∴∠ADB=90°，∴∠CDB=90°．‎ ‎∵E为BC的中点，∴DE=BE，∴∠EDB=∠EBD，‎ ‎∴∠ODB+∠EDB=∠OBD+∠EBD，即∠EDO=∠EBO．‎ ‎∵BC是以AB为直径的⊙O的切线，∴AB⊥BC，∴∠EBO=90°，∴∠ODE=90°，‎ ‎∴DE是⊙O的切线；‎ （2） 作EF⊥CD于F，设EF=x ‎∵∠C=45°，∴△CEF、△ABC都是等腰直角三角形，∴CF=EF=x，‎ ‎∴BE=CE=x，∴AB=BC=2x，在RT△ABE中，AE==x，‎ ‎∴sin∠CAE==．‎ ‎【例3】（2014•资阳）如图，AB是⊙O的直径，过点A作⊙O的切线并在其上取一点C，连接OC交⊙O于点D，BD的延长线交AC于E，连接AD．‎ ‎（1）求证：△CDE∽△CAD；‎ ‎（2）若AB=2，AC=2，求AE的长．‎ 解答： （1）证明：∵AB是⊙O的直径，∴∠ADB=90°，∴∠B+∠BAD=90°，‎ ‎∵AC为⊙O的切线，∴BA⊥AC，∴∠BAC=90°，即∠BAD+∠DAE=90°，∴∠B=∠CAD，‎ ‎∵OB=OD，∴∠B=∠ODB，而∠ODB=∠CDE，∴∠B=∠CDE，∴∠CAD=∠CDE，‎ 而∠ECD=∠DCA，∴△CDE∽△CAD；‎ ‎（2）解：∵AB=2，∴OA=1，‎ 在Rt△AOC中，AC=2，∴OC==3，∴CD=OC﹣OD=3﹣1=2，‎ ‎∵△CDE∽△CAD，∴=，即=，∴CE=．‎ ‎【例4】（2013•资阳）在⊙O中，AB为直径，点C为圆上一点，将劣弧沿弦AC翻折交AB于点D，连结CD．‎ ‎（1）如图1，若点D与圆心O重合，AC=2，求⊙O的半径r；‎ ‎（2）如图2，若点D与圆心O不重合，∠BAC=25°，请直接写出∠DCA的度数．‎ 解答：‎ ‎（1）如图，过点O作OE⊥AC于E，则AE=AC=‎ ‎×2=1，‎ ‎∵翻折后点D与圆心O重合，∴OE=r，‎ 在Rt△AOE中，AO2=AE2+OE2，即r2=12+（r）2，解得r=；‎ ‎（2）连接BC，∵AB是直径，∴∠ACB=90°，‎ ‎∵∠BAC=25°，∴∠B=90°﹣∠BAC=90°﹣25°=65°，‎ 根据翻折的性质，所对的圆周角等于所对的圆周角，‎ ‎∴∠DCA=∠B﹣∠A=65°﹣25°=40°．‎ ‎【课后练习】‎ 1、 ‎（2015达州）如图，AB为半圆O的在直径，AD、BC分别切⊙O于A、B两点，CD切⊙O于点E，连接OD、OC，下列结论：①∠DOC=90°，②AD+BC=CD，③，④OD：OC=DE：EC，⑤，正确的有（　　）‎ A．2个 B．3个 C．4个 D．5个 解析：如图，连接OE， ∵AD与圆O相切，DC与圆O相切，BC与圆O相切， ∴∠DAO=∠DEO=∠OBC=90°，∴DA=DE，CE=CB，AD∥BC。 ∴CD=DE+EC=AD+BC。结论②正确。 在Rt△ADO和Rt△EDO中，OD=OD，DA=DE，∴Rt△ADO≌Rt△EDO（HL） ∴∠AOD=∠EOD。同理Rt△CEO≌Rt△CBO，∴∠EOC=∠BOC。又∠AOD+∠DOE+∠EOC+∠COB=180°， ∴2（∠DOE+∠EOC）=180°，即∠DOC=90°。结论⑤正确。 ∴∠DOC=∠DEO=90°。又∠EDO=∠ODC，∴△EDO∽△ODC。∴，即OD2=DC•DE。结论①正确。 而，结论④错误。由OD不一定等于OC，结论③错误。∴正确的选项有①②⑤。故选A。‎ 1、 ‎（2015遂宁）如图，在半径为5cm的⊙O中，弦AB=6cm，OC⊥AB于点C，则OC=（　　）‎ A．3cm B．4cm C．5cm D．6cm ‎【解析】连接OA，∵AB=6cm，OC⊥AB于点C，∴AC=AB=×6=3cm，‎ ‎∵⊙O的半径为5cm，∴OC===4cm，‎ 故选B．‎ 2、 ‎（2015广元）如图，已知⊙O的直径AB⊥CD于点E．则下列结论一定错误的是（ ）‎ A．CE=DE B．AE=OE C． D．△OCE≌△ODE 3、 ‎（2015广元）如图，在⊙O中，AB是直径，点D是⊙O上一点，点C是的中点，弦CE⊥AB于点E，过点D的切线交EC的延长线于点G，连接AD，分别交CF、BC于点P、Q，连接AC．给出下列结论：①∠BAD=∠ABC；②GP=GD；③点P是△ACQ的外心．‎ 其中正确结论是_②③④_ （只需填写序号）．‎ 4、 ‎（2015成都）如图，在Rt△ABC中，∠ABC=90°，AC的垂直平分线分别与AC，BC及AB的延长线相交于点D，E，F，且BF=BC．⊙O是△BEF的外接圆，∠EBF的平分线交EF于点G，交于点H，连接BD、FH．（1）求证：△ABC≌△EBF；（2）试判断BD与⊙O的位置关系，并说明理由；‎ ‎（3）若AB=1，求HG•HB的值．‎ 1、 ‎（2015遂宁）如图，AB为⊙O的直径，直线CD切⊙O于点D，AM⊥CD于点M，BN⊥CD于N．（1）求证：∠ADC=∠ABD；（2）求证：AD2=AM•AB；（3）若AM=，sin∠ABD=，求线段BN的长．‎ 解答： （1）证明：连接OD， ∵直线CD切⊙O于点D，∴∠CDO=90°， ‎ ‎∵AB为⊙O的直径，∴∠ADB=90°，∴∠1+∠2=∠2+∠3=90°，∴∠1=∠3，  ∵OB=OD， ∴∠3=∠4，∴∠ADC=∠ABD；  （2）证明：∵AM⊥CD，∴∠AMD=∠ADB=90°，∵∠1=∠4，∴△ADM∽△ABD，  ∴， ∴AD2=AMAB；‎ ‎（3）解：∵sin∠ABD=， ∴sin∠1=， ∵AM=， ∴AD=6， ∴AB=10， ∴BD==8，  ∵BN⊥CD， ∴∠BND=90°， ∴∠DBN+∠BDN=∠1+∠BDN=90°， ∴∠DBN=∠1， ∴sin∠NBD=， ∴DN=， ∴BN==．  ‎ 2、 ‎（2015宜宾）如图，CE是⊙O的直径，BD切⊙O于点D，DE∥BO，CE的延长线交BD于点A．（1）求证：直线BC是⊙O的切线；（2）若AE=2，tan∠DEO=，求AO的长．‎ 1、 ‎（2015泸州）如图，△ABC内接于⊙O，AB=AC，BD为⊙O的弦，且AB∥CD，过点A作⊙O的切线AE与DC的延长线交于点E，AD与BC交于点F．（1）求证：四边形ABCE是平行四边形；（2）若AE=6，CD=5，求OF的长．‎ 解答：（1）证明：∵AE与⊙O相切于点A， ∴∠EAC=∠ABC，  ∵AB=AC，∴∠ABC=∠ACB， ∴∠EAC=∠ACB， ∴AE∥BC，  ∵AB∥CD， ∴四边形ABCE是平行四边形；‎ ‎（2）解：如图，连接AO，交BC于点H，双向延长OF分别交AB，CD与点N，M， ∵AE是⊙O的切线，  由切割线定理得，AE2=EC•DE， ∵AE=6，CD=5，  ∴62=CE（CE+5），解得：CE=4，（已舍去负数），  由圆的对称性，知四边形ABDC是等腰梯形，且AB=AC=BD=CE=4，  又根据对称性和垂径定理，得AO垂直平分BC，MN垂直平分AB，DC，  设OF=x，OH=Y，FH=z， ∵AB=4，BC=6，CD=5， ∴BF=BC﹣FH=3﹣z，DF=CF=BC+FH=3+z，  易得△OFH∽△DMF∽△BFN， ∴，，  即，①  ②， ①+②得：， ①÷②得：，  解得， ∵x2=y2+z2， ∴， ∴x=， ∴OF=．  ‎ 1、 ‎（2015绵阳）如图，O是△ABC的内心，BO的延长线和△ABC的外接圆相交于点D，连接DC，DA，OA，OC，四边形OADC为平行四边形．（1）求证：△BOC≌△CDA；（2）若AB=2，求阴影部分的面积．‎ ‎【解析】 （1）证明：∵O是△ABC的内心，∴∠2=∠3，∠5=∠6，‎ ‎∵∠1=∠2，∴∠1=∠3，由AD∥CO,AD=CO，∴∠4=∠5，∴∠4=∠6，‎ ‎∴△BOC≌△CDA（AAS）‎ 由（1）得，BC=AC,∠3=∠4=∠6，∴∠ABC=∠ACB，∴AB=AC ‎∴△ABC是等边三角形，∴O是△ABC的内心也是外心，∴OA=OB=OC 设E为BD与AC的交点，BE垂直平分AC.在Rt△OCE中，CE=AC=AB=1，∠OCE=30º，‎ ‎∴OA=OB=OC=.∵∠AOC=120º，∴.‎ 2、 ‎（2015广元）如图，AB是⊙O的弦，D为半径OA的中点．过D作CD⊥OA交弦AB于点E，交⊙O于点F．且CE=CB．（1）求证：BC是⊙O的切线；（2）连接AF、BF，求∠ABF的度数；（3）如果CD=15，BE=10，sinA=．求⊙O的半径．‎ 解：（1）证明：连接OB∵OB=OA，CE=CB，∴∠A=∠OBA，∠CEB=∠ABC 又∵CD⊥OA∴∠A+∠AED=∠A+∠CEB=90 °∴∠OBA+∠ABC=90 ° ∴OB⊥BC∴BC是⊙O的切线． （2）连接OF，AF，BF， ∵DA=DO，CD⊥OA，  ∴△OAF是等边三角形， ∴∠AOF=60 °∴∠ABF=∠AOF=30 ° （3）过点C作CG⊥BE于点G，由CE=CB，∴EG=BE=5 又Rt△ADE∽Rt△CGE，∴sin∠ECG=sin∠A=， ∴CE==13 ∴CG==12， ‎ 又CD=15，CE=13， ∴DE=2，  由Rt△ADE∽Rt△CGE得=，∴AD=CG=，∴⊙O的半径为2AD=．‎ 1、 ‎（2015广安）如图，PB为⊙O的切线，B为切点，过B作OP的垂线BA，垂足为C，交⊙O于点A，连接PA、AO，并延长AO交⊙O于点E，与PB的延长线交于点D．（1）求证：PA是⊙O的切线；（2）若，且OC=4，求PA的长和tanD的值．‎ 解：（1）证明：连接OB，则OA=OB，∵OP⊥AB， ∴AC=BC，  ∴OP是AB的垂直平分线， ∴PA=PB，  在△PAO和△PBO中，  ∵PA＝PBPO＝POOA＝OB， ∴△PAO≌△PBO（SSS）  ∴∠PBO=∠PAO，PB=PA，  ∵2+OC2=213， ∴AE=2OA=413，OB=OA=213， 在Rt△APO中，  ∵AC⊥OP， ∴AC2=OC•PC，  解得：PC=9， ∴OP=PC+OC=13，  在Rt△APO中，由勾股定理得：AP=OP2-OA2=313， ∴PB=PA=∵PB为⊙O的切线，B为切点， ∴∠PBO=90°，  ∴∠PAO=90°， 即PA⊥OA， ∴PA是⊙O的切线；  （2）连接BE，∵OCAC=23，且OC=4， ∴AC=6， ∴AB=12，  在Rt△ACO中， 由勾股定理得：AO=AC13， ∵AC=BC，OA=OE，  ∴OC=12BE，OC∥BE， ∴BE=2OC=8，BE∥OP， ∴△DBE∽△DPO， ∴BDPD＝BEOP，  即BD313+BD＝813， 解得：BD=24135， 在Rt△OBD中， tanD=OBBD=21324135=512．‎ 2、 ‎（2015巴中）如图，AB是⊙O的直径，OD⊥弦BC于点F，交⊙O于点E，连结CE、AE、CD，若∠AEC=∠ODC．（1）求证：直线CD为⊙O的切线；（2）若AB=5，BC=4，求线段CD的长．‎ 解：（1）证明：连接OC， ∵∠CEA=∠CBA，∠AEC=∠ODC，∴∠CBA=∠ODC， 又∵∠CFD=∠BFO，∴∠DCB=∠BOF， ∵CO=BO，∴∠OCF=∠B， ∵∠B+∠BOF=90°，∴∠OCF+∠DCB=90°，∴直线CD为⊙O的切线；‎ ‎（2）解：连接AC，∵AB是⊙O的直径，∴∠ACB=90°，∴∠DCO=∠ACB， 又∵∠D=∠B，∴△OCD∽△ACB，‎ ‎ ∵∠ACB=90°，AB=5，BC=4，∴AC=3，∴=，即=，解得；DC=． ‎ 一、 圆与函数图象的综合 ‎【例1】（2015•资阳）如图4，AD、BC是⊙O的两条互相垂直的直径，点P从点O出发，沿O→C→D→O的路线匀速运动，设∠APB=y（单位：度），那么y与点P运动的时间x（单位：秒）的关系图是 （ ）‎ 解答：（1）当点P沿O→C运动时，当点P在点O的位置时，y=90°，当点P在点C的位置时，‎ ‎∵OA=OC，∴y=45°，∴y由90°逐渐减小到45°；‎ ‎（2）当点P沿C→D运动时，根据圆周角定理，可得y≡90°÷2=45°；‎ ‎（3）当点P沿D→O运动时，当点P在点D的位置时，y=45°，当点P在点0的位置时，y=90°，∴y由45°逐渐增加到90°．故选：B．‎ ‎【例2】(2013年四川巴中)如图，在平面直角坐标系中，坐标原点为O，A点坐标为(4,0)，B点坐标为(－1,0)，以AB的中点P为圆心，AB为直径作⊙P交y轴的正半轴于点C.‎ ‎(1)求经过A，B，C三点的抛物线所对应的函数解析式；‎ ‎(2)设M为(1)中抛物线的顶点，求直线MC对应的函数解析式；‎ ‎(3)试说明直线MC与⊙P的位置关系，并证明你的结论．‎ 解：（1）∵A（4，0），B（－1，0）， ∴AB=5，半径是PC=PB=PA= 。∴OP= 。 在△CPO中，由勾股定理得： 。∴C（0，2）。 设经过A、B、C三点抛物线解析式是 ， ‎ 把C（0，2）代入得： ，∴ 。∴ 。 ∴经过A、B、C三点抛物线解析式是 ， （2）∵ ，∴M 。 设直线MC对应函数表达式是y=kx+b， 把C（0，2），M 代入得： ，解得 。 ∴直线MC对应函数表达式是 。 （3）MC与⊙P的位置关系是相切。证明如下：设直线MC交x轴于D， 当y=0时， ，∴ ，OD= 。∴D（ ，0）。 在△COD中，由勾股定理得： ， 又 ， ，∴CD 2 +PC 2 =PD 2 。∴∠PCD=90 0 ，即PC⊥DC。 ∵PC为半径，∴MC与⊙P的位置关系是相切。‎ ‎【课后作业】‎ 一、选择题(每小题3分，共24分)‎ ‎1. 如图，已知A，B，C在⊙O上，下列选项中与∠AOB相等的是（　 　）‎ A． 2∠C B． 4∠B ‎ C． 4∠A D． ∠B＋∠C ‎2.如图，已知AB是△ABC外接圆的直径，∠A＝35°，则∠B的度数是（　 　）‎ A．35° B． 45° ‎ C．55° D．65°‎ ‎3.如图，AB是⊙O的直径，弦CD⊥AB，垂足为M，下列结论不成立的是（ ）‎ A．CM＝DM　　 B．CB＝DB　　‎ C．∠ACD＝∠ADC　 　 D．OM＝MD ‎4．如图，已知⊙O的半径为13，弦AB长为24，则点O到AB的距离是（ ）‎ A． 6 B．5 ‎ C． 4 D．3‎ ‎ ‎ ‎ 第1题图 第2题图 第3题图 第4题图 ‎5. 已知⊙的半径为6，圆心到直线的距离为8，则直线与⊙的位置关系是( )‎ A．相交 B．相切 C．相离 D．无法确定 ‎ ‎6. 圆锥底面圆的半径为3cm，其侧面展开图是半圆，则圆锥母线长为（ ）‎ A．3cm　 B．6cm　　 　‎ C．9cm　 　 　 D．12cm ‎ ‎7．如图，Rt△ABC中，∠ACB＝90°，AC＝4，BC＝6，以斜边AB上的一点O为圆心所作的半圆分别与AC、BC相切于点D、E，则AD的长为（　　）‎ A． 2.5 B． 1.6 ‎ C． 1.5 D． 1‎ ‎8. 如图，直线与x轴、y分别相交与A、B两点，圆心P的坐标为（1，0），圆P与y轴相切与点O.若将圆P沿x轴向左移动，当圆P与该直线相交时，横坐标为整数的点P′的个数是（ ）‎ A．2 B．3 ‎ C．4 D.5‎ ‎ ‎ ‎ 第7题图 第8题图 二、填空题：(每小题3分，共24分)‎ ‎9.如图，为的直径，为的弦，，则的度数为 .‎ ‎10.如图，在△ABC中∠A＝25°，以点C为圆心，BC为半径的圆交AB于点D，交AC于点E，则的度数为 ．‎ ‎11.如图，的一边是⊙O的直径，请你添加一个条件，使是⊙O的切线,你所添加的条件为 .‎ ‎ ‎ 第9题图 第10题图 第11题图 ‎12. 如果圆锥的底面周长是20π，侧面展开后所得的扇形的圆心角为120°，则圆锥的母线长是 ．‎ ‎13.如果一个扇形的弧长等于它的半径，那么此扇形称为“等边扇形”.则半径为2的“等边扇形”的面积为 .‎ ‎14. 如图，AB为⊙O的直径，CD⊥AB，若AB＝10,CD＝8，则圆心O到弦CD的距离为 .‎ ‎15. 如图，⊙A、⊙B、⊙C两两外切，它们的半径都是a，顺次连接三个圆心得到△ABC,则图中阴影部分的面积之和是 .‎ ‎16.如图，直线l与半径为4的⊙O相切于点A，P是⊙O上的一个动点（不与点A重合），过点P作PB⊥，垂足为B，连接PA．设PA＝，PB＝y，则（－y）的最大值是　 　．‎ ‎ ‎ ‎ 第14题图 第15题图 第16题图 三、解答题（本大题共8个小题，满分52分）：‎ ‎17. （本题4分）如图，圆弧形桥拱的跨度米，拱高米，试求拱桥的半径.‎ ‎18．（本题4分）如图，已知AB是⊙O的直径，CD是弦，且CD⊥AB，BC＝6，AC＝8，求sin∠ABD的值.‎ ‎19.（满分6分）如图，已知在以点O为圆心的两个同心圆中，大圆的弦AB交小圆于点C，D ．‎ ‎⑴.求证：AC＝BD；‎ ‎⑵.若大圆的半径R＝10，小圆的半径r＝8，且圆O到直线AB的距离为6，求AC的长．‎ ‎20.（本题6分）如图，以△ABC的一边AB为直径作⊙O，⊙O与BC边的交点恰好为BC的中点D，过点D作⊙O的切线交AC于点E．‎ ‎⑴.求证：DE⊥AC；‎ ‎⑵.若AB＝3DE，求tan∠ACB的值．‎ ‎21. （本题6分） 如图，AB是⊙O的直径，点E是上的一点，‎ ‎∠DBC＝∠BED．‎ ‎⑴.求证：BC是⊙O的切线；‎ ‎⑵.已知AD＝3，CD＝2，求BC的长．‎ ‎22. （本题8分）已知：如图，⊙O的直径AB垂直于弦CD，过点C的切线与直径AB的延长线相交于点P，连结PD．‎ ‎⑴.求证：PD是⊙O的切线．‎ ‎⑵.求证：‎ ‎⑶.若PD＝4，，求直径AB的长．‎ ‎23. （本题8分）已知：AB是⊙O的直径，直线CP切⊙O于点C，过点B作BD⊥CP于D．‎ ‎⑴.求证：△ACB∽△CDB；‎ ‎⑵.若⊙O的半径为1，∠BCP＝30°，求图中阴影部分的面积．‎ ‎24. （本题10分）如图，在平面直角坐标系中，已知A（8,0），B（0，6），圆M经过原点O及点A、B.‎ ‎⑴.求圆M的半径及圆心M的坐标；‎ ‎⑵.过点B作圆M的切线，求直线的解析式；‎ ‎⑶.BOA的平分线交AB于点N，交圆M于点E，求点N的坐标和线段OE的长.‎ ‎ ‎A B E M N O x y ‎【参考答案】‎ ‎1～8: ACDB CBBB； 9. ； 10. ； 11. ； 12. ； 13. ； 14.3；15.； 16.2； 17. 米；18. 。 19. (1).证明过程略；(2). ； 20. (1).证明过程略；(2). ； 21.（1）AB是⊙O的直径，得∠ADB＝90°，从而得出∠BAD＝∠DBC，即∠ABC＝90°，即可证明BC是⊙O的切线；（2）可证明△ABC∽△BDC，则＝，即可得出BC＝； 22.（1）连接OD、OC，证△PDO≌△PCO，求出∠PDO＝90°即可；（2）求出∠A＝∠ADO＝∠PDB，根据相似三角形的判定推出△PDB∽△PAD，得出比例式，即可得出答案；（3）根据相似得出比例式，代入即可求出答案AB=6;23. （1）证明过程略；（2）； 24. ⑴. , ⑵.可证；(3). 。‎