高考文科数学前三道大题训练 6页

‎1、（13分）某市为了了解今年高中毕业生的体能状况，从本市某校高中毕业班中抽取一个班进行铅球测试，成绩在7.95米及以上的为合格。把所得数据进行整理后，分成6组画出频率分布直方图的一部分(如图)，已知从左到右前5个小组的频率分别为0.04，0.10，0.14，0.28，0.30 ，第6小组的频数是7.‎ ‎（1）求这次铅球测试成绩合格的人数；‎ ‎（2）若由直方图来估计这组数据的中位数，指出它在第几组内，并说明理由；‎ ‎（3）若参加此次测试的学生中，有9人的成绩为优秀，现在要从成绩优秀的学生中，随机选出2人参加“毕业运动会”，已知、的成绩均为优秀，求两人至少有1人入选的概率.‎ ‎2.（本小题满分1 2分）‎ ‎ 某高校在2012年的自主招生考试成绩中随机抽取40名学生的笔试成绩，按成绩共分成 五组：第1组，第2组，第3组，第4组，第5组， 得到的频率分布直方图如图所示，同时规定成绩在9()分以上（含90分）的学生为“优秀”， 成绩小于90分的学生为“良好”，且只有成绩为“优秀”的学生才能获得面试资格。‎ ‎(1)求“优秀”和“良好”学生的人数：‎ ‎(2)如果用分层抽样的方法从“优秀”和 ‎ ‎ “良好”的学生中选出10人，求“优 ‎ ‎ 秀”和“良好” 的学生分别选出几人？‎ ‎(3)若甲是在(2)选出的 “优秀”学生中 ‎ ‎ 的一个，则从选出的“优秀”学生中再 ‎ ‎ 选2人参加某专项测试，求甲被选中的 概率是多少？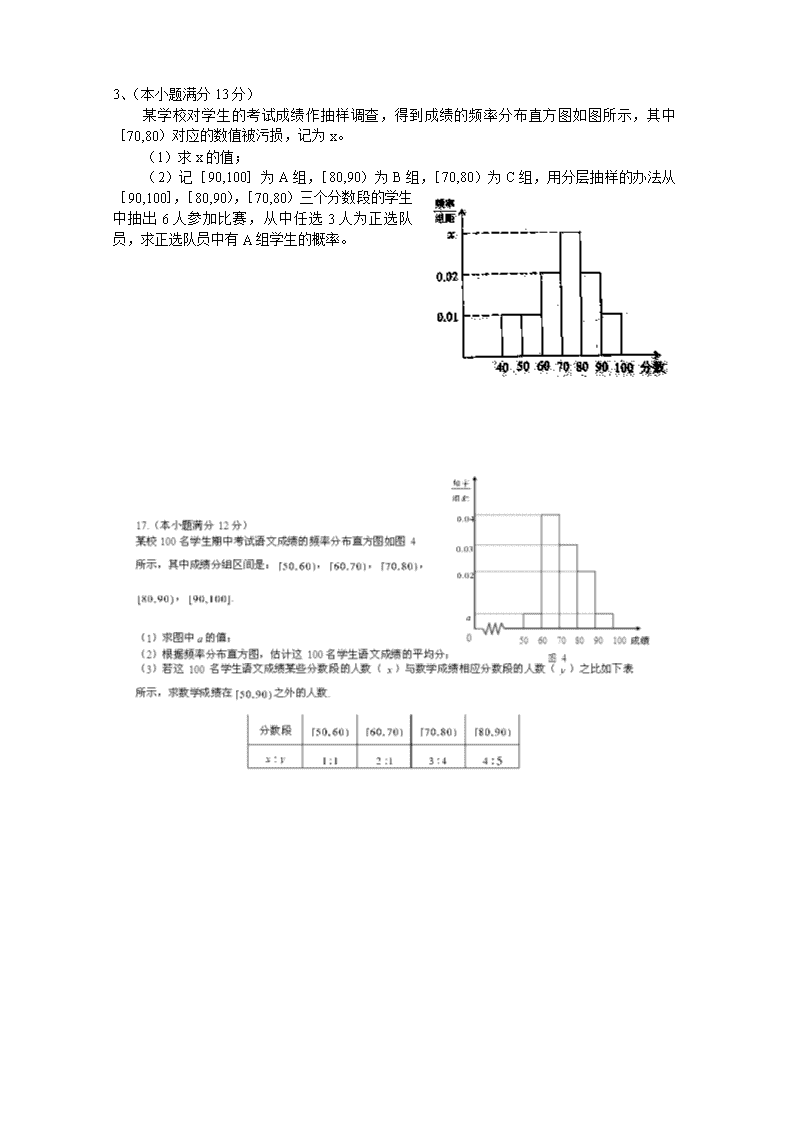‎ ‎3、（本小题满分13分）‎ 某学校对学生的考试成绩作抽样调查，得到成绩的频率分布直方图如图所示，其中［70,80）对应的数值被污损，记为x。‎ ‎（1）求x的值；‎ ‎（2）记［90,100］为A组，［80,90）为B组，［70,80）为C组，用分层抽样的办法从［90,100］，［80,90），［70,80）三个分数段的学生中抽出6人参加比赛，从中任选3人为正选队员，求正选队员中有A组学生的概率。‎ ‎17、（13分）如图，直三棱柱中， ，，，，‎ M、N分别是和的中点．‎ ‎（1）求异面直线与所成的角的余弦； ‎ ‎（2）求三棱锥的体积．‎ ‎18． （本小题满分14分）‎ 如图，矩形中，，．，分别在线段和上，∥，将矩形沿折起．记折起后的矩形为，且平面平面．‎ ‎（Ⅰ）求证：∥平面；‎ ‎（Ⅱ）若，求证：； ‎ ‎（Ⅲ）求四面体体积的最大值． ‎ ‎18．（本小题满分14分）‎ ‎ 在如图所示的多面体ABCDE中，平面ACD，平面ACD,‎ ‎ ，，AD=DE=2，G为AD的中点。‎ ‎ (1)求证：；‎ ‎ (2)在线段CE上找一点F，使得BF//平面ACD并证明；‎ ‎ (3)求三棱锥的体积。‎ ‎18、（本小题满分13分）‎ 如图，矩形ABCD中，对角线AC、BD的交点为G，AD⊥平面ABE，AE⊥EB，AE＝EB＝BC＝2，F为CE上的点，且BF⊥CE。‎ ‎（1）求证：AE⊥平面BCE；‎ ‎（2）求证：AE∥平面BFD；‎ ‎（3）求三棱锥C－GBF的体积。‎ ‎15、（12分）已知向量，，函数 ‎（1）求函数的最小正周期；‎ ‎（2）在中，分别是角的对边，且，，，且，求的值．‎ ‎5. （本小题满分12分）‎ 已知函数 ‎（1）求的最大值和最小正周期；‎ ‎（2）设，，求的值