定积分在高考中的常见题型 4页

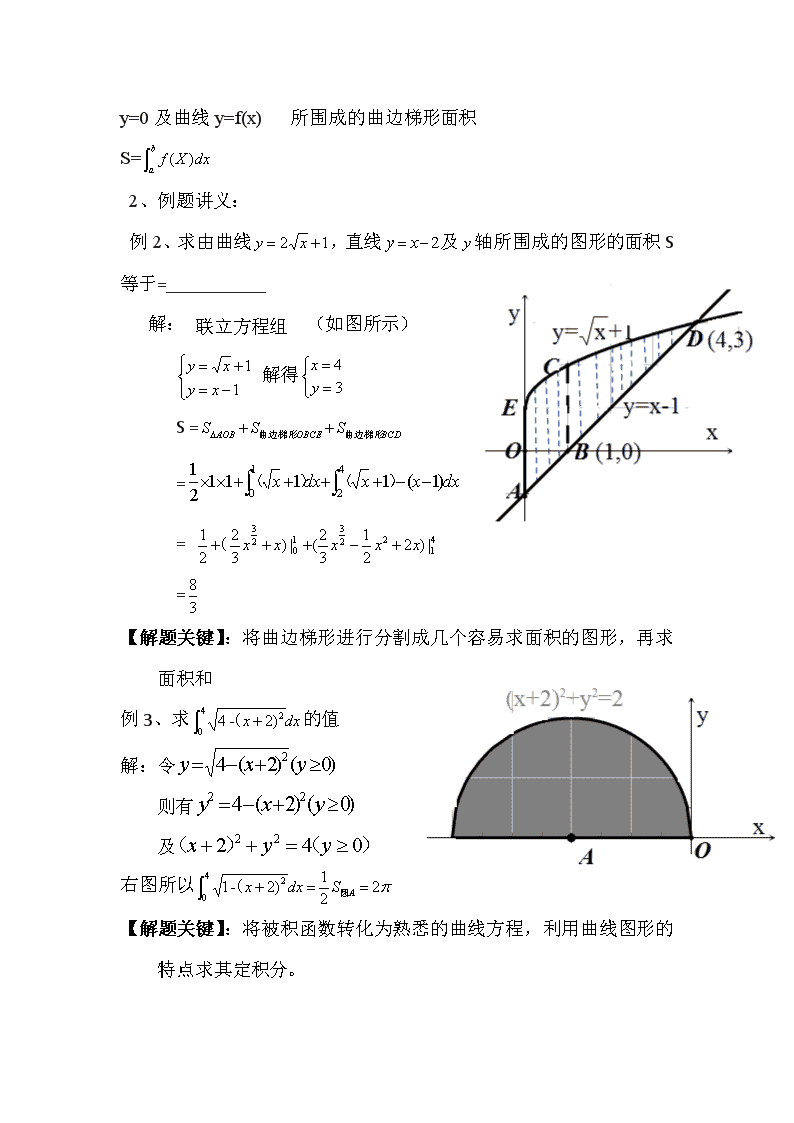
定积分在高考中的常见题型解法 贵州省印江一中（555200） 王代鸿 定积分作为导数的后续课程，与导数运算互为逆运算,也是微积分基本概念之一，同时为大学数学分析打下基础。从高考题中来看，定积分是高考命题的一种新方向，在高考复习中要求学生了解定积分的定义，几何意义，掌握解决问题的方法。‎ 一、利用微积分基本定理求定积分 ‎1、微积分基本定理：一般地，如果是区间上的连续函数，并且，那么.这个结论叫做微积分基本定理（又叫牛顿-莱布尼兹公式）。‎ ‎2、例题讲义 例1、计算 解：因为 ‎ 所以=‎ ‎ 【解题关键】：计算的关键是找到满足的函数。‎ ‎ 跟踪训练：1计算 ‎ 二、利用定积分的几何意义求定积分。‎ ‎ 1、定积分的几何意义 ：设函数y=f(x)在 ‎ 上y=f(x)非负、连续，由直线x=a,x=b, ‎ y=0及曲线y=f(x) 所围成的曲边梯形面积 ‎ S=‎ ‎ 2、例题讲义：‎ ‎ 例2、求由曲线，直线及轴所围成的图形的面积S等于=___________‎ ‎ 解： 联立方程组 （如图所示） ‎ ‎ 解得 ‎ ‎ S = ‎ ‎ =‎ ‎ = ‎ ‎ =‎ ‎【解题关键】：将曲边梯形进行分割成几个容易求面积的图形，再求面积和 例3、求的值 ‎ 解：令 ‎ ‎ 则有 ‎ ‎ 及 右图所以 ‎【解题关键】：将被积函数转化为熟悉的曲线方程，利用曲线图形的特点求其定积分。‎ 练习：由直线，x=2，曲线及x轴所围图形的面积为（ ）‎ ‎ A. B. C. D. ‎ 三、利用变换被积函数求定积分 ‎ 1、从积分变量x分割的几何图形较多，不容易求其定积分时，就变换被积函数求其定积分。‎ ‎ 2、例题讲义 ‎ 例4、求抛物线与直线所围成的图形的面积。‎ 解：方法1分割如右图 如图所示联立方程组 ‎ ‎ 解得 ‎=18‎ 方法2：由得，‎ 由得 ‎ 所以S=‎ ‎【解题关键】：改变被积函数求面积比分割求面积简单 四、定积分与几何概型知识的交叉应用 ‎ 例5、如图，四边形OACB是AB=1,AD=‎ 的矩形，阴影部分是由直线x=1与抛物线围成的区域，在矩形ABCD内（含边界）任意取点，则这点取自阴影部分（含边界）的概率是多少？‎ 解：如图所示本题是古典概型 ‎ ‎ ‎ ‎ ‎ ‎【解题关键】：求曲边梯形OACBD 面积 练习：设区区域，在区域D内任取一点，则此点落在区域内的概率是多少？‎ ‎ ‎ 参考文献 ‎1、《人教版数学选修2-2》‎ ‎2、《新教材完全解读2-2》‎ ‎3、《历年高考试题》‎