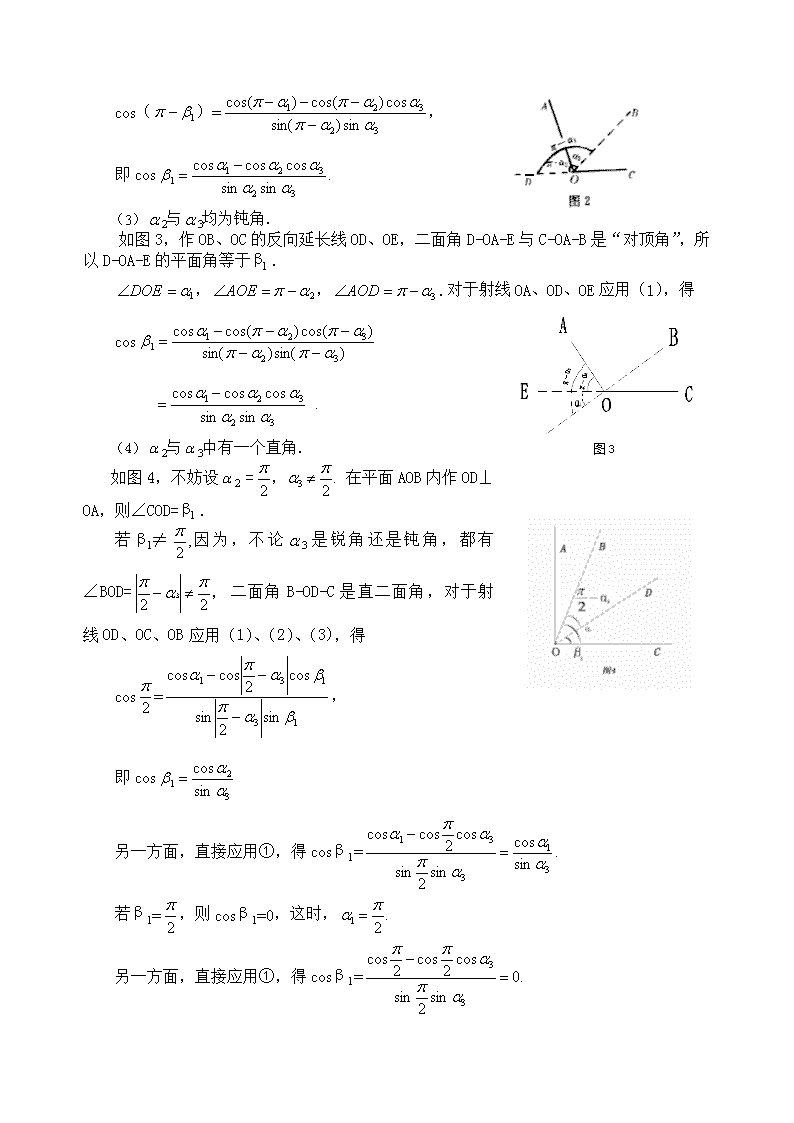三射线定理解高考立体几何题 9页

‎ 三射线定理解高考立体几何题 ‎ 陕西定边县第三中学 白治清 从一点发出的不在同一平面内的三条射线，形成三种空间角（即“线线角”、“面面角”与“线面角” ）。这三种空间角之间的关系问题，是立体几何的一个基本问题，在立体几何的计算、证明中有着十分广泛的应用，本文将探寻这三种空间角之间的关系，得出三射线定理，并用三射线定理解立体几何高考题。‎ 一、由“线线角”求“面面角”‎ 定理1 OA、OB、OC是不在同一平面内的三条射线，如果∠BOC=1 ，∠COA= 2 ‎ ‎， ∠AOB=3 ，二面角C—OA—B，A—OB—C与B—OC—A的平面角分别等于β1 、β2 、β3 ，那么 cosβ1 = 　，　　　① ‎ cosβ2 = 　，　　　②‎ cosβ3 = 　，　　　③‎ 证明：先证明①，分5种情况：‎ （1） ‎ 2与3 ，均为锐角.‎ 如图1，在OA上取一点P，使OP=1.在平面AOB内，作PM⊥OA，交OB于M；在平面AOC内，作PN⊥OA，交OC于N.连结MN，∠NPM=β1 .‎ PN=tan，PM= tan，ON=sec，OM=sec，在△PMN与△OMN中应用余弦定理，得 MN2=tan2+ tan2-2tantan　cosβ1‎ ‎=sec22+ sec2 3-2sec2sec3cos1 .‎ 用1、2、3 的三角函数表示cosβ1 ， 得 ‎ ‎ cosβ1 = ‎ ‎（2）2与3中有一个锐角，一个钝角.‎ 如图2，不妨设3为锐角， 2为钝角，作OC的反向延长线OD.因为二面角D-OA-B与C-OA-B“互补”，所以D-OA-B的平面角等于.‎ ‎∠BOD=对于射线OA、OB、OD应用（1）， 得 cos（）=，‎ 即cos.‎ ‎（3）2与3均为钝角.‎ 如图3， 作OB、OC的反向延长线OD、OE，二面角D-OA-E与C-OA-B是“对顶角”，所以D-OA-E的平面角等于β1 .‎ ‎，，.对于射线OA、OD、OE应用（1），得 cos ‎ .‎ ‎（4）2与3中有一个直角. 图3 ‎ 如图4，不妨设2 = 在平面AOB内作OD⊥OA，则∠COD=β1 .‎ α 若β1≠因为，不论3是锐角还是钝角，都有 ‎∠BOD=二面角B-OD-C是直二面角，对于射线OD、OC、OB应用（1）、（2）、（3)，得 cos=，‎ 即cos 另一方面，直接应用①，得cosβ1=.‎ 若β1=，则cosβ1=0，这时，‎ 另一方面，直接应用①，得cosβ1=‎ 可见，当2、3中有一个直角时，①仍旧适用。‎ ‎（5）2与3均为直角.‎ 这时，β1= 1，cosβ1=cos1 .‎ 另一方面，直接应用①，得cosβ1=‎ 可见，当2、3均为直角时，1①仍旧适用。‎ 综合上述，①得证. 同理可证②与③. 定理1证毕。‎ 二、由“线线角”求“线面角”‎ 定理2 OA、OB、OC是不在同一平面内的三条射线，如果∠BOC=1, ∠COA=2，∠AOB=3，直线OA、OB、OC分别与平面BOC、COA、AOB所成的角等于θ1、θ2、θ3，那么 sin2θ1=(1－cos21－cos22－cos23+2cos1cos2cos3)/sin21. ①‎ sin2θ2=(1－cos21－cos22－cos23+2cos1cos2cos3)/sin22. ②‎ sin2θ3=(1－cos21－cos22－cos23+2cos1cos2cos3)/sin22. ③‎ 证明：先证明①.‎ 在OA上任取一点P，作PQ⊥平面BOC，Q为垂足，OQ是OA在平面BOC内的射影，∠POQ=θ1，分5种情况。‎ ‎（1）OQ在∠BOC的内部.‎ 如图5，作QR⊥OC，垂足为R，连PR，∠PRQ是二面角B-OC-A的平面角，设∠PRQ=.‎ ‎∠OPQ= ∠OPR= ∠QPR=‎ ‎ 二面角O-PR-Q是直二面角，对于射线PR、PO、PQ应用定理1，得 ‎ cos,‎ 即 sinθ1=sin2sinβ3, ‎ sin2θ1=sin22sin2β3, (a)‎ 对于射线OA、OB、OC应用定理1③，得cosβ3=‎ 即sin2β3=1－()2 (b)‎ 将（b）式代入(a)式，得 sin2θ1=‎ ‎ .‎ ‎（2）OQ在∠BOC的两边的反向延长线所形成的角的内部.‎ 如图6 OD、OE是OB、OC的反向延长线，OQ在∠DOE的内部.‎ ‎∠DOE=1，∠AOE=π-2，∠AOD=π-3，对于射线OA、OD、OE应用（1）的结论，得 Sin2=‎ ‎=‎ ‎（3）OQ在∠BOC的一边及另一边的反向延长线所形成的角的内部.‎ 如图7 OD是OC的反向延长线，OQ在∠BOD的内部.‎ ‎∠BOD=∠AOD=对于射线OA、OB、OD应用（1），得 sin21=‎ ‎=‎ ‎（4）OQ在∠BOC的一边上，如图8，OQ在OC上.‎ 这时，1=2，sin21=sin22，另一方面，由定理2①，得 sin21= （c）‎ 因为二面角B-OC-A是直二面角，由定理1③，得 cos 即 （d）‎ 将（d）式代入（c）式，得 sin21=‎ ‎=‎ 可见，当OQ在∠BOC的一边上时，定理2仍旧适用。‎ ‎（5）OQ在∠BOC的一边的反向延长线上；‎ 如图9，OQ在OC的反向延长线OD上.‎ ‎∠BOD=, ∠AOD=‎ 对于射线OA、OB、OD应用（4），得 sin21 = ‎ ‎= .‎ 综合上述，定理2①得证，同理可证②与③，定理2证毕.‎ 三、由“面面角”求“线线角”与“线面角”及由“线面角”求“线线角”与“面面角”.‎ 如果已知“面面角”，那么解定理1的①、②、③联立的方程组，可求得“线线角”，再由定理2可求“线面角”.类似地，由“线面角”可求“线线角”与“面面角”。‎ 应用举例 ‎ ‎ 例1 （2015·陕西·理）如图1，在直角梯形ABCD中，AD∕∕BC,∠BAD=90°,AB=BC=1,AD=2,E是AD的中点，O是AC与BE的交点，将ABE沿BE折起到A1BE的位置，如图2.‎ ‎ （1）证明：CD⊥平面A1OC；‎ ‎ （2）若平面A1BE⊥平面BCDE,求平面A1BC与平面A1CD夹角的余弦值.‎ ‎ ‎ ‎ (图1） （图2）‎ ‎ 服务于本文，只解（2）.其他各题也只解有关三种空间角的问题. ‎ 解：（2）∠BCD = 135°.由(1)得，∠A1CD = 90°.‎ ΔA1OB≌ΔBOC≌ΔCOA1,A1B=A1C=BC,∠A1CB=60°.‎ ‎ 设所求二面角B—A1C—D的平面角为β，对于射线CA1,CB,CD应用三射线定理1，得 ‎ ‎ 平面A1BC与平面A1CD夹角的余弦值为 ‎ ‎ 点评：用三射线定理1求二面角，无需将二面角的平面角作出，只是要先确定三条射线，求出三个线线角.‎ ‎ 例2 （2008·海南·理） 如图，已知点P在正方体ABCD—A1B1C1D1的对角线BD1上，∠PDA=60°.‎ ‎ （1）求DP与CC1所成角的大小；‎ ‎ （2）求DP与平面AA1D1D所成角的大小.‎ ‎ 解：（1)由正方体易知，二面角A—DD1—P的平面角为45°，又∠ADD1=90°，∠PDA=60°.‎ ‎ 对于射线DA,DP,DD1应用三射线定理1，得 ‎ ,‎ ‎ ‎ ‎ ‎ ‎ ∵DD1∥CC1,∴DP与CC1所成的角是45°.‎ ‎ （2）设DP与平面AA1D1D所成的角是θ,对于射线DA，DP,DD1应用三射线定理2，得 ‎ ‎ DP与平面AA1D1D所成的角是30°.‎ 点评：定理1的公式是求二面角的，在二面角已知时，可求线线角；用定理2求线面角时，如果有90°的线线角，实际的运算量很小.‎ 例3 (2006·全国卷1·理）如图， 是互相垂直的两条异面直线，MN是它们的公垂线段、点A，B在 上，点C在 上，AM = MB = MV.‎ ‎ （1）证明：AC⊥NB；‎ ‎ （2) 若∠ACB=60°，求NB与平面ABC所成角的余弦.‎ 解：（2）易知，RtΔBCN ≌ RtΔACN,AC = BC.∠ACB = 60°，∠ABC= 60°‎ 设MB = 1，则 BN = ,BC = 2，∠CBN = 45°.∠ABN = 45°.‎ 设所求的线面角为θ，对于射线BA、BC、BN应用三射线定理2，得 ‎ ‎ ‎ NB与平面ABC所成角的余弦是 ‎ ‎ 点评：定理2的公式虽然很长，但结构特征明鲜，容易记忆.定理的表达式中，有3处余弦平方，有3个余弦值相乘，这看似复杂，但是在具体题目中，线线角的余弦值往往带有根号，这反而使运算变的简便。‎ ‎ 例4 （2014·全国卷1·理）如图，三棱柱ABC—A1B1C1中，侧面BB1C1C为菱形，AB⊥B1C.‎ ‎ (1)证明：AC = AB1；‎ ‎ （2）若AC⊥AB1,∠CBB1=60°，AB=BC,求二面角A—A1B1—C1的余弦值.‎ ‎ 解：（2）二面角B1—AB—C与 ‎ A—A1B1—C1的平面角互补.‎ ‎ 设BC=1,则AB=BB1=B1C=1，AC=AB1= .‎ ‎ 在ΔABB1中，由余弦定理，得 ‎ ‎ ‎ ∵ΔABC ≌ ΔABB1,∴cos∠ABC = cos∠ABB1 = .‎ ‎ sin∠ABC =sin∠ABB1 = .cos∠CBB1 = . ‎ ‎ 设二面角B1—AB—C的平面角为β，对于射线BA，BB1,BC应用三射线定理1，得 ‎ ‎ 二面角 A—A1B1—C的余弦值是 ‎ 点评：借助余弦定理，求出了一个线线角的余弦，为最后应用三射线定理作准备.‎ ‎ 例5 （2000·全国·文）四棱锥P—ABCD的底面是边长为a的正方形，PB⊥平面ABCD.‎ ‎ （1）（略）.‎ ‎ （2）证明无论四棱锥的高怎么变化，面PAD与PCD所成的二面角恒大于 90° ‎ ‎ （2）证明：由已知易得，ΔPAD ≌ RtΔPCD,∠PDA =∠PDC,‎ ‎∠ADC = 90°.‎ 设二面角A—PD—C的平面角为β，对于射线DP,DA,DC应用定理1，得 ‎ ‎ ‎ ∴β＞90°，即面 PAD与PCD所成的二面角恒大于90°.‎ 点评：用三射线定理证明此题，一眼看出，就是“秒杀”.‎ 例6 如图，AB和平面 M所成的角为α，AC在平面M内，AC和AB在平面 M内的射影AB1所成所成的角为β，设∠BAC=θ, 求证：α，β，θ满足关系式：cosθ=cosα·cosβ,‎ ‎ 证明：二面角B—AB1—C是直二面角，由定理1，得 ‎ ‎ ‎ ‎ ‎ ∴cosθ=cosαcosβ 点评：本题结论称为三余弦定理，可看作是三射线定理1的推论.‎ 例7：（2002·全国·理）如图，正方形 ABCD、ABEF的边长都是1，而且平面ABCD、ABEF互相垂直，点M在AC上移动，点N在BF上移动，若cm = BN =(0＜α＜ ） ‎ ‎ （1）求MN的长；‎ ‎ （2）α为何值时，MN的长最小；‎ ‎ （3）当MN的长最小时，求面MNA与面MNB所成二面角的大小.‎ ‎ 解：（3）由（2）得，当M为AC中点，N为BF的中 点时，MN的长最小.‎ ‎ ∠BAC=∠BAN=45°，C— AB—N是直二面角，由三余弦定理，得 ‎ ‎ ‎ ≌‎ ‎ ∠ANB=90°,设所求二面角为β，对于射线NA，NB,NM用三射线定理1，得 ‎ ‎ ‎ ‎ ‎ 点评：借助三余弦定理，求出一个线线角，为最后用三射线定理作准备. ‎ ‎ 例8（2005·全国卷1·理）已知四棱锥P—ABCD的底面是直角梯形，AB∥BC,∠DAB=90°，PA⊥底面ABCD， ‎ ‎ （1）证明：面PAD⊥面PCD；‎ ‎ （2）求AC与PB所成的角；‎ ‎ （3）求面AMC与面BMC所成=面角的大小. B ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ΔMCA≌ΔMCB,∠MCA=∠MCB.∠ABC=90°‎ ‎ 设所求二面角为β，对于射线CM、CA、CB,应用三射线定理1，得 ‎ ‎ ‎ 点评：构建了一个直二面角，这一步是关键.‎ ‎ 例9 （2013·安徽·理）如图，圆锥顶点为 P，底面圆心为O，其母线与底面所成的角为22.5°.AB与CD是底面圆O上的两条平行弦，轴OP与平面PCD所成的角为60°‎ ‎ （1）证明：平面PAB与平面PCD的交线平行于底面；‎ ‎ (2)求cos∠COD. ‎ ‎ 解：（2）作OE⊥CD，连接PE.‎ ‎ 二面角C—OD — P是直二面角，由三余弦定理，得 ‎ （1）‎ ‎ ∠PEO是二面角P—CD—O的平面角，∠PEO=30°，由三射线定理1，得 ‎ (2)‎ ‎ 解（1)和(2)组成的方程组，设cos∠CDP=χ,‎ ‎ cos∠CDO=У,则 ‎ ‎ 点评：本题是历年高考立体几何中的难题，用三射线定理解之，列方程组容易，用常规方法解不易入手.‎ 从理论上讲，在立体几何中，任何一个有关三种空间角的问题，都可以用三射线定理解决.这是因为定理的几何模型十分简单（只有三条射线），使定理具有广泛的适应性；而定理的内含很丰富（揭示了三种空间角之间的关系）。事实上，三射线定理可以全解立体几何（有关三种空间角）高考题。‎ 这里我们已经看到构建几何模型的作用，我们要善于从纷繁的几何图形中，去掉表象成份，抓住核心要件，抽象出简单、基本、能反映问题本质的几何模型。一个模型就是一个题根，也就能解决一个题群.‎ ‎ 最后，请读者朋友用三射线定理解下列各题：‎ ‎ （1）2016年高考全国卷一理科数学（18）题.‎ ‎ （2）2016年高考全国卷二理科数学（19）题.‎ ‎ （3）2016年高考全国卷三理科数学（18）题.‎ 注：本文发表于陕西师范大学《中学数学教学参考》1995年第8期，原标题为《对三种空间角之间关系的探讨》，此次修改在应用部分选用了近年来的高考题.‎ ‎ 2016.9.30‎