江苏高考数学试题和答案含理科附加 12页

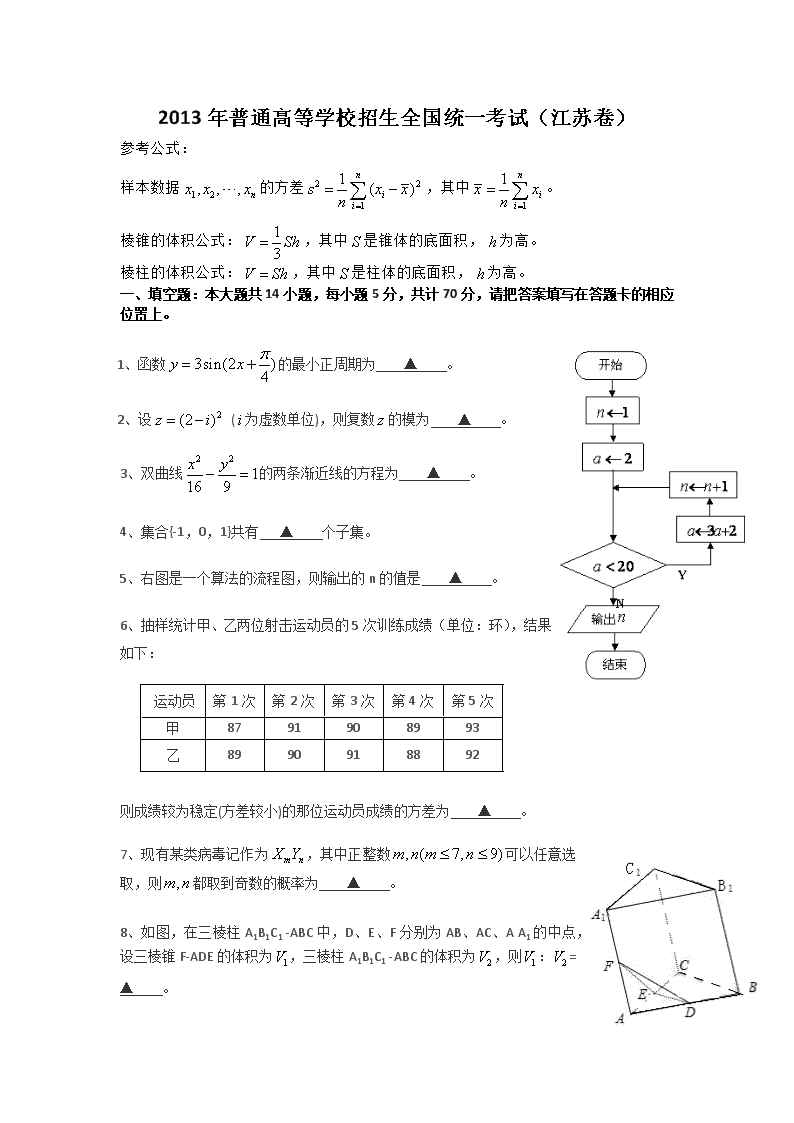
2013 年普通高等学校招生全国统一考试（江苏卷） 参考公式： 样本数据 的方差 ，其中 。 棱锥的体积公式： ，其中 是锥体的底面积， 为高。 棱柱的体积公式： ，其中 是柱体的底面积， 为高。 一、填空题：本大题共 14 小题，每小题 5 分，共计 70 分，请把答案填写在答题卡的相应 位置上。 1、函数 的最小正周期为 ▲ 。 2、设 ( 为虚数单位)，则复数 的模为 ▲ 。 3、双曲线 的两条渐近线的方程为 ▲ 。 4、集合{-1，0，1}共有 ▲ 个子集。 5、右图是一个算法的流程图，则输出的 n 的值是 ▲ 。 6、抽样统计甲、乙两位射击运动员的 5 次训练成绩（单位：环），结果 如下： 则成绩较为稳定(方差较小)的那位运动员成绩的方差为 ▲ 。 7、现有某类病毒记作为 ，其中正整数 可以任意选 取，则 都取到奇数的概率为 ▲ 。 8、如图，在三棱柱 A1B1C1 -ABC 中，D、E、F 分别为 AB、AC、A A1 的中点， 设三棱锥 F-ADE 的体积为 ，三棱柱 A1B1C1 -ABC 的体积为 ，则 ： = ▲ 。 运动员 第 1 次 第 2 次 第 3 次 第 4 次 第 5 次 甲 87 91 90 89 93 乙 89 90 91 88 92 1 2, , , nx x x 2 2 1 1 ( ) n i i s x xn = = −∑ 1 1 n i i x xn = = ∑ 1 3V Sh= S h V Sh= S h 3sin(2 )4y x π= + 2(2 )z i= − i z 2 2 116 9 x y− = m nX Y , ( 7, 9)m n m n≤ ≤ ,m n 1V 2V 1V 2V 9、抛物线 在 处的切线与坐标轴围成三角形区域为 D(包含三角形内部与边界)。 若点 P(x，y)是区域 D 内的任意一点，则 的取值范围是 ▲ 。 10 、 设 D 、 E 分 别 是 △ ABC 的 边 AB 、 BC 上 的 点 ， 且 。 若 ( 、 均为实数)，则 + 的值为 ▲ 。 11、已知 是定义在 R 上的奇函数。当 时， ，则不等式 的解集用区间表示为 ▲ 。 12、在平面直角坐标系 xoy 中，椭圆 C 的方程为 ，右焦点为 F，右准 线为 ，短轴的一个端点为B。设原点到直线BF的距离为 ，F到 的距离为 。若 ， 则椭圆 C 的离心率为 ▲ 。 13、在平面直角坐标系 xoy 中，设定点 A(a,a)，P 是函数 图象上的一动点。若 点 P、A 之间的最短距离为 ，则满足条件的实数 a 的所有值为= ▲ 。 14、在正项等比数列 中， ，则满足 的 最大正整数 n 的值为 ▲ 。 二、解答题：本大题共 6 小题，共计 90 分，请在答题卡指定区域内作答，解答时应写出文字说 明、证明或演算步骤. 15、（本小题满分 14 分） 已知向量 。 （1）若 ，求证： ； （2）设 ，若 ，求 的值。 16、（本小题满分 14 分） 2y x= 1x = 2x y+ 1 2,2 3AD AB BE BC= = 1 2DE AB ACλ λ= +   1 λ 2 λ 1 λ 2 λ ( )f x 0x > 2( ) 4f x x x= − ( )f x x> 2 2 2 2 1( 0)x y a ba b + = > > l 1d l 2d 2 16d d= 1 ( 0)y xx = > 2 2 { }na 5 6 7 1 , 32a a a= + = 1 2 1 2n na a a a a a+ + + >  (cos ,sin ), (cos ,sin ),0a bα α β β β α π= = < < <  | | 2a b− =  a b⊥  (0,1)c = a b c+ =   βα, 如图，在三棱锥 S-ABC 中，平面 平面 SBC, ，AS=AB。过 A 作 ， 垂足为 F，点 E、G 分别为线段 SA、SC 的中点。 求证：（1）平面 EFG//平面 ABC； （2） 。 17、（本小题满分 14 分） 如图，在平面直角坐标系 xoy 中，点 A(0,3)，直线 ，设圆 C 的半径为 1，圆心 在直线 上。 （1）若圆心 C 也在直线 上，过点 A 作圆 C 的切线，求切线的方程； （2）若圆 C 上存在点 M，使 MA=2MO，求圆心 C 的横坐标 的取值范围。 18、（本小题满分 16 分） 如图，游客从某旅游景区的景点 A 处下山至 C 处有两种路径。一种是从 A 沿直线步行到 C， 另一种是先从 A 沿索道乘缆车到 B，然后从 B 沿直线步行到 C。 ⊥SAB BCAB ⊥ SBAF ⊥ BC SA⊥ 42: −= xyl l 1−= xy a 现有甲、乙两位游客从 A 处下山，甲沿 AC 匀速步行，速度为 50 米/分钟。在甲出发 2 分钟后， 乙从 A 乘坐缆车到 B，在 B 处停留 1 分钟后，再从 B 匀速步行到 C。假设缆车速度为 130 米/ 分 钟 ， 山 路 AC 的 长 为 1260 米 ， 经 测 量 ， 。 （1）求索道 AB 的长； （2）问乙出发多少分钟后，乙在缆车上与甲的距离最短？ （3）为使两位游客在 C 处互相等待的时间不超过 3 分钟，乙步 行的速度应控制在什么范围内？ 19、（本小题满分 16 分） 设 是 首 项 为 、 公 差 为 的 等 差 数 列 ， 为 其 前 项 和 。 记 ，其中 c 为实数。 （1）若 c=0，且 成等比数列，证明： （2）若 为等差数列，证明：c=0。 20、（本小题满分 16 分） 设函数 ，其中 为实数。 12 3cos ,cos13 5A C= = }a{ n a d )0( ≠d nS n 2 ,n n nSb n Nn c ∗= ∈+ 421 ,, bbb ),(2 ∗∈= NknSnS knk }b{ n axexgaxxxf x −=−= )(,ln)( a （1）若 在 上是单调减函数，且 在 上有最小值，求 的取值范围； （2）若 在 上是单调增函数，试求 的零点个数，并证明你的结论。 21．[选做题]本题包括 A、B、C、D 四小题，请选定其中两题，并在相应的答题区域内作答．若 多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤． A．[选修 4 - 1：几何证明选讲]（本小题满分 10 分） 如图，AB 和 BC 分别与圆 O 相切于点 D、C，AC 经过圆心 O，且 BC=2OC。 求证：AC=2AD。 B．[选修 4 - 2：矩阵与变换]（本小题满分 10 分） 已知矩阵 ，求矩阵 ． C．[选修 4 - 4：坐标系与参数方程]（本小题满分 10 分） 在平面直角坐标系 中，直线 的参数方程为 （ 为参数），曲线 C 的参数方程为 （ 为参数）。试求直线 和曲线 C 的普通方程，并求出它们的公共点的坐标。 D．[选修 4 - 5：不等式选讲]（本小题满分 10 分） 已知 ≥ ＞0，求证： ≥ 。 【必做题】第 22 题、第 23 题，每题 10 分，共计 20 分．请在答题卡指定区域内作答，解答时应写 出文字说明、证明过程或演算步骤． 22．（本小题满分 10 分） )(xf ),1( +∞ )(xg ),1( +∞ a )(xg ),1( +∞− )(xf 1 0 1 2,0 2 0 6A B −   = =       1A B− xoy l 1 2 x t y t = +  = t 22tan 2tan x y θ θ  =  = θ l a b 3 32a b− 2 22ab a b− 如图，在直三棱柱 中，AB⊥AC，AB=AC=2， =4，点 D 是 BC 的中点。 （1）求异面直线 与 所成角的余弦值； （2）求平面 与平面 所成二面角的正弦值。 23．（本小题满分 10 分） 设数列 ：1，-2，-2，3，3，3，-4，-4，-4，-4，…， ，… 即 当 时 ， 。 记 。 对于 ，定义集合 =﹛ | 为 的整数倍， 且 1≤ ≤ } (1)求 中元素个数； (2)求集合 中元素个数。 参考答案 1．【答案】π 【解析】T＝| 2π ω |＝| 2π 2 |＝π． 2．【答案】5 1 1 1A B C ABC− 1A A 1A B 1C D 1ADC 1ABA { }na 1 1( 1) , ( 1) k k kk k− −− −  个 ( )2 2n k N ∗< ≤ ∈（k- 1）k （k+1）k 1( 1)k na k−= − 1 2n nS a a a= + + + ( )n N ∗∈ l N ∗∈ lP n nS na ,n N ∗∈ n l 11P 2000P 【解析】z＝3－4i，i2＝－1，| z |＝ ＝5． 3．【答案】 【解析】令： ，得 ． 4．【答案】8 【解析】23＝8． 5．【答案】3 【解析】n＝1，a＝2，a＝4，n＝2；a＝10，n＝3；a＝28，n＝4． 6．【答案】2 【解析】易得乙较为稳定，乙的平均值为： ． 方差为： ． 7． 【答案】 【解析】m 取到奇数的有 1，3，5，7 共 4 种情况；n 取到奇数的有 1，3，5，7，9 共 5 种 情况，则 都取到奇数的概率为 ． 8． 【答案】1：24 【解析】三棱锥 与三棱锥 的相似比为 1：2，故体积之比为 1：8．又因 三棱锥 与三棱柱 的体积之比为 1：3．所以，三棱锥 与 三棱柱 的体积之比为 1：24． 9． 【答案】[—2， 1 2] 【解析】抛物线 在 处的切线易得为 y＝2x—1，令 z＝ ，y＝— 1 2x＋ 푧 2． 画出可行域如下，易得过点(0，—1)时，zmin＝—2，过点( 1 2，0)时，zmax＝ 1 2． 10． 【答案】 1 2 xy 4 3±= 0916 22 =− yx xxy 4 3 16 9 2 ±=±= 905 9288919089 =++++=x 25 )9092()9088()9091()9090()9089( 22222 2 =−+−+−+−+−=S 63 20 nm， 63 20 97 54 =× × ADEF − ABCA −1 ABCA −1 ABCCBA −111 ADEF − ABCCBA −111 2xy = 1=x yx 2+ 【解析】 所以， ， ， 1 2． 11． 【答案】(﹣5，0) ∪(5，﹢∞) 【解析】做出 ( )的图像，如下图所示。由于 是定义在 上的奇 函数，利用奇函数图像关于原点对称做出 x＜0 的图像。不等式 ，表示函数 y＝ 的图像在 y＝x 的上方，观察图像易得：解集为(﹣5，0) ∪(5，﹢∞)。 12． 【答案】 【解析】如图，l：x＝ ， ＝ －c＝ ，由等面积得： ＝ 。若 ， 则 ＝ ， 整 理 得 ： ， 两 边 同 除 以 ： ， 得 ： ， 解 之 得 ： ＝ ， 所 以 ， 离 心 率 为 ： ． 13． 【答案】1 或 【解析】 14． 【答案】12 【解析】设正项等比数列 首项为 a1，公比为 q，则： ，得：a1＝ 1 32， q ＝ 2 ， an ＝ 26 － n ． 记 ， )(3 2 2 1 3 2 2 1 ACBAABBCABBEDBDE ++=+=+= ACABACAB 213 2 6 1 λλ +=+−= 6 1 1 −=λ 3 2 2 =λ =+ 21 λλ xxxf 4)( 2 −= 0>x )(xf R xxf >)( )(xf 3 3 c a 2 2d c a 2 c b2 1d a bc 12 6dd = c b2 6 a bc 066 22 =−− baba 2a 066 2 =+    −     a b a b a b 3 6 3 31e 2 =    −= a b 10 }{ na    =+ = 3)1( 2 1 51 41 qqa qa 521 2 12 −=+++= n nn aaaT  ． ，则 ，化简得： ， 当 时， ．当 n＝12 时， ，当 n＝13 时， ，故 nmax＝12． 二、解答题：本大题共 6 小题，共计 90 分．请在答题卡指定区域内作答，解答时应写出文 字说明、证明过程或演算步骤． 15． 解：（1）a－b＝(cosα－cosβ，sinα－sinβ)， |a－b|2＝(cosα－cosβ)2＋(sinα－sinβ)2＝2－2(cosα·cosβ＋sinα·sinβ)＝2， 所以，cosα·cosβ＋sinα·sinβ＝0， 所以， ． （2） ，①2＋②2 得：cos(α－β)＝－ 1 2． 所以，α－β＝ ，α＝ ＋β， 带入②得：sin( ＋β)＋sinβ＝ cosβ＋ 1 2sinβ＝sin( ＋β)＝1， 所以， ＋β＝ ． 所以，α＝ ，β＝ ． 16． 证：（1）因为 SA＝AB 且 AF⊥SB， 所以 F 为 SB 的中点． 又 E，G 分别为 SA，SC 的中点， 所以，EF∥AB，EG∥AC． 又 AB∩AC＝A，AB 面 SBC，AC 面 ABC， 所以，平面 平面 ． （2）因为平面 SAB⊥平面 SBC，平面 SAB∩平面 SBC＝BC， AF 平面 ASB，AF⊥SB． 所以，AF⊥平面 SBC． 又 BC 平面 SBC， 所以，AF⊥BC． 又 AB⊥BC，AF∩AB＝A， 所以，BC⊥平面 SAB． 又 SA 平面 SAB， 2 )1( 21 2 nn nn aaa − ==∏  nnT ∏> 2 )1( 5 22 12 nnn − >− 5 2 11 2 1 2 212 +−>− nnn 52 11 2 1 2 +−> nnn 122 12113 ≈+=n 1212 ∏>T 1313 ∏−=−=′ xx axaxxf a )(xf ′ )(xf ′ a a a 01)( >−=′ axxf )0( ∞+， axxxf −= ln)( )0( ∞+， a a