13平面解析几何含高考题 10页

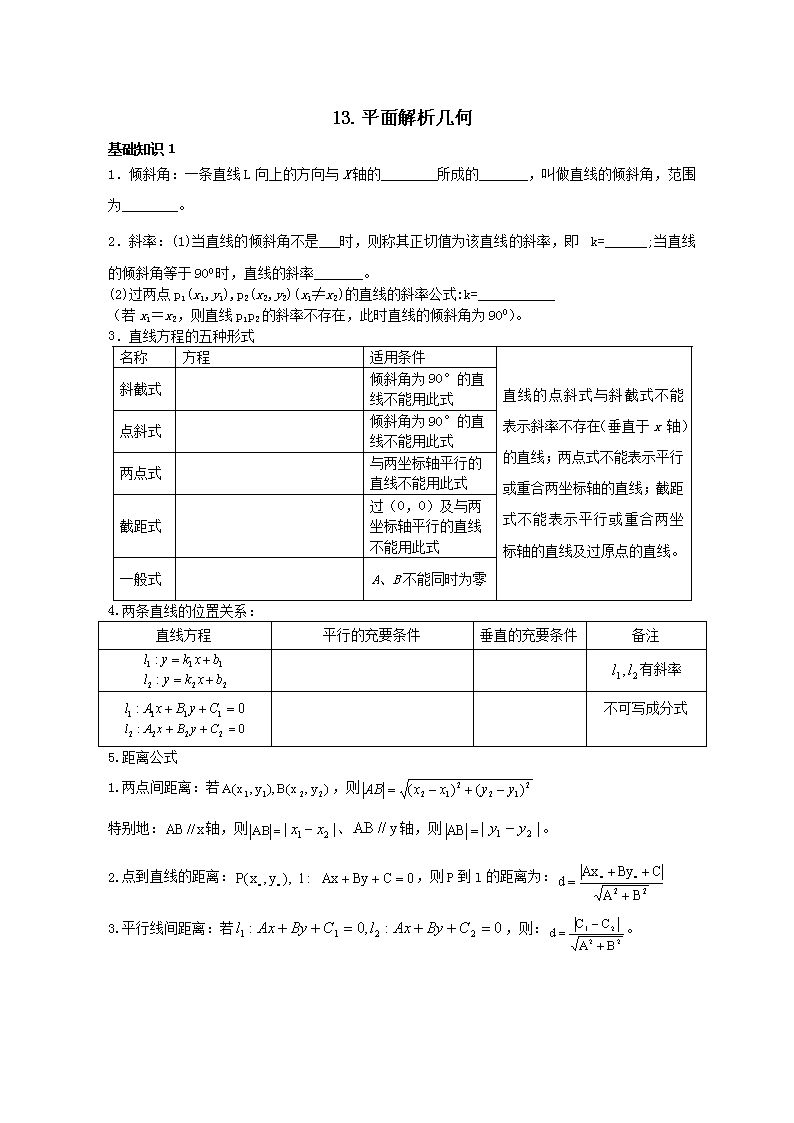
‎13.平面解析几何 基础知识1‎ ‎1．倾斜角：一条直线L向上的方向与X轴的________所成的_______，叫做直线的倾斜角，范围为________。‎ ‎2．斜率：(1)当直线的倾斜角不是___时，则称其正切值为该直线的斜率，即k=______;当直线的倾斜角等于900时，直线的斜率_______。‎ ‎(2)过两点p1(x1,y1),p2(x2,y2)(x1≠x2)的直线的斜率公式:k=___________‎ ‎（若x1＝x2，则直线p1p2的斜率不存在，此时直线的倾斜角为900）。‎ ‎3．直线方程的五种形式 名称 方程 适用条件 直线的点斜式与斜截式不能表示斜率不存在（垂直于x 轴）的直线；两点式不能表示平行或重合两坐标轴的直线；截距式不能表示平行或重合两坐标轴的直线及过原点的直线。‎ 斜截式 倾斜角为90°的直线不能用此式 点斜式 倾斜角为90°的直线不能用此式 两点式 与两坐标轴平行的直线不能用此式 截距式 过（0，0）及与两坐标轴平行的直线不能用此式 一般式 A、B不能同时为零 ‎4.两条直线的位置关系：‎ 直线方程 平行的充要条件 垂直的充要条件 备注 有斜率 不可写成分式 ‎5.距离公式 ‎1.两点间距离：若，则 特别地：轴，则、轴，则。‎ ‎2.点到直线的距离：，则P到l的距离为：‎ ‎3.平行线间距离：若，则：。‎ 巩固训练1‎ ‎1.直线的倾斜角为,斜率为，直线过点,，斜率为，则 ( ) ‎ A B C D 不能确定 ‎2.过点且与直线平行的直线的方程是( )‎ A． B． C． D．‎ ‎3. 已知是第二象限角，直线不经过 ( )‎ A.第一象限 B.第二象限 C.第三象限 D.第四象限 ‎4．直线过点 (－3,－2)且在两坐标轴上的截距相等，则这直线方程为 ( )‎ A. B. ‎ C. 或 D. 或x－y＋5＝0‎ ‎6. 直线与直线平行，则的值为（ ）‎ A.2 B.‎-3 C.2或-3 D.-2或-3‎ ‎7.若直线与垂直，则等于 A.5 B.‎-3 ‎‎ C.5或-3 D不存在 ‎8.已知点，则直线的倾斜角是_________‎ ‎9.直线经过点，且与两坐标轴围成一个等腰直角三角形，直线的方程_________‎ ‎10.已知直线过点，且与轴、轴的正半轴分别交于、两点，为坐标原点，则△OAB面积的最小值为 .‎ ‎11. 已知关于直线的对称点为，则直线的方程是__________________‎ ‎12. 已知点，在直线上求一点P，使最小.‎ ‎13.与直线平行，且距离等于的直线方程是 .‎ ‎14.已知直线与圆相切，则的值为 .‎ ‎15．若直线mx+y+2=0与线段AB有交点，其中A(-2, 3)，B(3,2)，则实数m的取值范围是 ‎　_____________．　‎ 基础知识2‎ ‎1．圆的方程 ‎（1）圆的标准方程：_______________________。圆心为_________，半径为________‎ ‎（2）圆的一般方程________________________，圆心为点_______，半径_________________。‎ 注：二元二次方程，表示圆的方程的充要条件是：‎ ‎ _________________________。‎ 注：求圆的方程常用的方法：待定系数法（标准方程或一般方程）；数形结合求圆心、半径 ‎2．直线与圆的位置关系有三种（）：（1）若；（2）；（3）。‎ 直线与圆相交的弦长__________________.‎ ‎3．两圆位置关系的判定方法：设两圆圆心分别为O1，O2，半径分别为r1，r2，。‎ ‎； ； ；‎ ‎； ；‎ ‎4．点和圆的位置关系的判别转化为点到圆心的距离与半径的大小关系。‎ 点,圆的方程：‎ 如果 _____点在圆外；‎ 如果______点在圆内；‎ 如果______点在圆上。‎ 巩固训练2‎ ‎1.圆的圆心坐标和半径分别为 A. , 6 B. , ‎6 ‎‎ C. , 36 D , 36‎ ‎2斜率为1，与圆相切的直线的方程为 ( )‎ A. B. ‎ C.或 D. 或 ‎3.过圆上一点作圆的切线，则切线方程为 A. B. C. D. ‎ ‎4..圆和圆的位置关系是 （ ）‎ 相离 相交 外切 内切 ‎ ‎5．直线被圆截得的弦长为 （ ）‎ A. B‎.2‎ C.3 D.4‎ ‎6.已知点在圆外，则 A. B. C. 或 D.不能确定 ‎7.方程表示一个圆,则的取值范围是 A B C D ‎ ‎8.过三点, , 的圆的方程为 A. B. ‎ C. D. ‎ ‎9.过坐标原点且与圆相切的直线的方程为_________________‎ ‎10.直线截圆得的劣弧所对的圆心角为_______________‎ ‎11.设直线与圆相交于、两点，且弦的长为，则 .‎ ‎12.直线与圆没有公共点，则的取值范围是__________‎ ‎13.若直线与圆有两个不同的交点，则的取值范围是 .‎ ‎14.圆和圆的位置关系是______________________‎ ‎15.圆上的点到直线的最大距离与最小距离的差是___________‎ 基础知识3‎ ‎1.椭圆与双曲线的性质：‎ 椭 圆 双 曲 线 定义 方程 图形 焦点 焦距 范围 对称轴 顶点 轴 离心率 渐进线 a,b,c ‎2．抛物线的性质 ‎ 标准方程 图形 焦点坐标 准线方程 范围 对称性 顶点 离心率 直线与圆锥曲线相交的弦长公式：__________________________________‎ 巩固训练3‎ ‎1.椭圆的离心率为 ‎ ‎ 2 4‎ ‎2.若抛物线的焦点与椭圆的右焦点重合，则的值为 ‎ ‎ ‎ ‎3. 抛物线的准线方程是 ‎ ‎ ‎4.已知双曲线，则其渐近线方程为 A B C D ‎ ‎5. 曲线与曲线的关系是 A 焦距相等 B 离心率相等 C焦点相同 D有相等的长、短轴 ‎6.抛物线y=4上的一点M到焦点的距离为1，则点M的纵坐标是 ‎ A B C D 0‎ ‎7.已知△ABC的顶点B、C在椭圆＋y2＝1上，顶点A是椭圆的一个焦点，且椭圆的另外一个焦点在BC边上，则△ABC的周长是 A 2 B ‎6 C 4 D 12‎ ‎8.双曲线的虚轴长是实轴长的2倍，则 A B C D ‎ ‎9．过抛物线 y2 = 4x 的焦点作直线交抛物线于A（x1, y1）B（x2, y2）两点，如果=6，那么＝ ‎ ‎ 6 ‎8 ‎ 9 10‎ ‎10.已知是椭圆的两个交点,过且与椭圆长轴垂直的直线交椭圆于A、B两点,若 是正三角形,则此椭圆的离心率是 ‎ ‎ ‎11.已知椭圆中心在原点，一个焦点为F（－2，0），且长轴长是短轴长的2倍，则该椭圆的标准方程是 。‎ ‎12. 若方程表示的图形是双曲线，则的取值范围为 ．。‎ ‎13.顶点在原点,准线方程为的抛物线方程是 。‎ ‎14.已知为椭圆的两个焦点，过的直线交椭圆于A、B两点若，则=______________。‎ ‎15.双曲线的离心率等于，且与椭圆有公共焦点，则该双曲线的方程______‎ ‎16.若该抛物线上的点到焦点的距离是4，则点的坐标为_____‎ ‎17．已知椭圆的长轴长是2，焦点坐标分别是（，0），（，0）.‎ ‎（1）求这个椭圆的标准方程；‎ ‎（2）如果直线与这个椭圆交于两不同的点，求m的取值范围.‎ ‎18.已知椭圆的离心率为，直线与圆相切．（1）求椭圆的方程；（2）设直线与椭圆的交点为，求弦长．‎ ‎19.若点在椭圆上，、分别是椭圆的两焦点，且，求的面积 ‎20.设椭圆的左、右焦点分别、，点 是椭圆短轴的一个端点，且焦距为6，的周长为16．（I）求椭圆的方程；Ⅱ）求过点且斜率为的直线被椭圆所截的线段的中点坐标．‎ ‎09-14年福建高考平面解析几何汇编 ‎（09年）4. 若双曲线的离心率为2，则等于 A. 2 B. C. D. 1‎ ‎22．已知直线经过椭圆的左顶点A和上顶点D，椭圆的右顶点为，点和椭圆上位于轴上方的动点，直线，与直线分别交于两点。（Ⅰ）求椭圆的方程；（Ⅱ）求线段MN的长度的最小值；‎ ‎（10年）11.若点O和点F分别为椭圆的中心和左焦点，点P为椭圆上的任意一点，则的最大值为 ‎ A.2 B.3 C.6 D.8‎ ‎13. 若双曲线-=1(b>0)的渐近线方程式为y=，则ｂ等于　　　　　　　　。‎ ‎19.已知抛物线C：过点A （1 , -2）。‎ ‎（I）求抛物线C 的方程，并求其准线方程；‎ ‎（II）是否存在平行于OA（O为坐标原点）的直线L，使得直线L与抛物线C有公共点，且直线OA与L的距离等于？若存在，求直线L的方程；若不存在，说明理由。‎ ‎（11年）11．设圆锥曲线I的两个焦点分别为F1，F2，若曲线I上存在点P满足：：=4：3:2，则曲线I的离心率等于 ‎ A． B． C． D．‎ ‎18．如图，直线l：y=x+b与抛物线C：x2=4y相切于点A。‎ ‎（I）求实数b的值；‎ ‎（11）求以点A为圆心，且与抛物线C的准线相切的圆的方程．‎ ‎（12年）5 已知双曲线-=1的右焦点为（3,0），则该双曲线的离心率等于 A B C D ‎ ‎7.直线x+-2=0与圆x2+y2=4相交于A,B两点，则弦AB的长度等于 ‎ A. B . C. D.1‎ ‎21.如图，等边三角形OAB的边长为，且其三个顶点均在抛物线E：x2=2py（p＞0）上。‎ （1） 求抛物线E的方程；‎ （2） 设动直线l与抛物线E相切于点P，与直线y=-1相交于点Q。证明以PQ为直径的圆恒过y轴上某定点。‎ ‎（13年）4．双曲线的顶点到其渐近线的距离等于（ ）‎ A． B． C．1 D．‎ ‎15．椭圆的左、右焦点分别为，焦距为．若直线与 椭圆的一个交点满足，则该椭圆的离心率等于 ‎ ‎20．如图，在抛物线的焦点为，准线与轴的交点为．点在抛物线上，以为圆心为半径作圆，设圆与准线的交于不同的两点．‎ ‎（1）若点的纵坐标为2，求；‎ ‎（2）若，求圆的半径．‎ ‎（14年）‎ 6. 已知直线过圆的圆心，且与直线垂直，则的方程是（ ）‎ 21. 已知曲线上的点到点的距离比它到直线的距离小2.‎ （1） 求曲线的方程；‎ （2） 曲线在点处的切线与轴交于点.直线分别与直线及轴交于点，以为直径作圆，过点作圆的切线，切点为，试探究：当点在曲线上运动（点与原点不重合）时，线段的长度是否发生变化？证明你的结论.‎