立体几何中的向量问题空间角与距离高考数学总复习高中数学课时训 10页

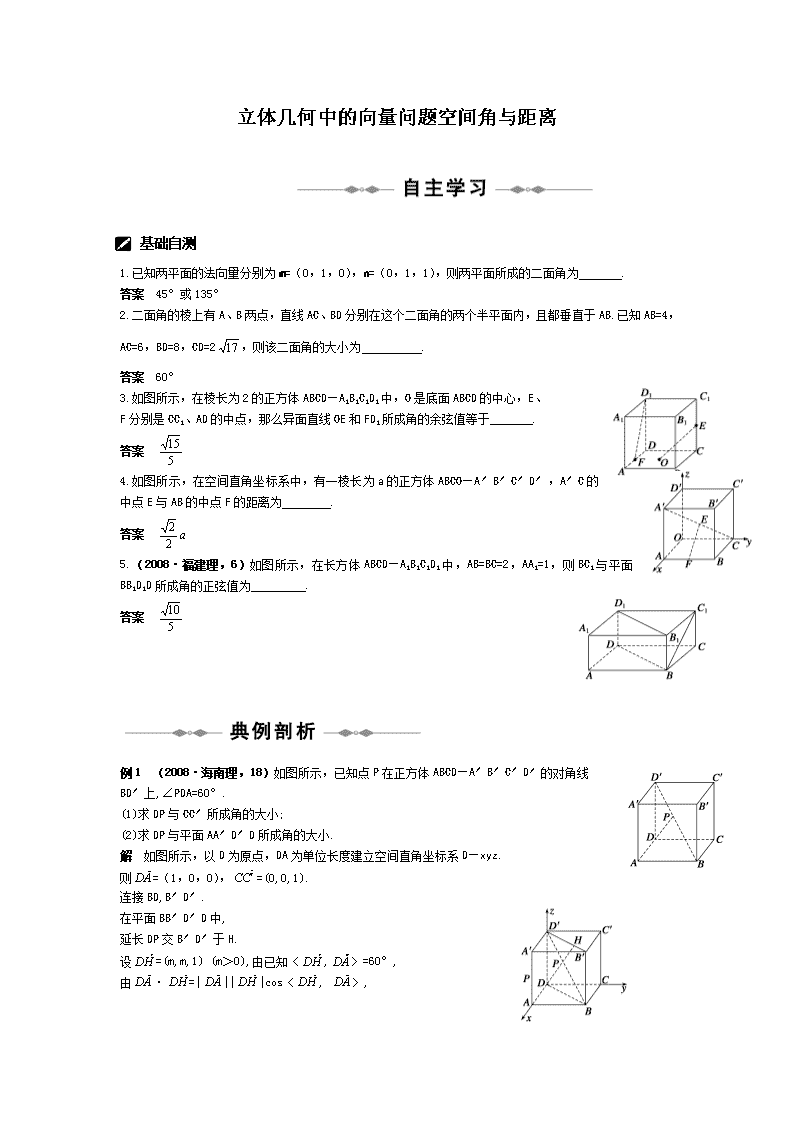
立体几何中的向量问题空间角与距离 基础自测 ‎1.已知两平面的法向量分别为m=（0，1，0），n=（0，1，1），则两平面所成的二面角为 .‎ 答案 45°或135°‎ ‎2.二面角的棱上有A、B两点，直线AC、BD分别在这个二面角的两个半平面内，且都垂直于AB.已知AB=4，AC=6，BD=8，CD=2，则该二面角的大小为 .‎ 答案 60°‎ ‎3.如图所示，在棱长为2的正方体ABCD—A1B1C1D1中，O是底面ABCD的中心，E、‎ F分别是CC1、AD的中点，那么异面直线OE和FD1所成角的余弦值等于 .‎ 答案 ‎ ‎4.如图所示，在空间直角坐标系中，有一棱长为a的正方体ABCO—A′B′C′D′，A′C的中点E与AB的中点F的距离为 .‎ 答案 ‎ ‎5.（2008·福建理，6）如图所示，在长方体ABCD—A1B1C1D1中，AB=BC=2，AA1=1，则BC1与平面BB1D1D所成角的正弦值为 .‎ 答案 ‎ 例1 （2008·海南理，18）如图所示，已知点P在正方体ABCD—A′B′C′D′的对角线 BD′上,∠PDA=60°.‎ ‎(1)求DP与CC′所成角的大小;‎ ‎(2)求DP与平面AA′D′D所成角的大小.‎ 解 如图所示，以D为原点，DA为单位长度建立空间直角坐标系D—xyz.‎ 则=（1，0，0），=(0,0,1).‎ 连接BD,B′D′.‎ 在平面BB′D′D中,‎ 延长DP交B′D′于H.‎ 设=(m,m,1) (m＞0),由已知〈,〉=60°,‎ 由·=||||cos〈, 〉,‎ 可得2m=.‎ 解得m=,所以=（,,1）.‎ ‎(1)因为cos〈,〉==,‎ 所以〈,〉=45°,‎ 即DP与CC′所成的角为45°.‎ ‎(2)平面AA′D′D的一个法向量是=(0,1,0).‎ 因为cos〈,〉==,‎ 所以〈,〉=60°,‎ 可得DP与平面AA′D′D所成的角为30°.‎ 例2 在三棱锥S—ABC中，△ABC是边长为4的正三角形，平面SAC⊥平面ABC，SA=SC=2，M、N分别为AB、SB的中点，如图所示. ‎ 求点B到平面CMN的距离.‎ 解 取AC的中点O，连接OS、OB.‎ ‎∵SA=SC，AB=BC，‎ ‎∴AC⊥SO，AC⊥BO.‎ ‎∵平面SAC⊥平面ABC，‎ 平面SAC∩平面ABC=AC，‎ ‎∴SO⊥平面ABC，∴SO⊥BO.‎ 如图所示，建立空间直角坐标系O—xyz，‎ 则B（0，2，0），C（-2，0，0），S（0，0，2），‎ M（1，，0），N（0，，）.‎ ‎∴=（3，，0），=（-1，0，），=（-1，，0）.‎ 设n=(x,y,z)为平面CMN的一个法向量，‎ 则，取z=1，‎ 则x=,y=-,∴n=（，-，1）.‎ ‎∴点B到平面CMN的距离d=.‎ 例3 （16分）如图所示，四棱锥P—ABCD中，底面ABCD是矩形，PA⊥底面ABCD，PA=AB=1，AD=，点F是PB的中点，点E在边BC上移动.‎ ‎（1）点E为BC的中点时，试判断EF与平面PAC的位置关系，并说明理由；‎ ‎（2）求证：无论点E在BC边的何处，都有PE⊥AF；‎ ‎（3）当BE为何值时，PA与平面PDE所成角的大小为45°.‎ ‎（1）解 当点E为BC的中点时，EF与平面PAC平行.‎ ‎∵在△PBC中，E、F分别为BC、PB的中点，∴EF∥PC.‎ 又EF平面PAC，而PC平面PAC，‎ ‎∴EF∥平面PAC. 4分 ‎（2）证明 以A为坐标原点建立如图所示的空间直角坐标系 则P（0，0，1），B（0，1，0），‎ F（0，，），D（，0，0）.‎ 设BE=x，则E（x，1，0），‎ ‎·=（x，1，-1）·（0，，）=0，‎ ‎∴PE⊥AF. 10分 ‎（3）解 设平面PDE的法向量为m=(p,q,1),‎ 由（2）知=（，0，-1），=（x，1，-1）‎ 由，得m=. 12分 而=（0，0，1），依题意PA与平面PDE所成角为45°,‎ ‎∴sin45°==，‎ ‎∴=, 14分 得BE=x=-或BE=x=+＞（舍去）.‎ 故BE=-时，PA与平面PDE所成角为45°. 16分 ‎1.如图所示，AF、DE分别是⊙O、⊙O1的直径，AD与两圆所在的平面均垂直，AD=8.BC是⊙O的直径，AB=AC=6，‎ OE∥AD.‎ ‎（1）求二面角B-AD-F的大小；‎ ‎（2）求直线BD与EF所成的角的余弦值.‎ 解 （1）∵AD与两圆所在的平面均垂直，‎ ‎∴AD⊥AB，AD⊥AF，‎ 故∠BAF是二面角B—AD—F的平面角.‎ 依题意可知，ABFC是正方形，‎ ‎∴∠BAF=45°.‎ 即二面角B—AD—F的大小为45°;‎ ‎（2）以O为原点，CB、AF、OE所在直线为坐标轴，建立空间直角坐标系（如图所示），‎ 则O（0，0，0），‎ A（0，-3，0），B（3，0，0），D（0，-3，8），‎ E（0，0，8），F（0，3，0），‎ ‎∴=（-3，-3，8），=（0，3，-8）.‎ cos〈,〉= ==-.‎ 设异面直线BD与EF所成角为，则 cos=|cos〈,〉|=.‎ 即直线BD与EF所成的角的余弦值为.‎ ‎2.已知：正四棱柱ABCD—A1B1C1D1中，底面边长为2，侧棱长为4，E、F分别为棱AB、BC的中点.‎ ‎（1）求证：平面B1EF⊥平面BDD1B1；‎ ‎（2）求点D1到平面B1EF的距离.‎ ‎（1）证明 建立如图所示的空间直角坐标系，则D（0，0，0），‎ B（2，2，0），E（2，，0），‎ F（，2，0），D1（0，0，4），‎ B1（2，2，4）.‎ ‎=（-，，0），=（2，2，0），=（0，0，4），‎ ‎∴·=0，·=0.‎ ‎∴EF⊥DB，EF⊥DD1，DD1∩BD=D，‎ ‎∴EF⊥平面BDD1B1.‎ 又EF平面B1EF，∴平面B1EF⊥平面BDD1B1.‎ ‎（2）解 由（1）知=（2，2，0），‎ ‎=（-，，0），=（0，-，-4）.‎ 设平面B1EF的法向量为n,且n=(x,y,z)‎ 则n⊥,n⊥‎ 即n·=（x，y，z）·（-，，0）=-x+y=0，‎ n·=（x，y，z）·（0，-，-4）=-y-4z=0，‎ 令x=1,则y=1,z=-,∴n=(1,1,- )‎ ‎∴D1到平面B1EF的距离 d===.‎ ‎3.如图所示，在四棱锥P—ABCD中，底面ABCD为矩形，侧棱PA⊥底面ABCD，AB=， ‎ BC=1，PA=2，E为PD的中点.‎ ‎（1）求直线AC与PB所成角的余弦值；‎ ‎（2）在侧面PAB内找一点N，使NE⊥平面PAC，并求出N点到AB和AP的距离.‎ 解 方法一 （1）建立如图所示的空间直角坐标系，‎ 则A、B、C、D、P、E的坐标为A（0，0，0），B（，0，0）、C（，1，0）、D（0，1，0）、P（0，0，2）、‎ E(0，，1)，‎ 从而=（，1，0），=（，0，-2）.‎ 设与的夹角为，‎ 则cos===，‎ ‎∴AC与PB所成角的余弦值为.‎ ‎（2）由于N点在侧面PAB内，故可设N点坐标为（x,0,z）,则=（-x，，1-z），由NE⊥平面PAC可得 ‎，即,‎ 化简得,∴‎ 即N点的坐标为（，0，1），从而N点到AB、AP的距离分别为1，.‎ 方法二 （1）设AC∩BD=O，‎ 连接OE，AE，BD，‎ 则OE∥PB，‎ ‎∴∠EOA即为AC与PB所成的角或其补角.‎ 在△AOE中，AO=1，OE=PB=，AE=PD=，‎ ‎∴由余弦定理得 cos∠EOA=,‎ 即AC与PB所成角的余弦值为.‎ ‎(2)在平面ABCD内过D作AC的垂线交AB于F,则∠ADF=.连接PF,则在Rt△ADF中,‎ DF==,‎ AF=AD·tan∠ADF=.‎ 设N为PF的中点，连接NE，则NE∥DF.‎ ‎∵DF⊥AC，DF⊥PA，‎ ‎∴DF⊥平面PAC，从而NE⊥平面PAC.‎ ‎∴N点到AB的距离为AP=1，‎ N点到AP的距离为AF=.‎ 一、填空题 ‎1.在正方体ABCD—A1B1C1D1中,M是AB的中点,则sin〈,〉的值等于 .‎ 答案 ‎ ‎2.正方体ABCD—A1B1C1D1的棱长为1，O是A1C1的中点，则点O到平面ABC1D1的距离为 .‎ 答案 ‎ ‎3.（2008·全国Ⅰ理，11）已知三棱柱ABC—A1B1C1的侧棱与底面边长都相等，A1在底面ABC内的射影为△ABC的中心，则AB1与底面ABC所成角的正弦值等于 .‎ 答案 ‎ ‎4.P是二面角—AB—棱上的一点，分别在、平面上引射线PM、PN，如果∠BPM=∠BPN=45°，∠MPN=60°，那么二面角—AB—的大小为 .‎ 答案 90°‎ ‎5.正方体ABCD—A1B1C1D1的棱长为1，E、F分别为BB1、CD的中点，则点F到平面A1D1E的距离为 .‎ 答案 ‎ ‎6.如图所示，在三棱柱ABC—A1B1C1中，AA1⊥底面ABC，AB=BC=AA1，∠ABC=90°，‎ 点E、F分别是棱AB、BB1的中点，则直线EF和BC1所成的角是 .‎ 答案 60°‎ ‎7.如图所示，已知正三棱柱ABC—A1B1C1的所有棱长都相等，D是A1C1的中点，则直线AD与 平面B1DC所成角的正弦值为 .‎ 答案 ‎ ‎8.正四棱锥S—ABCD中,O为顶点在底面上的射影,P为侧棱SD的中点,且SO=OD,则直线BC与平面PAC所成的角是 .‎ 答案 30°‎ 二、解答题 ‎9.如图所示，在几何体ABCDE中，△ABC是等腰直角三角形，∠ABC=90°，‎ BE和CD都垂直于平面ABC，且BE=AB=2，CD=1，点F是AE的中点.‎ 求AB与平面BDF所成角的正弦值.‎ 解 以点B为原点，BA、BC、BE所在的直线分别为x，y，z轴，建立如图所示的空间直角坐标系，则 B（0，0，0），A（2，0，0），C（0，2，0），D（0，2，1），E（0，0，2），F（1，0，1）.‎ ‎∴=（0，2，1），=（1，-2，0）.‎ 设平面BDF的一个法向量为 n=（2，a，b），‎ ‎∵n⊥，n⊥，‎ ‎∴‎ 即 解得a=1，b=-2.∴n=（2，1，-2）.‎ 设AB与平面BDF所成的角为，则法向量n与的夹角为-，‎ ‎∴cos（-）===,‎ 即sin=,故AB与平面BDF所成角的正弦值为.‎ ‎10.在五棱锥P—ABCDE中，PA=AB=AE=2a，PB=PE=2a，BC=DE=a，∠EAB=∠ABC=‎ ‎∠DEA=90°.‎ ‎（1）求证：PA⊥平面ABCDE；‎ ‎（2）求二面角A—PD—E的余弦值.‎ ‎（1）证明 以A点为坐标原点，以AB、AE、AP所在直线分别为x、y、z轴，建立空间直角坐标系A—xyz，则由已知得 A（0，0，0），P（0，0，2a），‎ B（2a，0，0），C（2a，a，0），‎ D（a，2a，0），E（0，2a，0）.‎ ‎∴=（0，0，2a），=（2a，0，0），=（0，2a，0），‎ ‎∴·=0·2a+0·0+2a·0=0，‎ ‎∴⊥.同理⊥.‎ 又∵AB∩AE=A，∴PA⊥平面ABCDE.‎ ‎（2）解 设平面PAD的法向量为m=(1,y,z),‎ 则m·=0，得a+2ay=0，∴y=-.‎ 又m·=0，得2az=0，∴z=0.‎ ‎∴m=（1，-，0）.‎ 再设平面PDE的法向量为n=(x,1,z),‎ 而=（a，0，0），=（a，2a，-2a），‎ 则n·=0，得ax=0，∴x=0.‎ 又n·=0，得ax+2a-2az=0，∴z=1.‎ ‎∴n=（0，1，1）.‎ 令二面角A—PD—E的平面角为，‎ 则cos=-==，‎ 故二面角A—PD—E的余弦值是.‎ ‎11.如图所示，在三棱锥P—ABC中，AB⊥BC，AB=BC=kPA，点O、D分别是AC、PC的中点，‎ OP⊥底面ABC.‎ ‎（1）若k=1，试求异面直线PA与BD所成角余弦值的大小；‎ ‎（2）当k取何值时，二面角O—PC—B的大小为？‎ 解 ∵OP⊥平面ABC，又OA=OC，AB=BC，‎ 从而OA⊥OB，OB⊥OP，OA⊥OP，‎ 以O为原点，建立如图所示空间直角坐标系O—xyz.‎ ‎（1）设AB=a，则PA=a，PO=a，‎ A（a，0，0），B（0，a，0），‎ C（-a，0，0），P（0，0，a），‎ 则D（-a，0，a）.‎ ‎∵=(a，0，-a )，=(-a，-a，a)，‎ ‎∴cos〈,〉===-,‎ 则异面直线PA与BD所成角的余弦值的大小为.‎ ‎（2）设AB=a，OP=h，∵OB⊥平面POC，‎ ‎∴=(0，a，0)为平面POC的一个法向量.‎ 不妨设平面PBC的一个法向量为n=（x，y，z），‎ ‎∵A(a，0，0)，B(0，a，0)，C(-a，0，0)，P(0，0，h)，‎ ‎∴=(-a,- a,0),=(- a,0,-h),‎ 由 不妨令x=1，则y=-1，z=-，‎ 即n=(1,-1,- ),则cos=‎ ‎==2+=4h=a,‎ ‎∴PA===a,‎ 而AB=kPA,∴k=.‎ 故当k=时,二面角O—PC—B的大小为.‎ ‎12.(2008·湛江模拟)如图所示，已知长方体ABCD—A1B1C1D1中，AB=BC=2，AA1=4，‎ E是棱CC1上的点，且BE⊥B1C.‎ ‎（1）求CE的长；‎ ‎（2）求证：A1C⊥平面BED；‎ ‎（3）求A1B与平面BDE所成角的正弦值.‎ ‎（1）解 如图所示，以D为原点，DA、DC、DD1所在直线分别为x、y、z轴建立空间直角坐标系D—xyz. ‎ ‎∴D（0，0，0），A（2，0，0），B（2，2，0），‎ C（0，2，0），A1（2，0，4），‎ B1（2，2，4），C1（0，2，4），D1（0，0，4）.‎ 设E点坐标为（0，2，t），则=（-2，0，t），=（-2，0，-4）.‎ ‎∵BE⊥B1C，‎ ‎∴·=4+0-4t=0.∴t=1，故CE=1.‎ ‎（2）证明 由（1）得，E（0，2，1），=（-2，0，1），‎ 又=（-2，2，-4），=（2，2，0），‎ ‎∴·=4+0-4=0，‎ 且·=-4+4+0=0.‎ ‎∴⊥且⊥，即A1C⊥DB，A1C⊥BE，‎ 又∵DB∩BE=B，∴A1C⊥平面BDE.‎ 即A1C⊥平面BED.‎ ‎（3）解 由（2）知=（-2，2，-4）是平面BDE的一个法向量.又=（0，2，-4）,‎ ‎∴cos〈,〉==.‎ ‎∴A1B与平面BDE所成角的正弦值为.‎