山东卷高考试题数学文Word版有答案 12页

本资料来源于《七彩教育网》http://www.7caiedu.cn ‎2009年普通高等学校招生全国统一考试(山东卷)‎ 文科数学 本试卷分第Ⅰ卷和第Ⅱ卷两部分,共4页，满分150分，考试时间120分钟。考试结束后,将本试卷和答题卡一并交回.‎ 注意事项：‎ ‎1. 答题前，考生务必用0.5毫米黑色签字笔将自己的姓名、座号、准考证号、县区和科类填写在答题卡和试卷规定的位置上.，并将准考证号条形码粘贴在答题卡上指定位置。‎ ‎2. 第Ⅰ卷每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号，答案不能答在试卷上。‎ ‎3. 第Ⅱ卷必须用0.5毫米黑色签字笔在答题卡各题的答题区域内作答;不能写在试题卷上; 如需改动，先画掉原来的答案,然后再写上新的答案;不能使用涂改液、胶带纸,修正带,不按以上要求作答的答案无效。‎ ‎4. 填空题请直接填写答案,解答题应写出文字说明,证明过程或演算步骤.。‎ 参考公式：‎ 柱体的体积公式V=Sh，其中S是柱体的底面积，h是锥体的高。‎ 锥体的体积公式V=，其中S是锥体的底面积，h是锥体的高。‎ ‎ 第Ⅰ卷(共60分)‎ 一、选择题：本大题共12小题，每小题5分，共50分。在每小题给出的四个选项中，只有一项是符合题目要求的。‎ ‎1.集合,,若,则的值为( )‎ A.0 B‎.1 C.2 D.4 ‎ ‎2.复数等于（ ）. ‎ A． B. C. D. ‎ ‎3.将函数的图象向左平移个单位, 再向上平移1个单位,所得图象的函数解析式是( ). ‎ A. B. C. D. 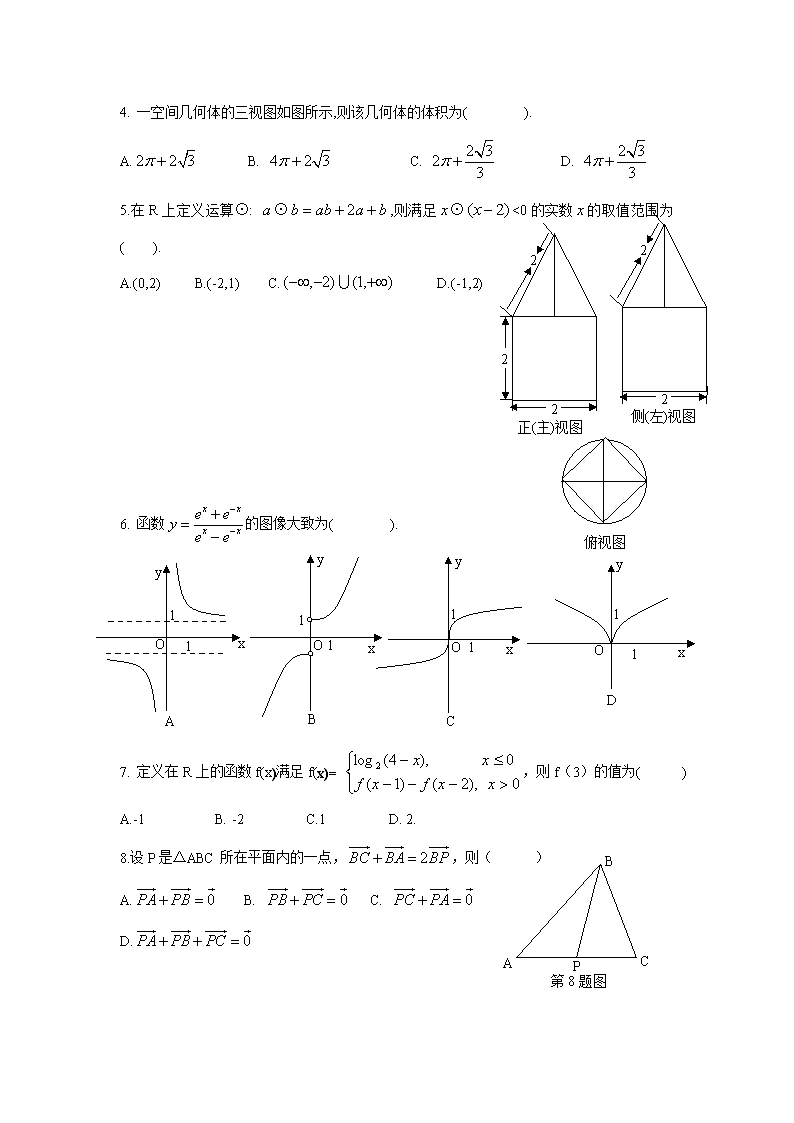‎ ‎4. 一空间几何体的三视图如图所示,则该几何体的体积为( ).‎ A. B. C. D. ‎ ‎2 ‎ ‎2 ‎ 侧(左)视图 ‎ ‎2 ‎ ‎2 ‎ ‎2 ‎ 正(主)视图 ‎ ‎5.在R上定义运算⊙: ⊙,则满足⊙<0的实数的取值范围为( ).‎ A.(0,2) B.(-2,1) C. D.(-1,2) ‎ 俯视图 ‎ ‎6. 函数的图像大致为( ). ‎ ‎1 ‎ x ‎ y ‎ ‎1 ‎ O ‎ A ‎ x ‎ y ‎ O ‎ ‎1 ‎ ‎1 ‎ B ‎ x ‎ y ‎ O ‎ ‎1 ‎ ‎1 ‎ C ‎ x ‎ y ‎ ‎1 ‎ ‎1 ‎ D ‎ O ‎ ‎ ‎ ‎7. 定义在R上的函数f(x)满足f(x)= ，则f（3）的值为( )‎ A.-1 B. ‎-2 C.1 D. 2. ‎ A ‎ B ‎ C ‎ P ‎ 第8题图 ‎ ‎8.设P是△ABC所在平面内的一点，，则（　　　）‎ A. B. C. ‎ D.‎ ‎9. 已知α，β表示两个不同的平面，m为平面α内的一条直线，则“”是“”的( )‎ A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 ‎ ‎10. 设斜率为2的直线过抛物线的焦点F,且和轴交于点A,若△OAF(O为坐标原点)的面积为4,则抛物线方程为( ). ‎ A. B. C. D. ‎ ‎11.在区间上随机取一个数x，的值介于0到之间的概率为( ).‎ A. B. C. D. ‎ ‎12. 已知定义在R上的奇函数，满足,且在区间[0,2]上是增函数,则( ). ‎ A. B. ‎ C. D. ‎ 第卷 二、填空题：本大题共4小题，每小题4分，共16分。‎ ‎13.在等差数列中,,则.13.‎ ‎14.若函数f(x)=a-x-a(a>0且a1)有两个零点，则实数a的取值范围是 . ‎ 开始 ‎ S=0,T=0,n=0 ‎ T>S ‎ S=S+5 ‎ n=n+2 ‎ T=T+n ‎ 输出T ‎ 结束 ‎ 是 ‎ 否 ‎ ‎15.执行右边的程序框图，输出的T= . ‎ ‎16.某公司租赁甲、乙两种设备生产A,B两类产品,甲种设备每天能 生产A类产品5件和B类产品10件,乙种设备每天能生产A类产 品6件和B类产品20件.已知设备甲每天的租赁费为200元,‎ 设备乙每天的租赁费为300元,现该公司至少要生产A类产品50件 ‎,B类产品140件,所需租赁费最少为__________元. ‎ 三、解答题：本大题共6小题，共74分。‎ ‎17.(本小题满分12分)设函数f(x)=2在处取最小值.‎ (1) 求.的值;‎ (2) 在ABC中,分别是角A,B,C的对边,已知,求角C..‎ ‎18.（本小题满分12分）‎ ‎ 如图，在直四棱柱ABCD-ABCD中，底面ABCD为等腰梯形，AB//CD，AB=4, BC=CD=2, AA=2, E、E分别是棱AD、AA的中点. ‎ E ‎ A ‎ B ‎ C ‎ F ‎ E1 ‎ A1 ‎ B1 ‎ C1 ‎ D1 ‎ D ‎ （1） 设F是棱AB的中点,证明：直线EE//平面FCC；‎ （2） 证明:平面D1AC⊥平面BB1C1C.‎ ‎19. （本小题满分12分）‎ ‎ 一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):‎ 轿车A 轿车B 轿车C 舒适型 ‎100‎ ‎150‎ z 标准型 ‎300‎ ‎450‎ ‎600‎ 按类型分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.‎ （1） 求z的值. ‎ （2） 用分层抽样的方法在C类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;‎ （3） 用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4, 8.6, 9.2, 9.6, 8.7, 9.3, 9.0, 8.2.把这8辆轿车的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.‎ ‎20.（本小题满分12分）‎ 等比数列{}的前n项和为， 已知对任意的 ，点，均在函数且均为常数)的图像上. ‎ ‎（1）求r的值； ‎ ‎（11）当b=2时，记 求数列的前项和 ‎21.（本小题满分12分）‎ 已知函数,其中 ‎ （1） 当满足什么条件时,取得极值?‎ （2） 已知,且在区间上单调递增,试用表示出的取值范围.‎ ‎22. （本小题满分14分）‎ 设,在平面直角坐标系中,已知向量,向量,,动点的轨迹为E.‎ ‎（1）求轨迹E的方程,并说明该方程所表示曲线的形状;‎ ‎（2）已知,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且(O为坐标原点),并求出该圆的方程;‎ ‎(3)已知,设直线与圆C:(1