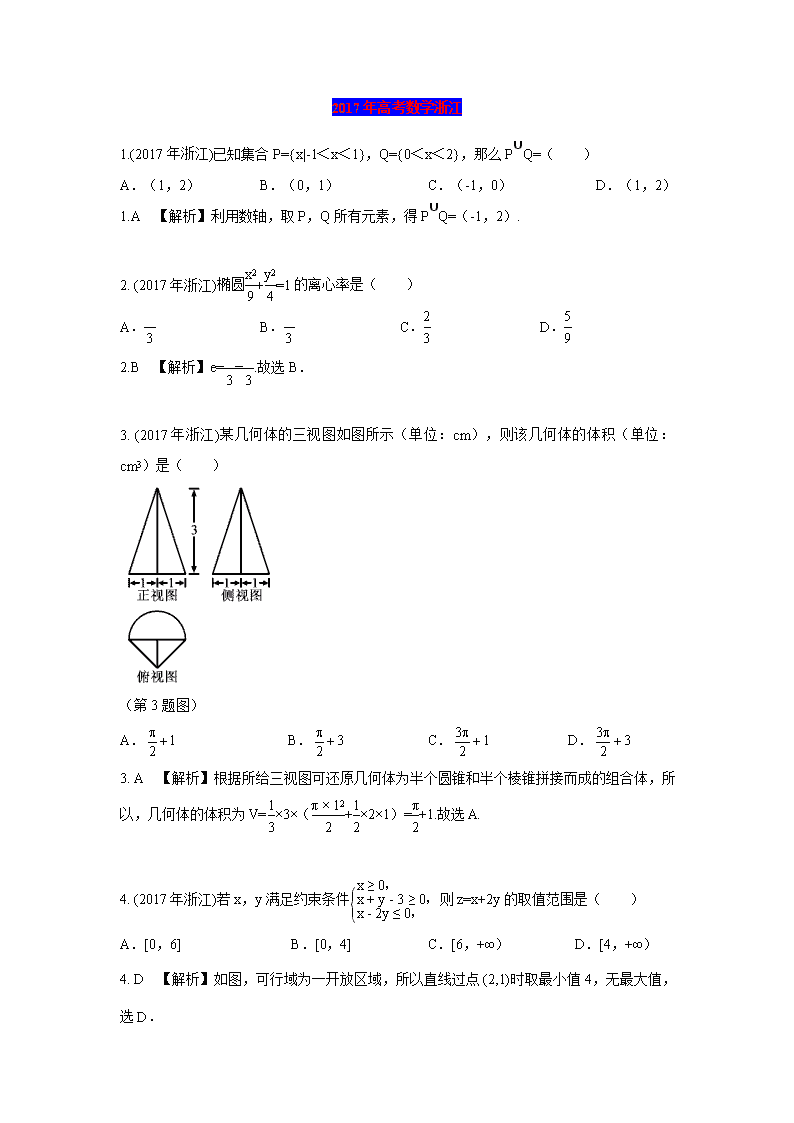高考数学浙江试题及解析 10页

‎2017年高考数学浙江 ‎1.(2017年浙江)已知集合P={x|-1＜x＜1}，Q={0＜x＜2}，那么P∪Q=（ ）‎ A．（1，2） B．（0，1） C．（-1，0） D．（1，2）‎ ‎1.A 【解析】利用数轴，取P，Q所有元素，得P∪Q=（-1，2）.‎ ‎2. (2017年浙江)椭圆+=1的离心率是（ ）‎ A． B． C． D． ‎2.B 【解析】e==.故选B．‎ ‎3. (2017年浙江)某几何体的三视图如图所示（单位：cm），则该几何体的体积（单位：cm3）是（ ）‎ ‎（第3题图）‎ A． B． C． D．‎ ‎3. A 【解析】根据所给三视图可还原几何体为半个圆锥和半个棱锥拼接而成的组合体，所以，几何体的体积为V=×3×（+×2×1）=+1.故选A.‎ ‎4. (2017年浙江)若x，y满足约束条件则z=x+2y的取值范围是（ ）‎ A．[0，6] B．[0，4] C．[6，+∞） D．[4，+∞）‎ ‎4. D 【解析】如图，可行域为一开放区域，所以直线过点时取最小值4，无最大值，选D．‎ ‎5. (2017年浙江)若函数f(x)=x2+ ax+b在区间[0，1]上的最大值是M，最小值是m，则M – m（ ）‎ A．与a有关，且与b有关 B．与a有关，但与b无关 C．与a无关，且与b无关 D．与a无关，但与b有关 ‎5. B 【解析】因为最值f（0）=b，f（1）=1+a+b，f（-）=b-中取，所以最值之差一定与b无关.故选B.‎ ‎6. (2017年浙江)已知等差数列{an}的公差为d，前n项和为Sn，则“d>0”是“S4 + S6>2S5”的（ ）‎ A．充分不必要条件 B．必要不充分条件 C．充分必要条件 D．既不充分也不必要条件 ‎6. C 【解析】由S4 + S6-2S5=10a1+21d-2（5a1+10d）=d，可知当d＞0时，有S4+S6-2S5＞0，即S4 + S6>2S5，反之，若S4 + S6>2S5，则d＞0，所以“d>0”是“S4 + S6>2S5”的充要条件，选C．‎ ‎7. (2017年浙江)函数y=f(x)的导函数y=f′（x）的图象如图所示，则函数y=f(x)的图象可能是（ ）‎ ‎（第7题图）‎ ‎7. D 【解析】原函数先减再增，再减再增，且x=0位于增区间内.故选D.‎ ‎8. (2017年浙江)已知随机变量ξi满足P（ξi=1）=pi，P（ξi=0）=1–pi，i=1，2． 若00．‎ 假设n=k时，xk>0，‎ 那么n=k+1时，若xk+1≤0，则0＜xk= xk+1+ln（1+ xk+1）≤0，矛盾，故xk+1＞0． ‎ 因此xn＞0（n∈N*）．‎ 所以xn=xn+1+ln（1+xn+1）＞xn+1，‎ 因此0＜xn+1＜xn（n∈N*）．‎ ‎（2）由xn=xn+1+ln（1+xn+1），‎ 得xnxn+1-4xn+1+2xn=xn+12-2xn+1+（xn+1+2）ln（1+xn+1）.‎ 记函数f（x）=x2-2x+（x+2）ln（1+x）（x≥0），‎ f′（x）=+ln（1+x）＞0（x＞0），‎ 函数f（x）在[0，+∞]上单调递增，所以f（x）≥f（0）=0，‎ 因此xn+12-2xn+1+（xn+1+2）ln（1+xn+1）=f（xn+1）≥0，‎ 故2xn+1-xn≤（n∈N*）．‎ ‎（3）因为xn=xn+1+ln（1+xn+1）≤xn+1+xn+1=2xn+1，‎ 所以xn≥，‎ 由≥2xn+1-xn，‎ 得-≥2（-）＞0，‎ 所以-≥2（-）≥…≥2n-1（-）=2n-2，‎ 故xn≤．‎ 综上，≤xn≤（n∈N*）．‎