- 3.52 MB
- 2021-05-13 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
1.【2017 山东,理 19】已知{xn}是各项均为正数的等比数列,且 x1+x2=3,x3-x2=2
(Ⅰ)求数列{xn}的通项公式;
(Ⅱ)如图,在平面直角坐标系 xOy 中,依次连接点 P1(x1, 1),P2(x2, 2)…Pn+1(xn+1, n+1)得到折线 P1
P2…Pn+1,求由该折线与直线 y=0, 所围成的区域的面积 .
【答案】(I) (II)
【解析】试题分析:(I)依题意布列 和公比的方程组.
(II)过 …… 向轴作垂线,垂足分别为 …… ,
nT
12 .n
nx −= (2 1) 2 1.2
n
n
nT
− × +=
1 2 3, , ,P P P 1nP + 1 2 3, , ,Q Q Q 1nQ +
1 1nx x x x += =,
1x
由(I)得
记梯形 的面积为 .
由题意 ,
所以
……+
= ……+ ①
又 ……+ ②
①-②得
=
所以
【考点】1.等比数列的通项公式;2.等比数列的求和;3.“错位相减法”.
2. 【 2017 北 京 , 理 20 】 设 和 是 两 个 等 差 数 列 , 记
,
其中 表示 这个数中最大的数.
(Ⅰ)若 , ,求 的值,并证明 是等差数列;
(Ⅱ)证明:或者对任意正数 ,存在正整数 ,当 时, ;或者存在正整
数 ,使得 是等差数列.
【答案】(Ⅰ)详见解析;(Ⅱ)详见解析.
【解析】
1 1
1 2 2 2 .n n n
n nx x − −
+ − = − =
1 1n n n nP P Q Q+ + nb
1 2( 1) 2 (2 1) 22
n n
n
n nb n− −+ += × = + ×
1 2 3nT b b b= + + + nb
1 0 13 2 5 2 7 2−× + × + × + 3 2(2 1) 2 (2 1) 2n nn n− −− × + + ×
0 1 22 3 2 5 2 7 2nT = × + × + × + 2 1(2 1) 2 (2 1) 2n nn n− −− × + + ×
1 2 1 13 2 (2 2 ...... 2 ) (2 1) 2n n
nT n− − −− = × + + + + − + ×
1
13 2(1 2 ) (2 1) 2 .2 1 2
n
nn
−
−−+ − + ×−
(2 1) 2 1.2
n
n
nT
− × +=
{ }na { }nb
1 1 2 2max{ , , , }n n nc b a n b a n b a n= − − ⋅⋅⋅ − ( 1,2,3, )n = ⋅⋅⋅
1 2max{ , , , }sx x x⋅⋅⋅ 1 2, , , sx x x⋅⋅⋅
na n= 2 1nb n= − 1 2 3, ,c c c { }nc
M m n m≥ nc Mn
>
m 1 2, , ,m m mc c c+ + ⋅⋅⋅
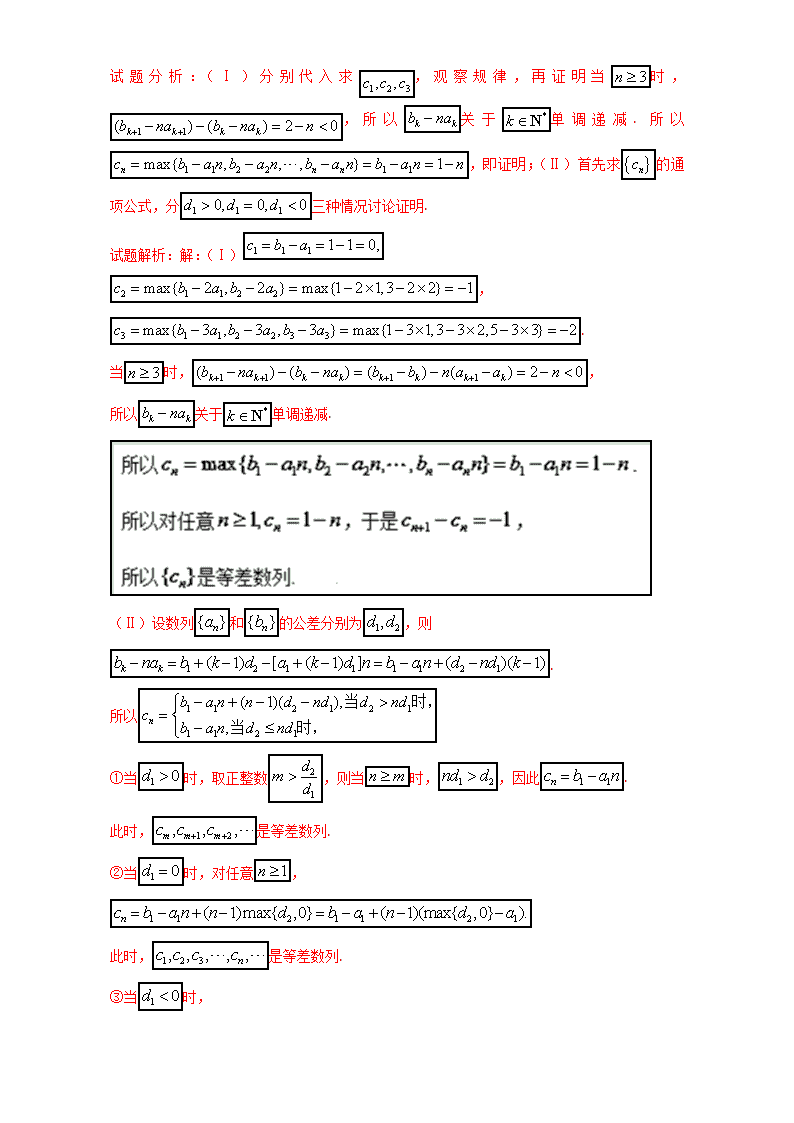
试 题 分 析 : ( Ⅰ ) 分 别 代 入 求 , 观 察 规 律 , 再 证 明 当 时 ,
, 所 以 关 于 单 调 递 减 . 所 以
,即证明;(Ⅱ)首先求 的通
项公式,分 三种情况讨论证明.
试题解析:解:(Ⅰ)
,
.
当 时, ,
所以 关于 单调递减.
(Ⅱ)设数列 和 的公差分别为 ,则
.
所以
①当 时,取正整数 ,则当 时, ,因此 .
此时, 是等差数列.
②当 时,对任意 ,
此时, 是等差数列.
③当 时,
1 2 3, ,c c c 3n ≥
1 1( ) ( ) 2 0k k k kb na b na n+ +− − − = − < k kb na− *k ∈N
1 1 2 2 1 1max{ , , , } 1n n nc b a n b a n b a n b a n n= − − − = − = − { }nc
1 1 10, 0, 0d d d> = <
1 1 1 1 1 0,c b a= − = − =
2 1 1 2 2max{ 2 , 2 } max{1 2 1,3 2 2} 1c b a b a= − − = − × − × = −
3 1 1 2 2 3 3max{ 3 , 3 , 3 } max{1 3 1,3 3 2,5 3 3} 2c b a b a b a= − − − = − × − × − × = −
3n ≥ 1 1 1 1( ) ( ) ( ) ( ) 2 0k k k k k k k kb na b na b b n a a n+ + + +− − − = − − − = − <
k kb na− *k ∈N
{ }na { }nb 1 2,d d
1 2 1 1 1 1 2 1( 1) [ ( 1) ] ( )( 1)k kb na b k d a k d n b a n d nd k− = + − − + − = − + − −
1 1 2 1 2 1
1 1 2 1
( 1)( ),
,n
b a n n d nd d ndc
b a n d nd
− + − − >= − ≤
当 时,
当 时,
1 0d > 2
1
dm d
> n m≥ 1 2nd d> 1 1nc b a n= −
1 2, , ,m m mc c c+ +
1 0d = 1n ≥
1 1 2 1 1 2 1( 1)max{ ,0} ( 1)(max{ ,0} ).nc b a n n d b a n d a= − + − = − + − −
1 2 3, , , , ,nc c c c
1 0d <
当 时,有 .
所以
对任意正数 ,取正整数 ,
故当时, .
【考点】1.新定义;2.数列的综合应用;3.推理与证明.
3.【2017 天津,理 18】已知 为等差数列,前 n 项和为 , 是首项为 2 的
等比数列,且公比大于 0, , , .
(Ⅰ)求 和 的通项公式;
(Ⅱ)求数列 的前 n 项和 .
【答案】 (1) . .(2) .
【解析】
试题分析:根据等差数列和等比数列通项公式及前项和公式列方程求出等差数列首项 和公差
及等比数列的公比,写出等差数列和等比孰劣的通项公式,利用错位相减法求出数列的和,
要求计算要准确.
试题解析:(I)设等差数列 的公差为 ,等比数列 的公比为.
由已知 ,得 ,而 ,所以 .
又因为 ,解得 .所以, .
由 ,可得 ①.
2
1
dn d
> 1 2nd d<
1 1 2 1 1 2
1 1 1 2
( 1)( ) ( )nc b a n n d nd b dn d d a dn n n
− + − − −= = − + − + +
1 1 1 2 1 2( ) | |.n d d a d b d≥ − + − + − −
M 1 2 1 1 2 2
1 1
| |max{ , }M b d a d d dm d d
+ − + − −> −
nc Mn
>
{ }na ( )nS n ∗∈N { }nb
2 3 12b b+ = 3 4 12b a a= − 11 411S b=
{ }na { }nb
2 2 1{ }n na b − ( )n ∗∈N
3 2na n= − 2n
nb = 13 2 843 3
n
n
nT +−= × +
1a
d
{ }na d { }nb
2 3 12b b+ = 2
1( ) 12b q q+ = 1 2b = 2 6 0q q+ − =
0q > 2q = 2n
nb =
3 4 12b a a= − 13 8d a− =
由 ,可得 ②,
联立①②,解得 , ,由此可得 .
所以,数列 的通项公式为 ,数列 的通项公式为 .
(II)解:设数列 的前项和为 ,
由 , ,有 ,
故 ,
,
上述两式相减,得
得 .
所以,数列 的前项和为 .
【考点】等差数列、等比数列、数列求和
4. 【 2017 浙 江 , 22 】 ( 本 题 满 分 15 分 ) 已 知 数 列 {xn} 满 足 : x1=1 , xn=xn+1+ln(1+xn+1)
( ).
证明:当 时,
(Ⅰ)0<xn+1<xn;
(Ⅱ)2xn+1− xn≤ ;
(Ⅲ) ≤xn≤ .
【答案】(Ⅰ)见解析;(Ⅱ)见解析;(Ⅲ)见解析.
【解析】
试 题 分 析 : ( Ⅰ ) 由 数 学 归 纳 法 证 明 ; ( Ⅱ ) 由 ( Ⅰ ) 得
11 4=11S b 1 5 16a d+ =
1 1a = 3d = 3 2na n= −
{ }na 3 2na n= − { }nb 2n
nb =
2 2 1{ }n na b − nT
2 6 2na n= − 1
2 1 2 4n
nb −
− = × 2 2 1 (3 1) 4n
n na b n− = − ×
2 32 4 5 4 8 4 (3 1) 4n
nT n= × + × + × + + − ×
2 3 4 14 2 4 5 4 8 4 (3 4) 4 (3 1) 4n n
nT n n += × + × + × + + − × + − ×
2 3 13 2 4 3 4 3 4 3 4 (3 1) 4n n
nT n +− = × + × + × + + × − − ×
1
1
12 (1 4 ) 4 (3 1) 41 4
(3 2) 4 8.
n
n
n
n
n
+
+
× −= − − − ×−
= − − × −
13 2 843 3
n
n
nT +−= × +
2 2 1{ }n na b −
13 2 843 3
nn +− × +
∗∈ Nn
∗∈ Nn
1
2
n nx x +
1
1
2n+ 2
1
2n+
, 构 造 函 数
, 由 函 数 单 调 性 可 证 ; ( Ⅲ ) 由
, 得 , 递 推 可 得
试题解析:(Ⅰ)用数学归纳法证明:
当 n=1 时,x1=1>0
假设 n=k 时,xk>0,那么 n=k+1 时,若 ,则 ,矛盾,故
.
因此 ,所以 ,因此
( Ⅱ ) 由 得
记函数
函数 f(x)在 0,+∞)上单调递增,所以 =0,
因 此 ,
(Ⅲ)因为 ,所以 得 ,
, ,
故 ,
【考点】不等式证明
5. 【 2017 江 苏 , 19 】 对 于 给 定 的 正 整 数 , 若 数 列 满 足
2
1 1 1 1 1 14 2 2 ( 2)ln(1 )n n n n n n n nx x x x x x x x+ + + + + +− + = − + + +
2( ) 2 ( 2)ln(1 )( 0)f x x x x x x= − + + + ≥
1 1 1 1ln(1 )n n n n nx x x x x+ + + += + + ≤ + 1
122
n n
n n
x x x x+
+≥ −
1 2
1 1 ( N )2 2nn nx n ∗
− −≤ ≤ ∈
0>nx
01 ≤+kx 0)1ln(0 11 ≤++=< ++ kkk xxx
01 >+kx
)(0 ∗∈> Nnxn 111 )1ln( +++ >++= nnnn xxxx )(0 1
∗
+ ∈<< Nnxx nn
111 )1ln( +++ >++= nnnn xxxx
2
1 1 1 1 1 14 2 2 ( 2)ln(1 )n n n n n n n nx x x x x x x x+ + + + + +− + = − + + +
2( ) 2 ( 2)ln(1 )( 0)f x x x x x x= − + + + ≥
( ) (0)f x f≥
2
1 1 1 1 12 ( 2)ln(1 ) ( ) 0n n n n nx x x x f x+ + + + +− + + + = ≥ 1
12 ( N )2
n n
n n
x xx x n ∗+
+ − ≤ ∈
1 1 1 1ln(1 )n n n n nx x x x x+ + + += + + ≤ + 1
1
2n nx −≥ 1
122
n n
n n
x x x x+
+≥ −
1
1 1 1 12( ) 02 2n nx x+
− ≥ − 〉 1 2
1 1
1 1 1 1 1 12( ) 2 ( ) 22 2 2
n n
n nx x x
− −
−
− ≥ − ≥ ⋅⋅⋅ − =
2
1
2n nx −≤ 1 2
1 1 ( N )2 2nn nx n ∗
− −≤ ≤ ∈
{ }na
对任意正整数 总成立,则称数列 是“ 数列”.
(1)证明:等差数列 是“ 数列”;
(2)若数列 既是“ 数列”,又是“ 数列”,证明: 是等差数列.
【答案】(1)见解析(2)见解析
【解析】证明:(1)因为 是等差数列,设其公差为 ,则 ,
从而,当 时,
,
所以 ,
因此等差数列 是“ 数列”.
,④
将③④代入②,得 ,其中 ,
所以 是等差数列,设其公差为 .
在①中,取 ,则 ,所以 ,
在①中,取 ,则 ,所以 ,
所以数列 是等差数列.
【考点】等差数列定义及通项公式
【名师点睛】证明 为等差数列的方法:
(1)用定义证明: 为常数);
1 1 1 1n k n k n n n k n ka a a a a a− − + − + + − ++ + + + + + +
2 nka= ( )n n k> { }na ( )P k
{ }na (3)P
{ }na (2)P (3)P { }na
{ }na d 1 ( 1)na a n d= + −
4n ≥ n k n ka a a− ++ = +1 1( 1) ( 1)n k d a n k d− − + + + −
12 2( 1) 2 na n d a= + − = 1,2,3,k =
n n n n n n na a a a a a a− − − + + ++ + =3 2 1 1 2 3+ + + 6
{ }na ( )3P
n n na a a+ + ++ = −2 3 14 1( )n na a− +
n n na a a− ++ =1 1 2 4n ≥
3 4 5, , ,a a a d'
4n = 2 3 5 6 44a a a a a+ + + = 2 3a a d'= −
3n = 1 2 4 5 34a a a a a+ + + = 1 2 2a a d'= −
{ }na
{ }na
1 (n na a d d+ − =
(2)用等差中项证明: ;
(3)通项法: 为的一次函数;
(4)前项和法:
6. 【 2016 高 考 新 课 标 2 理 数 】 为 等 差 数 列 的 前 项 和 , 且 记
,其中 表示不超过的最大整数,如 .
(Ⅰ)求 ;
(Ⅱ)求数列 的前 1 000 项和.
【答案】(Ⅰ) , , ;(Ⅱ)1893.
【解析】
试题分析:(Ⅰ)先用等差数列的求和公式求公差 ,从而求得通项 ,再根据已知条件
表示不超过的最大整数,求 ;(Ⅱ)对分类讨论,再用分段函数表示 ,再求数
列 的前 1 000 项和.
试题解析:(Ⅰ)设 的公差为 ,据已知有 ,解得
所以 的通项公式为
(Ⅱ)因为
所以数列 的前 项和为
考点:等差数列的的性质,前项和公式,对数的运算.
【名师点睛】解答新颖性的数学题,一是通过转化,化“新”为“旧”;二是通过深入分
析,多方联想,以“旧”攻“新”;三是创造性地运用数学思想方法,以“新”制“新”,
应特别关注创新题型的切入点和生长点.
于是,Bm=Am-dm>2-1=1,Bm-1=min{am,Bm}≥2.
故 dm-1=Am-1-Bm-1≤2-2=0,与 dm-1=1 矛盾.
所以对于任意 n≥1,有 an≤2,即非负整数列{an}的各项只能为 1 或 2.
1 22 n n na a a+ += +
na
2
nS An Bn= +
nS { }na 1 7=1 28.a S =,
[ ]= lgn nb a [ ]x [ ] [ ]0.9 =0 lg99 =1,
1 11 101b b b, ,
{ }nb
1 0b = 11 1b = 101 2b =
d na [ ]x
1 11 101b b b, , nb
{ }nb
{ }na d 7 21 28d+ = 1.d =
{ }na .na n=
1 11 101[lg1] 0, [lg11] 1, [lg101] 2.b b b= = = = = =
0, 1 10,
1, 10 100,
2, 100 1000,
3, 1000.
n
n
nb n
n
≤ <
≤ <= ≤ <
=
{ }nb 1000 1 90 2 900 3 1 1893.× + × + × =
因为对任意 n≥1,an≤2=a1,
所以 An=2.
故 Bn=An-dn=2-1=1.
因此对于任意正整数 n,存在 m 满足 m>n,且 am=1,即数列{an}有无穷多项为 1.
考点定位:本题考查新定义信息题,考查学生对新定义的理解能力和使用能力。
则 ,同理求出 ,通过第一步的计算应用新定义,加深对定
义的认识进入第二步就容易一些了,第二步证明充要条件、第三步的证明就是在第
一步的基础上的深化研究,毕竟是一个新的信息题,在一个全新的环境下进行思维,
需要在原有的知识储备,还需要严密的逻辑思维和分析问题与解决问题的能力,有
得分的机会,但得满分较难.
7. 【2016 高考山东理数】(本小题满分 12 分)
已知数列 的前 n 项和 Sn=3n2+8n, 是等差数列,且
(Ⅰ)求数列 的通项公式;
(Ⅱ)令 求数列 的前 n 项和 Tn.
【答案】(Ⅰ) ;(Ⅱ) .
【解析】
由 ,即 ,可解得 ,
1 1 1d A B= − 1= 2 3 4, ,d d d
{ }na { }nb 1.n n na b b += +
{ }nb
1( 1) .( 2)
n
n
n n
n
ac b
++= + { }nc
13 += nbn
223 +⋅= n
n nT
+=
+=
322
211
bba
bba
+=
+=
db
db
3217
211
1
1 3,41 == db
所以 .
(Ⅱ)由(Ⅰ)知 ,
又 ,
得 ,
,
两式作差,得
所以
考点:1.等差数列的通项公式;2.等差数列、等比数列的求和;3.“错位相减法”.
8.【2015 高考广东,理 21】数列 满足 ,
(1) 求 的值;
(2) 求数列 前项和 ;
(3) 令 , ,证明:数列 的前项和
满足 .
【答案】(1) ;(2) ;(3)见解析.
【解析】(1)依题 ,
13 += nbn
1
1(6 6) 3( 1) 2(3 3)
n
n
n n
nc nn
+
++= = + ⋅+
nn ccccT +⋅⋅⋅+++= 321
2 3 4 13 [2 2 3 2 4 2 ( 1) 2 ]n
nT n += × × + × + × +⋅⋅⋅+ + ×
3 4 5 22 3 [2 2 3 2 4 2 ( 1) 2 ]n
nT n += × × + × + × +⋅⋅⋅+ + ×
2 3 4 1 23 [2 2 2 2 2 ( 1) 2 ]n n
nT n+ +− = × × + + +⋅⋅⋅+ − + ×
2
2
4(2 1)3 [4 ( 1) 2 ]2 1
3 2
n
n
n
n
n
+
+
−= × + − + ×−
= − ⋅
223 +⋅= n
n nT
{ }na ( )*
1 2 1
22 4 2n n
na a na n N−
++ + = − ∈
3a
{ }na nT
1 1b a= ( )1 1 1 11 22 3
n
n n
Tb a nn n
− = + + + +⋅⋅⋅+ ≥
{ }nb nS
nSn ln22 +<
1
4
112 2
n− −
( ) ( )3 1 2 3 1 2 3 1 2 1
3 2 2 2 33 2 3 2 4 42 2 4a a a a a a − −
+ + = + + − + = − − − =
∴ ;
( 2 ) 依 题 当 时 ,
,
∴ ,又 也适合此式,
∴ ,
∴ 数列 是首项为,公比为 的等比数列,故 ;
( 3 ) 依 题 由 知 , ,
,
∴
,
记 ,则 ,
∴ 在 上是增函数,又 即 ,
又 且 时, ,
∴ 即 ,
∴ , , … , , 即 有
3
1
4a =
1n >
( ) ( )1 2 1 2 1 1 2 1
2 12 2 1 4 42 2 2n n n n n n
n n nna a a na a a n a − − − −
+ + = + + − + + − = − − − =
11
2
n
na
− = 1 0
1 24 12a
+= − =
11
2
n
na
− =
{ }na 1
2
1
11 12 21 21 2
n
n
nT
−
− = = − −
1 2 1 1 11 2
n
n n
a a ab an n
−+ + + = + + + +
1 1b a= 1
2 2
112 2
ab a = + +
1 2
3 3
1 113 2 3
a ab a
+ = + + +
( )1 2 1 2
1 1 1 11 12 2n n n nS b b b a a a Tn n
= + + + = + + + + + + = + + +
1
1 1 1 1 11 2 2 12 2 2nn n−
= + + + − < × + + +
( ) ( )1ln 1 1f x x xx
= + − > ( ) 2 2
1 1 1' 0xf x x x x
−= − = >
( )f x ( )1,+∞ ( )1 0f = ( ) 0f x >
2k ≥ *k N∈ 11
k
k
>−
1ln 1 01 1
1
k kf kk k
k
= + − > − −
−
1ln 1
k
k k
>−
1 2ln2 1
< 1 3ln3 2
< 1 ln 1
n
n n
< −
,
∴ ,即 .
【考点定位】前项和关系求项值及通项公式,等比数列前项和,不等式放缩.
( )结合不等( )放缩方法或用数学归纳法证明
.
9.【2016 高考江苏卷】(本小题满分 16 分)
记 .对数列 和 的子集 T,若 ,定义 ;若
, 定 义 . 例 如 : 时 ,
.现设 是公比为 3 的等比数列,且当 时,
.
(1)求数列 的通项公式;
(2)对任意正整数 ,若 ,求证: ;
(3)设 ,求证: .
【答案】(1) (2)详见解析(3)详见解析
【解析】
1 1 1 2 3ln ln ln ln2 3 1 2 1
n nn n
+ + < + + + =−
1 1 12 1 2 2ln2 3 nn
× + + + + < + 2 2lnnS n< +
( ) ( )1ln 1 1f x x xx
= + − > 1ln 1
k
k k
>−
1 1 11 1 ln2 3 nn
+ + + + < +
{ }1,2, 100U = … , { }( )*
na n N∈ U T = ∅ 0TS =
{ }1 2, , kT t t t= … , 1 2
+ kT t t tS a a a= + +… { }= 1,3,66T
1 3 66+TS a a a= + { }( )*
na n N∈ { }= 2,4T
=30TS
{ }na
( )1 100k k≤ ≤ { }1,2, kT ⊆ … , 1T kS a +<
, , C DC U D U S S⊆ ⊆ ≥ 2C C D DS S S+ ≥
13n
na −=
试题解析:(1)由已知得 .
于是当 时, .
又 ,故 ,即 .
所以数列 的通项公式为 .
(2)因为 , ,
所以 .
因此, .
(3)下面分三种情况证明.
①若 是 的子集,则 .
②若 是 的子集,则 .
③若 不是 的子集,且 不是 的子集.
令 , 则 , , .
于是 , ,进而由 ,得 .
设是 中的最大数,为 中的最大数,则 .
由(2)知, ,于是 ,所以 ,即 .
又 ,故 ,
从而 ,
1 *
1 3 ,n
na a n N−= • ∈
{2,4}T = 2 4 1 1 13 27 30rS a a a a a= + = + =
30rS = 130 30a = 1 1a =
{ }na 1 *3 ,n
na n N−= ∈
{1,2, , }T k⊆
1 *3 0,n
na n N−= > ∈
1
1 2
11 3 3 (3 1) 32
k k k
r kS a a a −≤ + + + = + + + = − <
1r kS a +<
D C 2C C D C D D D DS S S S S S S+ = + ≥ + =
C D 2 2C C D C C C DS S S S S S+ = + = ≥
D C C D
UE C C D= UF D C C= E φ≠ F φ≠ E F φ=
C E C DS S S= +
D F C DS S S= +
C DS S≥ E FS S≥
E F 1, 1,k l k l≥ ≥ ≠
1E kS a +< 1
13 3l k
l F E ka S S a−
+= ≤ ≤ < = 1l k− < l k≤
k l≠ 1l k≤ −
1
1 2
1 13 11 3 3 2 2 2
l
l k E
F l
a SS a a a − − −−≤ + + + = + + + = = ≤
故 ,所以 ,
即 .
综合①②③得, .
考点:等比数列的通项公式、求和
10.【2015 江苏高考,20】(本小题满分 16 分)
设 是各项为正数且公差为 d 的等差数列
(1)证明: 依次成等比数列;
(2)是否存在 ,使得 依次成等比数列,并说明理由;
(3)是否存在 及正整数 ,使得 依次成等比数列,并说明理由.
【答案】(1)详见解析(2)不存在(3)不存在
【解析】
试题分析(1)根据等比数列定义只需验证每一项与前一项的比值都为同一个不为零的常数即可
(2)本题列式简单,变形较难,首先令 将二元问题转化为一元,再分别求解两个高次
方程,利用消最高次的方法得到方程: ,无解,所以不存在(3)同(2)先令
将二元问题转化为一元,为降次,所以两边取对数,消去 n,k 得到关于 t 的一元方程
,从而将方程的解转化为研究
函数 零点情况,这个函数
需要利用二次求导才可确定其在 上无零点
试题解析:(1)证明:因为 ( ,,)是同一个常数,
所以 , , , 依次构成等比数列.
2 1E FS S≥ + 2( ) 1C C D D C DS S S S− ≥ − +
2 1C C D DS S S+ ≥ +
2C C D DS S S+ ≥
1 2 3 4, , ,a a a a ( 0)d ≠
31 2 42 ,2 ,2 ,2aa a a
1,a d 2 3 4
1 2 3 4, , ,a a a a
1,a d ,n k knknknn aaaa 3
4
2
321 ,,, +++
1
dt a
=
27 +4 3 0t t + =
1
dt a
=
4ln(1 3 )ln(1 ) ln(1 3 )ln(1 2 ) 3ln(1 2 )ln(1 ) 0t t t t t t+ + − + + − + + =
( ) 4ln(1 3 )ln(1 ) ln(1 3 )ln(1 2 ) 3ln(1 2 )ln(1 )g t t t t t t t= + + − + + − + +
(0, )+∞
1
12 2 22
n
n n
n
a
a a d
a
+
+ −= = 1n =
12a 22a 32a 42a
化简得 (),且 .将 代入()式,
,则 .
显然 不是上面方程得解,矛盾,所以假设不成立,
因此不存在 , ,使得 , , , 依次构成等比数列.
(3)假设存在 , 及正整数,,使得 , , , 依次构成等比数列,
则 ,且 .
分别在两个等式的两边同除以 及 ,并令 ( , ),
则 ,且 .
将上述两个等式两边取对数,得 ,
且 .
化简得 ,
且 .
再将这两式相除,化简得
( ).
令 ,
则 .
令 ,
3 22 2 0t t+ − = 2 1t t= + 2 1t t= +
( ) ( ) 21 2 1 2 3 1 3 4 1 0t t t t t t t t+ + + − = + = + + = + = 1
4t = −
1
4t = −
1a d 1a 2
2a 3
3a 4
4a
1a d 1
na 2
n ka + 2
3
n ka + 3
4
n ka +
( ) ( ) ( )2 2
1 1 12 n k n kna a d a d+ ++ = + ( ) ( ) ( ) ( )3 2 2
1 1 13 2n k n k n ka d a d a d+ + ++ + = +
( )2
1
n ka + ( )2 2
1
n ka +
1
dt a
= 1
3t > − 0t ≠
( ) ( ) ( )2 21 2 1n k n kt t+ ++ = + ( ) ( ) ( ) ( )3 2 21 1 3 1 2n k n k n kt t t+ + ++ + = +
( ) ( ) ( ) ( )2 ln 1 2 2 ln 1n k t n k t+ + = + +
( ) ( ) ( ) ( ) ( ) ( )ln 1 3 ln 1 3 2 2 ln 1 2n k t n k t n k t+ + + + + = + +
( ) ( ) ( ) ( )2 ln 1 2 ln 1 2ln 1 ln 1 2k t t n t t+ − + = + − +
( ) ( ) ( ) ( )3 ln 1 3 ln 1 3ln 1 ln 1 3k t t n t t+ − + = + − +
( ) ( ) ( ) ( ) ( ) ( )ln 1 3 ln 1 2 3ln 1 2 ln 1 4ln 1 3 ln 1t t t t t t+ + + + + = + +
∗∗
( ) ( ) ( ) ( ) ( ) ( ) ( )4ln 1 3 ln 1 ln 1 3 ln 1 2 3ln 1 2 ln 1g t t t t t t t= + + − + + − + +
( ) ( ) ( ) ( ) ( ) ( ) ( )
( )( )( )
2 2 22 1 3 ln 1 3 3 1 2 ln 1 2 3 1 ln 1
1 1 2 1 3
t t t t t t
g t t t t
+ + − + + + + + ′ = + + +
( ) ( ) ( ) ( ) ( ) ( ) ( )2 2 21 3 ln 1 3 3 1 2 ln 1 2 3 1 ln 1t t t t t t tϕ = + + − + + + + +
则 .
令 ,则 .
令 ,则 .
由 , ,
【考点定位】等差、等比数列的定义及性质,函数与方程
【名师点晴】解决等差数列与等比数列的综合问题,关键是理清两个数列的关系.如果同一数
列中部分项成等差数列,部分项成等比数列,要把成等差数列或等比数列的项抽出来单独研究;
如果两个数列通过运算综合在一起,要从分析运算入手,把两个数列分割开,弄清两个数列各
自的特征,再进行求解.
11. 【2015 高考山东,理 18】设数列 的前 n 项和为 .已知 .
(I)求 的通项公式;
(II)若数列 满足 ,求 的前 n 项和 .
【答案】(I) ; (II) .
【解析】
(I)因为
所以, ,故
当 时,
此时, 即
所以,
(II)因为 ,所以
( ) ( ) ( ) ( ) ( ) ( ) ( )6 1 3 ln 1 3 2 1 2 ln 1 2 1 ln 1t t t t t t tϕ′ = + + − + + + + +
( ) ( )1 t tϕ ϕ′= ( ) ( ) ( ) ( )1 6 3ln 1 3 4ln 1 2 ln 1t t t tϕ′ = + − + + +
( ) ( )2 1t tϕ ϕ′= ( ) ( )( )( )2
12 01 1 2 1 3t t t t
ϕ′ = >+ + +
( ) ( ) ( ) ( )1 20 0 0 0 0g ϕ ϕ ϕ= = = = ( )2 0tϕ′ >
{ }na nS 2 3 3n
nS = +
{ }na
{ }nb 3logn n na b a= { }nb nT
1
3, 1,
3 , 1,n n
na
n−
== >
13 6 3
12 4 3n n
nT
+= + ×
2 3 3n
nS = +
12 3 3a = + 1 3,a =
1n > 1
12 3 3,n
nS −
− = +
1
12 2 2 3 3 ,n n
n n na S S −
−= − = − 13 ,n
na −=
1
3, 1,
3 , 1,n n
na
n−
== >
3logn n na b a= 1
1
3b =
当 时,
所以
当 时,
所以
两式相减,得
经检验, 时也适合,
综上可得:
【考点定位】1、数列前项和 与通项 的关系;2、特殊数列的求和问题.
【名师点睛】本题考查了数列的基本概念与运算,意在考查学生的逻辑思维能力与运算求解能
力,思维的严密性和运算的准确性,在利用 与通项 的关系求 的过程中,一定要注意
的情况,错位相减不法虽然思路成熟但也对学生的运算能力提出了较高的要求.
12. 【2016 高考天津理数】已知 是各项均为正数的等差数列,公差为 ,对任意的
是 和 的等差中项.
(Ⅰ)设 ,求证: 是等差数列;
(Ⅱ)设
,求证:
【答案】(Ⅰ)详见解析(Ⅱ)详见解析
【解析】
1n > ( )1 1 1
33 log 3 1 3n n n
nb n− − −= = − ⋅
1 1
1
3T b= =
1n >
( )( )1 2 1
1 2 3
1 1 3 2 3 1 33
n
n nT b b b b n− − −= + + + + = + × + × + + −
( )( )0 1 23 1 1 3 2 3 1 3 n
nT n− −= + × + × + + −
1n =
13 6 3
12 4 3n n
nT
+= + ×
nS na
nS na na
1n =
{ }na d
,bnn N∈ ∗ na 1na +
2 2 *
1 ,n n nc b b n N+= − ∈ { }nc
( )2
2 *
1
1
, 1 ,
n n
n n
k
a d T b n N
=
= = − ∈∑ 2
1
1 1 .2
n
k kT d=
<∑
试题解析:(I)证明:由题意得 ,有 ,
因此 ,所以 是等差数列.
(II)证明:
所以 .
考点:等差数列、等比中项、分组求和、裂项相消求和
【名师点睛】分组转化法求和的常见类型
(1)若 an=bn±cn,且{bn},{cn}为等差或等比数列,可采用分组求和法求{an}的前 n
项和.
(2)通项公式为 an=Error!的数列,其中数列{bn},{cn}是等比数列或等差数列,可采用分组求和
法求和.
13. 【2016 高考新课标 3 理数】已知数列 的前 n 项和 ,其中 .
(I)证明 是等比数列,并求其通项公式;
(II)若 ,求 .
【答案】(Ⅰ) ;(Ⅱ) .
【解析】
2
1n n nb a a += 2 2
1 1 2 1 12n n n n n n n nc b b a a a a da+ + + + += − = − =
( ) 2
1 2 12 2n n n nc c d a a d+ + +− = − = { }nc
( ) ( ) ( )2 2 2 2 2 2
1 2 3 4 2 1 2n n nT b b b b b b−= − + + − + + − +
( ) ( ) ( )2 2 2
2 4 22 2 2 12
n
n
n a ad a a a d d n n
+= + + + = ⋅ = +
( )2 2 2 2
1 1 1
1 1 1 1 1 1 1 1 112 1 2 1 2 1 2
n n n
k k kkT d k k d k k d n d= = =
= = − = ⋅ − < + + + ∑ ∑ ∑
{ }na 1n nS aλ= + 0λ ≠
{ }na
5
31
32S = λ
1)1(1
1 −
−−= n
na λ
λ
λ 1λ = −
由 , 得 ,即 .
由 , 得 ,所以 .
因此 是首项为 ,公比为 的等比数列,于是 .
(Ⅱ)由(Ⅰ)得 ,由 得 ,即 ,
解得 .
考点:1、数列通项 与前项和为 关系;2、等比数列的定义与通项及前项和为 .
【方法总结】等比数列的证明通常有两种方法:(1)定义法,即证明 (常数);(2)
中项法,即证明 .根据数列的递推关系求通项常常要将递推关系变形,转化为等
比数列或等差数列来求解.
14. 【2014 新课标,理 17】(本小题满分 12 分)
已知数列 满足 =1, .
(Ⅰ)证明 是等比数列,并求 的通项公式;
(Ⅱ)证明: .
【解析】:(Ⅰ)证明:由 得 ,所以 ,所以
是等比数列,首项为 ,公比为 3,所以 ,解得
.
(Ⅱ)由(Ⅰ)知: ,所以 ,
因 为 当 时 , , 所 以 , 于 是
= ,
nn aS λ+=1 11 1 ++ += nn aS λ nnn aaa λλ −= ++ 11 nn aa λλ =−+ )1(1
01 ≠a 0≠λ 0≠na 1
1
−=+
λ
λ
n
n
a
a
}{ na λ−1
1
1−λ
λ 1)1(1
1 −
−−= n
na λ
λ
λ
n
nS )1(1 −−= λ
λ
32
31
5 =S 32
31)1(1 5 =−− λ
λ =−
5)1(λ
λ
32
1
1λ = −
na nS nS
1n
n
a qa
+ =
2
1 2n n na a a+ +=
{ }na 1a 1 3 1n na a+ = +
{ }1
2na + { }na
1 2
31 1 1
2na a a
+ + <… +
1 3 1n na a+ = + 1
1 13( )2 2n na a+ + = + 1
1
2 31
2
n
n
a
a
+ +
=
+
1
2na + 1
1 3
2 2a + = 1
2na + = 13 32
n−⋅ na =
3 1
2
n −
na = 3 1
2
n − 1 2
3 1n
na
= −
1n ≥ 13 1 2 3n n−− ≥ ⋅
1
1 1
3 1 2 3n n−≤− ⋅ 1
1
a
+
2
1
a
+
1
na
1
1 11 3 3n−≤ + + +
3 1(1 )2 3n
− 3
2
<
所以 .
【考点定位】1.等比数列;2.等比数列的前 n 项和公式;3.放缩法.
15.【2015 高考四川,理 16】设数列 的前 项和 ,且 成等差
数列.
(1)求数列 的通项公式;
(2)记数列 的前 n 项和 ,求得 成立的 n 的最小值.
【答案】(1) ;(2)10.
【解析】(1)由已知 ,有 ,
即 .
从而 .
又因为 成等差数列,即 .
所以 ,解得 .
所以,数列 是首项为 2,公比为 2 的等比数列.
故 .
(2)由(1)得 .
所以 .
由 ,得 ,即 .
因为 ,
所以 .
于是,使 成立的 n 的最小值为 10.
【考点定位】本题考查等差数列与等比数列的概念、等比数列通项公式与前 n 项和公式等基础
知识,考查运算求解能力.
1
1
a
+
2
1
a
+
1
na
3
2
<
{ }na n 12n nS a a= − 1 2 3, 1,a a a+
{ }na
1{ }
na nT 1| 1| 1000nT − <
2n
na =
12n nS a a= − 1 12 2 ( 1)n n n n na S S a a n− −= − = − >
12 ( 1)n na a n−= >
2 1 3 12 , 4a a a a= =
1 2 3, 1,a a a+ 1 3 22( 1)a a a+ = +
1 1 14 2(2 1)a a a+ = + 1 2a =
{ }na
2n
na =
1 1
2n
na
=
2 3
1 1[1 ( ) ]1 1 1 1 12 2 112 2 2 2 21 2
n
n n nT
−
= + + + + = = −
−
1| 1| 1000nT − < 1 1|1 1|2 1000n
− − < 2 1000n >
9 102 512 1000 1024 2= < < =
10n ≥
1| 1| 1000nT − <
16. 【2016 高考浙江理数】设数列 满足 , .
(I)证明: , ;
(II)若 , ,证明: , .
【答案】(I)证明见解析;(II)证明见解析.
【解析】
试题分析:(I)先利用三角形不等式得 ,变形为 ,再用累加
法可得 ,进而可证 ;(II)由(I)可得 ,
进而可得 ,再利用 的任意性可证 .
试题解析:(I)由 得 ,故
, ,
所以
,
因此
.
(II)任取 ,由(I)知,对于任意 ,
{ }na 1 12
n
n
aa +− ≤ n ∗∈Ν
( )1
12 2n
na a−≥ − n ∗∈Ν
3
2
n
na ≤ n ∗∈Ν 2na ≤ n ∗∈Ν
1
1 12n na a +− ≤ 1
1
1
2 2 2
n n
n n n
a a +
+− ≤
1 12 2
n
n
a a− < ( )1
12 2n
na a−≥ − 1
1
2 2 2
n m
n m n
a a
−− <
32 24
m
n
na < + ⋅ m 2na ≤
1 12
n
n
aa +− ≤ 1
1 12n na a +− ≤
1
1
1
2 2 2
n n
n n n
a a +
+− ≤ n ∗∈Ν
1 1 2 2 3 1
1 1 2 2 3 12 2 2 2 2 2 2 2
n n n
n n n
a a a a a a a a−
−
− = − + − +⋅⋅⋅+ −
1 2 1
1 1 1
2 2 2n−≤ + +⋅⋅⋅+
1<
( )1
12 2n
na a−≥ −
n ∗∈Ν m n>
,
故
从而对于任意 ,均有
.
由 的任意性得 . ①
否则,存在 ,有 ,取正整数 且 ,则
,
与①式矛盾.
综上,对于任意 ,均有 .
考点:1、数列;2、累加法;3、证明不等式.
【 思 路 点 睛 】( I ) 先 利 用 三 角 形 不 等 式 及 变 形 得 , 再 用 累 加 法 可 得
, 进 而 可 证 ; ( II ) 由 ( I ) 的 结 论 及 已 知 条 件 可 得
1 1 2 1
1 1 2 12 2 2 2 2 2 2 2
n m n n n n m m
n m n n n n m m
a a a a a a a a+ + + −
+ + + −
− = − + − +⋅⋅⋅+ −
1 1
1 1 1
2 2 2n n m+ −≤ + +⋅⋅⋅+
1
1
2n−<
m n>
32 24
m
n
na < + ⋅
m 2na ≤
0n ∗∈Ν
0
2na > 0
00 3
4
2
log 2
n
n
a
m
−
> 0 0m n>
0
0 3 0
40 0
0
2
log
23 32 2 24 4
n
n
a
m
m n
na
−
⋅ < ⋅ = −
n ∗∈Ν 2na ≤
1
1
1
2 2 2
n n
n n n
a a +
+− ≤
1 12 2
n
n
a a− < ( )1
12 2n
na a−≥ −
,再利用 的任意性可证 .
17.【2015 高考新课标 1,理 17】 为数列{ }的前项和.已知 >0, = .
(Ⅰ)求{ }的通项公式;
(Ⅱ)设 ,求数列{ }的前项和.
【答案】(Ⅰ) (Ⅱ)
【解析】
试题解析:(Ⅰ)当 时, ,因为 ,所以 =3,
当 时 , = = , 即
,因为 ,所以 =2,
所以数列{ }是首项为 3,公差为 2 的等差数列,
所以 = ;
(Ⅱ)由(Ⅰ)知, = ,
所以数列{ }前 n 项和为 = =
.
【考点定位】数列前 n 项和与第 n 项的关系;等差数列定义与通项公式;拆项消去法
【名师点睛】已知数列前 n 项和与第 n 项关系,求数列通项公式,常用
将所给条件化为关于前 n 项和的递推关系或是关于第 n 项的递推关系,若满足等比数列或等差
数列定义,用等比数列或等差数列通项公式求出数列的通项公式,否则适当变形构造等比或等
数列求通项公式.
18. 【2014 课标Ⅰ,理 17】
已知数列 的前项和为 , , , ,其中 为常数,
32 24
m
n
na < + ⋅ m 2na ≤
nS na na 2
n na a+ 4 3nS +
na
1
1
n
n n
b a a +
= nb
2 1n + 1 1
6 4 6n
− +
1n = 2
1 1 1 12 4 3 4 +3a a S a+ = + = 0na > 1a
2n ≥ 2 2
1 1n n n na a a a− −+ − − 14 3 4 3n nS S −+ − − 4 na
1 1 1( )( ) 2( )n n n n n na a a a a a− − −+ − = + 0na > 1n na a −−
na
na 2 1n +
nb 1 1 1 1( )(2 1)(2 3) 2 2 1 2 3n n n n
= −+ + + +
nb 1 2 nb b b+ + +
1 1 1 1 1 1 1[( ) ( ) ( )]2 3 5 5 7 2 1 2 3n n
− + − + + −+ +
1 1
6 4 6n
− +
1
1
, 1
, 2n
n n
S na S S n−
== − ≥
{ }na nS 1 1a = 0na ≠ 1 1n n na a Sλ+ = − λ
(I)证明: ;
(II)是否存在 ,使得 为等差数列?并说明理由.
【答案】(I)详见解析;(II)存在, .
【解析】
因此存在 ,使得 为等差数列.
【考点定位】1、递推公式;2、数列的通项公式;3、等差数列.
【名师点睛】本题考查了递推公式、等差数列的通项公式及其前 n 项和公式和概念、等差数列
的充要条件等基础知识与基本技能方法, 考查了考生运用数列的有关知识解题的能力和观察、
分析、归纳、猜想及用数学归纳法证明的能力,同时考查了考生的推理能力和计算能力、分类
讨论的思想方法.
19. 【2016 年高考北京理数】(本小题 13 分)
设数列 A: , ,… ( ).如果对小于 ( )的每个正整数都有 < ,
则称是数列 A 的一个“G 时刻”.记“ 是数列 A 的所有“G 时刻”组成的集合.
(1)对数列 A:-2,2,-1,1,3,写出 的所有元素;
(2)证明:若数列 A 中存在 使得 > ,则 ;
(3)证明:若数列 A 满足 - ≤1(n=2,3, …,N),则 的元素个数不小于 - .
【答案】(1) 的元素为和;(2)详见解析;(3)详见解析.
【解析】
试题分析:(1)关键是理解 G 时刻的定义,根据定义即可写出 的所有元素;
(2)要证 ,即证 中含有一元素即可;
2n na a λ+ − =
λ { }na
4λ =
4λ = { }na
1a 2a Na N ≥ 2 n N≤ ≤ ka na
)(AG
)(AG
na na 1a ∅≠)(AG
na 1na − )(AG Na 1a
( )G A
)(AG
∅≠)(AG )(AG
(3)当 时,结论成立.只要证明当 时仍然成立即可.
试题解析:(1) 的元素为和.
(3)当 时,结论成立.
以下设 .
由(Ⅱ)知 .
设 ,记 .
则 .
对 ,记 .
如果 ,取 ,则对任何 .
从而 且 .
又因为 是 中的最大元素,所以 .
从而对任意 , ,特别地, .
对 .
因此 .
所以 .
考点:数列、对新定义的理解.
1aaN ≤ 1aaN >
)(AG
1aaN ≤
1aaN >
∅≠)(AG
{ } pp nnnnnnAG <⋅⋅⋅<<⋅⋅⋅= 2121 ,,,,)( 10 =n
pnnnn aaaa <⋅⋅⋅<<<
210
pi ,,1,0 ⋅⋅⋅= { }
inkii aaNknNkG >≤<∈= ∗ ,
∅≠iG ii Gm min=
ii mnki aaamk <≤<≤ ,1
)(AGmi ∈ 1+= ii nm
pn )(AG ∅=pG
nknp ≤≤
pnk aa ≤
pnN aa ≤
ii nn aapi ≤−⋅⋅⋅= −+ 11
,1,,1,0
1)( 11 1111
+≤−+= −− ++++ iiiii nnnnn aaaaa
paaaaaa iip n
p
i
nnN ≤−=−≤−
−
∑
=
)( 1
1
11
20. 【2015 高考浙江,理 20】已知数列 满足 = 且 = - ( )
(1)证明:1 ( );
(2)设数列 的前项和为 ,证明 ( ).
【答案】(1)详见解析;(2)详见解析.
试题分析:(1)首先根据递推公式可得 ,再由递推公式变形可知
,从而得证;(2)由 和 得,
,从而可得 ,即可得证.
试题解析:(1)由题意得, ,即 , ,由
得 ,由 得,
,即 ;(2)由题意得 ,
∴ ①,由 和 得, ,
∴ ,因此 ②,由①②得
.
【考点定位】数列与不等式结合综合题.
{ }na 1a 1
2 1na + na 2
na n∈ *N
1
2n
n
a
a +
≤ ≤ n∈ *N
{ }2
na nS 1 1
2( 2) 2( 1)
nS
n n n
≤ ≤+ + n∈ *N
1
2na ≤
2
1
1 [1,2]1
n n
n n n n
a a
a a a a+
= = ∈− − 1 1
1 1 = n
n n n
a
a a a+ +
−
1
1 2n
n
a
a +
≤ ≤
1
1 11 2
n na a+
≤ − ≤ *
1
1 1 ( )2( 1) 2na n Nn n+≤ ≤ ∈+ +
2
1 0n n na a a+ − = − ≤ 1n na a+ ≤ 1
2na ≤ 1 1(1 )n n na a a− −= −
1 2 1 1(1 )(1 ) (1 ) 0n n na a a a a− −= − − ⋅⋅⋅ − > 10 2na< ≤
2
1
1 [1,2]1
n n
n n n n
a a
a a a a+
= = ∈− − 1
1 2n
n
a
a +
≤ ≤ 2
1n n na a a += −
1 1n nS a a += −
1 1
1 1 = n
n n n
a
a a a+ +
−
1
1 2n
n
a
a +
≤ ≤
1
1 11 2
n na a+
≤ − ≤
1 1
1 1 2
n
n na a+
≤ − ≤ *
1
1 1 ( )2( 1) 2na n Nn n+≤ ≤ ∈+ +
1 1
2( 2) 2( 1)
nS
n n n
≤ ≤+ +
21. 【2015 高考重庆,理 22】在数列 中,
(1)若 求数列 的通项公式;
(2)若 证明:
【答案】(1) ;(2)证明见解析.
【解析】
试题分析:(1)由于 ,因此把已知等式具体化得 ,显然由于
,则 (否则会得出 ),从而 ,所以 是等比数列,由其通
项 公 式 可 得 结 论 ; ( 2 ) 本 小 题 是 数 列 与 不 等 式 的 综 合 性 问 题 , 数 列 的 递 推 关 系 是
可变形为 ,
由 于 , 因 此 , 于 是 可 得 , 即 有
, 又
, 于 是 有
{ }na ( )2
1 1 13, 0n n n na a a a a n Nλ µ+ + += + + = ∈
0, 2,λ µ= = − { }na
( )0 0
0
1 , 2 , 1,k N kk
λ µ+= ∈ ≥ = −
0 1
0 0
1 12 23 1 2 1kak k++ < < ++ +
13 2n
na −= ⋅
0, 2λ µ= = − 2
1 2n n na a a+ =
1 3a = 0na ≠ 1 0a = 1 2n na a+ = { }na
2
1 1
0
1 0,n n n na a a ak+ ++ - = 2
1
0
1
n n na a ak+
+ =
( )Nn +∈
0 0k >
0
11
n
n
a
a k
<
+ 1n na a+ <
1 2 13 0n na a a a += > > > > > >
2
2 2 2
0 0
1
0 0 0
0 0
1 1
1 1 1
1 1 1
n
n
n n
n
n n
aa k ka a k k k aa ak k
+
- +
= = = - + × ++ +
( ) ( )0 0 01 1 2 1 1k k ka a a a a a+ += + - + + -
0
1 0
0 0 0 1 0 2 0
1 1 1 1 1
1 1 1k
a k k k k a k a k a
= − ⋅ + ⋅ + + + + + +
,这里应用了累加求和的思想方法,由这个结论可知 ,因此
,这样结论得证,本题不等式的证
明应用了放缩法.(1)由 ,有
(2)由 ,数列 的递推关系式变为
变形为 .
由上式及 ,归纳可得
因为 ,所以对
求和得
0 0 0 0
1 1 1 12 3 1 3 1 3 1k k k k
> + ⋅ + + + + + +
0
12 3 1k
= + + 2( *)na n N> ∈
0 1ka + =
0
1 0
0 0 0 1 0 2 0
1 1 1 1 1
1 1 1k
a k k k k a k a k a
= − ⋅ + ⋅ + + + + + +
0 0 0 0
1 1 1 12 2 1 2 1 2 1k k k k
< + ⋅ + + + + + +
0
12 2 1k
= + +
0 2λ µ= = −, 2
1 2 ,(n N )n n na a a+ += ∈
0
1 1k
λ µ= = −, { }na
2
1 1
0
1 0,n n n na a a ak+ ++ - = 2
1
0
1
n n na a ak+
+ =
( )Nn +∈
1 3a =
1 2 13 0n na a a a += > > > > > >
2
2 2 2
0 0
1
0 0 0
0 0
1 1
1 1 1
1 1 1
n
n
n n
n
n n
aa k ka a k k k aa ak k
+
- +
= = = - + × ++ +
01,2n k=
( ) ( )0 0 01 1 2 1 1k k ka a a a a a+ += + - + + -
0
1 0
0 0 0 1 0 2 0
0 0 0 0 0
1 1 1 1 1
1 1 1
1 1 1 1 12 23 1 3 1 3 1 3 1
k
a k k k k a k a k a
k k k k k
= − ⋅ + ⋅ + + + + + +
> + ⋅ + + + = + + + + +
另一方面,由上已证的不等式知 得
综上:
【考点定位】等比数列的通项公式,数列的递推公式,不等式的证明,放缩法.,考查探究能力
和推理论证能力,考查创新意识.
22. 【2015 高考安徽,理 18】设 , 是曲线 在点 处的切线与 x
轴交点的横坐标.
(Ⅰ)求数列 的通项公式;
(Ⅱ)记 ,证明 .
【答案】(Ⅰ) ;(Ⅱ) .
【解析】
试题分析:(Ⅰ)对题中所给曲线的解析式进行求导,得出曲线 在点 处的
切线斜率为 .从而可以写出切线方程为 .令 .解得切线与轴
交点的横坐标 .
0 01 2 1 2k ka a a a +> > > > >
0
0
1 1 0
0 0 0 1 0 2 0
1 1 1 1 1
1 1 1k
k
a a k k k k a k a k a+
= − ⋅ + ⋅ + + + + + +
0 0 0 0 0
1 1 1 1 12 22 1 2 1 2 1 2 1k k k k k
< + ⋅ + + + = + + + + +
0 1
0 0
1 12 23 1 2 1kak k++ < < ++ +
*n N∈ nx 2 2 1ny x += + (1 2),
{ }nx
2 2 2
1 3 2 1n nT x x x −=
1
4nT n
≥
1n
nx n
= +
1
4nT n
≥
2 2 1ny x += + (1 2),
2 2n + 2 (2 2)( 1)y n x− = + − 0y =
11 1 1n
nx n n
= − =+ +
(Ⅱ)证:由题设和(Ⅰ)中的计算结果知
.
当 时, .
当 时,因为 ,
所以 .
综上可得对任意的 ,均有 .
【考点定位】1.曲线的切线方程;2.数列的通项公式;3.放缩法证明不等式.
【名师点睛】数列是特殊的函数,不等式是深刻认识函数与数列的重要工具,三者的综合是近
几年高考命题的新热点,且数列的重心已经偏移到不等式的证明与求解中,而不再是以前
的递推求通项,此类问题在 2010 年、2012 年、2013 年安徽高考解答题中都曾考过.对于数
列问题中求和类(或求积类)不等式证明,如果是通过放缩的方法进行证明的,一般有两
种类型:一种是能够直接求和(或求积),再放缩;一种是不能直接求和(或求积),需要
放缩后才能求和(或求积),求和(或求积)后再进行放缩.在后一种类型中,一定要注意
放缩的尺度,二是要注意从哪一项开始放缩.
23. 【2016 年高考四川理数】(本小题满分 12 分)
已知数列{ }的首项为 1, 为数列 的前 n 项和, ,其中 q>0,
.
2 2 2 2 2 2
1 3 2 1
1 3 2 1( ) ( ) ( )2 4 2n n
nT x x x n−
−= =
1n = 1
1
4T =
2n ≥
2 2 2
2 2
2 1 2 2 2
2 1 (2 1) (2 1) 1 4 4 1( )2 (2 ) (2 ) (2 )n
n n n n n nx n n n n n−
− − − − − −= = > = =
21 1 2 1 1( )2 2 3 4n
nT n n
−> × × × × =
*n N∈ 1
4nT n
≥
na nS { }na 1 1n nS qS+ = +
*n N∈
(Ⅰ)若 成等差数列,求 的通项公式;
( Ⅱ ) 设 双 曲 线 的 离 心 率 为 , 且 , 证 明 :
.
【答案】(Ⅰ) ;(Ⅱ)详见解析.
【解析】
试题分析:(Ⅰ)已知 的递推式 ,一般是写出当 时, ,
两式相减,利用 ,得出数列 的递推式,从而证明 为等比数列,利用
等比数列的通项公式得到结论;(Ⅱ)先利用双曲线的离心率定义得到 的表达式,再由
解出的值,要证明 2016 年高考四川理数不等式,一般想法是求出和 ,
但 数 列 的 和 不 可 求 , 因 此 我 们 利 用 放 缩 法 得 , 从 而 有
,右边的和是等比数列的和,可求,此和即为要证不等式的右边.
最后利用等比数列的求和公式计算证明.
试题解析:(Ⅰ)由已知, 两式相减得到 .
又由 得到 ,故 对所有 都成立.
所以,数列 是首项为 1,公比为 q 的等比数列.
从而 .
由 成等比数列,可得 ,即 ,则 ,
由已知, ,故 .
所以 .
(Ⅱ)由(Ⅰ)可知, .
所以双曲线 的离心率 .
由 解得 .
2 3 22 , , 2a a a + { }na
2
2
2 1
n
yx a
− = ne 2
5
3e =
1 2 1
4 3
3
n n
n ne e e −
−+ +⋅⋅⋅+ >
1= n
na q -
nS 1 1n nS qS+ = + 2n ≥ 1 1n nS qS −= +
1n n na S S −= − { }na { }na
ne
2
5
3e = 1 2 ne e e+ + +
{ }ne 1n
ne q −> 1 2 ne e e+ + +
11 nq q −> + + +
1 2 11, 1,n n n nS qS S qS+ + += + = + 2 1, 1n na qa n+ += ³
2 1 1S qS= + 2 1a qa= 1n na qa+ = 1n ³
{ }na
1= n
na q -
2 3 22 +2a a a, , 3 22 =3 2a a + 22 =3 2,q q + (2 1)( 2) 0q+ q - =
0q > =2q
1 *2 ( )n
na n-= Î N
1n
na q -=
2
2
2 1
n
yx a- = 2 2( 1)1 1 n
n ne a q -= + = +
2 51 3q q= + =
4
3q =
因为 ,所以 .
于是 ,
故 .
考点:数列的通项公式、双曲线的离心率、等比数列的求和公式.
24. 【 2015 高 考 天 津 , 理 18 】( 本 小 题 满 分 13 分 ) 已 知 数 列 满 足
,且
成等差数列.
(I)求的值和 的通项公式;
(II)设 ,求数列 的前项和.
【答案】(I) ; (II) .
【解析】(I) 由已知,有 ,即 ,
所以 ,又因为 ,故 ,由 ,得 ,
当 时, ,
当 时, ,
所以 的通项公式为
(II) 由(I)得 ,设数列 的前项和为 ,则
2( 1) 2( 1)1+ k kq q- -> 2( 1) 1 *1+ k kq q k- -> Î N( )
1
1 2
11+ 1
n
n
n
qe e e q q q
- -+ +×××+ > +×××+ = -
1 2 3 1
4 3
3
n n
ne e e -
-+ +×××+ >
{ }na
2 1 2( ) *, 1, 2n na qa q q n N a a+ = ≠ ∈ = =为实数,且 1,
2 3 3 4 4 5, ,a a a a a a+ + +
{ }na
*2 2
2 1
log ,n
n
n
ab n Na −
= ∈ { }nb
1
2
2
2 ,
2 , .
n
n n
na
n
−
=
为奇数,
为偶数
1
24 2n n
nS −
+= −
( ) ( ) ( ) ( )3 4 2 3 4 5 3 4a a a a a a a a+ - + = + - + 4 2 5 3a a a a− = −
2 3( 1) ( 1)a q a q− = − 1q ≠ 3 2 2a a= = 3 1a a q= 2q =
2 1( *)n k n N= − ∈
1
1 2
2 1 2 2
n
k
n ka a
−
−
−= = =
2 ( *)n k n N= ∈ 2
2 2 2
n
k
n ka a= = =
{ }na
1
2
2
2 ,
2 , .
n
n n
na
n
−
=
为奇数,
为偶数
2 2
1
2 1
log
2
n
n n
n
a nb a −
−
= = { }nb nS
,
两式相减得
,
整理得
所以数列 的前项和为 .
【考点定位】等差数列定义、等比数列及前项和公式、错位相减法求和.
25. 【2015 高考湖北,理 18】设等差数列 的公差为 d,前项和为 ,等比数列 的公
比为.已知 , , , .
(Ⅰ)求数列 , 的通项公式;
(Ⅱ)当 时,记 ,求数列 的前项和 .
【答案】(Ⅰ) 或 ;(Ⅱ) .
【解析】(Ⅰ)由题意有, 即
解得 或 故 或
0 1 2 1
1 1 1 11 2 32 2 2 2n nS n −= × + × + × + + ×
1 2 3
1 1 1 1 11 2 32 2 2 2 2n nS n= × + × + × + + ×
2 3 1
111 1 1 1 1 221 212 2 2 2 2 2 2 2 21 2
n
n n n n n n
n n nS −
−
= + + + + + − = − = − −
−
1
24 2n n
nS −
+= −
{ }nb 1
24 , *2n
n n N−
+− ∈
{ }na nS { }nb
1 1b a= 2 2b = q d= 10 100S =
{ }na { }nb
1d > n
n
n
ac b
= { }nc nT
1
2 1,
2 .
n
n
n
a n
b −
= − = 1
1 (2 79),9
29 ( ) .9
n
n
n
a n
b −
= +
= ⋅
1
2 36 2n
n
−
+−
1
1
10 45 100,
2,
a d
a d
+ =
=
1
1
2 9 20,
2,
a d
a d
+ =
=
1 1,
2,
a
d
=
=
1 9,
2.9
a
d
= =
1
2 1,
2 .
n
n
n
a n
b −
= − = 1
1 (2 79),9
29 ( ) .9
n
n
n
a n
b −
= +
= ⋅
【考点定位】等差数列、等比数列通项公式,错位相减法求数列的前项和.
【名师点睛】错位相减法适合于一个由等差数列 及一个等比数列 对应项
之积组成的数列.考生在解决这类问题时,都知道利用错位相减法求解,也都能写
出此题的解题过程,但由于步骤繁琐、计算量大导致了漏项或添项以及符号出错
等.两边乘公比后,对应项的幂指数会发生变化,应将相同幂指数的项对齐,这样
有一个式子前面空出一项,另外一个式子后面就会多了一项,两项相减,除第一项
和最后一项外,剩下的 项是一个等比数列.
}{ na }{ nb
1−n