春季高考高职单招数学模拟试题 11页

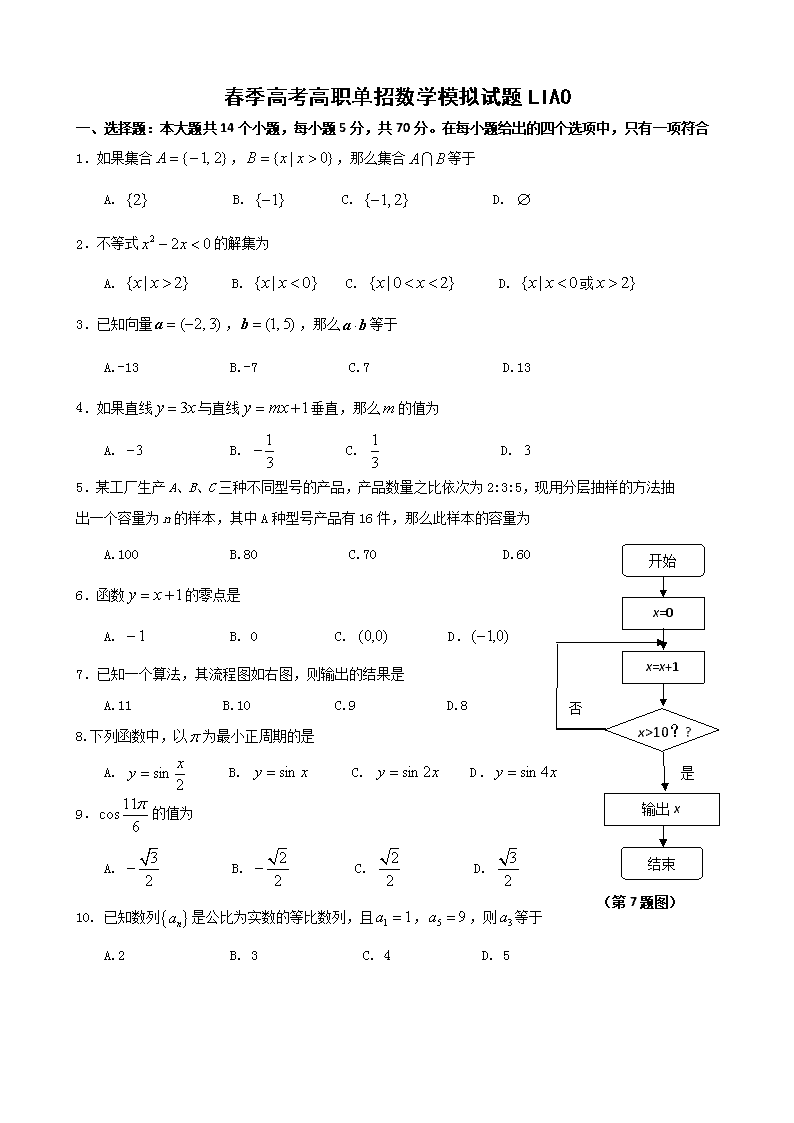
春季高考高职单招数学模拟试题LIAO 一、选择题：本大题共14个小题，每小题5分，共70分。在每小题给出的四个选项中，只有一项符合 ‎1．如果集合，，那么集合等于 A. B. C. D. ‎ ‎2．不等式的解集为 A. B. C. D. 或 ‎3．已知向量，，那么等于 A.-13 B.‎-7 C.7 D.13‎ ‎4．如果直线与直线垂直，那么的值为 A. B. C. D. ‎ ‎5．某工厂生产A、B、C三种不同型号的产品，产品数量之比依次为2:3:5，现用分层抽样的方法抽出一个容量为n的样本，其中A种型号产品有16件，那么此样本的容量为 开始 x=0‎ x=x+1‎ x>10？?‎ 输出x 结束 是 否 ‎（第7题图）‎ A.100 B‎.80 C.70 D.60‎ ‎6．函数的零点是 A. B. ‎0 C. D． ‎ ‎7．已知一个算法，其流程图如右图，则输出的结果是 A.11 B‎.10 C.9 D.8‎ ‎8.下列函数中，以为最小正周期的是 A. B. C. D． ‎ ‎9．的值为 A. B. C. D. ‎ ‎10. 已知数列是公比为实数的等比数列，且，，则等于 A.2 B. ‎3 C. 4 D. 5‎ ‎11．当满足条件 时，目标函数的最大值是 A.1 B‎.2 C.4 D.9‎ ‎12.已知直线l过点，圆C:，则直线l与圆C的位置关系是 A.相交 B. 相切 C.相交或相切 D.相离 ‎13. 已知函数，则下列说法中正确的是 A. 为奇函数，且在上是增函数B. 为奇函数，且在上是减函数 C. 为偶函数，且在上是增函数D. 为偶函数，且在上是减函数 ‎14．已知平面、，直线、，下面的四个命题 ‎①；②；③；④中，‎ 所有正确命题的序号是 A. ①② B. ②③ C. ①④ D. ②④‎ 1、 若集合S=｛小于9的正整数｝，M=｛2,4｝，N=｛3,4,5,7｝，则()()=( )‎ A ｛2,3,4,5,7｝ B ｛1,6,8｝‎ C ｛1,2,3,5,6,7,8｝ D ｛4｝‎ ‎2、不等式＞0的解集是( ).‎ A ｛︱＜＜｝ B ｛︱＞-3｝‎ C ｛︱＞0｝ D ｛︱≠-3｝‎ ‎3、已知，，，那么的大小顺序是( )。‎ A ＜＜ B ＜＜‎ C ＜＜ D ＜＜‎ ‎4、若＜0且＜0，则是( ).‎ A 第一象限的角 B 第二象限的角 C 第三象限的角 D 第四象限的角 ‎5、若、为实数，则的充分必要条件是( ).‎ A = B ︱︱=︱︱‎ C = D ==0‎ ‎8、已知＞0，＜0，＜0，那么直线的图象必经过（ ）。‎ A 第一、二、三象限 B 第一、二、四象限 C 第一、三、四象限 D 第二、三、四象限]‎ ‎9、已知点A(-1,3)，B(-3,-1)，那么线段AB的垂直平分线方程是（ ）。‎ A B ‎ C D ‎ ‎10、甲、乙两人各进行一次射击，如果甲击中目标的概率为0.6，乙击中目标的概率为0.7，那么至少一人击中目标的概率是（ ）。‎ A 0.86 B 0.42‎ C 0.88 D 0.90‎ 二、 填空题：本大题共4个小题，每小题5分，共20分。请把答案写在答题卡相应的位置上。‎ ‎（第17题图）‎ ‎15. 计算的结果为 ． ‎ ‎16. 复数 在复平面内对应的点在第 象限． ‎ ‎17.如图 ，在边长为2的正方形内有一内切圆，现从正方形内取一点P，则点P在圆内的概率为__ _．‎ ‎1、不等式︱2-3︱＜2的解集是 。‎ ‎2、函数的定义域是 。‎ ‎19.（本小题满分8分）‎ 已知等差数列满足：，的前项和为.求及； ‎ 已知≥，求的取值范围。‎ ‎20.（本小题满分8分）一批食品，每袋的标准重量是50，为了了解这批食品的实际重量情况，从中随机抽取10袋食品，称出各袋的重量（单位：），并得到其茎叶图（如图）．‎ ‎（1）求这10袋食品重量的众数，并估计这批食品实际重量的平均数；‎ ‎（2）若某袋食品的实际重量小于或等于47，则视为不合格产品，试估计这批食品重量的合格率．‎ ‎4 5 6 6 9‎ ‎5 0 0 0 1 1 2‎ ‎ ‎ ‎ ‎ ‎（第20题图）‎ ‎21.（本小题满分10分）如图，在正方体中，是棱的中点．‎ ‎（第21题图）‎ ‎（Ⅰ）证明：∥平面； （Ⅱ）证明：.‎ ‎22. （本小题满分10分）在平面直角坐标系中，角的顶点与原点重合，始边与轴的正半轴重合，终边分别与单位圆交于两点，两点的纵坐标分别为．‎ ‎（Ⅰ）求的值； （Ⅱ）求的面积．‎ ‎23.（本小题满分12分）设半径长为5的圆C满足条件：‎ ‎①截y轴所得弦长为6；②圆心在第一象限．并且到直线的距离为．‎ ‎（Ⅰ）求这个圆的方程；‎ ‎（Ⅱ）求经过P（-1，0）与圆C相切的直线方程．‎ ‎24. （本小题满分12分）已知函数，，．‎ ‎ （Ⅰ）若，试判断并证明函数的单调性；‎ ‎ （Ⅱ）当时，求函数的最大值的表达式．‎ 海沧中学2015届春季高考高职单招数学模拟试题 参考答案 一．选择题（每题5分，共70分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ ‎13‎ ‎14‎ 选项 A C D B B D A C D B C C B A 二．填空题（每题5分，共20分）‎ ‎15. 2 16. 第二象限 17． 18. 或 三．解答题 ‎19. （本小题满分8分）‎ 解：设等差数列的首项为，公差为，因为 所以 ………………………………2分 解得 ………………………………4分 从而 ………………………………6分 ‎ ………………………………8分 ‎20.（本小题满分8分）‎ 解：（1）这10袋食品重量的众数为50（）， …………………………2分 因为这10袋食品重量的平均数为 ‎（）， ‎ 所以可以估计这批食品实际重量的平均数为49（）； ………………………4分 ‎（2）因为这10袋食品中实际重量小于或等于47的有3袋，‎ 所以可以估计这批食品重量的不合格率为， ………………………6分 故可以估计这批食品重量的合格率为． ………………………8分 ‎21．（本小题满分10分）(I)证明：连接AC交BD于O,连接OE,‎ 因为ABCD是正方形，所以O为AC的中点，因为E是棱CC1的中点， ‎ 所以AC1∥OE. ………………………………2分 又因为AC1平面BDE,‎ OE平面BDE,‎ 所以AC1∥平面BDE. ………………………………5分 ‎(II) 证明因为ABCD是正方形，所以AC⊥BD. ‎ 因为CC1⊥平面ABCD,且BD平面ABCD,所以CC1⊥BD. ‎ 又因为CC1∩AC=C,所以BD⊥平面ACC1. ………………………………8分 又因为AC1平面ACC1，‎ 所以AC1⊥BD. ………………………………10分 ‎22．（本小题满分10分）‎ 解：(I)因为在单位圆中，B点的纵坐标为，所以， ‎ 因为，所以， ‎ 所以. ………………………………3分 ‎(II)解：因为在单位圆中，A点的纵坐标为，所以.‎ 因为，所以.‎ 由(I)得，， ………………………………6分 所以=. ………………………8分 又因为|OA|=1，|OB|=1,所以△AOB的面积 ‎. ………………………………10分 ‎23．（本小题满分12分）‎ ‎（1）由题设圆心，半径=5‎ 截轴弦长为6‎ ‎ ……………2分 由到直线的距离为 ‎（2）①设切线方程 由到直线的距离 ……………8分 切线方程： ……………10分 ‎24．（本小题满分12分）‎ ‎(1)判断：若，函数在上是增函数. ……………1分 ‎ 证明：当时，，‎ ‎ 在区间上任意，设，‎ ‎ ‎ ‎ 所以，即在上是增函数. ……………4分 ‎（注：若用导数证明同样给分）‎ ‎ (2)因为，所以……………6分 ‎ ①当时，在上是增函数，在上也是增函数，‎ ‎ 所以当时，取得最大值为； ……………8分 ‎ ②当时，在上是增函数，在上是减函数，在上是 增函数，而，‎ ‎ 当时，，当时，函数取最大值为；‎ ‎ 当时，，当时，函数取最大值为；………11分 综上得， ……………12分