全国统一高考数学试卷文科新课标ⅱ 15页

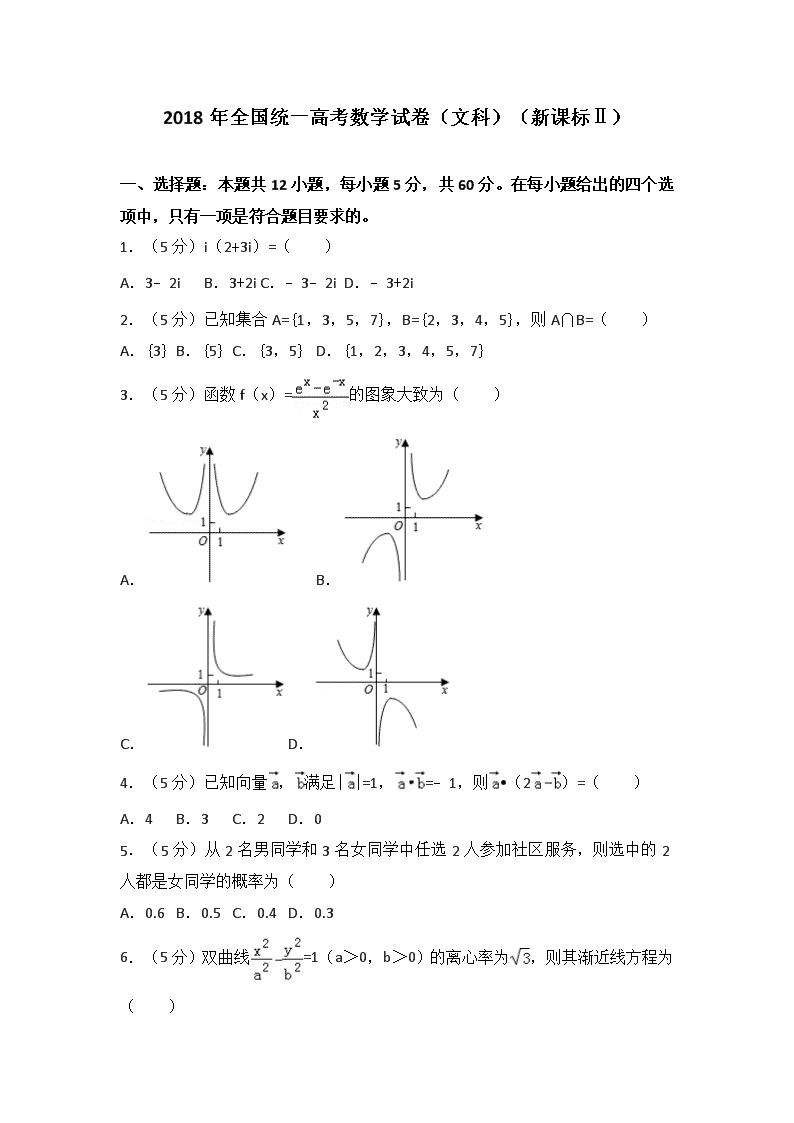
‎2018年全国统一高考数学试卷（文科）（新课标Ⅱ） ‎ ‎　‎ 一、选择题：本题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。‎ ‎1．（5分）i（2+3i）=（　　）‎ A．3﹣2i B．3+2i C．﹣3﹣2i D．﹣3+2i ‎2．（5分）已知集合A={1，3，5，7}，B={2，3，4，5}，则A∩B=（　　）‎ A．{3} B．{5} C．{3，5} D．{1，2，3，4，5，7}‎ ‎3．（5分）函数f（x）=的图象大致为（　　）‎ A． B． ‎ C． D．‎ ‎4．（5分）已知向量，满足||=1，=﹣1，则•（2）=（　　）‎ A．4 B．3 C．2 D．0‎ ‎5．（5分）从2名男同学和3名女同学中任选2人参加社区服务，则选中的2人都是女同学的概率为（　　）‎ A．0.6 B．0.5 C．0.4 D．0.3‎ ‎6．（5分）双曲线=1（a＞0，b＞0）的离心率为，则其渐近线方程为（　　）‎ A．y=±x B．y=±x C．y=±x D．y=±x ‎7．（5分）在△ABC中，cos=，BC=1，AC=5，则AB=（　　）‎ A．4 B． C． D．2‎ ‎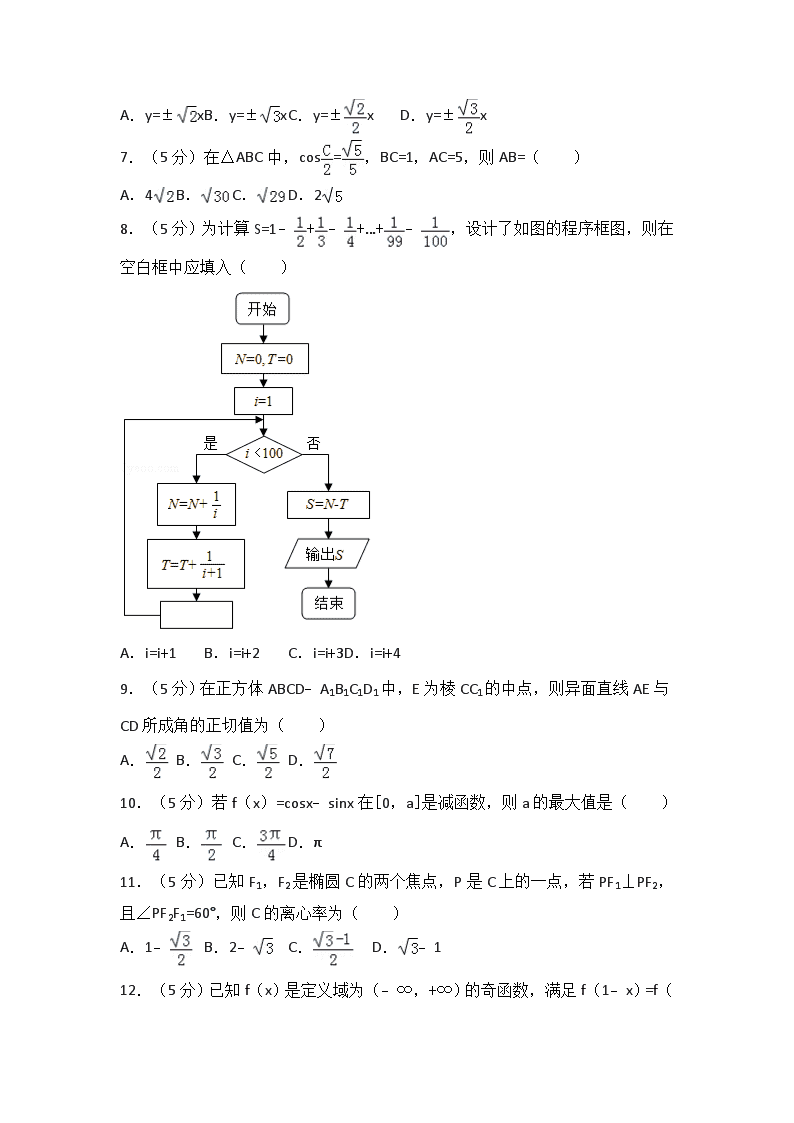8．（5分）为计算S=1﹣+﹣+…+﹣，设计了如图的程序框图，则在空白框中应填入（　　）‎ A．i=i+1 B．i=i+2 C．i=i+3 D．i=i+4‎ ‎9．（5分）在正方体ABCD﹣A1B1C1D1中，E为棱CC1的中点，则异面直线AE与CD所成角的正切值为（　　）‎ A． B． C． D．‎ ‎10．（5分）若f（x）=cosx﹣sinx在[0，a]是减函数，则a的最大值是（　　）‎ A． B． C． D．π ‎11．（5分）已知F1，F2是椭圆C的两个焦点，P是C上的一点，若PF1⊥PF2，且∠PF2F1=60°，则C的离心率为（　　）‎ A．1﹣ B．2﹣ C． D．﹣1‎ ‎12．（5分）已知f（x）是定义域为（﹣∞，+∞‎ ‎）的奇函数，满足f（1﹣x）=f（1+x），若f（1）=2，则f（1）+f（2）+f（3）+…+f（50）=（　　）‎ A．﹣50 B．0 C．2 D．50‎ ‎　‎ 二、填空题：本题共4小题，每小题5分，共20分。‎ ‎13．（5分）曲线y=2lnx在点（1，0）处的切线方程为　 　．‎ ‎14．（5分）若x，y满足约束条件，则z=x+y的最大值为　 　．‎ ‎15．（5分）已知tan（α﹣）=，则tanα=　 　．‎ ‎16．（5分）已知圆锥的顶点为S，母线SA，SB互相垂直，SA与圆锥底面所成角为30°．若△SAB的面积为8，则该圆锥的体积为　 　．‎ ‎　‎ 三、解答题：共70分。解答应写出文字说明、证明过程或演算步骤。第17～21题为必考题，每个试题考生都必须作答。第22、23题为选考题，考生根据要求作答。（一）必考题：共60分。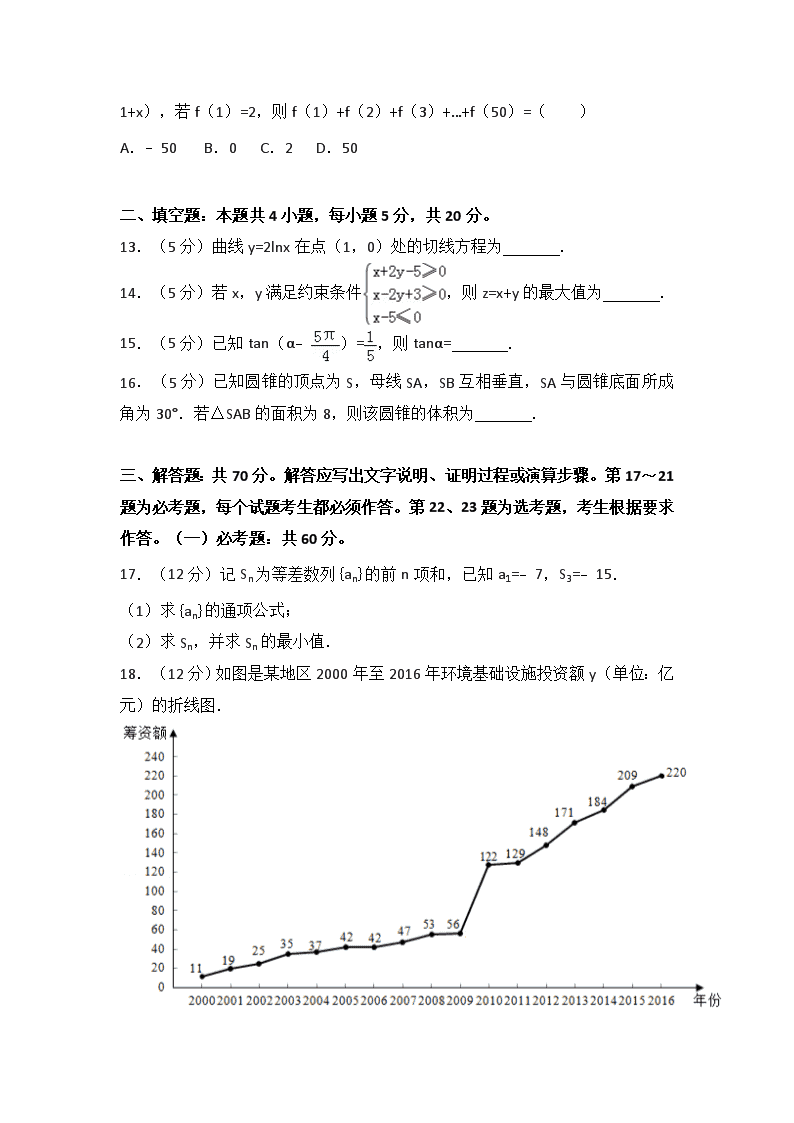‎ ‎17．（12分）记Sn为等差数列{an}的前n项和，已知a1=﹣7，S3=﹣15．‎ ‎（1）求{an}的通项公式；‎ ‎（2）求Sn，并求Sn的最小值．‎ ‎18．（12分）如图是某地区2000年至2016年环境基础设施投资额y（单位：亿元）的折线图．‎ 为了预测该地区2018年的环境基础设施投资额，建立了y与时间变量t的两个线性回归模型．根据2000年至2016年的数据（时间变量t的值依次为1，2，…，17）建立模型①：=﹣30.4+13.5t；根据2010年至2016年的数据（时间变量t的值依次为1，2，…，7）建立模型②：=99+17.5t．‎ ‎（1）分别利用这两个模型，求该地区2018年的环境基础设施投资额的预测值；‎ ‎（2）你认为用哪个模型得到的预测值更可靠？并说明理由．‎ ‎19．（12分）如图，在三棱锥P﹣ABC中，AB=BC=2，PA=PB=PC=AC=4，O为AC的中点．‎ ‎（1）证明：PO⊥平面ABC；‎ ‎（2）若点M在棱BC上，且MC=2MB，求点C到平面POM的距离．‎ ‎20．（12分）设抛物线C：y2=4x的焦点为F，过F且斜率为k（k＞0）的直线l与C交于A，B两点，|AB|=8．‎ ‎（1）求l的方程；‎ ‎（2）求过点A，B且与C的准线相切的圆的方程．‎ ‎21．（12分）已知函数f（x）=x3﹣a（x2+x+1）．‎ ‎（1）若a=3，求f（x）的单调区间；‎ ‎（2）证明：f（x）只有一个零点．‎ ‎　‎ ‎（二）选考题：共10分。请考生在第22、23题中任选一题作答。如果多做，则按所做的第一题计分。[选修4-4：坐标系与参数方程]（10分）‎ ‎22．（10分）在直角坐标系xOy中，曲线C的参数方程为 ‎，（θ为参数），直线l的参数方程为，（t为参数）．‎ ‎（1）求C和l的直角坐标方程；‎ ‎（2）若曲线C截直线l所得线段的中点坐标为（1，2），求l的斜率．‎ ‎　‎ ‎[选修4-5：不等式选讲]（10分）‎ ‎23．设函数f（x）=5﹣|x+a|﹣|x﹣2|．‎ ‎（1）当a=1时，求不等式f（x）≥0的解集；‎ ‎（2）若f（x）≤1，求a的取值范围．‎ ‎　‎ ‎2018年全国统一高考数学试卷（文科）（新课标Ⅱ）答案 ‎ 一、选择题：本题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。‎ ‎1．【解答】解：i（2+3i）=2i+3i2=﹣3+2i．‎ 故选：D．　‎ ‎2．【解答】解：∵集合A={1，3，5，7}，B={2，3，4，5}，‎ ‎∴A∩B={3，5}．‎ 故选：C．　‎ ‎3．【解答】解：函数f（﹣x）==﹣=﹣f（x），‎ 则函数f（x）为奇函数，图象关于原点对称，排除A，‎ 当x=1时，f（1）=e﹣＞0，排除D．‎ 当x→+∞时，f（x）→+∞，排除C，‎ 故选：B．　‎ ‎4．【解答】解：向量，满足||=1，=﹣1，则•（2）=2﹣=2+1=3，‎ 故选：B．　‎ ‎5．【解答】解：（适合理科生）从2名男同学和3名女同学中任选2人参加社区服务，共有C52=10种，其中全是女生的有C32=3种，‎ 故选中的2人都是女同学的概率P==0.3，‎ ‎（适合文科生），设2名男生为a，b，3名女生为A，B，C，‎ 则任选2人的种数为ab，aA，aB，aC，bA，bB，Bc，AB，AC，BC共10种，其中全是女生为AB，AC，BC共3种，‎ 故选中的2人都是女同学的概率P==0.3，‎ 故选：D．　‎ ‎6．【解答】解：∵双曲线的离心率为e==，‎ 则=====，‎ 即双曲线的渐近线方程为y=±x=±x，‎ 故选：A．　‎ ‎7．【解答】解：在△ABC中，cos=，cosC=2×=﹣，‎ BC=1，AC=5，则AB====4．‎ 故选：A．　‎ ‎8．【解答】解：模拟程序框图的运行过程知，‎ 该程序运行后输出的是 S=N﹣T=（1﹣）+（﹣）+…+（﹣）；‎ 累加步长是2，则在空白处应填入i=i+2．‎ 故选：B．　‎ ‎9．【解答】解：以D为原点，DA为x轴，DC为y轴，DD1为z轴，建立空间直角坐标系，‎ 设正方体ABCD﹣A1B1C1D1棱长为2，‎ 则A（2，0，0），E（0，2，1），D（0，0，0），‎ C（0，2，0），‎ ‎=（﹣2，2，1），=（0，﹣2，0），‎ 设异面直线AE与CD所成角为θ，‎ 则cosθ===，‎ sinθ==，‎ ‎∴tanθ=．‎ ‎∴异面直线AE与CD所成角的正切值为．‎ 故选：C．　‎ ‎10．【解答】解：f（x）=cosx﹣sinx=﹣（sinx﹣cosx）=﹣sin（x﹣），‎ 由﹣+2kπ≤x﹣≤+2kπ，k∈Z，‎ 得﹣+2kπ≤x≤+2kπ，k∈Z，‎ 取k=0，得f（x）的一个减区间为[﹣，]，‎ 由f（x）在[0，a]是减函数，‎ 得a≤．‎ 则a的最大值是．‎ 故选：C．　‎ ‎11．【解答】解：F1，F2是椭圆C的两个焦点，P是C上的一点，若PF1⊥PF2，且∠PF2F1=60°，可得椭圆的焦点坐标F2（c，0），‎ 所以P（c，c）．可得：，可得，可得e4﹣8e2+4=0，e∈（0，1），‎ 解得e=．‎ 故选：D．‎ ‎　‎ ‎12．【解答】解：∵f（x）是奇函数，且f（1﹣x）=f（1+x），‎ ‎∴f（1﹣x）=f（1+x）=﹣f（x﹣1），f（0）=0，‎ 则f（x+2）=﹣f（x），则f（x+4）=﹣f（x+2）=f（x），‎ 即函数f（x）是周期为4的周期函数，‎ ‎∵f（1）=2，‎ ‎∴f（2）=f（0）=0，f（3）=f（1﹣2）=f（﹣1）=﹣f（1）=﹣2，‎ f（4）=f（0）=0，‎ 则f（1）+f（2）+f（3）+f（4）=2+0﹣2+0=0，‎ 则f（1）+f（2）+f（3）+…+f（50）=12[f（1）+f（2）+f（3）+f（4）]+f（49）+f（50）‎ ‎=f（1）+f（2）=2+0=2，‎ 故选：C．　‎ 二、填空题：本题共4小题，每小题5分，共20分。‎ ‎13．【解答】解：∵y=2lnx，‎ ‎∴y′=，‎ 当x=1时，y′=2‎ ‎∴曲线y=2lnx在点（1，0）处的切线方程为y=2x﹣2．‎ 故答案为：y=2x﹣2．　‎ ‎14．【解答】解：由x，y满足约束条件作出可行域如图，‎ 化目标函数z=x+y为y=﹣x+z，‎ 由图可知，当直线y=﹣x+z过A时，z取得最大值，‎ 由，解得A（5，4），‎ 目标函数有最大值，为z=9．‎ 故答案为：9．‎ ‎　‎ ‎15．【解答】解：∵tan（α﹣）=，‎ ‎∴tan（α）=，‎ 则tanα=tan（α+）=====，‎ 故答案为：．‎ ‎16．【解答】解：圆锥的顶点为S，母线SA，SB互相垂直，△SAB的面积为8，可得：，解得SA=4，‎ SA与圆锥底面所成角为30°．可得圆锥的底面半径为：2，圆锥的高为：2，‎ 则该圆锥的体积为：V==8π．‎ 故答案为：8π．　‎ 三、解答题：共70分。解答应写出文字说明、证明过程或演算步骤。第17～21题为必考题，每个试题考生都必须作答。第22、23题为选考题，考生根据要求作答。（一）必考题：共60分。‎ ‎17．【解答】解：（1）∵等差数列{an}中，a1=﹣7，S3=﹣15，‎ ‎∴a1=﹣7，3a1+3d=﹣15，解得a1=﹣7，d=2，‎ ‎∴an=﹣7+2（n﹣1）=2n﹣9；‎ ‎（2）∵a1=﹣7，d=2，an=2n﹣9，‎ ‎∴Sn===n2﹣8n=（n﹣4）2﹣16，‎ ‎∴当n=4时，前n项的和Sn取得最小值为﹣16．　‎ ‎18．【解答】解：（1）根据模型①：=﹣30.4+13.5t，‎ 计算t=19时，=﹣30.4+13.5×19=226.1；‎ 利用这个模型，求出该地区2018年的环境基础设施投资额的预测值是226.1亿元；‎ 根据模型②：=99+17.5t，‎ 计算t=9时，=99+17.5×9=256.5；．‎ 利用这个模型，求该地区2018年的环境基础设施投资额的预测值是256.5亿元；‎ ‎（2）模型②得到的预测值更可靠；‎ 因为从总体数据看，该地区从2000年到2016年的环境基础设施投资额是逐年上升的，‎ 而从2000年到2009年间递增的幅度较小些，‎ 从2010年到2016年间递增的幅度较大些，‎ 所以，利用模型②的预测值更可靠些．　‎ ‎19．【解答】（1）证明：∵AB=BC=2，AC=4，∴AB2+BC2=AC2，即△ABC是直角三角形，‎ 又O为AC的中点，∴OA=OB=OC，‎ ‎∵PA=PB=PC，∴△POA≌△POB≌△POC，∴∠POA=∠POB=∠POC=90°，‎ ‎∴PO⊥AC，PO⊥OB，OB∩AC=0，∴PO⊥平面ABC；‎ ‎（2）解：由（1）得PO⊥平面ABC，PO=，‎ 在△COM中，OM==．‎ S=××=，‎ S△COM==．‎ 设点C到平面POM的距离为d．由VP﹣OMC=VC﹣POM⇒，‎ 解得d=，‎ ‎∴点C到平面POM的距离为．　‎ ‎20．【解答】解：（1）方法一：抛物线C：y2=4x的焦点为F（1，0），当直线的斜率不存在时，|AB|=4，不满足；‎ 设直线AB的方程为：y=k（x﹣1），设A（x1，y1），B（x2，y2），‎ 则，整理得：k2x2﹣2（k2+2）x+k2=0，则x1+x2=，x1x2=1，‎ 由|AB|=x1+x2+p=+2=8，解得：k2=1，则k=1，‎ ‎∴直线l的方程y=x﹣，；‎ 方法二：抛物线C：y2=4x的焦点为F（1，0），设直线AB的倾斜角为θ，由抛物线的弦长公式|AB|===8，解得：sin2θ=，‎ ‎∴θ=，则直线的斜率k=1，‎ ‎∴直线l的方程y=x﹣1；‎ ‎（2）过A，B分别向准线x=﹣1作垂线，垂足分别为A1，B1，设AB的中点为D，过D作DD1⊥准线l，垂足为D，则|DD1|=（|AA1|+|BB1|）‎ 由抛物线的定义可知：|AA1|=|AF|，|BB1|=|BF|，则r=|DD1|=4，‎ 以AB为直径的圆与x=﹣1相切，且该圆的圆心为AB的中点D，‎ 由（1）可知：x1+x2=6，y1+y2=x1+x2﹣2=4，‎ 则D（3，2），‎ 过点A，B且与C的准线相切的圆的方程（x﹣3）2+（y﹣2）2=16．．‎ ‎　‎ ‎21．【解答】解：（1）当a=3时，f（x）=x3﹣a（x2+x+1），‎ 所以f′（x）=x2﹣6x﹣3时，令f′（x）=0解得x=3，‎ 当x∈（﹣∞，3﹣2），x∈（3﹣2，+∞）时，f′（x）＞0，函数是增函数，‎ 当x∈（3﹣2时，f′（x）＜0，函数是单调递减，‎ 综上，f（x）在（﹣∞，3﹣2），（3﹣2，+∞），上是增函数，在（3﹣2上递减．‎ ‎（2）证明：因为x2+x+1=（x+）2+，‎ 所以f（x）=0等价于，‎ 令，‎ 则，所以g（x）在R上是增函数；‎ 取x=max{9a，1}，则有=，‎ 取x=min{9a，﹣1}，则有=，‎ 所以g（x）在（min{9a，﹣1}，max{9a，1}‎ ‎）上有一个零点，由单调性则可知，f（x）只有一个零点．‎ ‎　‎ ‎（二）选考题：共10分。请考生在第22、23题中任选一题作答。如果多做，则按所做的第一题计分。[选修4-4：坐标系与参数方程]（10分）‎ ‎22．【解答】解：（1）曲线C的参数方程为（θ为参数），‎ 转换为直角坐标方程为：．‎ 直线l的参数方程为（t为参数）．‎ 转换为直角坐标方程为：sinαx﹣cosαy+2cosα﹣sinα=0．‎ ‎（2）把直线的参数方程代入椭圆的方程得到：+=1‎ 整理得：（4cos2α+sin2α）t2+（8cosα+4sinα）t﹣8=0，‎ 则：，‎ 由于（1，2）为中点坐标，‎ 所以：，‎ 则：8cosα+4sinα=0，‎ 解得：tanα=﹣2，‎ 即：直线l的斜率为﹣2．　‎ ‎[选修4-5：不等式选讲]（10分）‎ ‎23．【解答】解：（1）当a=1时，f（x）=5﹣|x+1|﹣|x﹣2|=．‎ 当x≤﹣1时，f（x）=2x+4≥0，解得﹣2≤x≤1，‎ 当﹣1＜x＜2时，f（x）=2≥0恒成立，即﹣1＜x＜2，‎ 当x≥2时，f（x）=﹣2x+6≥0，解得2≤x≤3，‎ 综上所述不等式f（x）≥0的解集为[﹣2，3]，‎ ‎（2）∵f（x）≤1，‎ ‎∴5﹣|x+a|﹣|x﹣2|≤1，‎ ‎∴|x+a|+|x﹣2|≤4，‎ ‎∴|x+a|+|x﹣2|=|x+a|+|2﹣x|≥|x+a+2﹣x|=|a+2|，‎ ‎∴|a+2|≤4，‎ 即﹣4≤a+2≤4，‎ 解得﹣6≤a≤2，‎ 故a的取值范围[﹣6，2]．‎ ‎　‎