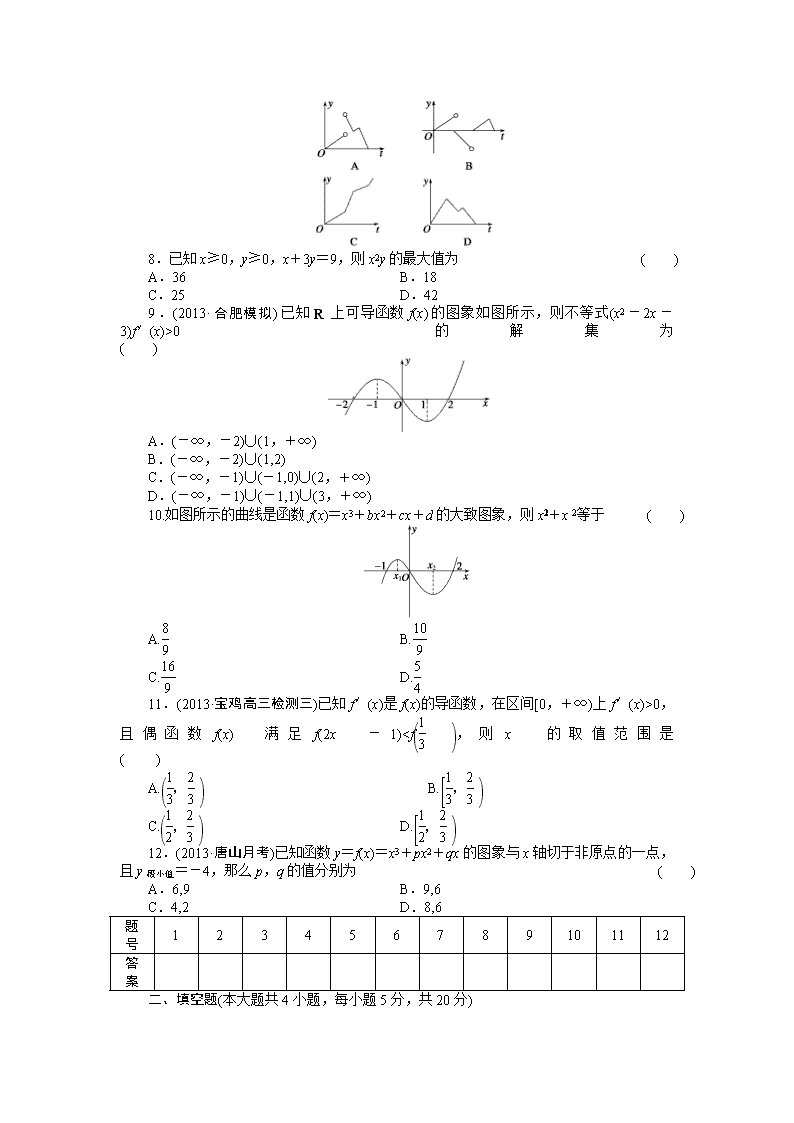2015高考数学第三章（导数及其应用）一轮复习题 9页

第三章　章末检测 ‎(时间：120分钟　满分：150分)‎ 一、选择题(本大题共12小题，每小题5分，共60分)‎ ‎1.(2013·泰安高三二模)如图，函数y＝f(x)的图象在点P(5，f(5))处的切线方程是y＝－x＋8，则f(5)＋f′(5)等于 (　　)‎ A. B．1‎ C．2 D．0‎ ‎2．函数f(x)＝ax3－x在(－∞，＋∞)上是减函数，则 (　　)‎ A．a<1 B．a< C．a<0 D．a≤0‎ ‎3．(2013·洛阳模拟)已知f(x)＝，且f(x－1)的图象的对称中心是(0,3)，则f′(2)的值为 (　　)‎ A．－ B. C．－ D. ‎4．若函数f(x)＝exsin x，则此函数图象在点(4，f(4))处的切线的倾斜角为 (　　)‎ A. B．‎0 ‎ C．钝角 D．锐角 ‎5．(2013·山东)已知某生产厂家的年利润y(单位：万元)与年产量x(单位：万件)的函数关系式为y＝－x3＋81x－234，则使该生产厂家获取最大年利润的年产量为 (　　)‎ A．13万件 B．11万件 C．9万件 D．7万件 ‎6．已知f(x)＝2x3－6x2＋a (a是常数)在[－2,2]上有最大值3，那么在[－2,2]上f(x)的最小值是 (　　)‎ A．－5 B．－11‎ C．－29 D．－37‎ ‎7．(2013·江西) 如图，一个正五角形薄片(其对称轴与水面垂直)匀速地升出水面，记t时刻五角星露出水面部分的图形面积为S(t) (S(0)＝0)，则导函数y＝S′(t)的图象大致(　　)‎ ‎8．已知x≥0，y≥0，x＋3y＝9，则x2y的最大值为 (　　)‎ A．36 B．18‎ C．25 D．42‎ ‎9．(2013·合肥模拟)已知R上可导函数f(x)的图象如图所示，则不等式(x2－2x－3)f′(x)>0的解集为 (　　)‎ A．(－∞，－2)∪(1，＋∞)‎ B．(－∞，－2)∪(1,2)‎ C．(－∞，－1)∪(－1,0)∪(2，＋∞)‎ D．(－∞，－1)∪(－1,1)∪(3，＋∞)‎ ‎10.如图所示的曲线是函数f(x)＝x3＋bx2＋cx＋d的大致图象，则x＋x等于 (　　)‎ A. B. C. D. ‎11．(2013·宝鸡高三检测三)已知f′(x)是f(x)的导函数，在区间[0，＋∞)上f′(x)>0，且偶函数f(x)满足f(2x－1)0的解集是{x|00时，≥3x2在(－∞，＋∞)上恒成立，这样的a不存在；‎ a<0时，≤3x2在(－∞，＋∞)上恒成立，而3x2≥0，‎ ‎∴a<0.综上，a≤0.]‎ ‎3．B　[f(x)＝a＋1－，中心为(－1，a＋1)，由f(x－1)的中心为(0,3)知f(x)的中心为(－1,3)，∴a＝2.‎ ‎∴f(x)＝3－.‎ ‎∴f′(x)＝.∴f′(2)＝.]‎ ‎4．C　[f′(x)＝exsin x＋excos x ‎＝ex(sin x＋cos x)＝exsin，‎ f′(4)＝e4sin<0，‎ 则此函数图象在点(4，f(4))处的切线的倾斜角为钝角．]‎ ‎5．C　[∵y′＝－x2＋81，令y′＝0得x＝9(x＝－9舍去)．‎ 当09时，y′<0，f(x)为减函数．‎ ‎∴当x＝9时，y有最大值．]‎ ‎6．D　[f′(x)＝6x2－12x，若f′(x)>0，‎ 则x<0或x>2，又f(x)在x＝0处连续，‎ ‎∴f(x)的增区间为[－2,0)．‎ 同理f′(x)<0，得减区间(0,2]．‎ ‎∴f(0)＝a最大．‎ ‎∴a＝3，即f(x)＝2x3－6x2＋3.‎ 比较f(－2)，f(2)得f(－2)＝－37为最小值．]‎ ‎7．A　[利用排除法．‎ ‎∵露出水面的图形面积S(t)逐渐增大，‎ ‎∴S′(t)≥0，排除B.‎ 记露出最上端小三角形的时刻为t0.‎ 则S(t)在t＝t0处不可导．排除C、D，故选A.]‎ ‎8．A　[由x＋3y＝9，得y＝3－≥0，∴0≤x≤9.‎ 将y＝3－代入u＝x2y，‎ 得u＝x2＝－＋3x2.‎ u′＝－x2＋6x＝－x(x－6)．‎ 令u′＝0，得x＝6或x＝0.‎ 当00；60，在(－1,1)上f′(x)<0.‎ 由(x2－2x－3)f′(x)>0，‎ 得或 即或，‎ 所以不等式的解集为(－∞，－1)∪(－1,1)∪(3，＋∞)．]‎ ‎10．C　[由图象知f(x)＝x(x＋1)(x－2)‎ ‎＝x3－x2－2x＝x3＋bx2＋cx＋d，‎ ‎∴b＝－1，c＝－2，d＝0.‎ 而x1，x2是函数f(x)的极值点，故x1，x2是f′(x)＝0，‎ 即3x2＋2bx＋c＝0的根，‎ ‎∴x1＋x2＝－，x1x2＝，‎ x＋x＝(x1＋x2)2－2x1x2‎ ‎＝b2－＝.]‎ ‎11．A　[∵x∈[0，＋∞)，f′(x)>0，‎ ‎∴f(x)在[0，＋∞)上单调递增，‎ 又因f(x)是偶函数，∴f(2x－1)0，‎ ‎∴ln x＋1>0，ln x>－1，‎ ‎∴x>.∴递增区间为.‎ ‎14．f(3)0恒成立，‎ 所以f(x)在上为增函数，‎ f(2)＝f(π－2)，f(3)＝f(π－3)，‎ 且0<π－3<1<π－2<，‎ 所以f(π－3)0⇒(2x－x2)ex>0‎ ‎⇒2x－x2>0⇒0或x<－，‎ 由f′(x)>0，得－0，f(x)为增函数；‎ 当x∈时，f′(x)<0，f(x)为减函数；‎ 当x∈(1，＋∞)时，f′(x)>0，f(x)为增函数．…………………………………………(4分)‎ 所以f(x)的递增区间为和(1，＋∞)，‎ f(x)的递减区间为.……………………………………………………………(6分)‎ ‎(2)当x∈[－1,2]时，f(x)7.………………………………………………………………………………(10分)‎ ‎18．解　(1)设切线的斜率为k，‎ 则k＝f′(x)＝2x2－4x＋3＝2(x－1)2＋1，‎ 当x＝1时，kmin＝1.………………………………………………………………………(3分)‎ 又f(1)＝，∴所求切线的方程为y－＝x－1，‎ 即3x－3y＋2＝0.………………………………………………………………………(6分)‎ ‎(2)f′(x)＝2x2－4ax＋3，要使y＝f(x)为单调递增函数，必须满足f′(x)≥0，即对任意的x∈(0，＋∞)，恒有f′(x)≥0，f′(x)＝2x2－4ax＋3≥0，∴a≤＝＋，而＋≥，当且仅当x＝时，等号成立．……………………………………………………………(10分)‎ ‎∴a≤，又∵a∈Z，‎ ‎∴满足条件的最大整数a为1.…………………………………………………………(12分)‎ ‎19．解　(1)f(x)的定义域为(0，＋∞)，f′(x)＝ln x＋1，……………………………(2分)‎ 令f′(x)＝0，得x＝，‎ 当x∈(0，＋∞)时，f′(x)，f(x)的变化的情况如下：‎ x f′(x)‎ ‎－‎ ‎0‎ ‎＋‎ f(x)‎  极小值  ‎…………………………………………………………………………………………(5分)‎ 所以，f(x)在(0，＋∞)上的极小值是f＝－.……………………………………(6分)‎ ‎(2)当x∈，f(x)单调递减且f(x)的取值范围是；‎ 当x∈时，f(x)单调递增且f(x)的取值范围是.………………(8分)‎ 令y＝f(x)，y＝m，两函数图象交点的横坐标是f(x)－m＝0的解，由(1)知当m<－时，原方程无解；‎ 由f(x)的单调区间上函数值的范围知，‎ 当m＝－或m≥0时，原方程有唯一解；‎ 当－0时，①成立，‎ 即成立，解得00，‎ f(x)在区间(64,640)内为增函数，………………………………………………………(10分)‎ 所以f(x)在x＝64处取得最小值，‎ 此时，n＝－1＝－1＝9.‎ 故需新建9个桥墩才能使y最小．……………………………………………………(12分)‎ ‎22．解　(1)因为f′(x)＝ex－1(2x＋x2)＋3ax2＋2bx ‎＝xex－1(x＋2)＋x(3ax＋2b)，‎ 又x＝－2和x＝1为f(x)的极值点，‎ 所以f′(－2)＝f′(1)＝0，‎ 因此…………………………………………………………………(3分)‎ 解方程组得………………………………………………………………(4分)‎ ‎(2)因为a＝－，b＝－1，‎ 所以f′(x)＝x(x＋2)(ex－1－1)，‎ 令f′(x)＝0，解得x1＝－2，x2＝0，x3＝1.……………………………………………(6分)‎ 因为当x∈(－∞，－2)∪(0,1)时，f′(x)<0；‎ 当x∈(－2,0)∪(1，＋∞)时，f′(x)>0.‎ 所以f(x)在(－2,0)和(1，＋∞)上是单调递增的；‎ 在(－∞，－2)和(0,1)上是单调递减的．………………………………………………(8分)‎ ‎(3)由(1)可知f(x)＝x2ex－1－x3－x2，‎ 故f(x)－g(x)＝x2ex－1－x3‎ ‎＝x2(ex－1－x)，‎ 令h(x)＝ex－1－x，则h′(x)＝ex－1－1.…………………………………………………(9分)‎ 令h′(x)＝0，得x＝1，‎ 因为x∈(－∞，1]时，h′(x)≤0，‎ 所以h(x)在x∈(－∞，1]上单调递减．‎ 故x∈(－∞，1]时，h(x)≥h(1)＝0.‎ 因为x∈[1，＋∞)时，h′(x)≥0，‎ 所以h(x)在x∈[1，＋∞)上单调递增．‎ 故x∈[1，＋∞)时，h(x)≥h(1)＝0.……………………………………………………(11分)‎ 所以对任意x∈(－∞，＋∞)，恒有h(x)≥0，‎ 又x2≥0，因此f(x)－g(x)≥0，‎ 故对任意x∈(－∞，＋∞)，‎ 恒有f(x)≥g(x)．…………………………………………………………………………(12分)‎