浙江省2015高考数学模拟卷一 7页

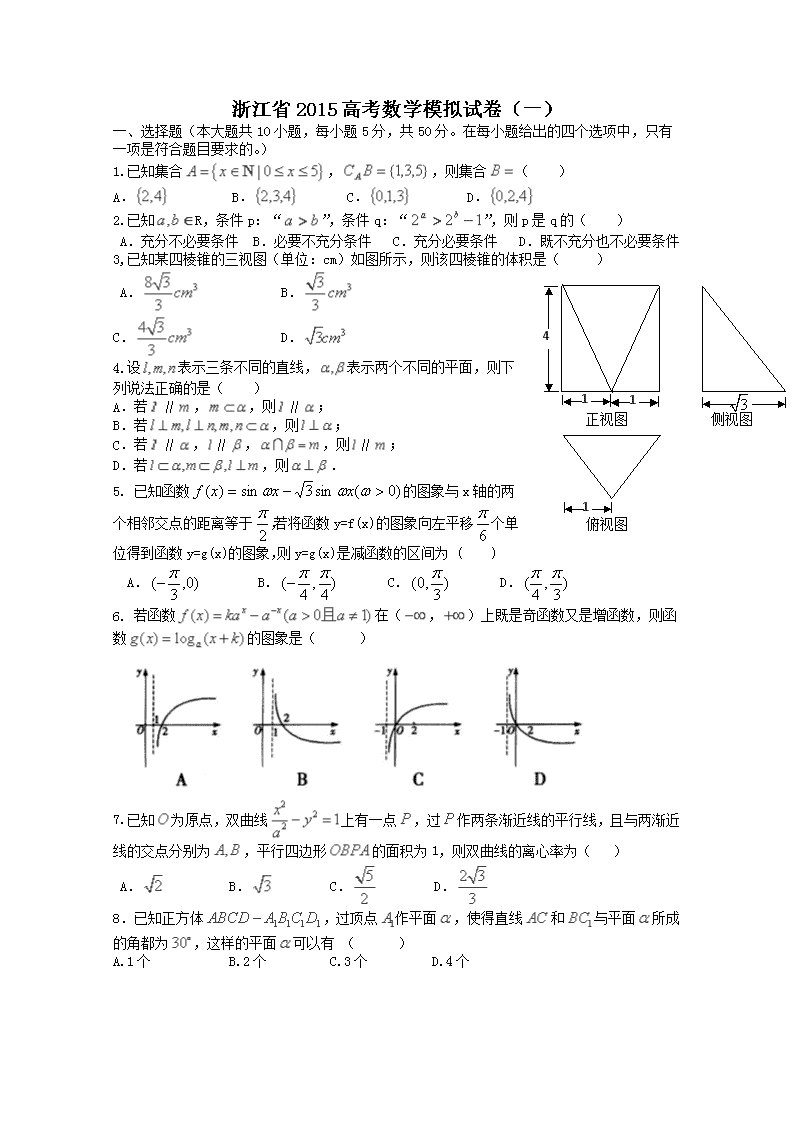
浙江省 2015 高考数学模拟试卷（一） 一、选择题（本大题共 10 小题，每小题 5 分，共 50 分。在每小题给出的四个选项中，只有 一项是符合题目要求的。） 1.已知集合 ， ，则集合 （ ） A． B． C． D． 2.已知 R，条件 p：“ ”，条件 q：“ ”，则 p 是 q 的（ ） A．充分不必要条件 B．必要不充分条件 C．充分必要条件 D．既不充分也不必要条件 3,已知某四棱锥的三视图（单位：cm）如图所示，则该四棱锥的体积是（ ） A． B． C． D． 4.设 表示三条不同的直线， 表示两个不同的平面，则下 列说法正确的是（ ） A．若 ∥ ， ，则 ∥ ； B．若 ，则 ； C．若 ∥ ， ∥ ， ，则 ∥ ； D．若 ，则 ． 5. 已知函数 的图象与 x 轴的两 个相邻交点的距离等于 ，若将函数 y=f(x)的图象向左平移 个单 位得到函数 y=g(x)的图象，则 y=g(x)是减函数的区间为 ( ) A． B． C． D． 6. 若函数 在（ ， ）上既是奇函数又是增函数，则函 数 的图象是（ ） 7.已知 为原点，双曲线 上有一点 ，过 作两条渐近线的平行线，且与两渐近 线的交点分别为 ，平行四边形 的面积为 1，则双曲线的离心率为（ ） A． B． C． D． 8．已知正方体 ，过顶点 作平面 ，使得直线 和 与平面 所成 的角都为 ，这样的平面 可以有 （ ） A.1 个 B.2 个 C.3 个 D.4 个 ∈ba, ba > 122 −> ba { }| 0 5A x x= ∈ ≤ ≤N }5,3,1{=BC A =B { }4,2 { }4,3,2 { }3,1,0 { }4,2,0 38 3 3 cm 33 3 cm 34 3 3 cm 33cm , ,l m n ,α β l m m α⊂ l α , , ,l m l n m n α⊥ ⊥ ⊂ l α⊥ l α l β mα β = l m , ,l m l mα β⊂ ⊂ ⊥ α β⊥ )0(sin3sin)( >−= ωωω xxxf 2 π 6 π )0,3( π− )4,4( ππ− )3,0( π )3,4( ππ ( ) ( 0 1)x xf x ka a a a−= − > ≠且 −∞ +∞ ( ) log ( )ag x x k= + O 2 2 2 1x ya − = P P ,A B OBPA 2 3 5 2 2 3 3 1 1 1 1ABCD A B C D− 1A α AC 1BC α 30 α 4 1 1 3 1 正视图 侧视图 俯视图 9．已知向量 满足 与 的夹角为 ， ，则 的最大值为 （A） （B） （C） （D） 10． 的 边上的高线为 ， ， ，且 ，将 沿 折成 大小为 的二面角 ，若 ，则此时 是（ ） Ａ．锐角三角形 Ｂ．钝角三角形 Ｃ．直角三角形 Ｄ．形状与 ， 的值有关的三角形 二、填空题（本大题共 7 小题，每小题 4 分，共 28 分） 11．式子 的值为__ ___ 12.在 中，角 所对的边分别为 ，若 ， , ,则 角 的大小为 . 13. 设等差数列 的前 项和为 ,若 ,则满足 的正整数 的值为 _______________ 14. 已知实数 满足约束条件 ,若 的最小值为 3，实数 = . 15. 在△ABC 中，B(10，0)，直线 BC 与圆Γ：x2＋(y－5)2＝25 相切，切点为线段 BC 的中 点．若△ABC 的重心恰好为圆Γ的圆心，则点 A 的坐标为 ． 16．若 ，当 时， ，若在区间 内， 有两个零点，则实数 m 的取值范围是 ． 17. 若正实数 满足 ，且不等式 恒成立， 则实数 的取值范围是 ． 三、解答题：本大题共 5 小题，共 72 分．解答应写出文字说明、证明过程或演算步骤． 18．（本小题满分 14 分）在△ABC 中，内角 A,B,C 对边的边长分别是 a,b,c．已知 c=2,C= ． （Ⅰ）若△ABC 的面积等于 ，试判断△ABC 的形状，并说明理由； （Ⅱ）若 sinC+sin(B-A)=2sin2A，求△ABC 的面积． 4 3 27log 3 ABC∆ , ,A B C , ,a b c 2a = 2b = sin cos 2B B+ = A , ,a b c   4, 2 2,a b= =  a b 4 π ( ) ( ) 1c a c b− ⋅ − = −    c a−  12 2 + 2 12 + 2 1 2 + 2 1+ ABC∆ BC AD BD a= CD b= a b< ABC∆ AD θ B AD C− − cos a b θ = ABC∆ a b { }na n nS 6 7 5S S S> > 01 <+nn SS n ,x y 2 0x y y x y x b − ≥  ≥  ≥ − + 2z x y= + b 1( ) 1 ( 1)f x f x + = + [0,1]x∈ ( )f x x= ( ]1,1− ( ) ( )g x f x mx m= − − ,x y 2 4 4x y xy+ + = 2( 2 ) 2 2 34 0x y a a xy+ + + − ≥ a 3 π 3 19．（本小题满分 14 分） 如图，矩形 ABCD 中，AB=2BC=4，E 为边 AB 的中点，将△ADE 沿直线 DE 翻折成△A1DE （1）当平面 A1DE⊥平面 BCD 时，求直线 CD 与平面 A1CE 所成角的正弦值； （2）设 M 为线段 A1C 的中点，求证：在△ADE 翻转过程中，BM 的长度为定值． 20. （本小题满分 14 分）已知等比数列 的公比为 ，且 ． （1）求数列 的通项公式； （2）设该等比数列 的前 项和为 ，正整数 满足 ，求出所有符合条 件的 的值． M E D A B C A1 { }na q ( )0 1q< < 2 5 3 4 9 1,8 8a a a a+ = = { }na { }na n nS ,m n 1 1 2 n n S m S m+ − <− ,m n 21. （本小题满分 15 分）如图，已知直线 l 与抛物线 相切于点 P(2，1)，且与 x 轴 交于点 A，O 为坐标原点，定点 B 的坐标为（2，0）. （I）若动点 M 满足 ，求点 M 的轨迹 C； （II）若过点 B 的直线 l′（斜率不等于零）与（I）中的轨迹 C 交于不同的两点 E、F（E 在 B、F 之间），试求△OBE 与△OBF 面积之比的取值范围. 22. （本题满分 15 分）已知函数 （Ⅰ）若不等式 的解集是{ 或 }，求不等式 的解集； （Ⅱ）若函数 在 上有两个不同的零点 ，求实数 的取值范 围. yx 42 = 0||2 =+⋅ AMBMAB 2 2( ) 1 , ( ) 2, .f x x g x x ax x R= − = + + ∈ ( ) 0g x > | 2x x > 1x < ( ) ( )f x g x≤ ( ) ( ) ( ) 2h x f x g x= + + (0,2) 1 2,x x a 浙江省 2015 高考数学模拟试卷（一） 答案 一、选择题 DAACD,CCCDC 二、填空题 , , 12, , (0，15) 或 (－8，－1), , 三、解答题：本大题共 5 小题，共 49 分．解答应写出文字说明、证明过程或演算步骤． 21 解：（I）由 ， ∴直线 l 的斜率为 ， （用点斜式 ）故 l 的方程为 ，∴点 A 坐标为（1，0），………….2 分 设 ，则 ， 由 得 整理，得 ∴点 M 的轨迹为以原点为中心，焦点在 x 轴上，长轴长为 ，短轴长为 2 的 椭圆 ……… 6 分 （II）如图，由题意知直线 l 的斜率存在且不为零，设 l 方程为 y=k(x－2)(k≠0)① 将①代入 ，整理，得 ， 由△>0 得 0 < − <  − > 5 0 2 11 0 8 4 2 6 2 6 a a a a ora + ≥  + >− < < −  < − > 2 6a < − a 11 2 62 a− < < − 法二： 单调递增，且值域为 ； 先增后减， 作出上述函数图像，可得 ( ) ( ) ( ) [ ) 2 2 2 2 2 2 1 4 5 , 0,11 4 1 4 32 , 1,2 x x xx x x xa x x x x xx x − − − −  = − ∈− − − − = = − − − −  = − + ∈    ( ) 50,1 ,x x ∈ − ( ), 5−∞ − [ ) ( ) 31,2 , 2x k x x x  ∈ = − +   ( ) ( ) ( )max 6 111 5, 2 6, 22 2k k x k k  = − = = − = −    11 2 62 a− < < −