上海市宝山区高考数学一模试卷解析 23页

‎2016年上海市宝山区高考数学一模试卷 ‎　‎ 一．填空题（本大题满分56分）本大题共有14题，只要求直接填写结果，每个空格填对得4分，否则一律得零分．‎ ‎1．方程4x﹣2x﹣6=0的解为　　　　　　．‎ ‎　‎ ‎2．已知：（i是虚数单位 ），则z=　　　　　　．‎ ‎　‎ ‎3．以点（1，2）为圆心，与直线4x+3y﹣35=0相切的圆的方程是　　　　　　．‎ ‎　‎ ‎4．数列所有项的和为　　　　　　．‎ ‎　‎ ‎5．已知矩阵A=，B=，AB=，则x+y=　　　　　　．‎ ‎　‎ ‎6．等腰直角三角形的直角边长为1，则绕斜边旋转一周所形成的几何体的体积为　　　　　　．‎ ‎　‎ ‎7．若（x﹣）9的展开式中x3的系数是﹣84，则a=　　　　　　．‎ ‎　‎ ‎8．抛物线y2=12x的准线与双曲线的两条渐近线所围成的三角形的面积等于　　　　　　．‎ ‎　‎ ‎9．已知ω，t＞0，函数的最小正周期为2π，将f（x）的图象向左平移t个单位，所得图象对应的函数为偶函数，则t的最小值为　　　　　　．‎ ‎　‎ ‎10．两个三口之家，共4个大人，2个小孩，约定星期日乘“奥迪”、“捷达”两辆轿车结伴郊游，每辆车最多只能乘坐4人，其中两个小孩不能独坐一辆车，则不同的乘车方法种数是　　　　　　．‎ ‎　‎ ‎11．向量，满足，，与的夹角为60°，则=　　　　　　．‎ ‎　‎ ‎12．数列，则是该数列的第　　　　　　项．‎ ‎　‎ ‎13．已知直线（1﹣a）x+（a+1）y﹣4（a+1）=0（其中a为实数）过定点P，点Q在函数的图象上，则PQ连线的斜率的取值范围是　　　　　　．‎ ‎　‎ ‎14．如图，已知抛物线y2=x及两点A1（0，y1）和A2（0，y2），其中y1＞y2＞0．过A1，A2分别作y轴的垂线，交抛物线于B1，B2两点，直线B1B2与y轴交于点A3（0，y3），此时就称A1，A2确定了A3．依此类推，可由A2，A3确定A4，…．记An（0，yn），n=1，2，3，…．‎ 给出下列三个结论：‎ ‎①数列{yn}是递减数列；‎ ‎②对∀n∈N*，yn＞0；‎ ‎③若y1=4，y2=3，则．‎ 其中，所有正确结论的序号是　　　　　　．‎ ‎　‎ ‎　‎ 二．选择题（本大题满分20分）本大题共有4题，每题都给出代号为A、B、C、D的四个结论，其中有且只有一个结论是正确的．必须用2B铅笔将正确结论的代号涂黑，选对得5分，不选、选错或者选出的代号超过一个，一律得零分．‎ ‎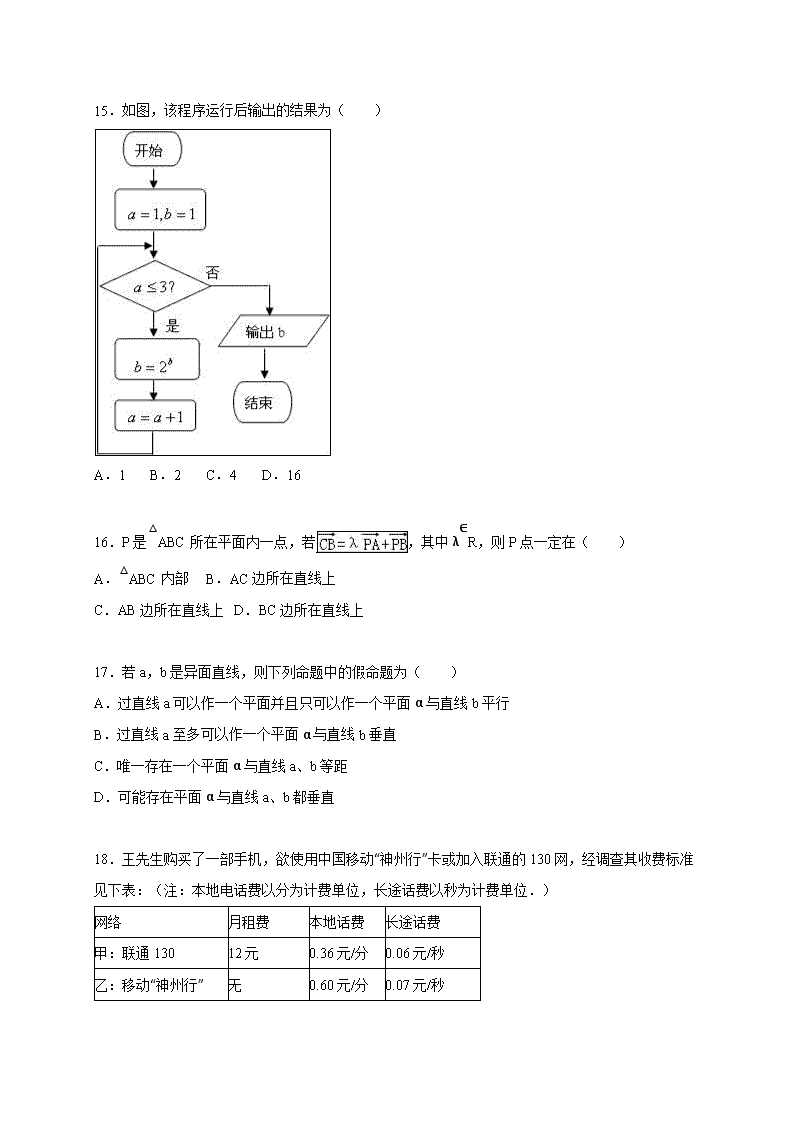15．如图，该程序运行后输出的结果为（　　）‎ A．1 B．2 C．4 D．16‎ ‎　‎ ‎16．P是△ABC所在平面内一点，若，其中λ∈R，则P点一定在（　　）‎ A．△ABC内部 B．AC边所在直线上 C．AB边所在直线上 D．BC边所在直线上 ‎　‎ ‎17．若a，b是异面直线，则下列命题中的假命题为（　　）‎ A．过直线a可以作一个平面并且只可以作一个平面α与直线b平行 B．过直线a至多可以作一个平面α与直线b垂直 C．唯一存在一个平面α与直线a、b等距 D．可能存在平面α与直线a、b都垂直 ‎　‎ ‎18．王先生购买了一部手机，欲使用中国移动“神州行”卡或加入联通的130网，经调查其收费标准见下表：（注：本地电话费以分为计费单位，长途话费以秒为计费单位．）‎ 网络 月租费 本地话费 长途话费 甲：联通130‎ ‎12元 ‎0.36元/分 ‎0.06元/秒 乙：移动“神州行”‎ 无 ‎0.60元/分 ‎0.07元/秒 若王先生每月拨打本地电话的时间是拨打长途电话时间的5倍，若要用联通130应最少打多长时间的长途电话才合算．（　　）‎ A．300秒 B．400秒 C．500秒 D．600秒 ‎　‎ ‎　‎ 三．解答题（本大题满分74分）本大题共有5题，解答下列各题必须写出必要的步骤，答题务必写在黑色矩形边框内．‎ ‎19．在三棱锥P﹣ABC中，已知PA，PB，PC两两垂直，PB=5，PC=6，三棱锥P﹣ABC的体积为20，Q是BC的中点，求异面直线PB，AQ所成角的大小（结果用反三角函数值表示）．‎ ‎　‎ ‎20．设a、b、c分别是△ABC三个内角∠A、∠B、∠C的对边，若向量，且，‎ ‎（1）求tanA•tanB的值；‎ ‎（2）求的最大值．‎ ‎　‎ ‎21．某市2013年发放汽车牌照12万张，其中燃油型汽车牌照10万张，电动型汽车2万张．为了节能减排和控制总量，从2013年开始，每年电动型汽车牌照按50%增长，而燃油型汽车牌照每一年比上一年减少0.5万张，同时规定一旦某年发放的牌照超过15万张，以后每一年发放的电动车的牌照的数量维持在这一年的水平不变．‎ ‎（1）记2013年为第一年，每年发放的燃油型汽车牌照数构成数列{an}，每年发放的电动型汽车牌照数为构成数列{bn}，完成下列表格，并写出这两个数列的通项公式；‎ a1=10‎ a2=9.5‎ a3=　　　　　　‎ a4=　　　　　　‎ ‎…‎ b1=2‎ b2=　　　　　　‎ b3=　　　　　　‎ ‎ b4=　　　　　　‎ ‎…‎ ‎（2）从2013年算起，累计各年发放的牌照数，哪一年开始超过200万张？‎ ‎　‎ ‎22．已知椭圆+y2=1上两个不同的点A，B关于直线对称．‎ ‎（1）若已知，M为椭圆上动点，证明：；‎ ‎（2）求实数m的取值范围；‎ ‎（3）求△AOB面积的最大值（O为坐标原点）．‎ ‎　‎ ‎23．已知函数f（x）=logkx（k为常数，k＞0且k≠1），且数列{f（an）}是首项为4，公差为2的等差数列．‎ ‎（1）求证：数列{an}是等比数列；‎ ‎（2）若bn=an+f（an），当时，求数列{bn}的前n项和Sn的最小值；‎ ‎（3）若cn=anlgan，问是否存在实数k，使得{cn}是递增数列？若存在，求出k的范围；若不存在，说明理由．‎ ‎　‎ ‎　‎ ‎2016年上海市宝山区高考数学一模试卷 参考答案与试题解析 ‎　‎ 一．填空题（本大题满分56分）本大题共有14题，只要求直接填写结果，每个空格填对得4分，否则一律得零分．‎ ‎1．方程4x﹣2x﹣6=0的解为　log23　．‎ ‎【考点】指数式与对数式的互化；二次函数的性质．‎ ‎【专题】计算题．‎ ‎【分析】由4x﹣2x﹣6=0，得（2x）2﹣2x﹣6=0，由此能求出方程4x﹣2x﹣6=0的解．‎ ‎【解答】解：由4x﹣2x﹣6=0，得 ‎（2x）2﹣2x﹣6=0，‎ 解得2x=3，或2x=﹣2（舍去），‎ ‎∴x=log23．‎ 故答案为：log23．‎ ‎【点评】本题考查指数方程的解法，解题时要认真审题，注意指数式和对数式的互化．‎ ‎　‎ ‎2．已知：（i是虚数单位 ），则z=　﹣3﹣4i　．‎ ‎【考点】复数代数形式的乘除运算．‎ ‎【专题】计算题；方程思想；数学模型法；数系的扩充和复数．‎ ‎【分析】把已知的等式变形，利用复数代数形式的乘除运算化简求得，再求其共轭复数得答案．‎ ‎【解答】解：由，得：‎ ‎，‎ ‎∴z=﹣3﹣4i．‎ 故答案为：﹣3﹣4i．‎ ‎【点评】本题考查复数代数形式的乘除运算，考查共轭复数的概念，是基础的计算题．‎ ‎　‎ ‎3．以点（1，2）为圆心，与直线4x+3y﹣35=0相切的圆的方程是　（x﹣1）2+（y﹣2）2=25　．‎ ‎【考点】圆的标准方程；直线与圆的位置关系．‎ ‎【专题】计算题．‎ ‎【分析】先求圆心到直线4x+3y﹣35=0的距离，再求出半径，即可由圆的标准方程求得圆的方程．‎ ‎【解答】解：以点（1，2）为圆心，与直线4x+3y﹣35=0相切，‎ 圆心到直线的距离等于半径，即：‎ 所求圆的标准方程：（x﹣1）2+（y﹣2）2=25‎ 故答案为：（x﹣1）2+（y﹣2）2=25‎ ‎【点评】本题考查圆的标准方程，直线与圆相切，是基础题．‎ ‎　‎ ‎4．数列所有项的和为　2　．‎ ‎【考点】等比数列的前n项和．‎ ‎【专题】计算题；转化思想；综合法；等差数列与等比数列．‎ ‎【分析】先求出数列前n项和，再求出前n项和的极限，从而求出结果．‎ ‎【解答】解：数列前n项和：‎ Sn==2[1﹣（）n]，‎ ‎∴数列所有项的和为：‎ S===2．‎ 故答案为：2．‎ ‎【点评】本题考查等比数列的前n项和的求法，是基础题，解题时要认真审题，注意等比数列的性质的合理运用．‎ ‎　‎ ‎5．已知矩阵A=，B=，AB=，则x+y=　8　．‎ ‎【考点】矩阵与矩阵的乘法的意义．‎ ‎【专题】计算题；转化思想；综合法；矩阵和变换．‎ ‎【分析】利用矩阵乘法法则求解．‎ ‎【解答】解：∵矩阵A=，B=，AB=，‎ ‎∴AB===，‎ ‎∴，解得x=5，y=3，‎ ‎∴x+y=8．‎ 故答案为：8．‎ ‎【点评】本题考查代数式的值的求法，是基础题，解题时要认真审题，注意矩阵乘法法则的合理运用．‎ ‎　‎ ‎6．等腰直角三角形的直角边长为1，则绕斜边旋转一周所形成的几何体的体积为　　．‎ ‎【考点】旋转体（圆柱、圆锥、圆台）．‎ ‎【专题】计算题；空间位置关系与距离；立体几何．‎ ‎【分析】直角边长为1的等腰直角三角形，绕斜边旋转一周所形成的几何体是两个底面半径为：，高也为的圆锥的组合体，代入圆锥体积公式，可得答案．‎ ‎【解答】解：直角边长为1的等腰直角三角形，‎ 绕斜边旋转一周所形成的几何体是两个底面半径为：，高也为的圆锥的组合体，‎ 故该几何体的体积V=2×[×]•=．‎ 故答案为：‎ ‎【点评】本题考查的知识点是旋转体，圆锥的体积，难度不大，属于基础题．‎ ‎　‎ ‎7．若（x﹣）9的展开式中x3的系数是﹣84，则a=　1　．‎ ‎【考点】二项式系数的性质．‎ ‎【专题】计算题．‎ ‎【分析】利用二项展开式的通项公式求出第r+1项，令x的指数为3得展开式中x3的系数，列出方程解得．‎ ‎【解答】解：展开式的通项为=（﹣a）rC9rx9﹣2r 令9﹣2r=3得r=3‎ ‎∴展开式中x3的系数是C93（﹣a）3=﹣84a3=﹣84，‎ ‎∴a=1．‎ 故答案为1‎ ‎【点评】本试题主要考查二项展开式的通项公式和求指定项系数的方法．‎ ‎　‎ ‎8．抛物线y2=12x的准线与双曲线的两条渐近线所围成的三角形的面积等于　　．‎ ‎【考点】双曲线的简单性质；抛物线的简单性质．‎ ‎【专题】圆锥曲线的定义、性质与方程．‎ ‎【分析】写出抛物线y2=12x的准线与双曲线的两条渐近线方程是解决本题的关键，然后确定三角形的形状和边长利用面积公式求出三角形的面积．‎ ‎【解答】解：抛物线y2=12x的准线为x=﹣3，‎ 双曲线的两条渐近线方程分别为：y=x，y=﹣x，‎ 这三条直线构成边长为2的等边三角形，‎ 因此，所求三角形面积等于×2×2×sin60°=．‎ 故答案为：．‎ ‎【点评】本题考查三角形形状的确定和面积的求解，考查双曲线标准方程与其渐近线方程的联系，抛物线标准方程与其准线方程的联系，考查学生直线方程的书写，考查学生分析问题解决问题的能力，属于基本题型．‎ ‎　‎ ‎9．已知ω，t＞0，函数的最小正周期为2π，将f（x）的图象向左平移t个单位，所得图象对应的函数为偶函数，则t的最小值为　　．‎ ‎【考点】三角函数中的恒等变换应用；正弦函数的图象；二阶矩阵．‎ ‎【专题】计算题；函数思想；数学模型法；三角函数的图像与性质．‎ ‎【分析】由题意得到函数解析式，利用辅助角公式化积后结合周期求得ω，再由函数图象的平移求得平移后的函数解析式，结合平移后的函数为偶函数求出t的取值集合得答案．‎ ‎【解答】解： ==．‎ ‎∵f（x）的最小正周期为2π，∴，得ω=1．‎ 将f（x）的图象向左平移t个单位，得f（x+t）=．‎ ‎∵函数f（x+t）为偶函数，‎ ‎∴，则t=．‎ 取k=0时，t的最小值为．‎ 故答案为：．‎ ‎【点评】本题考查三角函数中的恒等变换应用，考查了三角函数的图象平移，训练了函数奇偶性的求法，是中档题．‎ ‎　‎ ‎10．两个三口之家，共4个大人，2个小孩，约定星期日乘“奥迪”、“捷达”两辆轿车结伴郊游，每辆车最多只能乘坐4人，其中两个小孩不能独坐一辆车，则不同的乘车方法种数是　48　．‎ ‎【考点】排列、组合及简单计数问题．‎ ‎【专题】计算题．‎ ‎【分析】只需选出乘坐奥迪车的人员，剩余的可乘坐捷达．再分奥迪车上没有小孩、奥迪车上有一个小孩、奥迪车上有2个小孩这三种情况，分别求得乘车的方法数，相加即得所求．‎ ‎【解答】解：只需选出乘坐奥迪车的人员，剩余的可乘坐捷达．‎ 若奥迪车上没有小孩，则有=10种方法；‎ 若奥迪车上有一个小孩，则有=28种；‎ 若奥迪车上有两个小孩，则有=10种．‎ 综上，不同的乘车方法种数为10+28+10=48种，‎ 故答案为 48．‎ ‎【点评】本题主要考查排列与组合及两个基本原理的应用，体现了分类讨论的数学思想，属于中档题．‎ ‎　‎ ‎11．向量，满足，，与的夹角为60°，则=　　．‎ ‎【考点】平面向量数量积的运算．‎ ‎【专题】方程思想；综合法；平面向量及应用．‎ ‎【分析】求出，对两边平方，解出||．‎ ‎【解答】解： =||×=||．‎ ‎∵，∴（）2=．∴﹣2+=．∴1﹣||+||2=．解得||=．‎ 故答案为：．‎ ‎【点评】本题考查了平面向量的数量积运算，是基础题．‎ ‎　‎ ‎12．数列，则是该数列的第　128　项．‎ ‎【考点】数列的概念及简单表示法；数列的函数特性．‎ ‎【专题】等差数列与等比数列．‎ ‎【分析】该数列中：分子、分母之和为2的有1项，为3的有2项，为4的有3项，为5的有4项，…，由此可知：分子、分母之和为16的有15项．而分子、分母之和为17的有16项，排列顺序为：，，，，…，，；即可得出是分子、分母之和为17的第8项．‎ ‎【解答】解：观察数列，‎ 该数列中：分子、分母之和为2的有1项，为3的有2项，为4的有3项，为5的有4项，…，‎ ‎∴分子、分母之和为16的有15项．‎ 而分子、分母之和为17的有16项，排列顺序为：‎ ‎，，，，…，，；其中是分子、分母之和为17的第8项；．‎ 故共有项．‎ 故答案为128．‎ ‎【点评】本题考查了通过观察所要解决的提问转化为利用等差数列的前n项和公式解决，属于中档题．‎ ‎　‎ ‎13．已知直线（1﹣a）x+（a+1）y﹣4（a+1）=0（其中a为实数）过定点P，点Q在函数的图象上，则PQ连线的斜率的取值范围是　[﹣3，+∞）　．‎ ‎【考点】恒过定点的直线；直线的斜率．‎ ‎【专题】直线与圆．‎ ‎【分析】直线方程即 x+y﹣4+a（﹣x+y﹣4）=0，由，求得定点P的坐标，设点Q（m，m+），m≠0，则PQ连线的斜率为为=﹣3，再利用二次函数的性质求得它的范围．‎ ‎【解答】解：已知直线（1﹣a）x+（a+1）y﹣4（a+1）=0即 x+y﹣4+a（﹣x+y﹣4）=0，‎ 由，解得，故定点P的坐标为（0，4）．‎ 设点Q（m，m+），m≠0，则PQ连线的斜率为=1+﹣=﹣3≥﹣3，‎ 故PQ连线的斜率的取值范围为[﹣3，+∞），‎ 故答案为[﹣3，+∞）．‎ ‎【点评】本题主要考查直线过定点问题，直线的斜率公式，二次函数的性质应用，属于中档题．‎ ‎　‎ ‎14．如图，已知抛物线y2=x及两点A1（0，y1）和A2（0，y2），其中y1＞y2＞0．过A1，A2分别作y轴的垂线，交抛物线于B1，B2两点，直线B1B2与y轴交于点A3（0，y3），此时就称A1，A2确定了A3．依此类推，可由A2，A3确定A4，…．记An（0，yn），n=1，2，3，…．‎ 给出下列三个结论：‎ ‎①数列{yn}是递减数列；‎ ‎②对∀n∈N*，yn＞0；‎ ‎③若y1=4，y2=3，则．‎ 其中，所有正确结论的序号是　①②③　．‎ ‎【考点】数列与解析几何的综合．‎ ‎【专题】计算题；压轴题．‎ ‎【分析】先确定直线Bn﹣1Bn﹣2的方程，求得，由此即可得到结论．‎ ‎【解答】解：由题意，Bn﹣1（），Bn﹣2（），则直线Bn﹣1Bn﹣2的方程为 令x=0，则，∴‎ ‎∴‎ ‎∴‎ ‎∵y1＞y2＞0，∴yn＞0，故②正确；‎ ‎，∴yn＜yn﹣1，故①正确；‎ 若y1=4，y2=3，则，y4=，，故③正确．‎ 故答案为：①②③．‎ ‎【点评】本题考查数列与解析几何的综合，考查学生分析解决问题的能力，属于中档题．‎ ‎　‎ 二．选择题（本大题满分20分）本大题共有4题，每题都给出代号为A、B、C、D的四个结论，其中有且只有一个结论是正确的．必须用2B铅笔将正确结论的代号涂黑，选对得5分，不选、选错或者选出的代号超过一个，一律得零分．‎ ‎15．如图，该程序运行后输出的结果为（　　）‎ A．1 B．2 C．4 D．16‎ ‎【考点】程序框图．‎ ‎【专题】计算题；图表型．‎ ‎【分析】由题意可得：①a=1≤3，b=2，a=1+1=2；②a=2≤3，b=4，a=2+1=3；③a=3≤3，b=16，a=3+1=4；进而程序结束得到答案．‎ ‎【解答】解：由题意可得：①a=1≤3，b=2，a=1+1=2；‎ ‎②a=2≤3，b=4，a=2+1=3；‎ ‎③a=3≤3，b=16，a=3+1=4；‎ 因为a=4≤3不成立，所以输出b的数值为16．‎ 故选D．‎ ‎【点评】本题考查的知识点是程序框图，模拟循环的执行过程是解答此类问题常用的办法．‎ ‎　‎ ‎16．P是△ABC所在平面内一点，若，其中λ∈R，则P点一定在（　　）‎ A．△ABC内部 B．AC边所在直线上 C．AB边所在直线上 D．BC边所在直线上 ‎【考点】向量在几何中的应用．‎ ‎【专题】平面向量及应用．‎ ‎【分析】根据，代入，根据共线定理可知与共线，从而可确定P点一定在AC边所在直线上．‎ ‎【解答】解：∵，，‎ ‎∴=，则，‎ ‎∴∥，即与共线，‎ ‎∴P点一定在AC边所在直线上，‎ 故选B．‎ ‎【点评】本题主要考查向量的共线定理，要证明三点共线时一般转化为证明向量的共线问题．属于中档题．‎ ‎　‎ ‎17．若a，b是异面直线，则下列命题中的假命题为（　　）‎ A．过直线a可以作一个平面并且只可以作一个平面α与直线b平行 B．过直线a至多可以作一个平面α与直线b垂直 C．唯一存在一个平面α与直线a、b等距 D．可能存在平面α与直线a、b都垂直 ‎【考点】空间中直线与直线之间的位置关系．‎ ‎【专题】计算题；转化思想；综合法；空间位置关系与距离．‎ ‎【分析】在A中，把直线b平移与直线a相交，确定一个平面平行于b；在B中，只有a、b垂直时才能作出一个平面α与直线b垂直；在C中，由唯一性定理得唯一存在一个平面α与直线a、b等距；在D中：若存在平面α与直线a、b都垂直，则a∥b．‎ ‎【解答】解：由a，b是异面直线，知：‎ 在A中：a，b是两异面直线，把直线b平移与直线a相交，确定一个平面，因此经过直线a只能作出1个平面平行于b，故A正确；‎ 在B中：只有a、b垂直时才能作出一个平面α与直线b垂直，否则过直线a不可以作一个平面α与直线b垂直，故B正确；‎ 在C中：由唯一性定理得唯一存在一个平面α与直线a、b等距，故C正确；‎ 在D中：若存在平面α与直线a、b都垂直，则直线与平面垂直的性质定理得a∥b，故D错误．‎ 故选：D．‎ ‎【点评】本题考查命题真假的判断，是中档题，解题时要认真审题，注意空间中线线、线面、面面间的位置关系的合理运用．‎ ‎　‎ ‎18．王先生购买了一部手机，欲使用中国移动“神州行”卡或加入联通的130网，经调查其收费标准见下表：（注：本地电话费以分为计费单位，长途话费以秒为计费单位．）‎ 网络 月租费 本地话费 长途话费 甲：联通130‎ ‎12元 ‎0.36元/分 ‎0.06元/秒 乙：移动“神州行”‎ 无 ‎0.60元/分 ‎0.07元/秒 若王先生每月拨打本地电话的时间是拨打长途电话时间的5倍，若要用联通130应最少打多长时间的长途电话才合算．（　　）‎ A．300秒 B．400秒 C．500秒 D．600秒 ‎【考点】函数与方程的综合运用；函数的值；分段函数的应用．‎ ‎【专题】计算题；转化思想；函数的性质及应用．‎ ‎【分析】根据每月的通话时间和甲方式的收费标准，可知所需花费=月租费+本地话费+长途话费，可求所需话费y（元）与通话时间x（分钟）的函数关系式；将乙方式所需话费y（元）与通话时间x（分钟）的函数关系式求出，将两个式子进行比较，可得出较为省钱的入网方式．‎ ‎【解答】解：每月接打本地电话的时间是接打长途电话的5倍，王先生每月拨打长途电话时间为x（分钟），他所需话费y（元），联通130他所需话费y（元）与通话时间x（分钟）的函数关系式为y=12+0.36×5x+3.6x（x＞0）；‎ 移动“神州行”他所需话费y（元）与通话时间x（分钟）的函数关系式为：y=0.6×5x+4.2x，‎ 若要用联通130应最少打多长时间的长途电话才合算，可得：12+0.36×5x+3.6x＜0.6×5x+4.2x，‎ 解得：x＞（分钟）=400秒．‎ 故选：B．‎ ‎【点评】本题主要是应用数学模型来解决实际问题，考查一次函数的应用．‎ ‎　‎ 三．解答题（本大题满分74分）本大题共有5题，解答下列各题必须写出必要的步骤，答题务必写在黑色矩形边框内．‎ ‎19．在三棱锥P﹣ABC中，已知PA，PB，PC两两垂直，PB=5，PC=6，三棱锥P﹣ABC的体积为20，Q是BC的中点，求异面直线PB，AQ所成角的大小（结果用反三角函数值表示）．‎ ‎【考点】异面直线及其所成的角．‎ ‎【专题】计算题；转化思想；综合法；空间角．‎ ‎【分析】由三棱锥P﹣ABC的体积为20，得PA=4，取PC的中点为D，连结AD，DQ，则∠AQD为异面直线PB，AQ所成的角，由此能求出异面直线PB，AQ所成的角．‎ ‎【解答】解：∵在三棱锥P﹣ABC中，PA，PB，PC两两垂直，PB=5，PC=6，三棱锥P﹣ABC的体积为20，‎ ‎∴，解得PA=4，‎ 取PC的中点为D，连结AD，DQ，‎ 则∠AQD为异面直线PB，AQ所成的角，‎ ‎，DA=5，‎ ‎∵QD⊥平面PAC，∴QD⊥AD，‎ ‎∴tan∠AQD=2，‎ ‎∴异面直线PB，AQ所成的角为arctan2．‎ ‎【点评】本题考查异面直线所成角的求法，是基础题，解题时要认真审题，注意空间能力的培养．‎ ‎　‎ ‎20．设a、b、c分别是△ABC三个内角∠A、∠B、∠C的对边，若向量，且，‎ ‎（1）求tanA•tanB的值；‎ ‎（2）求的最大值．‎ ‎【考点】三角函数的化简求值；平面向量数量积的运算．‎ ‎【专题】计算题．‎ ‎【分析】（1）由，化简得 4cos（A﹣B）=5cos（A+B），由此求得tanA•tanB的值．‎ ‎（2）利用正弦定理和余弦定理化简为，而，利用基本不等式 求得它的最小值等于，从而得到tanC有最大值，从而求得所求式子的最大值．‎ ‎【解答】解：（1）由，得．…‎ 即 ，‎ 亦即 4cos（A﹣B）=5cos（A+B），…‎ 所以 ．…‎ ‎（2）因，…‎ 而，‎ 所以，tan（A+B）有最小值，… ‎ ‎ 当且仅当时，取得最小值．‎ 又tanC=﹣tan（A+B），则tanC有最大值，故的最大值为．…‎ ‎【点评】本题主要考查两个向量数量积公式，正弦定理和余弦定理，两角和的正切公式，以及基本不等式的应用，属于中档题．‎ ‎　‎ ‎21．某市2013年发放汽车牌照12万张，其中燃油型汽车牌照10万张，电动型汽车2万张．为了节能减排和控制总量，从2013年开始，每年电动型汽车牌照按50%增长，而燃油型汽车牌照每一年比上一年减少0.5万张，同时规定一旦某年发放的牌照超过15万张，以后每一年发放的电动车的牌照的数量维持在这一年的水平不变．‎ ‎（1）记2013年为第一年，每年发放的燃油型汽车牌照数构成数列{an}，每年发放的电动型汽车牌照数为构成数列{bn}，完成下列表格，并写出这两个数列的通项公式；‎ a1=10‎ a2=9.5‎ a3=　9　‎ a4=　8.5　‎ ‎…‎ b1=2‎ b2=　3　‎ b3=　4.5　‎ ‎ b4=　6.75　‎ ‎…‎ ‎（2）从2013年算起，累计各年发放的牌照数，哪一年开始超过200万张？‎ ‎【考点】数列的应用．‎ ‎【专题】应用题；点列、递归数列与数学归纳法．‎ ‎【分析】（1）利用从2013年开始，每年电动型汽车牌照按50%增长，而燃油型汽车牌照每一年比上一年减少0.5万张，同时规定一旦某年发放的牌照超过15万张，以后每一年发放的电动车的牌照的数量维持在这一年的水平不变，可填写表格，并写出这两个数列的通项公式；‎ ‎（2）利用等差数列与等比数列的求和公式，可得﹣n2+17n﹣≥200，即可得出结论．‎ ‎【解答】解：（1）‎ a1=10‎ a2=9.5‎ a3=9 ‎ a4=8.5 ‎ ‎…‎ b1=2‎ b2=3‎ b3=4.5 ‎ b4=6.75 ‎ ‎…‎ ‎…‎ 当1≤n≤20且n∈N*，an=10+（n﹣1）×（﹣0.5）=﹣0.5n+10.5；‎ 当n≥21且n∈N*，an=0．‎ ‎∴an=…‎ 而a4+b4=15.25＞15‎ ‎∴bn=，…‎ ‎（2）当n=4时，Sn=a1+a2+a3+a4+b1+b2+b3+b4=53.25．‎ 当5≤n≤21时，Sn=（a1+a2+…+an）+（b1+b2+b3+b4+b5+…+bn）=10n+++6.75（n﹣4）‎ ‎=﹣n2+17n﹣…‎ 由Sn≥200得﹣n2+17n﹣≥200，即n2﹣68n+843≤0，得34﹣≤n≤21 …‎ ‎∴到2029年累积发放汽车牌照超过200万张．…‎ ‎【点评】本题考查数列的应用，考查利用数学知识解决实际问题，考查数列的求和，考查学生分析解决问题的能力，属于中档题．‎ ‎　‎ ‎22．已知椭圆+y2=1上两个不同的点A，B关于直线对称．‎ ‎（1）若已知，M为椭圆上动点，证明：；‎ ‎（2）求实数m的取值范围；‎ ‎（3）求△AOB面积的最大值（O为坐标原点）．‎ ‎【考点】椭圆的简单性质．‎ ‎【专题】数形结合；方程思想；转化思想；圆锥曲线的定义、性质与方程．‎ ‎【分析】（1）设M（x，y），则+y2=1，利用两点之间的距离公式、二次函数的单调性即可得出．‎ ‎（2）由题意知m≠0，可设直线AB的方程为．与椭圆方程联立得．△＞0，再利用中点坐标公式、根与系数的关系即可得出．‎ ‎（3）利用弦长公式、点到直线的距离公式可得S△AOB，再利用二次函数的单调性即可得出．‎ ‎【解答】（1）证明：设M（x，y），则+y2=1，‎ 于是===，‎ ‎∵﹣1≤y≤1，‎ ‎∴当时，．即．‎ ‎（2）解：由题意知m≠0，可设直线AB的方程为．‎ 由消去y，得．‎ ‎∵直线与椭圆有两个不同的交点，‎ ‎∴，‎ 即 ①‎ 将AB中点，‎ 代入直线方程解得 ②‎ 由①②得或．‎ ‎（3）解：令，即，‎ 则，‎ 且O到直线AB的距离为，‎ 设△AOB的面积为S（t），∴，‎ 当且仅当时，等号成立．‎ 故△AOB面积的最大值为．‎ ‎【点评】本题考查了椭圆的定义及其标准方程、直线与椭圆相交弦长问题、点到直线的距离公式、三角形面积计算公式、轴对称问题、两点之间的距离公式，考查了推理能力与计算能力，属于难题．‎ ‎　‎ ‎23．已知函数f（x）=logkx（k为常数，k＞0且k≠1），且数列{f（an）}是首项为4，公差为2的等差数列．‎ ‎（1）求证：数列{an}是等比数列；‎ ‎（2）若bn=an+f（an），当时，求数列{bn}的前n项和Sn的最小值；‎ ‎（3）若cn=anlgan，问是否存在实数k，使得{cn}是递增数列？若存在，求出k的范围；若不存在，说明理由．‎ ‎【考点】数列与函数的综合；对数函数的图像与性质．‎ ‎【专题】分类讨论；定义法；函数的性质及应用；等差数列与等比数列．‎ ‎【分析】（1）运用等差数列的通项公式和对数的定义，可得an=k2n+2，再由等比数列的定义即可得证；‎ ‎（2）求得an，f（an），再由等差数列和等比数列的求和公式，运用单调性即可得到最小值；‎ ‎（3）由题意可得（n+1）lgk＜（n+2）•k2•lgk对一切n∈N*成立．讨论k＞1，0＜k＜1，运用数列的单调性即可得到所求k的范围．‎ ‎【解答】解：（1）证明：由题意可得f（an）=4+2（n﹣1）=2n+2，‎ 即logkan=2n+2，‎ ‎∴，‎ ‎∴．‎ ‎∵常数k＞0且k≠1，∴k2为非零常数，‎ ‎∴数列{an}是以k4为首项，k2为公比的等比数列；‎ ‎（2）当时，，f（an）=2n+2，‎ 所以，‎ 因为n≥1，所以，是递增数列，‎ 因而最小值为S1=1+3+﹣=．‎ ‎（3）由（1）知，，‎ 要使cn＜cn+1对一切n∈N*成立，‎ 即（n+1）lgk＜（n+2）•k2•lgk对一切n∈N*成立．‎ 当k＞1时，lgk＞0，n+1＜（n+2）k2对一切n∈N*恒成立；‎ 当0＜k＜1时，lgk＜0，n+1＞（n+2）k2对一切n∈N*恒成立，‎ 只需，‎ ‎∵单调递增，‎ ‎∴当n=1时，．‎ ‎∴，且0＜k＜1，∴．‎ 综上所述，存在实数满足条件．‎ ‎【点评】本题考查等差数列和等比数列的通项公式和求和公式的运用，考查数列的单调性的判断和运用，以及数列不等式恒成立问题的解法，属于中档题．‎ ‎　‎