高考模拟试卷 13页

‎ 2017年高考模拟试卷(1)‎ 南通市数学学科基地命题 ‎ 第Ⅰ卷（必做题，共160分） ‎ 一、填空题：本大题共14小题，每小题5分，共70分 ． ‎ ‎1． 已知， ，则 ▲ ． ‎ ‎2． 已知复数z满足，则复数z的实部为 ▲ ． ‎ ‎3． 函数 的单调增区间是 ▲ ．‎ ‎4． 将一颗质地均匀的正方体骰子（每个面上分别写有数字1，2，3，4，5，6）先后抛掷2次，观 察向上的点数，则点数之和是6的的概率是 ▲ ．‎ Read x If Then ‎ ‎ Else ‎ ‎ End if Print y ‎（第5题）‎ ‎5． 执行如图所示的伪代码，若输出的y的值为13，则输入的x的值是 ▲ ．‎ ‎6． 一种水稻品种连续5年的平均单位面积产量（单位：t/hm2）分别为：‎ ‎9.4，9.7，9.8，10.3，10.8，则这组样本数据的方差为 ▲ ．‎ ‎7． 已知函数．若为函数的一个零点，为函数图象的一条对称轴，则的值为 ▲ ．‎ ‎8． 已知，且，则a与b的夹角为 ▲ ．‎ ‎9． 已知，且，，则的值为 ▲ ．‎ ‎10．已知关于的一元二次不等式的解集为，其中为常数．则不等式 的解集为 ▲ ．‎ ‎11．已知正数，满足，则的最小值为 ▲ ．‎ ‎12．在平面直角坐标系中，已知圆C：，直线l：过定点A，且交圆C于点B，D，过点A作BC的平行线交CD于点E，则三角形AEC的周长为 ▲ ．‎ ‎13．设集合，集合 满足，且．若对任意的，，则为 ▲ ．‎ ‎14．定义：表示，中的较大者．设函数，‎ ‎ 若函数恰有4个零点，则实数的取值范围是 ▲ ．‎ 二、解答题：本大题共6小题，共90分.‎ ‎15．（本小题满分14分）‎ 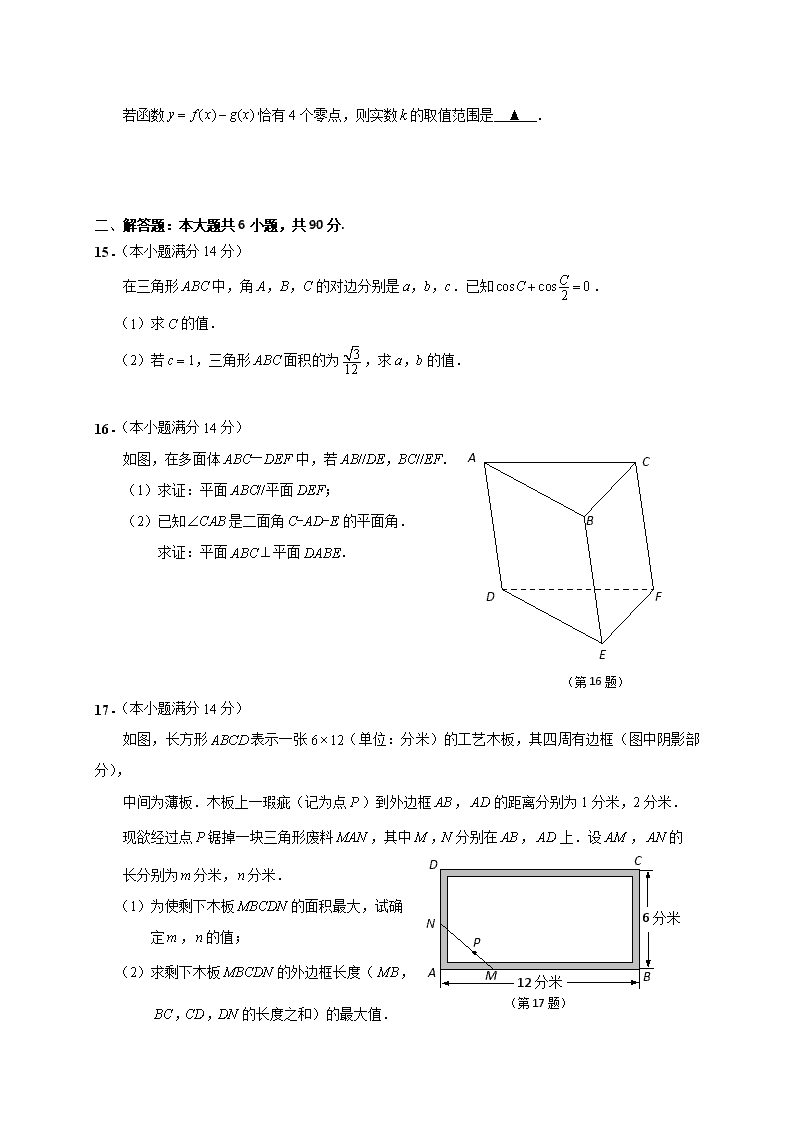在三角形ABC中，角A，B，C的对边分别是a，b，c．已知．‎ ‎ （1）求C的值．‎ ‎ （2）若c1，三角形ABC面积的为，求a，b的值．‎ ‎ ‎ ‎16．（本小题满分14分）‎ A F E D C B ‎（第16题）‎ 如图，在多面体ABC—DEF中，若AB//DE，BC//EF．‎ ‎（1）求证：平面ABC//平面DEF；‎ ‎（2）已知是二面角C-AD-E的平面角．‎ ‎ 求证：平面ABC平面DABE．‎ ‎17．（本小题满分14分）‎ 如图，长方形表示一张612（单位：分米）的工艺木板，其四周有边框（图中阴影部分），‎ 中间为薄板．木板上一瑕疵（记为点）到外边框，的距离分别为1分米，2分米．‎ 现欲经过点锯掉一块三角形废料，其中分别在，上．设A B D M N C ‎6分米 ‎12分米 P ‎（第17题）‎ ，的 长分别为分米，分米．‎ ‎ （1）为使剩下木板的面积最大，试确 ‎ 定，的值；‎ ‎ （2）求剩下木板的外边框长度（‎ ‎ 的长度之和）的最大值． ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎18．（本小题满分16分）‎ ‎ 如图，在平面直角坐标系中，设椭圆：（a＞1）.‎ ‎ （1）若椭圆的焦距为2，求a的值；‎ ‎ （2）求直线被椭圆截得的线段长（用a，k表示）；‎ x y O ‎（第18题）‎ ‎（3）若以A（0，1）为圆心的圆与椭圆总有4个公共点，求椭圆的离心率的 取值范围.‎ ‎19．（本小题满分16分）‎ ‎ 已知函数．‎ ‎（1）若函数为奇函数，且图象过点，求的解析式；‎ ‎（2）若和是函数的两个极值点．‎ ‎ ①求a，b的值；‎ ‎ ②求函数在区间上的零点个数．‎ ‎ ‎ ‎20．（本小题满分16分）‎ ‎ 设等差数列与等比数列共有个对应项相等．‎ ‎ （1）若，，试比较的大小；‎ ‎ （2）若，，求的值．‎ ‎ （3）若等比数列的公比，且，求证：．‎ ‎ 【参考结论】若上可导函数满足（），则，．‎ 第II卷（附加题，共40分）‎ ‎21.【选做题】本题包括A, B,C,D四小题，每小题10分，请选定其中两小题，并在相应的答题区域内作答.‎ A B F C D E ‎（第21 A题）‎ A，（选修4-1；几何证明选讲） 如图，四边形是圆的内接四边形，，的延长线交的延长线于点．求证：是四边形的外角的平分线． ‎ ‎ ‎ B．（选修4-2：矩阵与变换） ‎ ‎ 已知矩阵，，求矩阵AB的逆矩阵．‎ C．（选修4-4：坐标系与参数方程）在极坐标系中，求圆截直线 所得线段长．‎ D．（选修4-5：不等式选讲）求证：．‎ ‎【选做题】第22题、23题，每题10分，共计20分.‎ ‎22．在平面直角坐标系中，设点，，均在抛物线 上，且．‎ ‎ （1）求的值；‎ ‎ （2）试用表示；‎ ‎ （3）求直线与直线交点的纵坐标．‎ ‎23． （）个不同数随机排成如下的一个三角形：‎ ‎ ＊‎ ‎ ＊ ＊‎ ‎ ＊ ＊ ＊‎ ‎ ……………………‎ ‎＊ ＊ … ＊ ＊‎ ‎ ‎ ‎ ‎ ‎ 是从上往下数第行中的最大数，为的概率．‎ ‎ （1）求的值；‎ ‎ （2）猜想的表达式，并证明．‎ ‎2017年高考模拟试卷(1)参考答案 一、填空题 ‎1．．．‎ ‎2．． ，则复数z的实部为 ．‎ ‎3．（-9，+∞）．函数的单调增区间（-9，+∞）.‎ ‎4． ．点数之和是6包括共5种情况，则所 ‎ 求概率是．‎ ‎5． 8．若，则，不符；若，则．‎ ‎6． 0. 244．这组数据的平均数为10，方差为 ‎ .‎ ‎7． ．函数的周期，又，所以的值为.‎ ‎8． ．依题意，，又，故，则a与b的夹角为．‎ ‎9． ．．‎ ‎10． ．因为不等式的解集为，所以，且，即，则，则即为，从而，故解集为．‎ ‎11．3．由得，，则 ‎ ．‎ ‎12． 5．易得圆C：，定点A，，则，‎ ‎ 从而三角形AEC的周长为5．‎ ‎13． 2027．易得数列：1，3，5，6，7，9，10，11，12，13，14，15，17，…，‎ ‎ 则…，当，‎ ‎，从而第项为．‎ ‎14． ． 恰有4个零点，‎ 当 y y x x O O ‎1‎ ‎1‎ 时，与相切．如图，‎ ‎ 结合图形知，实数的取值范围是．‎ 二、解答题 ‎ ‎15． （1）因为，‎ ‎ 所以， ‎ ‎ 解得或， ‎ ‎ 又 ，故，‎ ‎ 从而，即． ‎ ‎ （2）由余弦定理得，‎ ‎ ， ① ‎ ‎ 由三角形ABC的面积得， ‎ ‎， ② ‎ ‎ 由①②得，． ‎ ‎16． （1）因为AB//DE，‎ ‎ 又AB平面DEF，‎ ‎ DE平面DEF，‎ ‎ 所以AB//平面DEF， ‎ ‎ 同理BC//平面DEF，‎ ‎ 又因为，‎ ‎ 平面ABC，‎ ‎ 所以平面ABC//平面DEF. ‎ ‎ （2）因为是二面角C-AD-E的平面角，‎ ‎ 所以 ‎ ‎ 又因为，‎ ‎ 平面ABC，‎ ‎ 所以DA平面ABC， ‎ ‎ 又DA平面DABE，‎ ‎ 所以平面ABC平面DABE. ‎ A B D M N C ‎6分米 ‎12分米 P ‎（第17题）‎ E F ‎17． （1）过点分别作，的垂线，垂足分别为，，‎ ‎ 则△与△相似，‎ ‎ 从而， ‎ ‎ 所以，‎ ‎ 即． ‎ ‎ 欲使剩下木板的面积最大，即要锯掉的三角形废料的面积 ‎ 最小．‎ ‎ 由得， （当且仅当，即，时，‎ ‎ “”成立），此时（平方分米）． ‎ ‎ （2）欲使剩下木板的外边框长度最大，即要最小．‎ ‎ 由（1）知，， ‎ ‎ （当且仅当即，时，“”成立），‎ 答：此时剩下木板的外边框长度的最大值为分米． ‎ ‎18． （1）由椭圆：（a＞1）知，‎ ‎ 焦距为，‎ ‎ 解得，‎ ‎ 因为a＞1，所以. ‎ ‎ （2）设直线被椭圆截得的线段长为，‎ ‎ 由得，‎ ‎ 解得，． ‎ ‎ 因此． ‎ ‎ （3）因为圆与椭圆的公共点有4个，由对称性可设轴左侧的椭圆上有2个不同的公共点为P，Q，满足．‎ 记直线AP，AQ的斜率分别为，，且，，．‎ 由（2）知，，，‎ ‎ 则， ‎ 所以，‎ 因为，，，‎ 所以，‎ 变形得，，‎ 从而，‎ 解得， ‎ ‎ 则． ‎ ‎19． （1）因为函数为偶函数，‎ ‎ 所以，即，‎ ‎ 整理得，，‎ ‎ 所以，从而，‎ ‎ 又函数图象过点，所以． ‎ ‎ 从而． ‎ ‎ （2）①的导函数．‎ ‎ 因为在和处取得极值，‎ 所以，‎ 即 解得． ‎ ‎ ②由（1）得，．‎ ‎ 列表：‎ x ‎0‎ ‎(0，1)‎ ‎1‎ ‎(1，2)‎ ‎2‎ ‎(2，3)‎ ‎3‎ + ‎0‎ - ‎0‎ + c 单调增 ‎5 + c 单调减 ‎4 + c 单调增 ‎9 + c 显然，函数在[0，3]上的图象是一条不间断的曲线．‎ 由表知，函数在[0，3]上的最小值为，最大值为． ‎ 所以当或（即）时，函数在区间上的零点个数为0．‎ 当时，因为，且函数在(0，1)上是单调增函数，‎ 所以函数在(0，1)上有1个零点．‎ 当时，因为，且在(1，2)上是单调减函数，‎ 所以函数在(1，2)上有1个零点．‎ 当时，因为，且在(2，3)上是单调增函数，‎ 所以函数在(2，3)上有1个零点．‎ 综上，当或时，函数在区间上的零点个数为0；‎ 当或时，零点个数为1；‎ 当或时，零点个数为2；‎ 当时，零点个数为3． ‎ ‎20．（1）依题意，‎ ‎ （当且仅当时，等号成立）． ‎ ‎ （2）易得，当为奇数时，，所以，‎ ‎ 又，故，此时； ‎ ‎ 当为偶数时，，所以，‎ ‎ 又，故…‎ ‎ 若，则，若，则， ‎ ‎ 下证：当，且为偶数时，，即．‎ ‎ 证明：记，则，‎ ‎ 所以在，且为偶数时单调递增，‎ ‎ 从而．‎ ‎ 综上，，所以的值为3． ‎ ‎ （3）证明：假设，不妨，满足，，，‎ ‎ 设，，其中，且，‎ ‎ 记，‎ ‎ 则，， 由参考结论，知，，，， ‎ ‎ 同理，，，即，‎ ‎ 这与矛盾，故假设不成立，从而． ‎ ‎ ‎ 第Ⅱ卷（附加题，共40分）‎ A．因为是圆的内接四边形，‎ ‎ 所以，． ‎ 因为，所以，‎ ‎ 所以，‎ ‎ 所以是四边形的外角的平分线． ‎ B．因为，，‎ ‎ 所以． ‎ 由逆矩阵公式得，． ‎ C．以极点O为原点，极轴Ox为x轴正半轴建立平面直角坐标系xOy．‎ ‎ 则圆化为普通方程，‎ ‎ 即． ‎ 直线化为普通方程，即． ‎ ‎ 圆心到直线的距离为，‎ ‎ 于是所求线段长为． ‎ D．由柯西不等式可得，‎ ‎ ， ‎ ‎ （当且仅当，即时，“=”成立．） ‎ ‎22． （1）依题意，将代入得，； ‎ ‎ （2）因为 ，‎ 所以，‎ ‎ 其中，，‎ ‎ 从而，‎ 化简得，； ‎ ‎ （3）易得直线的方程为，‎ ‎ 令得， ‎ ‎． ‎ ‎23．‎ 1‎ ‎2 3‎ ‎ 1‎ ‎3 2‎ ‎ 2‎ ‎1 3‎ ‎ 2‎ ‎3 1‎ ‎ 3‎ ‎1 2‎ ‎ 3‎ ‎2 1‎ 当时，1，2，3排成一个三角形有：‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 1‎ ‎2 3‎ ‎ 1‎ ‎3 2‎ ‎ 2‎ ‎1 3‎ ‎ 2‎ ‎3 1‎ ‎ 共有6种，其中满足的有如下4种：‎ ‎ ‎ ‎ 所以； ‎ ‎ （2）设当时，的概率为，‎ ‎ 则当时，的概率为，‎ ‎ 而排在第行的概率为，‎ ‎ 所以，即， 故，，，…，， ‎ ‎ 叠乘，得，其中，‎ ‎ 所以． ‎ ‎ ‎