高考数学一轮复习学案人教版A版97 抛物线答案 4页

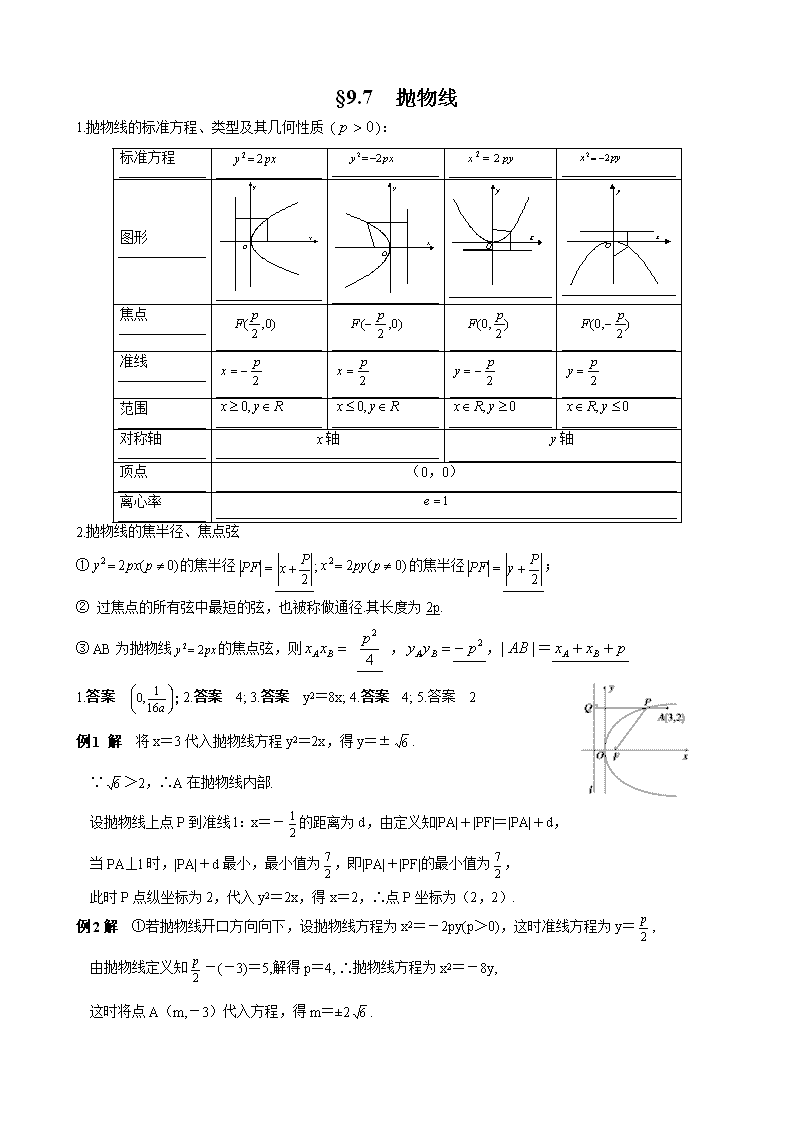
‎§9.7 抛物线 ‎1.抛物线的标准方程、类型及其几何性质 ()：‎ 标准方程 图形 焦点 准线 范围 对称轴 轴 轴 顶点 ‎ （0，0）‎ 离心率 ‎2.抛物线的焦半径、焦点弦 ‎①的焦半径;的焦半径；‎ ‎② 过焦点的所有弦中最短的弦，也被称做通径.其长度为2p.‎ ‎③ AB为抛物线的焦点弦，则 ，，＝‎ ‎1.答案 ; 2.答案 4; 3.答案 y2＝8x; 4.答案 4; 5.答案 2‎ 例1 解 将x＝3代入抛物线方程y2＝2x，得y＝±.‎ ‎∵＞2，∴A在抛物线内部.‎ 设抛物线上点P到准线l：x＝－的距离为d，由定义知|PA|＋|PF|＝|PA|＋d，‎ 当PA⊥l时，|PA|＋d最小，最小值为，即|PA|＋|PF|的最小值为，‎ 此时P点纵坐标为2，代入y2＝2x，得x＝2，∴点P坐标为（2，2）.‎ 例2解 ①若抛物线开口方向向下，设抛物线方程为x2＝－2py(p＞0)，这时准线方程为y＝,‎ 由抛物线定义知－(－3)＝5,解得p＝4, ∴抛物线方程为x2＝－8y,‎ 这时将点A（m,－3）代入方程，得m＝±2.‎ ‎②若抛物线开口方向向左或向右，可设抛物线方程为y2＝2ax (a≠0)，‎ 从p＝|a|知准线方程可统一成x＝－的形式，于是从题设有，‎ 解此方程组可得四组解,,，.‎ ‎∴y2＝2x,m＝；y2＝－2x,m＝－；y2＝18x,m＝；y2＝－18x,m＝－.‎ 例3(1)证明 由题意设A,B,x1＜x2, M.‎ 由x2＝2py得y＝,则y′＝,所以kMA＝,kMB＝. 2分 因此,直线MA的方程为y＋2p＝(x－x0),直线MB的方程为y＋2p＝(x－x0).‎ 所以,＋2 p ＝ (x1－x0), ①＋2 p ＝(x2－x0). ② 5分 由①、②得＝，因此，x0＝，即2x0＝.‎ 所以A、M、B三点的横坐标成等差数列. 8分 ‎（2）解 由（1）知，当x0＝2时，将其代入①、②，并整理得：x－4x1－4p2＝0，x－4x2－4 p 2＝0，‎ 所以，x1、x2是方程x2－4x－4 p 2＝0的两根， 10分因此，x1＋x2＝4，x1x2＝－4 p 2，‎ 又kAB＝＝＝，所以kAB＝. 12分 由弦长公式得：|AB|＝＝.‎ 又|AB|＝4，所以p＝1或p＝2，因此所求抛物线方程为x2＝2y或x2＝4y. 16分 ‎1.答案 ‎ ‎2.解 设抛物线的方程为y2＝2 p x(p＞0),其准线为x＝－.设A（x1,y1）,B(x2,y2),‎ ‎∵|AF|＋|BF|＝8，∴x1＋＋x2＋＝8，即x1＋x2＝8－p.‎ ‎∵Q（6，0）在线段AB的中垂线上，∴|QA|＝|QB|.即(x1－6)2＋y12＝(x2－6)2＋y22,‎ 又y12＝2px1,y22＝2px2,∴(x1－x2)(x1＋x2－12＋2p)＝0.∵AB与x轴不垂直，∴x1≠x2,‎ 故x1＋x2－12＋2p＝8－ p－12＋2 p＝0, 即p＝4.从而抛物线的方程为y2＝8x.‎ ‎3.解 （1）由题意可得直线l的方程为y＝x＋, ①‎ 过原点垂直于l的直线方程为y＝－2x. ② 解①②得x＝－.‎ ‎∵抛物线的顶点关于直线l的对称点在该抛物线的准线上，‎ ‎∴－＝－×2, p＝2.∴抛物线C的方程为y2＝4x.‎ ‎(2)设A(x1,y1),B(x2,y2),N(x,y),由题意知y＝y1. 由·＋ p 2＝0，得x1x2＋y1y2＋4＝0,‎ 又y12＝4x1,y22＝4x2,解得y1y2＝－8, ③ 直线ON：y＝x，即y＝x. ④ ‎ 由③、④及y＝y1得点N的轨迹方程为x＝－2(y≠0).‎ ‎1.答案x2＝8y; 2.答案;3.答案; 4.答案相等; 5.答案－; 6.答案6; 7.答案3＋2; 8.答案 ‎9.解 因为一直角边的方程是y＝2x, 所以另一直角边的方程是y＝－x.‎ 由，解得,或（舍去）， 由,解得,或（舍去）,‎ ‎∴三角形的另两个顶点为和（8 p,－4p）.∴＝2.‎ 解得p＝,故所求抛物线的方程为y2＝x.‎ ‎10.解由题设知，抛物线以双曲线的右焦点为焦点，准线过双曲线的左焦点，∴p＝2c.抛物线方程为y2＝4cx.‎ ‎∵抛物线过点，∴6＝4c·.∴c＝1，故抛物线方程为y2＝4x.‎ 又双曲线＝1过点， ∴＝1.又a2＋b2＝c2＝1.‎ ‎∴＝1.∴a2＝或a2＝9（舍）. ∴b2＝，故双曲线方程为4x2－＝1.‎ ‎11.（1）解 由已知得2 p＝8,∴＝2,∴抛物线的焦点坐标为F（2，0），准线方程为x＝－2.‎ ‎（2）证明 设A（xA，yA），B（xB，yB），直线AB的斜率为k＝tan,则直线方程为y＝k(x－2),‎ 将此式代入y2＝8x,得k2x2－4(k2＋2)x＋4k2＝0,故xA＋xB＝,‎ 记直线m与AB的交点为E（xE,yE)，则xE＝＝,yE＝k(xE－2)＝,‎ 故直线m的方程为y－＝－,令y＝0,得点P的横坐标xP＝＋4,‎ 故|FP|＝xP－2＝＝,∴|FP|－|FP|cos2＝(1－cos2)＝＝8,为定值.‎ ‎12.解 （1）设M（x,y）为轨迹上任意一点，A（0,b）,Q(a,0)(a≥0),‎ 则＝（x,y－b），＝(a－x,－y), ∵＝－，∴（x，y－b）＝－（a－x，－y），‎ ‎∴，从而.∴A，且＝, ＝.‎ ‎∵·＝0，∴·＝0，即3x－y2＝0,‎ ‎∴y2＝4x,故M点的轨迹方程为y2＝4x.‎ ‎(2)轨迹C的焦点为F（1，0），准线为l:x＝－1,对称轴为x轴.设直线m的方程为y＝k(x－1)(k≠0),‎ 由ky2－4y－4k＝0,‎ 设G（x1,y1）,H(x2,y2),‎ 则由根与系数的关系得，y1y2＝－4,‎ 又由已知＝（－1，y1),＝,‎ ‎∴(－1)×y2－y1×＝－y2－·y2＝－y2＋y2＝0,‎ ‎∴∥,故O，E，H三点共线.‎