高考数学试题分类汇编——三角函数2 31页

2010 年高考数学试题分类汇编——三角函数 （2010 上海文数）18.若△ 的三个内角满足 ，则△ （A）一定是锐角三角形. （B）一定是直角三角形. （C）一定是钝角三角形. (D)可能是锐角三角形，也可能是钝角三角形. 解析：由 及正弦定理得 a:b:c=5:11:13 由余弦定理得 ，所以角 C 为钝角 （2010 湖南文数）7.在△ABC 中，角 A，B，C 所对的边长分别为 a，b，c，若∠C=120°，c= a，则 A.a＞b B.a＜b C. a＝b D.a 与 b 的大小关系不能确定 【命题意图】本题考查余弦定理，特殊角的三角函数值，不等式的性质，比较法,属中档题。 （2010 浙江理数）（9）设函数 ，则在下列区间中函数 不存在 零点的是 （A） （B） （C） （D） 解析：将 的零点转化为函数 的交点，数形结合可知答 案选 A，本题主要考察了三角函数图像的平移和函数与方程的相关知识点，突出了对转化思 想和数形结合思想的考察，对能力要求较高，属较难题 （2010 浙江理数）（4）设 ，则“ ”是“ ”的 ABC sin :sin :sin 5:11:13A B C = ABC sin :sin :sin 5:11:13A B C = 01152 13115cos 222 <×× −+=c 2 ( ) 4sin(2 1)f x x x= + − ( )f x [ ]4, 2− − [ ]2,0− [ ]0,2 [ ]2,4 ( )xf ( ) ( ) ( ) xxhxxg =+= 与12sin4 0 2x π＜ ＜ 2sin 1x x＜ sin 1x x＜ （A）充分而不必要条件 （B）必要而不充分条件 （C）充分必要条件 （D）既不充分也不必要条件 解析：因为 0＜x＜ ，所以 sinx＜1，故 xsin2x＜xsinx，结合 xsin2x 与 xsinx 的取值范围相同， 可知答案选 B，本题主要考察了必要条件、充分条件与充要条件的意义，以及转化思想和处 理不等关系的能力，属中档题 （ 2010 全 国 卷 2 理 数 ）（ 7 ） 为 了 得 到 函 数 的 图 像 ， 只 需 把 函 数 的图像 （A）向左平移 个长度单位 （B）向右平移 个长度单位 （C）向左平移 个长度单位 （D）向右平移 个长度单位 【答案】B 【命题意图】本试题主要考查三角函数图像的平移. 【 解 析 】 = ， = ， 所 以 将 的图像向右平移 个长度单位得到 的图像，故选 B. （2010 陕西文数）3.函数 f (x)=2sinxcosx 是 [C] (A)最小正周期为 2π的奇函数 （B）最小正周期为 2π的偶函数 (C)最小正周期为π的奇函数 （D）最小正周期为π的偶函数 解析：本题考查三角函数的性质 f (x)=2sinxcosx=sin2x，周期为π的奇函数 （2010 辽宁文数）（6）设 ,函数 的图像向右平移 个单位后与 原图像重合，则 的最小值是 （A） （B） （C） （D） 3 解析：选 C.由已知，周期 （2010 辽宁理数）（5）设 >0,函数 y=sin( x+ )+2 的图像向右平移 个单位后与原图 像重合，则 的最小值是 （A） (B) (C) (D)3 sin(2 )3y x π= − sin(2 )6y x π= + 4 π 4 π 2 π 2 π sin(2 )6y x π= + sin 2( )12x π+ sin(2 )3y x π= − sin 2( )6x π= − sin(2 )6y x π= + 4 π sin(2 )3y x π= − 2 π 0ω > sin( ) 23y x πω= + + 4 3 π ω 2 3 4 3 3 2 2 4 3, .3 2T π π ωω= = ∴ = ω ω 3 π 3 4π ω 2 3 4 3 3 2 【答案】C 【命题立意】本题考查了三角函数图像的平移变换与三角函数的周期性，考查了同 学们对知识灵活掌握的程度。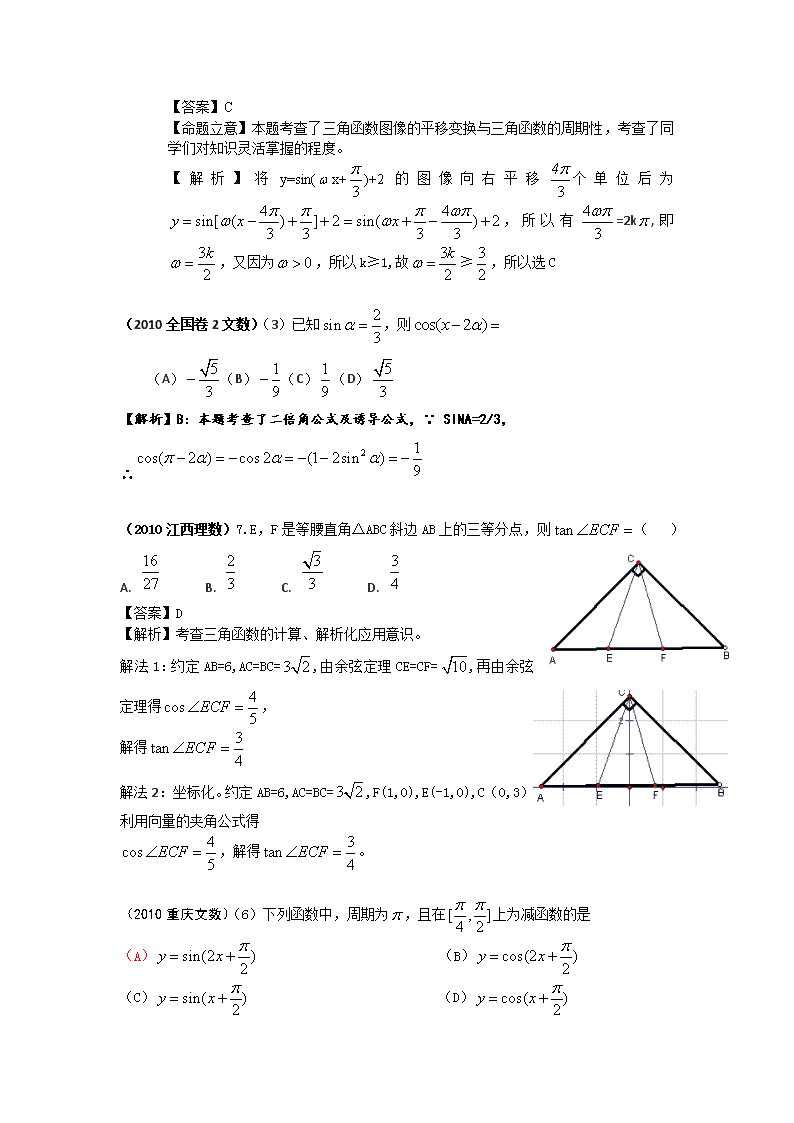 【 解 析 】 将 y=sin( x+ )+2 的 图 像 向 右 平 移 个 单 位 后 为 ， 所 以 有 =2k , 即 ，又因为 ，所以 k≥1,故 ≥ ，所以选 C （2010 全国卷 2 文数）（3）已知 ，则 （A） （B） （C） （D） 【解析】B：本题考查了二倍角公式及诱导公式，∵ SINA=2/3， ∴ （2010 江西理数）7.E，F 是等腰直角△ABC 斜边 AB 上的三等分点，则 （ ） A. B. C. D. 【答案】D 【解析】考查三角函数的计算、解析化应用意识。 解法 1：约定 AB=6,AC=BC= ,由余弦定理 CE=CF= ,再由余弦 定理得 ， 解得 解法 2：坐标化。约定 AB=6,AC=BC= ,F(1,0),E(-1,0),C（0,3） 利用向量的夹角公式得 ，解得 。 （2010 重庆文数）（6）下列函数中，周期为 ，且在 上为减函数的是 （A） （B） （C） （D） ω 3 π 3 4π 4sin[ ( ) ] 23 3y x π πω= − + + 4sin( ) 23 3x π ωπω= + − + 4 3 ωπ π 3 2 kω = 0ω > 3 2 kω = 3 2 2sin 3 α = cos( 2 )x α− = 5 3 − 1 9 − 1 9 5 3 2 1cos( 2 ) cos2 (1 2sin ) 9 π α α α− = − = − − = − tan ECF∠ = 16 27 2 3 3 3 3 4 3 2 10 4cos 5ECF∠ = 3tan 4ECF∠ = 3 2 4cos 5ECF∠ = 3tan 4ECF∠ = π [ , ]4 2 π π sin(2 )2y x π= + cos(2 )2y x π= + sin( )2y x π= + cos( )2y x π= + 解析：C、D 中函数周期为 2 ，所以错误 当 时， ，函数 为减函数 而函数 为增函数，所以选 A （2010 重庆理数） （6）已知函数 的部分 图象如题（6）图所示，则 A. =1 = B. =1 =- C. =2 = D. =2 = - 解析： 由五点作图法知 ， = - π [ , ]4 2x π π∈ 32 ,2 2x π ππ + ∈   sin(2 )2y x π= + cos(2 )2y x π= + ( )sin ( 0, )2y x πω ϕ ω ϕ= + > < ω ϕ 6 π ω ϕ 6 π ω ϕ 6 π ω ϕ 6 π 2=∴= ϖπT 232 πϕπ =+× ϕ 6 π （2010 山东文数）（10）观察 ， ， ，由归纳推理可得：若定义在 上的函数 满足 ，记 为 的导函数，则 = （A） (B) (C) (D) 答案：D （2010 北京文数）（7）某班设计了一个八边形的班徽（如 图），它由腰长 为 1， 顶角为 的四个等腰三角形，及其底边构成的正方形所组 成， 该八边形的面积为 （A） ； （B） （C） ； （D） 答案：A （2010 四川理数）（6）将函数 的图像上所有的点向右平行移动 个单位长度，再把所得各点的 横坐标伸长到原来的 2 倍（纵坐标不变），所得图像的函数解析式是 w_w w. k#s5_u.c o*m （A） （B） w_w_w.k*s 5*u.c o*m （C） （D） 解析：将函数 的图像上所有的点向右平行移动 个单位长度，所得函数图象的解析式为 y＝sin(x － ) w_w_w.k*s 5*u.c o*m 再 把 所 得 各 点 的 横 坐 标 伸 长 到 原 来 的 2 倍 （ 纵 坐 标 不 变 ），所 得 图 像 的 函 数 解 析 式 是 . 答案：C （2010 天津文数）（8） 为了得到这个函数的图象，只 要将 的图象上所有的点 (A)向左平移 个单位长度，再把所得各点的横坐标缩短 到 原来的 倍，纵坐标不变 2 '( ) 2x x= 4 ' 3( ) 4x x= '(cos ) sinx x= − R ( )f x ( ) ( )f x f x− = ( )g x ( )f x ( )g x− ( )f x ( )f x− ( )g x ( )g x− α 2sin 2cos 2α α− + sin 3 cos 3α α− + 3sin 3 cos 1α α− + 2sin cos 1α α− + siny x= 10 π sin(2 )10y x π= − sin(2 )5y x π= − 1sin( )2 10y x π= − 1sin( )2 20y x π= − siny x= 10 π 10 π 1sin( )2 10y x π= − 5y Asin x x R 6 6 π πω ϕ  = ∈   右图是函数 （ + ）（ ）在区间 - ， 上的图象， y sin x x R= ∈（ ） 3 π 1 2 (B) 向左平移 个单位长度，再把所得各点的横坐标伸长到原来的 2 倍，纵坐标不变 (C) 向左平移 个单位长度，再把所得各点的横坐标缩短到原来的 倍，纵坐标不变 (D) 向左平移 个单位长度，再把所得各点的横坐标伸长到原来的 2 倍，纵坐标不变 【答案】A 【解析】本题主要考查三角函数的图像与图像变换的基础知识，属于中等题。 由图像可知函数的周期为 ，振幅为 1，所以函数的表达式可以是 y=sin(2x+ ).代入（- ，0）可得 的 一个值为 ，故图像中函数的一个表达式是 y=sin(2x+ )，即 y=sin2(x+ )，所以只需将 y=sinx（x∈R） 的图像上所有的点向左平移 个单位长度，再把所得各点的横坐标缩短到原来的 倍，纵坐标不变。 【温馨提示】根据图像求函数的表达式时，一般先求周期、振幅，最后求 。三角函数图像进行平移变换 时注意提取 x 的系数，进行周期变换时，需要将 x 的系数变为原来的 （ 2010 天 津 理 数 ）（ 7 ） 在 △ ABC 中 ， 内 角 A,B,C 的 对 边 分 别 是 a,b,c ， 若 ， ，则 A= （A） （B） （C） （D） 【答案】A 【解析】本题主要考查正弦定理与余弦定理的基本应用，属于中等题。 由由正弦定理得 ， 所以 cosA= = ，所以 A=300 【温馨提示】解三角形的基本思路是利用正弦、余弦定理将边化为角运算或将角化为边运算。 （2010 福建文数） 3 π 6 π 1 2 6 π π ϕ 6 π ϕ 3 π 3 π 6 π 6 π 1 2 ϕ 1 ω 2 2 3a b bc− = sin 2 3sinC B= 030 060 0120 0150 2 3 2 32 2 c b c bR R = ⇒ = 2 2 2 2+c -a 3 2 2 b bc c bc bc − += 3 2 3 3 2 2 bc bc bc − + = （2010 福建文数）2．计算 的结果等于( ) A． B． C． D． 【答案】B 【解析】原式= ,故选 B． 【命题意图】本题三角变换中的二倍角公式,考查特殊角的三角函数值 （2010 全国卷 1 文数） (1) (A) (B)- (C) (D) 1.C【命题意图】本小题主要考查诱导公式、特殊三角函数值等三角函数知识 【解析】 （2010 全国卷 1 理数）(2)记 ,那么 A. B. - C. D. - （2010 四川文数）（7）将函数 的图像上所有的点向右平行移动 个单位长度，再把所得各 点的横坐标伸长到原来的 2 倍（纵坐标不变），所得图像的函数解析式是高^考#资*源^网 （A） （B） 1 2sin 22.5−  1 2 2 2 3 3 3 2 2cos45 = 2  cos300° = 3 2 − 1 2 1 2 3 2 ( ) 1cos300 cos 360 60 cos60 2 ° = °− ° = ° = cos( 80 ) k− ° = tan100° = 21 k k − 21 k k − 21 k k− 21 k k− siny x= 10 π sin(2 )10y x π= − y = sin(2 )5x π− （C） （D） 解析：将函数 的图像上所有的点向右平行移动 个单位长度，所得函数图象的解析式为 y＝sin(x － )w_w w. k#s5_u.c o*m 再 把 所 得 各 点 的 横 坐 标 伸 长 到 原 来 的 2 倍 （ 纵 坐 标 不 变 ），所 得 图 像 的 函 数 解 析 式 是 . 答案：C （2010 湖北文数）2.函数 f(x)= 的最小正周期为 A. B.x C.2 D.4 【答案】D 【解析】由 T=| |=4π，故 D 正确. （2010 湖南理数）6、在△ABC 中，角 A，B，C 所对的边长分别为 a,b,c，若∠C=120°， ,则 A、a>b B、a0)6 πω ω g(x)=2cos(2x+ )+1ϕ x [0, ]2 π∈ f(x) 3[- ,3]2 2ω = x [0, ]2 π∈ 52x- [- , ]6 6 6 π π π∈ f(x) 33sin (- )=-6 2 π 3sin =32 π f(x) 3[- ,3]2      20 π , 2 3 2 3 6cosb a Ca b + = tan tan tan tan C C A B + [解析] 考查三角形中的正、余弦定理三角函数知识的应用，等价转化思想。一题多解。 （方法一）考虑已知条件和所求结论对于角 A、B 和边 a、b 具有轮换性。 当 A=B 或 a=b 时满足题意，此时有： ， ， ， ， = 4。 （方法二） ， 2010 年高考数学试题分类汇编——三角函数 （2010 上海文数）19.（本题满分 12 分） 已知 ，化简： . 解析：原式=lg(sinx+cosx)+lg(cosx+sinx)−lg(sinx+cosx)2=0． （2010 湖南文数）16. （本小题满分 12 分） 已知函数 （I）求函数 的最小正周期。 (II) 求函数 的最大值及 取最大值时 x 的集合。 1cos 3C = 2 1 cos 1tan 2 1 cos 2 C C C −= =+ 2tan 2 2 C = 1tan tan 2 tan 2 A B C = = = tan tan tan tan C C A B + 2 26cos 6 cosb a C ab C a ba b + = ⇒ = + 2 2 2 2 2 2 2 2 36 ,2 2 a b c cab a b a bab + −⋅ = + + = 2tan tan sin cos sin sin cos sin sin( ) 1 sin tan tan cos sin sin cos sin sin cos sin sin C C C B A B A C A B C A B C A B C A B C A B + ++ = ⋅ = ⋅ = ⋅ 0 2x π< < 2lg(cos tan 1 2sin ) lg[ 2 cos( )] lg(1 sin 2 )2 2 xx x x x π⋅ + − + − − + 2( ) sin 2 2sinf x x x= − ( )f x ( )f x ( )f x （2010 浙江理数）（18）(本题满分 l4 分)在△ABC 中,角 A、B、C 所对的边分别为 a,b,c，已知 (I)求 sinC 的值； (Ⅱ)当 a=2， 2sinA=sinC 时，求 b 及 c 的长． 解析：本题主要考察三角变换、正弦定理、余弦定理等基础知识，同事考查运算求解能力。 （Ⅰ）解：因为 cos2C=1-2sin2C= ，及 0＜C＜π 所以 sinC= . （Ⅱ）解：当 a=2，2sinA=sinC 时，由正弦定理 ，得 c=4 由 cos2C=2cos2C-1= ，J 及 0＜C＜π得 cosC=± 由余弦定理 c2=a2+b2-2abcosC，得 b2± b-12=0 解得 b= 或 2 所以 b= b= c=4 或 c=4 （2010 全国卷 2 理数）（17）（本小题满分 10 分） 中， 为边 上的一点， ， ， ，求 ． 【命题意图】本试题主要考查同角三角函数关系、两角和差公式和正弦定理在解三角形中的应用，考查考 生对基础知识、基本技能的掌握情况. 【参考答案】 由 cos∠ADC= ＞0，知 B＜ . 由已知得 cosB= ，sin∠ADC= . 从而 sin∠BAD=sin（∠ADC-B）=sin∠ADCcosB-cos∠ADCsinB= = . ABC∆ D BC 33BD = 5sin 13B = 3cos 5ADC∠ = AD 1cos2 4C = − 1 4 − 10 4 a c sin A sin C = 1 4 − 6 4 6 6 6 6 6 由正弦定理得 ，所以 = . 【点评】三角函数与解三角形的综合性问题，是近几年高考的热点，在高考试题中频繁出现.这类题型难 度比较低，一般出现在 17 或 18 题，属于送分题，估计以后这类题型仍会保留，不会有太大改变.解决此 类问题，要根据已知条件，灵活运用正弦定理或余弦定理，求边角或将边角互化. （2010 陕西文数）17.（本小题满分 12 分） 在△ABC 中，已知 B=45°,D 是 BC 边上的一点， AD=10,AC=14,DC=6，求 AB 的长. 解 在△ADC 中，AD=10,AC=14,DC=6, 由余弦定理得 cos = , ADC=120°, ADB=60° 在△ABD 中，AD=10, B=45°, ADB=60°， 由正弦定理得 , AB= . （2010 辽宁文数）（17）（本小题满分 12 分） 在 中， 分别为内角 的对边， 且 （Ⅰ）求 的大小； （Ⅱ）若 ，试判断 的形状. 解：（Ⅰ）由已知，根据正弦定理得 即 由余弦定理得 故 （Ⅱ）由（Ⅰ）得 又 ，得 ∠ 2 2 2 2 AD DC AC AD DC + −  100 36 196 1 2 10 6 2 + − = −× × ∴ ∠ ∠ ∠ ∠ sin sin AB AD ADB B =∠ ∴ 310sin 10sin 60 2 5 6sin sin 45 2 2 AD ADB B ×∠ °= = =°  ABC∆ a b c、 、 A B C、 、 2 sin (2 )sin (2 )sina A b c B c b C= + + + A sin sin 1B C+ = ABC∆ cbcbcba )2()2(2 2 +++= bccba ++= 222 Abccba cos2222 −+= °=−= 120,2 1cos AA .sinsinsinsinsin 222 CBCBA ++= 1sinsin =+ CB 2 1sinsin == CB 因为 ， 故 所以 是等腰的钝角三角形。 （2010 辽宁理数）（17）（本小题满分 12 分） 在△ABC 中，a, b, c 分别为内角 A, B, C 的对边，且 （Ⅰ）求 A 的大小； （Ⅱ）求 的最大值. 解： （Ⅰ）由已知，根据正弦定理得 即 由余弦定理得 故 ，A=120° ……6 分 （Ⅱ）由（Ⅰ）得： 故当 B=30°时，sinB+sinC 取得最大值 1。 ……12 分 （2010 全国卷 2 文数）（17）（本小题满分 10 分） 中， 为边 上的一点， ， ， ，求 。 【解析】本题考查了同角三角函数的关系、正弦定理与余弦定理的基础知识。 由 与 的差求出 ，根据同角关系及差角公式求出 的正弦，在三角形 ABD 中，由正 弦定理可求得 AD。 （2010 江西理数）17.（本小题满分 12 分） 已知函数 。 (1) 当 m=0 时，求 在区间 上的取值范围； °<<°°<<° 900,900 CB B C= ABC∆ 2 sin (2 )sin (2 )sin .a A a c B c b C= + + + sin sinB C+ 22 (2 ) (2 )a b c b c b c= + + + 2 2 2a b c bc= + + 2 2 2 2 cosa b c bc A= + − 1cos 2A = − sin sin sin sin(60 )B C B B+ = + °− 3 1cos sin2 2 sin(60 ) B B B = + = °+ ABC D BC 33BD = 5sin 13B = 3cos 5ADC∠ = AD ADC∠ B∠ BAD∠ BAD∠ ( ) ( ) 21 cot sin sin sin4 4f x x x m x x π π   = + + + −       ( )f x 3 8 4 π π    ， (2) 当 时， ，求 m 的值。 【解析】考查三角函数的化简、三角函数的图像和性质、已知三角函数值求值问题。依托三角函数化简， 考查函数值域，作为基本的知识交汇问题，考查基本三角函数变换，属于中等题. 解：（1）当 m=0 时， ，由已知 ，得 从而得： 的值域为 （2） 化简得： 当 ，得： ， ， 代入上式，m=-2. （2010 安徽文数）16、（本小题满分 12 分） 的面积是 30，内角 所对边长分别为 ， 。 (Ⅰ)求 ； (Ⅱ)若 ，求 的值。 【命题意图】本题考查同角三角函数的基本关系，三角形面积公式，向量的数量积，利用余弦定理解三角 形以及运算求解能力. 【解题指导】（1）根据同角三角函数关系，由 得 的值，再根据 面积公式得 ；直接求数量积 .由余弦定理 ，代入已知条件 ，及 求 a 的值. 解：由 ，得 . 又 ，∴ . （Ⅰ） . （Ⅱ） ， ∴ . ABC∆ , ,A B C , ,a b c AB AC   a tan 2a = ( ) 3 5f a = 2 2cos 1 cos2 sin 2( ) (1 )sin sin sin cossin 2 x x xf x x x x xx − += + = + = 1[ 2 sin(2 ) 1]2 4x π= − + 3[ , ]8 4x π π∈ 22 [ ,1]4 2x π− ∈ − ( )f x 1 2[0, ]2 + 2cos( ) (1 )sin sin( )sin( )sin 4 4 xf x x m x xx π π= + + + − 1 1( ) [sin 2 (1 )cos2 ]2 2f x x m x= + + + tan 2α = 2 2 2 2sin cos 2tan 4sin 2 sin cos 1 tan 5 a a aa a a a = = =+ + 3cos2 5a = 12cos 13A = 1c b− = 12cos 13A = sin A ABC∆ 156bc = AB AC   2 2 2 2 cosa b c bc A= + − 1c b− = 156bc = 12cos 13A = 212 5sin 1 ( )13 13A = − = 1 sin 302 bc A = 156bc = 12cos 156 14413AB AC bc A⋅ = = × =  2 2 2 2 cosa b c bc A= + − 2 12( ) 2 (1 cos ) 1 2 156 (1 ) 2513c b bc A= − + − = + ⋅ ⋅ − = 5a = 【规律总结】根据本题所给的条件及所要求的结论可知，需求 的值，考虑已知 的面积是 30， ，所以先求 的值，然后根据三角形面积公式得 的值.第二问中求 a 的值，根据第一问 中的结论可知，直接利用余弦定理即可. （2010 重庆文数）(18).(本小题满分 13 分), (Ⅰ)小问 5 分，(Ⅱ)小问 8 分.) 设 的内角 A、B、C 的对边长分别为 a、b、c,且 3 +3 -3 =4 bc . (Ⅰ) 求 sinA 的值； (Ⅱ)求 的值. （2010 浙江文数）（18）（本题满分）在△ABC 中，角 A，B，C 所对的边分别为 a,b,c,设 S 为△ABC 的面积， 满足 。 （Ⅰ）求角 C 的大小； （Ⅱ）求 的最大值。 ABC∆bc 12cos 13A = sin A bc ABC∆ 2b 2c 2a 2 2sin( )sin( )4 4 1 cos2 A B C A π π+ + + − 2 2 23 ( )4S a b c= + − sin sinA B+ （2010 重庆理数）（16）（本小题满分 13 分，（I）小问 7 分，（II）小问 6 分） 设函数 。 （I） 求 的值域； （II） 记 的内角 A、B、C 的对边长分别为 a，b，c，若 =1，b=1,c= ，求 a 的值。 （2010 山东文数）(17)（本小题满分 12 分） ( ) 22cos 2cos ,3 2 xf x x x Rπ = + + ∈   ( )f x ABC∆ ( )f B 3 已知函数 （ ）的最小正周期为 ， （Ⅰ）求 的值； （Ⅱ）将函数 的图像上各点的横坐标缩短到原来的 ，纵坐标不变，得到函数 的图像，求函数 在区间 上的最小值. （2010 北京文数）（15）（本小题共 13 分） 已知函数 （Ⅰ）求 的值； （Ⅱ）求 的最大值和最小值 解：（Ⅰ） = （Ⅱ） 因为 ,所以，当 时 取最大值 2；当 时， 去最小值-1。 （2010 北京理数）（15）（本小题共 13 分）www.@ks@5u.com 已知函数 。 2( ) sin( )cos cosf x x x xπ ω ω ω= − + 0ω > π ω ( )y f x= 1 2 ( )y g x= ( )y g x= 0,16 π     2( ) 2cos2 sinf x x x= + ( )3f π ( )f x 22( ) 2cos sin3 3 3f π π π= + 3 11 4 4 − + = − 2 2( ) 2(2cos 1) (1 cos )f x x x= − + − 23cos 1,x x R= − ∈ [ ]cos 1,1x∈ − cos 1x = ± ( )f x cos 0x = ( )f x (x)f 22cos2 sin 4cosx x x= + − （Ⅰ）求 的值； （Ⅱ）求 的最大值和最小值。 解：（I） （II） = = , 因为 ， 所以，当 时， 取最大值 6；当 时， 取最小值 （2010 四川理数）（19）（本小题满分 12 分） （Ⅰ）○1 证明两角和的余弦公式 ； ○2 由 推导两角和的正弦公式 . （Ⅱ）已知△ABC 的面积 ，且 ，求 cosC. 本小题主要考察两角和的正、余弦公式、诱导公式、同角三角函数间的关系等基础知识及运算能力。 解：(1)①如图，在执教坐标系 xOy 内做单位圆 O，并作出角 α、β 与－β，使角 α 的始边为 Ox，交⊙O 于 点 P1，终边交⊙O 于 P2；角 β 的始边为 OP2，终边交⊙O 于 P3；角－β 的始边为 OP1，终边交⊙O 于 P4. 则 P1(1,0),P2(cosα,sinα) P3(cos(α＋β),sin(α＋β)),P4(cos(－β),sin(－β)) w_w w. k#s5_u.c o*m 由 P1P3＝P2P4 及两点间的距离公式，得 [cos(α＋β)－1]2＋sin2(α＋β)＝[cos(－β)－cosα]2＋[sin(－β)－sinα]2 展开并整理得：2－2cos(α＋β)＝2－2(cosαcosβ－sinαsinβ) ∴cos(α＋β)＝cosαcosβ－sinαsinβ.……………………4 分 ②由①易得 cos( －α)＝sinα,sin( －α)＝cosα sin(α＋β)＝cos[ －(α＋β)]＝cos[( －α)＋(－β)] ＝cos( －α)cos(－β)－sin( －α)sin(－β) ＝sinαcosβ＋cosαsinβ……………………………………6 分 (2)由题意，设△ABC 的角 B、C 的对边分别为 b、c 则 S＝ bcsinA＝ ＝bccosA＝3＞0w_w w. k#s5_u.c o*m ( )3f π= (x)f 22 3 9( ) 2cos sin 4cos 13 3 3 3 4 4f π π π π= + − = − + = − 2 2( ) 2(2cos 1) (1 cos ) 4cosf x x x x= − + − − 23cos 4cos 1x x− − 22 73(cos )3 3x − − x R∈ cos x ∈ [ 1,1]− cos 1x = − ( )f x 2cos 3x = ( )f x 7 3 − C : cos( ) cos cos sin sinα β α β α β α β+ + = − Cα β+ S : sin( ) sin cos cos sinα β α β α β α β+ + = + 1 , 32S AB AC= • =  3 5cos B = 2 π 2 π 2 π 2 π 2 π 2 π 1 2 1 2 AB AC•  ∴A∈(0, ),cosA＝3sinA 又 sin2A＋cos2A＝1，∴sinA＝ ,cosA＝ 由题意，cosB＝ ,得 sinB＝ ∴cos(A＋B)＝cosAcosB－sinAsinB＝ w_w w. k#s5_u.c o*m 故 cosC＝cos[π－(A＋B)]＝－cos(A＋B)＝－ …………………………12 分 （2010 天津文数）（17）（本小题满分 12 分） 在 ABC 中， 。 （Ⅰ）证明 B=C： （Ⅱ）若 =- ，求 sin 的值。 【解析】本小题主要考查正弦定理、两角和与差的正弦、同角三角函数的基本关系、二倍角的正弦与余弦 等基础知识，考查基本运算能力.满分 12 分. （Ⅰ）证明：在△ABC 中，由正弦定理及已知得 = .于是 sinBcosC-cosBsinC=0，即 sin （B-C）=0.因为 ，从而 B-C=0. 所以 B=C. （Ⅱ）解：由 A+B+C= 和（Ⅰ）得 A= -2B,故 cos2B=-cos（ -2B）=-cosA= . 又 0<2B< ,于是 sin2B= = . 从而 sin4B=2sin2Bcos2B= ，cos4B= . 所以 （2010 天津理数）（17）（本小题满分 12 分） 已知函数 2 π 10 10 3 10 10 3 5 4 5 10 10 10 10 ∆ cos cos AC B AB C = cos A 1 3 4B 3 π +   sin B sin C cosB cosC B Cπ π− < − < π π π 1 3 π 21 cos 2B− 2 2 3 4 2 9 2 2 7cos 2 sin 2 9B B− = − 4 2 7 3sin(4 ) sin 4 cos cos4 sin3 3 3 18B B B π π π −+ = + = 2( ) 2 3sin cos 2cos 1( )f x x x x x R= + − ∈ （Ⅰ）求函数 的最小正周期及在区间 上的最大值和最小值； （Ⅱ）若 ，求 的值。 【解析】本小题主要考查二倍角的正弦与余弦、两角和的正弦、函数 的性质、同角三角 函数的基本关系、两角差的余弦等基础知识，考查基本运算能力，满分 12 分。 （1）解：由 ，得 所以函数 的最小正周期为 因为 在区间 上为增函数，在区间 上为减函数，又 ，所以函数 在区间 上的最大值为 2，最小值为-1 （Ⅱ）解：由（1）可知 又因为 ，所以 由 ，得 从而 所以 （2010 广东理数）16、（本小题满分 14 分） 已知函数 在 时取得最大值 4．　 (1) 求 的最小正周期； ( )f x 0, 2 π     0 0 6( ) , ,5 4 2f x x π π = ∈   0cos2x sin( )y A xω ϕ= + 2( ) 2 3sin cos 2cos 1f x x x x= + − 2( ) 3(2sin cos ) (2cos 1) 3sin 2 cos2 2sin(2 )6f x x x x x x x π= + − = + = + ( )f x π ( ) 2sin 2 6f x x π = +   0, 6 π     ,6 2 π π     (0) 1, 2, 16 2f f f π π   = = = −       ( )f x 0, 2 π     0 0( ) 2sin 2 6f x x π = +   0 6( ) 5f x = 0 3sin 2 6 5x π + =   0 ,4 2x π π ∈   0 2 72 ,6 3 6x π π π + ∈   2 0 0 4cos 2 1 sin 26 6 5x x π π   + = − − + = −       0 0 0 0 3 4 3cos2 cos 2 cos 2 cos sin 2 sin6 6 6 6 6 6 10x x x x π π π π π π  −     = + − = + + + =             ( ) sin(3 )( 0, ( , ),0f x A x A xϕ ϕ π= + > ∈ −∞ +∞ < < 12x π= ( )f x (2) 求 的解析式； (3) 若 ( α + )= ,求 sinα．[来源:高考资源网 KS5U.COM] ， ， ， ， ．[来 （2010 广东文数） （2010 全国卷 1 理数）(17)(本小题满分 10 分) ( )f x f 2 3 12 π 12 5 3sin(2 )2 5 πα + = 3cos2 5 α = 2 31 2sin 5 α− = 2 1sin 5 α = 5sin 5 α = ± 已知 的内角 ， 及其对边 ， 满足 ，求内角 ． （2010 四川文数）（19）（本小题满分 12 分）w_w w. k#s5_u.c o* （Ⅰ）○1 证明两角和的余弦公式 ； ○2 由 推导两角和的正弦公式 . （Ⅱ）已知 ，求 （2010 湖北文数）16.（本小题满分 12 分） 已经函数 (Ⅰ)函数 的图象可由函数 的图象经过怎样变化得出？ ABC A B a b cot cota b a A b B+ = + C C : cos( ) cos cos sin sinα β α β α β α β+ + = − Cα β+ S : sin( ) sin cos cos sinα β α β α β α β+ + = + 4 3 1cos , ( , ),tan , ( , ),cos( )5 2 3 2 πα α π π β β π α β= − ∈ = − ∈ + cos( )α β+ 2 2cos sin 1 1( ) , ( ) sin 2 .2 2 4 x xf x g x x −= = − ( )f x ( )g x （Ⅱ）求函数 的最小值，并求使用 取得最小值的 的集合。 （2010 山东理数） ( ) ( ) ( )h x f x g x= − ( )h x x （2010 湖南理数）16．（本小题满分 12 分） 已知函数 ． （Ⅰ）求函数 的最大值； （II）求函数 的零点的集合。 （2010 湖北理数） 16．（本小题满分 12 分） 已知函数 f(x)= （Ⅰ）求函数 f(x)的最小正周期； （Ⅱ）求函数 h（x）=f(x)－g(x)的最大值，并求使 h(x)取得最大值的 x 的集合。 2( ) 3sin 2 2sinf x x x= − ( )f x ( )f x 1 1cos( )cos( ), ( ) sin 23 3 2 4x x g x x π π+ − = − （2010 福建理数）19．（本小题满分 13 分） 。 ，轮船位于港口 O 北偏西 且与该港口相距 20 海里的 A 处，并以 30 海里/小时的航行速度沿正东方向匀速行驶。假设该 小船沿直线方向以 海里/小时的航行速度匀速行驶，经过 t 小时与轮船相遇。 （1）若希望相遇时小艇的航行距离最小，则小艇航行速度的大小应为多少？ （2）假设小艇的最高航行速度只能达到 30 海里/小时，试设计航行方案（即确定航行方向与航行速度的 大小），使得小艇能以最短时间与轮船相遇，并说明理由。 【解析】如图，由（1）得 而小艇的最高航行速度只 能 达 到 30 海 里 / 小 时 ， 故 轮 船 与 小 艇 不 可 能 在 A 、 C （ 包 含 C ） 的 任 意 位 置 相 遇 ， 设 ，OD= ， 由于从出发到相遇，轮船与小艇所需要的时间分别为 和 ， 所以 ，解得 ， 从而 值，且最小值为 ，于是 当 取得最小值，且最小值为 。 此时，在 中， ，故可设计航行方案如下： 航行方向为北偏东 ，航行速度为 30 海里/小时，小艇能以最短时间与轮船相遇。 O某港口 要将一件重要物品用小艇送到一艘正在航行的轮船上 在小艇出发时 30 v 10 3,AC=10, > , , >ACOC OC AC AC= ≥故 且对于线段 上任意点P有OP OC ， COD= (0 < <90 ), 10 3 tanRt COD CDθ θ θ∠ ∆ =  则在 中， 10 3 cosθ 10 10 3 tan 30t θ+= 10 3 cost v θ= 10 10 3 tan 30 θ+ 10 3 cosv θ= 15 3 3, 30, sin ( +30 )sin ( +30 ) 2v v θθ= ≤ ≥  又 故 30 <90 , 30 tanθ θ θ≤ =  由于 时， 取得最小 3 3 30θ = 时， 10 10 3 tan 30t θ+= 2 3 OAB∆ 20OA OB AB= = = 30 （2010 安徽理数）16、（本小题满分 12 分） 设 是锐角三角形， 分别是内角 所对边长，并且 。 (Ⅰ)求角 的值； (Ⅱ)若 ，求 （其中 ）。 （2010 江苏卷）17、（本小题满分 14 分） 某兴趣小组测量电视塔 AE 的高度 H(单位：m），如示意图，垂直放置的标杆 BC 的高度 h=4m，仰角∠ABE= ，∠ADE= 。 (1)该小组已经测得一组 、 的值，tan =1.24，tan =1.20，请据此算出 H 的值； (2)该小组分析若干测得的数据后，认为适当调整标杆到电视塔的距离 d（单位：m），使 与 之差较大，可以提高测量精确度。若电视塔的 实际高度为 125m，试问 d 为多少时， - 最大？ [解析] 本题主要考查解三角形的知识、两角差的正切及不等式的应用。 ABC∆ , ,a b c , ,A B C 2 2sin sin( ) sin( ) sin3 3A B B B π π= + − + A 12, 2 7AB AC a= =   ,b c b c< α β α β α β α β α β （1 ） ，同理： ， 。 AD—AB=DB，故得 ，解得： 。 因此，算出的电视塔的高度 H 是 124m。 （2）由题设知 ，得 ， ，（当且仅当 时，取等号） 故当 时， 最大。 因为 ，则 ，所以当 时， - 最大。 故所求的 是 m。 （2010 江苏卷）23.（本小题满分 10 分） 已知△ABC 的三边长都是有理数。 （1）求证 cosA 是有理数；（2）求证：对任意正整数 n，cosnA 是有理数。 [解析] 本题主要考查余弦定理、数学归纳法等基础知识，考查推理论证的能力与分析问题、解决问题的能 力。满分 10 分。 （方法一）（1）证明：设三边长分别为 ， ，∵ 是有理数， 是有理数，分母 为正有理数，又有理数集对于除法的具有封闭性， ∴ 必为有理数，∴cosA 是有理数。 （2）①当 时，显然 cosA 是有理数； 当 时，∵ ，因为 cosA 是有理数， ∴ 也是有理数； ②假设当 时，结论成立，即 coskA、 均是有理数。 当 时， ， ， tan tan H HADAD β β= ⇒ = tan HAB α= tan hBD β= tan tan tan H H h β α β− = tan 4 1.24 124tan tan 1.24 1.20 hH α β α ×= = =− − d AB= tan ,tanH H h H h d AD DB d α β −= = = = 2 tan tantan( ) ( )1 tan tan ( )1 H H h hd hd d H H h H H hd H H h dd d d α βα β α β −−−− = = = =− −+ ⋅ + −+ ⋅ + ( ) 2 ( )H H hd H H hd −+ ≥ − ( ) 125 121 55 5d H H h= − = × = 55 5d = tan( )α β− 0 2 πβ α< < < 0 2 πα β< − < 55 5d = α β d 55 5 , ,a b c 2 2 2 cos 2 b c aA bc + −= , ,a b c 2 2 2b c a+ − 2bc 2 2 2 2 b c a bc + − 1n = 2n = 2cos2 2cos 1A A= − cos2A ( 2)n k k≤ ≥ cos( 1)k A− 1n k= + cos( 1) cos cos sin sink A kA A kA A+ = − 1cos( 1) cos cos [cos( ) cos( )]2k A kA A kA A kA A+ = − − − + ， 解得： ∵cosA， ， 均是有理数，∴ 是有理数， ∴ 是有理数。 即当 时，结论成立。 综上所述，对于任意正整数 n，cosnA 是有理数。 （方法二）证明：（1）由 AB、BC、AC 为有理数及余弦定理知 是有理数。 （2）用数学归纳法证明 cosnA 和 都是有理数。 ①当 时，由（1）知 是有理数，从而有 也是有理数。 ②假设当 时， 和 都是有理数。 当 时，由 ， ， 及①和归纳假设，知 和 都是有理数。 即当 时，结论成立。 综合①、②可知，对任意正整数 n，cosnA 是有理数。 1 1cos( 1) cos cos cos( 1) cos( 1)2 2k A kA A k A k A+ = − − + + cos( 1) 2cos cos cos( 1)k A kA A k A+ = − − coskA cos( 1)k A− 2cos cos cos( 1)kA A k A− − cos( 1)k A+ 1n k= + 2 2 2 cos 2 AB AC BCA AB AC + −= ⋅ sin sinA nA⋅ 1n = cos A 2sin sin 1 cosA A A⋅ = − ( 1)n k k= ≥ coskA sin sinA kA⋅ 1n k= + cos( 1) cos cos sin sink A A kA A kA+ = ⋅ − ⋅ sin sin( 1) sin (sin cos cos sin ) (sin sin ) cos (sin sin ) cosA k A A A kA A kA A A kA A kA A⋅ + = ⋅ ⋅ + ⋅ = ⋅ ⋅ + ⋅ ⋅ cos( 1)k A+ sin sin( 1)A k A⋅ + 1n k= +