最后十套高考名校考前提分仿真卷 理科数学八带答案 11页

绝密 ★ 启用前 ‎【最后十套】2019届高考名校考前提分仿真卷 理 科 数 学（八）‎ 注意事项：‎ ‎1、本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。答题前，考生务必将自己的姓名、考生号填写在答题卡上。‎ ‎2、回答第Ⅰ卷时，选出每小题的答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号。写在试卷上无效。‎ ‎3、回答第Ⅱ卷时，将答案填写在答题卡上，写在试卷上无效。‎ ‎4、考试结束，将本试卷和答题卡一并交回。‎ 第Ⅰ卷 一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．[2019·淮南一模]（ ）‎ A． B． C． D．‎ ‎2．[2019·九狮联盟]已知集合，，则（ ）‎ A． B． C． D．‎ ‎3．[2019·日照一模]函数的图象大致为（ ）‎ A． B．‎ C． D．‎ ‎4．[2019·邢台二中]已知向量，，若，则（ ）‎ A． B．0 C．1 D．2‎ ‎5．[2019·重庆一中]2018年，国际权威机构IDC发布的全球手机销售报告显示：华为突破2亿台出货量超越苹果的出货量，首次成为全球第二，华为无愧于中国最强的高科技企业。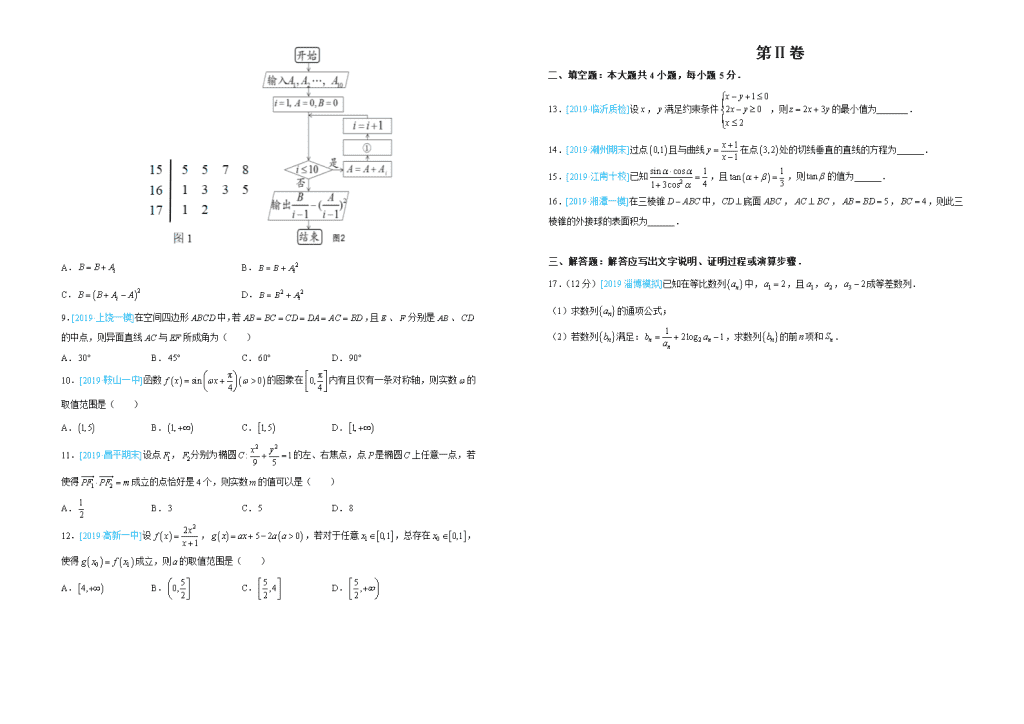华为业务CEO余承东明确表示，华为的目标，就是在2021年前，成为全球最大的手机厂商．为了解华为手机和苹果手机使用的情况是否和消费者的性别有关，对100名华为手机使用者和苹果手机使用者进行统计，统计结果如下表：‎ 根据表格判断是否有的把握认为使用哪种品牌手机与性别有关系，则下列结论正确的是（ ）‎ 附：．‎ A．没有把握认为使用哪款手机与性别有关 B．有把握认为使用哪款手机与性别有关 C．有把握认为使用哪款手机与性别无关 D．以上都不对 ‎6．[2019·东师附中]已知双曲线的右焦点到渐近线的距离等于实轴长，则此双曲线的离心率为（ ）‎ A． B． C． D．‎ ‎7．[2019·江南十校]在中，角、、的对边分别为、、，若，，，则的值为（ ）‎ A． B． C． D．‎ ‎8．[2019·南昌模拟]根据某校10位高一同学的身高(单位：cm)画出的茎叶图（图1），其中左边的数字从左到右分别表示学生身高的百位数字和十位数字，右边的数字表示学生身高的个位数字，设计一个程序框图（图2），用表示第个同学的身高，计算这些同学身高的方差，则程序框图①中要补充的语句是（ ）‎ A． B．‎ C． D．‎ ‎9．[2019·上饶一模]在空间四边形中，若，且、分别是、的中点，则异面直线与所成角为（ ）‎ A． B． C． D．‎ ‎10．[2019·鞍山一中]函数的图象在内有且仅有一条对称轴，则实数的取值范围是（ ）‎ A． B． C． D．‎ ‎11．[2019·昌平期末]设点，分别为椭圆的左、右焦点，点是椭圆上任意一点，若使得成立的点恰好是个，则实数的值可以是（ ）‎ A． B． C． D．‎ ‎12．[2019·高新一中]设，，若对于任意，总存在，使得成立，则的取值范围是（ ）‎ A． B． C． D．‎ 第Ⅱ卷 二、填空题：本大题共4小题，每小题5分．‎ ‎13．[2019·临沂质检]设，满足约束条件，则的最小值为_______．‎ ‎14．[2019·潮州期末]过点且与曲线在点处的切线垂直的直线的方程为______．‎ ‎15．[2019·江南十校]已知，且，则的值为______．‎ ‎16．[2019·湘潭一模]在三棱锥中，底面，，，，则此三棱锥的外接球的表面积为______．‎ 三、解答题：解答应写出文字说明、证明过程或演算步骤．‎ ‎17．（12分）[2019淄博模拟]已知在等比数列中，，且，，成等差数列．‎ ‎（1）求数列的通项公式；‎ ‎（2）若数列满足：，求数列的前项和．‎ ‎18．（12分）[2019·汕头一模]我市南澳县是广东唯一的海岛县，海区面积广阔，发展太平洋牡蛎养殖业具有得天独厚的优势，所产的“南澳牡蛎”是中国国家地理标志产品，产量高、肉质肥、营养好，素有“海洋牛奶精品”的美誉．根据养殖规模与以往的养殖经验，产自某南澳牡蛎养殖基地的单个“南澳牡蛎”质量（克）在正常环境下服从正态分布．‎ ‎（1）购买10只该基地的“南澳牡蛎”，会买到质量小于的牡蛎的可能性有多大？‎ ‎（2）2019年该基地考虑增加人工投入，现有以往的人工投入增量（人）与年收益增量（万元）的数据如下：‎ 人工投入增量（人）‎ ‎2‎ ‎3‎ ‎4‎ ‎6‎ ‎8‎ ‎10‎ ‎13‎ 年收益增量（万元）‎ ‎13‎ ‎22‎ ‎31‎ ‎42‎ ‎50‎ ‎56‎ ‎58‎ 该基地为了预测人工投入增量为16人时的年收益增量，建立了与的两个回归模型：‎ 模型①：由最小二乘公式可求得与的线性回归方程：；‎ 模型②：由散点图的样本点分布，可以认为样本点集中在曲线：的附近，对人工投入增量做变换，令，则，且有，，，．‎ ‎（i）根据所给的统计量，求模型②中关于的回归方程（精确到）；‎ ‎（ii）根据下列表格中的数据，比较两种模型的相关指数，并选择拟合精度更高、更可靠的模型，预测人工投入增量为16人时的年收益增量．‎ 回归模型 模型①‎ 模型②‎ 回归方程 附：若随机变量，则，；‎ 样本的最小二乘估计公式为：，，‎ 另，刻画回归效果的相关指数．‎ ‎19．（12分）[2019·哈尔滨三中]如图所示，在四棱台中，底面，四边形为菱形，，．‎ ‎（1）若为中点，求证：平面；‎ ‎（2）求直线与平面所成角的正弦值．‎ ‎20．（12分）[2019·扬州一模]已知直线上有一动点，过点作直线垂直于轴，动点在上，且满足（为坐标原点），记点的轨迹为曲线．‎ ‎（1）求曲线的方程；‎ ‎（2）已知定点，，为曲线上一点，直线交曲线于另一点，且点在线段上，直线交曲线于另一点，求的内切圆半径的取值范围．‎ ‎21．（12分）[2019·荆州中学]设，．‎ ‎（1）求的单调区间；‎ ‎（2）讨论零点的个数；‎ ‎（3）当时，设恒成立，求实数的取值范围．‎ 请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分．‎ ‎22．（10分）【选修4-4：坐标系与参数方程】‎ ‎[2019·临淄模拟]在平面直角坐标系中，直线的参数方程为（为参数，）．以坐标原点为极点，轴正半轴为极轴建立极坐标系，曲线的极坐标方程为．‎ ‎（1）写出曲线的直角坐标方程；‎ ‎（2）若直线与曲线交于，两点，且的长度为，求直线的普通方程．‎ ‎23．（10分）【选修4-5：不等式选讲】‎ ‎[2019·太原期末]已知函数，．‎ ‎（1）当时，解不等式；‎ ‎（2）若不等式对任意恒成立，求实数的取值范围．‎ 绝密 ★ 启用前 ‎【最后十套】2019届高考名校考前提分仿真卷 理科数学答案（八）‎ 第Ⅰ卷 一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．【答案】C ‎【解析】，故选C．‎ ‎2．【答案】C ‎【解析】∵，解得，∴，‎ 又∵，∴．故选C．‎ ‎3．【答案】A ‎【解析】函数是偶函数，排除选项B、C，‎ 当时，，时，函数是增函数，排除D．故选A．‎ ‎4．【答案】C ‎【解析】∵，∴，得，∴．故选C．‎ ‎5．【答案】A ‎【解析】由表可知：，，，，，‎ 则，‎ 故没有把握认为使用哪款手机与性别有关，故选A．‎ ‎6．【答案】C ‎【解析】由题意可设双曲线的右焦点，渐进线的方程为，‎ 可得，可得，可得离心率，故选C．‎ ‎7．【答案】B ‎【解析】由正弦定理可得：，‎ 即，‎ ‎∴，故选B．‎ ‎8．【答案】B ‎【解析】由 ‎，‎ 循环退出时，知．∴，‎ 故程序框图①中要补充的语句是．故选B．‎ ‎9．【答案】B ‎【解析】在图1中连接，，‎ ‎∵，得为等腰三角形，‎ 设空间四边形的边长为2，即，‎ 在中，，，得．‎ ‎ ‎ 图1 图2‎ 在图2取的中点，连接、，∵、分别是、的中点，‎ ‎∴，，是异面直线与所成的角．‎ 在中可由余弦定理得，‎ ‎∴，即异面直线所成的角为．故选B．‎ ‎10．【答案】C ‎【解析】当时，，当，，‎ ‎∵在只有一条对称轴，可知，解得，故选C．‎ ‎11．【答案】B ‎【解析】∵点，分别为椭圆的左、右焦点；‎ 即，，，，，，‎ 设，，，‎ 由可得，‎ 又∵在椭圆上，即，∴，‎ ‎ 要使得成立的点恰好是个，则，解得，‎ ‎∴的值可以是3．故选B．‎ ‎12．【答案】C ‎【解析】∵，∴当时，，当时，，‎ 由，∴，故，‎ 又∵，且，．故．‎ ‎∵对于任意，总存在，使得成立，‎ ‎∴在的值域是在的值域的子集，∴须满足，‎ ‎∴，的取值范围是，故选C．‎ 第Ⅱ卷 二、填空题：本大题共4小题，每小题5分．‎ ‎13．【答案】8‎ ‎【解析】画出不等式组表示的平面区域，如图阴影部分所示，‎ 由图形知，当目标函数过点时，取得最小值；‎ 由，求得；∴的最小值是．故答案为8．‎ ‎14．【答案】‎ ‎【解析】∵，∴，‎ 当时，，即曲线在点处的切线斜率为，‎ ‎∴与曲线在点处的切线垂直的直线的斜率为2，‎ ‎∵直线过点，∴所求直线方程为，即．故答案为．‎ ‎15．【答案】‎ ‎【解析】∵，∴，‎ 又，解得．故答案为．‎ ‎16．【答案】‎ ‎【解析】由题意，在三棱锥中，底面，，，，‎ 可得，‎ 故三棱锥的外接球的半径，则其表面积为．‎ 三、解答题：解答应写出文字说明、证明过程或演算步骤．‎ ‎17．【答案】（1）；（2）．‎ ‎【解析】（1）设等比数列的公比为，‎ ‎∵，，成等差数列，∴，‎ ‎∴．‎ ‎（2）∵，‎ ‎∴‎ ‎．‎ ‎18．【答案】（1）；（2）（i），（ii）见解析．‎ ‎【解析】（1）由已知，单个“南澳牡蛎”质量，则，，‎ 由正态分布的对称性可知，‎ ‎，‎ ‎ 设购买10只该基地的“南澳牡蛎”，其中质量小于的牡蛎为只，故，故，‎ ‎∴这10只“南澳牡蛎”中，会买到质量小于20g的牡蛎的可能性仅为． ‎ ‎（2）（i）由，，，，‎ 有，且，‎ ‎∴模型②中关于的回归方程为．‎ ‎（ii）由表格中的数据，有，即模型①的小于模型②，说明回归模型②刻画的拟合效果更好．‎ 当时，模型②的收益增量的预测值为（万元），‎ 这个结果比模型①的预测精度更高、更可靠．‎ ‎19．【答案】（1）见解析；（2）．‎ ‎【解析】（1）∵四边形为菱形，，连结，则为等边三角形，‎ 又∵为中点，∴，由，∴，‎ ‎∵底面，底面，∴，‎ 又∵，∴平面．‎ ‎（2）∵四边形为菱形，，，‎ ‎∴，，∴，‎ 又∵底面，‎ 分别以，，为轴、轴、轴，建立如图所示的空间直角坐标系，‎ ‎、、、，‎ ‎∴，，，‎ 设平面的一个法向量，‎ 则有，令，则，‎ ‎∴直线与平面所成角的正弦值．‎ ‎20．【答案】（1）；（2）．‎ ‎【解析】（1）设点，则，∴，．‎ ‎∵，∴，即．‎ ‎（2）设，，，直线与轴交点为，直线与内切圆的切点为．‎ 设直线的方程为，则联立方程组得，‎ ‎∴且，∴，∴直线的方程为，‎ 与方程联立得，‎ 化简得，解得或．‎ ‎∵，∴轴，‎ 设的内切圆圆心为，则点在轴上且．‎ ‎∴，且的周长，‎ ‎∴，‎ ‎∴，‎ 令，则，∴在区间上单调递增，‎ 则，即的取值范围为．‎ ‎21．【答案】（1）的单调递增区间为，单调递减区间为；（2）见解析；（3）．‎ ‎【解析】（1），‎ 当时，，递增，当时，，递减，‎ 故的单调递增区间为，单调递减区间为．‎ ‎（2）是的一个零点，当时，由得，，，‎ 当时，递减且，‎ 当时，，且时，递减，‎ 当时，递增，故，‎ 大致图像如图，‎ ‎∴当时，有1个零点；当或时，有2个零点；‎ 当时，有3个零点． ‎ ‎（3），‎ ‎，，‎ 设的根为，即有，可得，‎ 当时，，递减，当时，，递增，‎ ‎，‎ ‎∴．‎ 请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分．‎ ‎22．【答案】（1）；（2）和．‎ ‎【解析】（1）将代入曲线极坐标方程得：‎ 曲线的直角坐标方程为，即．‎ ‎（2）将直线的参数方程代入曲线方程：，‎ 整理得，‎ 设点，对应的参数为，，解得，，‎ 则，‎ ‎∵，∴和，∴直线的普通方程为和．‎ ‎23．【答案】（1）；（2）．‎ ‎【解析】（1）当时，，∴，‎ 即求不同区间对应解集，∴的解集为．‎ ‎（2）由题意，对任意的恒成立，‎ 即对任意的恒成立，‎ 令，‎ ‎∴函数的图象应该恒在的下方，数形结合可得．‎